水利工程中,库区边坡坍塌滑移会引发水库涌浪,威胁大坝安全,造成严重工程事故。库区边坡的稳定性对大坝安全具有重要意义,在大坝建设过程中,探明坝址区边坡的地质条件十分必要。在西南水电工程开发过程中,研究者发现西南深切河谷具有高地应力、边坡失稳等问题;在苗家坝、向家坝、白鹤滩等[1-6]实际工程实践中,发现岸坡发育有深部裂缝,并具有深度大、分布范围广等特点。深部裂缝影响工程建设和边坡安全,因此研究深部裂缝的成因及对坡变形的影响具有重要意义。
锦屏一级水电站位于四川省凉山彝族自治州境内,最大坝高为305 m,运行近10年的监测资料显示,锦屏左岸边坡高高程临空向变形仍在发展[7-8]。锦屏河谷为典型的西南深切V形河谷[9-12],锦屏左岸边坡分布有诸多深部裂缝,这些深部裂缝一直是学术研究和工程关注的热点。部分学者对深部裂缝的成因进行了研究,研究内容大致分为以下2类。
工程地质方面:祁生文等[13]通过分析锦屏左岸深部裂缝的分布特征和早期地质构造作用,认为锦屏左岸深部裂缝的形成和分布与岩性、坡岸结构、地形、以往构造活动和现代水平构造应力场强度等因素有关;同时从工程类比角度探讨了锦屏左岸深部裂缝的成因[14],通过对比锦屏左岸与锦屏右岸、锦屏右岸与三滩右岸、锦屏左岸与三滩左岸,表明河谷下切、地壳上升和高地应力是深部裂缝发育的必要条件,而非充分条件。
数值模拟方面:荣冠等[15]通过离散元法模拟锦屏河谷演化发展过程,认为锦屏左岸深部裂缝是在河谷上软下硬、反倾向边坡、河谷下切迅速和高地应力等特定条件下,在河谷下切至对应高程时出现局部应力集中,导致边坡岩体局部应力超过其承载力而屈服破坏的结果;徐佩华等[16]对锦屏一级水电站坝址区进行了数值模拟分析,结果表明,锦屏河谷应力场应力分异现象显著,左岸边坡受煌斑岩脉和断层影响,卸荷深度显著加大。
现有研究对深部裂缝的成因已有一定认识[17-21],但存在所建模型精细度低、对形成深部裂缝的力学机制认识不足等问题,使分析工程地质得出的结论未体现在数值模拟中。本文基于地应力演化数值模拟,研究深部裂缝成因及对边坡变形的影响,为分析锦屏左岸边坡运行期持续变形机制、整体稳定性等奠定基础。本文首先建立锦屏坝址区三维模型,采用有限元法模拟分析河谷下切不同阶段对边坡地应力的影响;其次,结合数值模拟和工程地质分析结果,总结影响边坡深卸荷的因素,并通过分析主应力随河谷下切过程的变化特征,探究1930、1780 m高程形成深部裂缝的力学机制;最后,通过分析变形监测资料和边坡岩体蠕变计算,研究锦屏左岸深部裂缝对边坡运行期变形的影响。
1 地质条件锦屏左岸边坡工程规模较大,坝址区自然边坡高度超过1 500 m,工程边坡高度达530 m,总开挖量约550×104 m3。坝址区自然边坡地质条件复杂,为典型的深切V形河谷反倾向边坡,坡度为40°~50°,相对高差上千米。海拔约1 820 m以上的地层主要为砂板岩,1 820 m以下为大理岩。锦屏左岸边坡主要地质构造特征如表 1[22]所示,岩体中有诸多不良地质构造,如煌斑岩脉X,断层f2、f5、f8、f42-9,以及一系列规模不等的张开裂缝和深部裂缝等,这些构造使锦屏左岸上部形成深度较大的Ⅳ2类岩体,岩体刚度明显低于右岸。锦屏左岸边坡的深部裂缝大致分为2类:一类是边坡卸荷深度远超以往工程实践,从边坡表层至深部200~300 m均有裂缝发育,因卸荷深度大,所以称为深卸荷,其中1 930 m高程最为典型,如图 1a所示;另一类是在边坡浅表层卸荷带和相对完整的岩体后,边坡岩体深部300 m左右出现的卸荷裂缝,称为深拉裂缝,深拉裂缝主要集中在1 780 m高程,如图 1b所示。
| 主要结构面 | 总体产状 | 厚度/m | 岩性组成 | 分布高程/m |
| 断层f2 | N20°~30°E/ NW∠30°~50° | 0.1~0.8 | 以岩屑夹泥型为主 | 1 500~1 700 |
| 断层f5 | N35°~55°E/ SE∠65°~80° | 5.0~10.0(砂板岩段) 1.0~3.0(大理岩段) | 由黑色糜棱岩、角砾岩和连续断层泥组成 | 贯穿左岸,顶高程至2 000 |
| 断层f8 | N20°~60°E/ SE∠60°~70° | 1.0~2.0(1 935 m高程及以上) 0.3~0.5(1 935 m高程以下) | 由黄褐色碎裂岩、角砾岩和不连续断层泥组成 | 1 750~1 950 |
| 断层f42-9 | N80°E~近EW/ SE(S)∠40°~55° | 0.2~1.3 | 由糜棱岩和少量断层泥组成 | 1 800~1 980 |
| 煌斑岩脉X | N60°~80°E/ SE∠70°~90° | 2.0~4.0 | 以弱风化岩体为主,局部为强风化岩体 | 贯穿左岸,顶高程至2 060 |
| 松弛拉裂带SL44-1 | SN~N20°W/ NE∠55°~60° | 0.1~0.5 | 由岩块、岩屑和片状岩组成,强风化 | 1 750~2 080 |
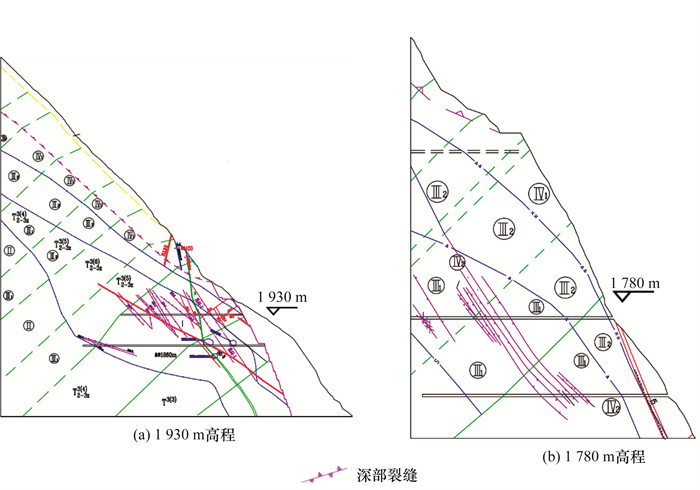
|
| 图 1 锦屏左岸边坡深部裂缝分布图 |
水平方向上,深部裂缝的分布与f5、f8等断层大致平行,越向上游深部裂缝埋深越大;垂直方向上,深部裂缝的分布具有明显差异性,主要分布在1 780~1 930 m高程,1 700 m高程以下极少[23]。
2 河谷演化数值模拟 2.1 计算模型本文所建模型模拟范围为2 000 m×2 740 m× 1 600 m。顺河向:上游至距离坝轴线约1 540 m的解放沟坝址勘探线;下游至距离坝轴线约800 m的二道坝坝轴线。横河向:左岸距坝体中心点1 230 m;右岸据坝体中心点1 100 m。高程方向:海拔1 100~ 2 700 m (河谷底部高程1 100 m,拱坝顶部高程1 885 m)。网格节点总数为122 783个,单元总数为115 307个。该模型模拟了煌斑岩脉X和断层fw、f5、f8等,如图 2所示。
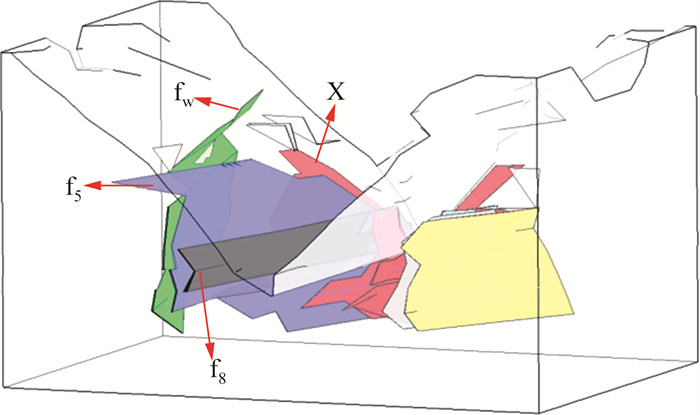
|
| 图 2 软弱带模拟示意图 |
2.2 河谷下切模拟
模拟河谷从平坦地面下切至现在形状,即从2 400 m高程下切至现在河床高程1 600 m,分5级下切,如表 2所示。由于河谷下切年代久远,难以确定各级下切过程的岸坡线。因此,根据河谷两岸不对称特点,结合现在坡岸线确定下切过程的河谷轮廓线,如图 3所示。
| m | |||||||||||||||||||||||||||||
| 下切次序 | 下切高程 | 下切深度 | |||||||||||||||||||||||||||
| 1级下切 | 2 200~2 400 | 200 | |||||||||||||||||||||||||||
| 2级下切 | 2 100~2 200 | 100 | |||||||||||||||||||||||||||
| 3级下切 | 2 000~2 100 | 100 | |||||||||||||||||||||||||||
| 4级下切 | 1 800~2 000 | 200 | |||||||||||||||||||||||||||
| 5级下切 | 1 600~1 800 | 200 | |||||||||||||||||||||||||||
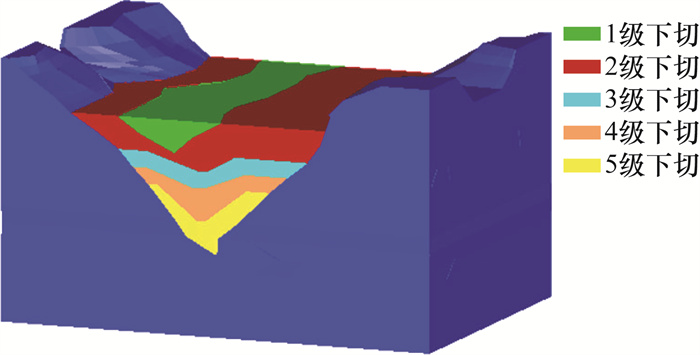
|
| 图 3 河谷下切过程示意图 |
2.3 计算工况和过程
文[16]根据实测地应力资料,分析了锦屏河谷构造应力的大小,采用横河向施加对称12 MPa、顺河向施加对称8 MPa平面应力的方式模拟构造应力。本文结合所建模型情况,采取的边界条件分为2种工况,如图 4所示。
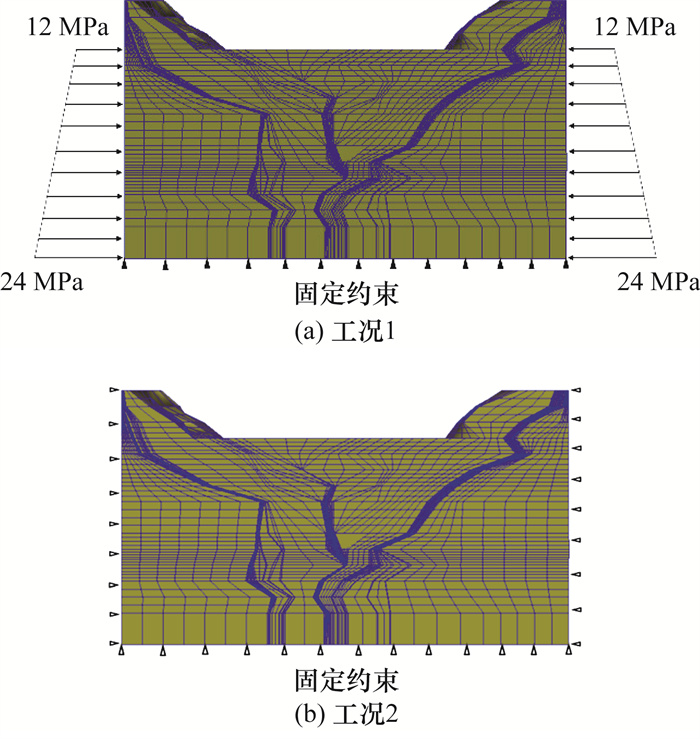
|
| 图 4 不同工况下边界条件 |
工况1:下切过程考虑重力和构造应力作用,模型底部采用位移约束,约束顺河向x、横河向y和竖直向z位移。模型四周1 100~2 400 m高程(下切河谷对应部分)施加顶部12 MPa、底部24 MPa的对称梯形荷载,模拟构造应力。
工况2:下切过程仅考虑重力作用,不施加构造应力,模型底部约束竖直向位移,模型四周约束法向位移,即横河向模型表面约束横河向位移,顺河向模型表面约束顺河向位移。
计算过程如下:
1) 采用弹塑性模型进行河谷下切数值计算,分5级开挖模拟河谷下切。
2) 采用蠕变损伤模型进行蠕变计算,求解河谷下切完成10年后左岸边坡的蠕变变形。
2.4 计算参数与本构模型采用清华大学自主研发的TFINE计算程序[24-25]进行参数计算。
2.4.1 弹塑性计算模型河谷下切数值模拟遵循Drucker-Prager屈服准则,并采用弹塑性模型进行计算,表示如下:
| $ F=\alpha I_1+\sqrt{J_2}-k \leqslant 0 . $ | (1) |
其中:F为岩体强度;I1为应力的第一不变量;J2为应力偏量的第二不变量;α、k分别为岩石内摩擦角和凝聚力相关参数。
I1和J2表示如下:
| $ I_1=\sigma_1+\sigma_2+\sigma_3, $ | (2) |
| $ J_2=\frac{1}{6}\left[\left(\sigma_1-\sigma_2\right)^2+\left(\sigma_2-\sigma_3\right)^2+\left(\sigma_3-\sigma_1\right)^2\right] . $ | (3) |
其中σ1、σ2、σ3为主应力。α和k通过Mohr-Coulomb准则得出。对于平面,若Drucker-Prager准则是Coulomb六边形的外接圆,则
| $ \alpha_1=\frac{2 \sin \varphi}{\sqrt{3}(3-\sin \varphi)}, $ | (4) |
| $ k_1=\frac{6 c \cos \varphi}{\sqrt{3}(3-\sin \varphi)}. $ | (5) |
其中φ和c为岩体的内摩擦角和凝聚力。若Drucker-Prager准则是Coulomb六边形的内接圆,则
| $ \alpha_2=\frac{2 \sin \varphi}{\sqrt{3}(3+\sin \varphi)}, $ | (6) |
| $ k_2=\frac{6 c \cos \varphi}{\sqrt{3}(3+\sin \varphi)} . $ | (7) |
TFINE实际采用:
| $ \alpha=\frac{1}{2}\left(\alpha_1+\alpha_2\right), $ | (8) |
| $ k=\frac{1}{2}\left(k_1+k_2\right) . $ | (9) |
计算参数如表 3所示。
| 岩体 | 变形模量E0 | Poisson比μ | 密度ρ | 摩擦因数f | 凝聚力c |
| GPa | 103 kg·m-3 | MPa | |||
| 基岩 | 22.00 | 0.25 | 2.80 | 1.35 | 2.00 |
| 煌斑岩脉 | 3.00 | 0.35 | 2.75 | 0.60 | 0.40 |
| 断层 | 0.56 | 0.35 | 2.60 | 0.30 | 0.02 |
2.4.2 蠕变本构模型
关于岩体长期变形的研究结果比较丰富,许多传统流变模型已应用于工程实践,但其本构方程很难刻画岩体内部结构变化和能量演化过程。本文蠕变计算采用基于内变量热力学的蠕变损伤模型[26]。在该模型中,采用内变量χ表征因蠕变变形使材料内部结构改变而在材料内部发生的损伤。内变量γ、λ与黏弹性、黏塑性变形有关,表征因蠕变变形使材料内部微结构变化而表现的宏观黏弹性、黏塑性变形,对应的本构方程表示如下:
| $ \dot{\boldsymbol{\varepsilon}}=\dot{\boldsymbol{\varepsilon}}^{\mathrm{e}}+\dot{\boldsymbol{\varepsilon}}^{\mathrm{ve}}+\dot{\boldsymbol{\varepsilon}}^{\mathrm{vp}}, $ | (10) |
| $ \dot{\boldsymbol{\varepsilon}}^{\mathrm{e}}=\boldsymbol{C}: \dot{\boldsymbol{\sigma}}, $ | (11) |
| $ \dot{\boldsymbol{\varepsilon}}^{\mathrm{ve}}=\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{\sigma}} \dot{\gamma}+\frac{\partial}{\partial \chi}\left(\frac{\partial \boldsymbol{A}}{\partial \boldsymbol{\sigma}} \gamma\right) \dot{\chi}, $ | (12) |
| $ \dot{\boldsymbol{\varepsilon}}^{\mathrm{vp}}=\frac{\partial P_i}{\partial \boldsymbol{\sigma}} \dot{\lambda}_i+\frac{\partial}{\partial \chi}\left(\frac{\partial P_i}{\partial \boldsymbol{\sigma}} \lambda_i\right) \dot{\chi} . $ | (13) |
其中:
工况1河谷下切过程主拉应力σ3如图 5所示。σ3等值线分布较均匀,云图沿河谷呈基本对称分布,但在断层处出现突变。随着河流逐级下切,σ3最大值逐渐减小,在相同高程处,坡体内部岩体的σ3值高于坡体表层岩体,且呈由内向外逐渐减小趋势,这表明河谷下切对边坡有明显卸荷作用。此外,河谷下切过程中,谷底岩体出现应力集中,其σ3值高于同高程其他岩体,第5次下切最明显,这一规律与文[16]的研究一致。值得注意的是:最大主应力以压应力为主,随着下切进行,部分区域出现拉应力,并且左岸拉应力区域大于右岸。
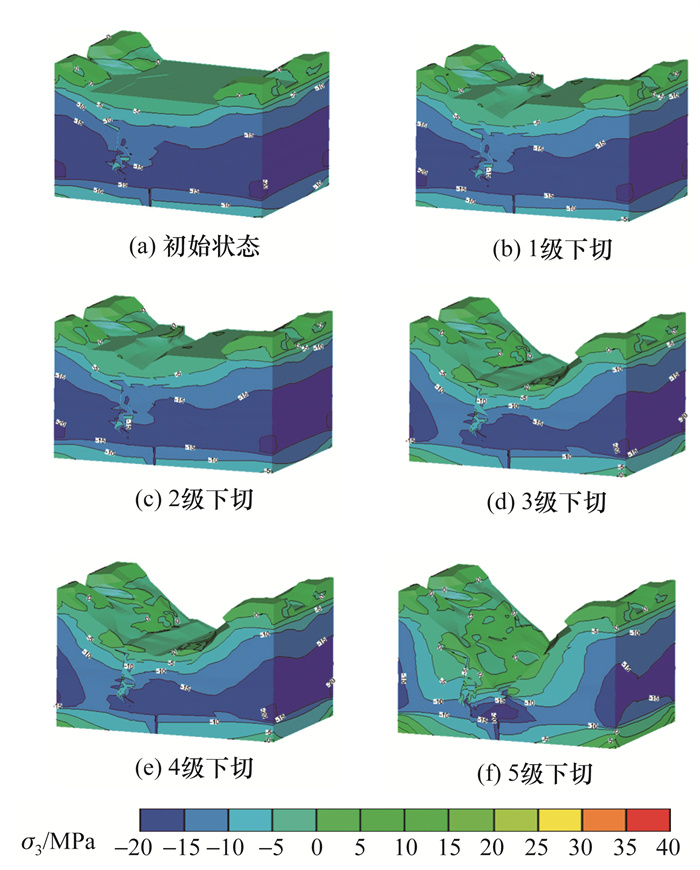
|
| 图 5 工况1下切过程σ3值云图 |
工况1河谷下切过程主压应力σ1如图 6所示。σ1值由坡体表面向坡体内部逐渐增大,随河谷下切应力释放而逐渐减小。此外,受构造应力影响,在下切过程的河谷底部、断层等软弱地质条件附近,以及左岸边坡坡岸与河谷下切部分的交界处出现应力集中现象。左岸边坡既有因河谷下切形成的应力释放区,体现为σ1值减小;又有因构造应力影响形成的应力集中区,体现为σ1值大于同高程其他岩体。
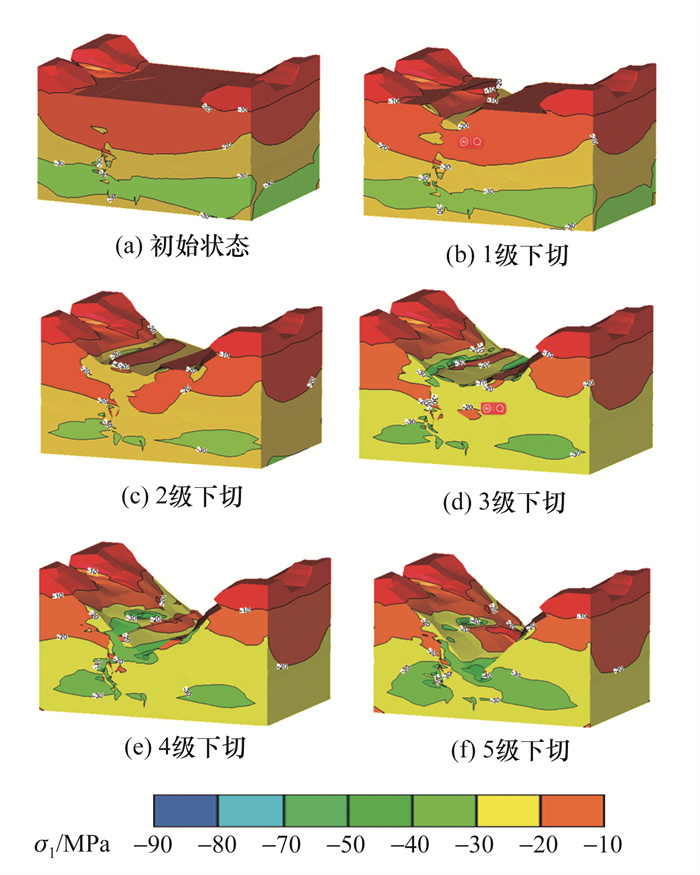
|
| 图 6 工况1下切过程σ1值云图 |
3.2 深部裂缝影响因素
图 7为3~5级下切1 930 m高程的σ3值剖面云图。随着下切进行,模型深部裂缝位置对应的σ3值不断减小,在4级下切时,煌斑岩脉X向坡外的岩体出现拉应力,5级下切时拉应力区域扩大至煌斑岩脉X以内区域。由于岩体抗拉性较弱,因此河谷下切形成的拉应力达到一定程度会造成该位置岩体破坏,拉应力向岩体深部发展形成深部裂缝。
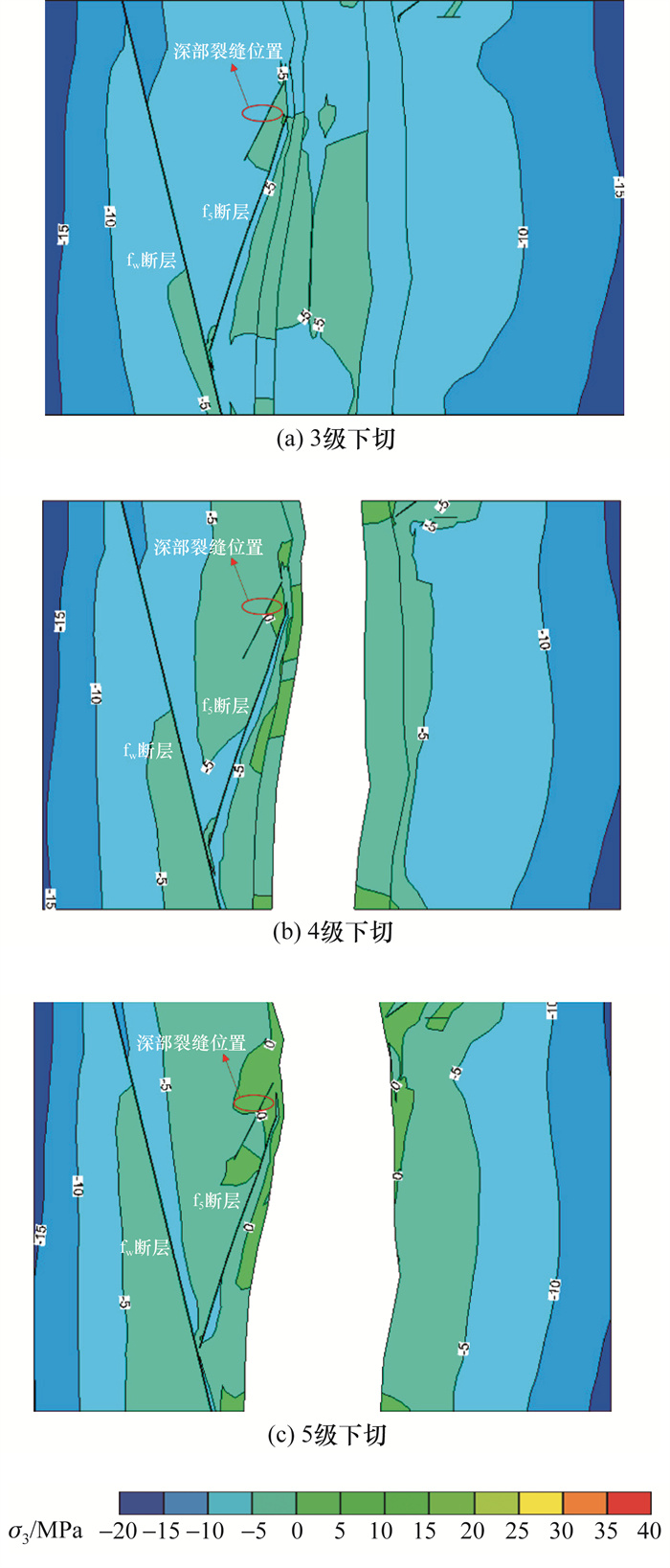
|
| 图 7 1 930 m高程水平剖面σ3值云图 |
图 7中河谷下切在右岸形成的拉应力区主要分布在坡体表层位置,而左岸受煌斑岩脉X和断层f5影响,拉应力区扩展至深部裂缝区域。此外,左岸拉应力区比右岸发育得更深,这与左岸发育深部裂缝和右岸极少发育深部裂缝的工程实践相符。由此可知,锦屏左岸边坡复杂地质条件(煌斑岩脉、断层等软弱带)是形成深部裂缝的原因之一。图 8为2种工况下深部裂缝位置对应的横河向剖面σ3值云图。无论是否施加构造应力,随着河谷下切进行,深部裂缝位置的σ3值不断减小,呈现明显的卸荷特征。如不考虑构造应力,煌斑岩脉X向坡内的岩体未出现拉应力,而1 930 m高程PD44平洞附近深部裂缝分布在煌斑岩脉X两侧;在施加构造应力情况下,左岸拉应力区域深度明显增加,并且在5级下切后煌斑岩脉X两侧均出现拉应力,与工程实践深部裂缝分布位置相符。这表明:构造应力使边坡卸荷深度加深,锦屏左岸边坡构造应力作用下的高地应力特征是形成深部裂缝的原因之一。
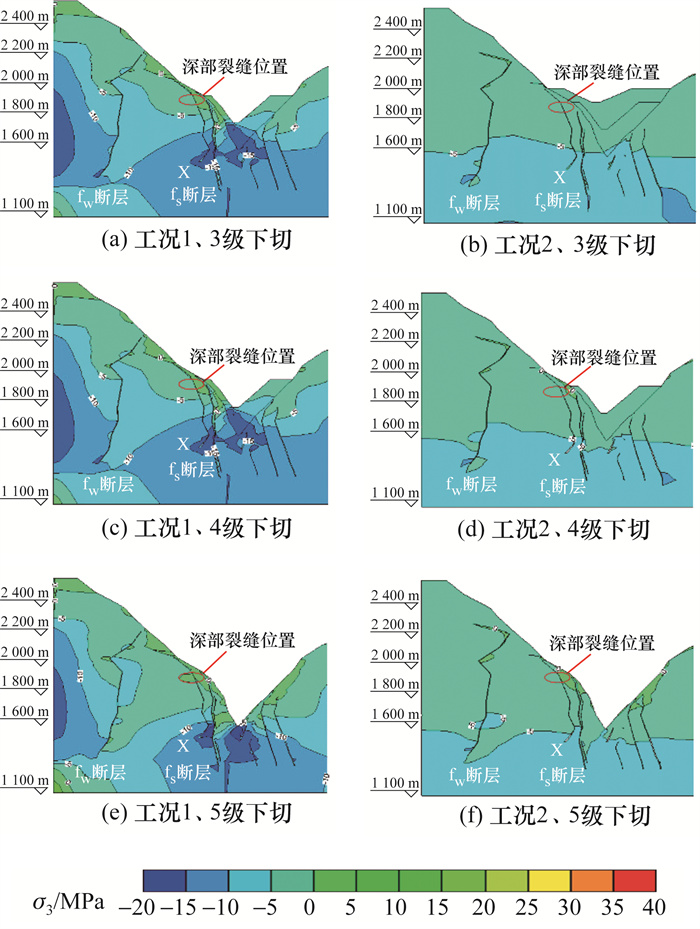
|
| 图 8 横河向剖面σ3值云图 |
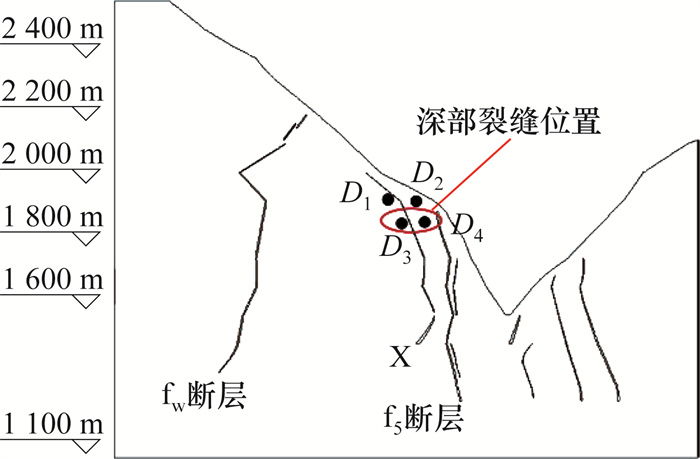
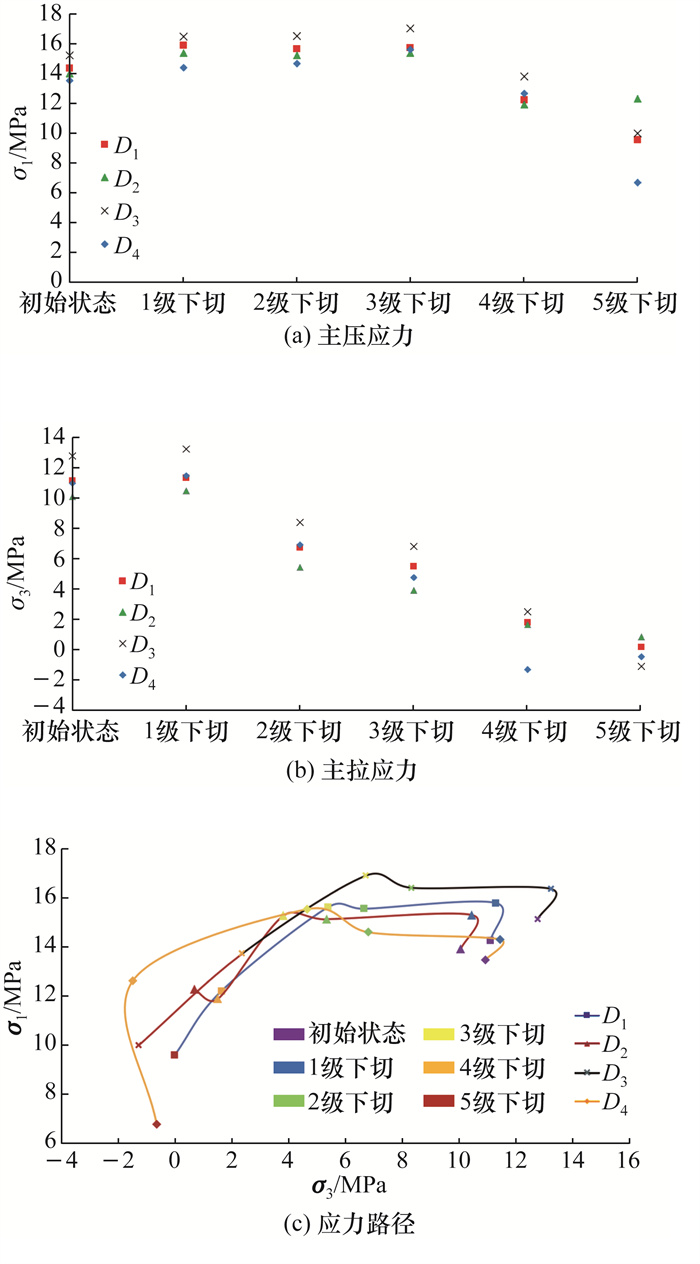
为分析应力变化情况,选取4个模型观测点,如图 9所示。观测点的主应力变化和应力路径曲线如图 10所示。在河谷下切初期,主压应力σ1增大,但变化不明显。在3级下切完成后,σ1开始下降,并且深部裂缝位置D3、D4降幅比D1、D2更大。主拉应力σ3随下切过程逐渐减小,D3、D4在5级下切完成后均出现拉应力。从图 10c中可知:初始状态深部裂缝部位岩体在高地应力作用下,σ1和σ3较大,岩体积累了较高的弹性应变能;在河谷演化初期(4级下切前),σ1小幅上升、σ3不断减小,岩体的弹性应变能处于缓慢释放状态;在河谷下切后期(4级下切开始后),σ1较小、σ3持续下降,岩体的弹性应变能快速释放,造成岩体卸荷张裂。这种破坏为典型的高地应力破坏,破坏过程伴随强烈的能量释放现象。
|
| 图 9 深部裂缝位置观测点分布 |
|
| 图 10 观测点主应力变化和应力路径 |
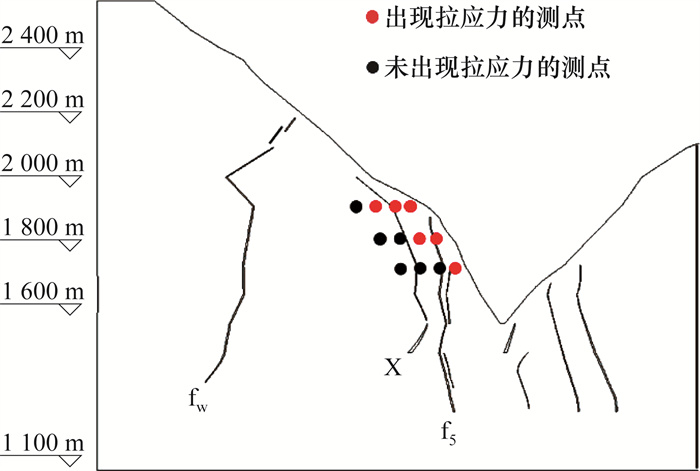
为分析低高程1 780 m深部裂缝的成因,取1 930、1 850、1 750 m高程50、100、200、250 m不同深度观测点,如图 11所示。记录其下切完成后的主应力值,如表 4所示。图 11中红点为河谷下切过程中出现σ3的测点。由图可知,出现σ3的区域主要在较浅位置,即1 700~1 930 m高程,且随着高程增加,卸荷深度逐渐增大。1 930 m高程出现拉应力的深度最大,约200~250 m。这与1 930 m高程出现深卸荷和1 780 m高程具有浅表层卸荷带的地质现象相符。
|
| 图 11 观测点位置分布 |
| 高程/m | 深度/m | σ1/MPa | σ2/MPa | σ3/MPa | σ1/σ3 |
| 1930 | 50 | -1.48 | -1.48 | -1.48 | — |
| 100 | 12.04 | 9.96 | 0.81 | 14.96 | |
| 200 | 17.55 | 14.28 | -0.29 | — | |
| 250 | 18.92 | 14.97 | 0.63 | 29.94 | |
| 1850 | 50 | 12.17 | 11.91 | 1.21 | 10.08 |
| 100 | 12.83 | 12.25 | -1.48 | — | |
| 200 | 14.74 | 12.38 | 2.45 | 6.01 | |
| 250 | 20.55 | 15.37 | 2.53 | 8.13 | |
| 1750 | 50 | 20.41 | 14.24 | -1.12 | — |
| 100 | 16.68 | 13.43 | 2.90 | 5.75 | |
| 200 | 23.16 | 15.83 | 4.26 | 5.43 | |
| 250 | 17.14 | 8.69 | 4.27 | 4.01 | |
| 注:表中“—”表示σ3出现拉应力。 | |||||
当岩体σ1/ σ3小于一定值(5~7),而σ1较大时,岩体在剪应力和压应力的共同作用下容易被压碎,这种破坏方式称为压剪破坏,通常伴随着垂直裂缝和斜裂缝。对于1 930 m高程,岩体的破坏方式主要为张拉破坏。50、100、200 m深度的测点在下切过程中均出现拉应力;250 m深度的测点5级下切后σ1/ σ3=29.9,远大于5~7,未发生压剪破坏。对于1 850 m高程:50、100 m深度的测点在下切过程中最小主应力出现拉应力,岩体浅表层可能产生拉破坏;200 m深度σ1/ σ3=6.01,在5~7范围内,岩体偏安全;250 m深度σ1/ σ3=8.13,岩体安全。对于1 750 m高程:浅层50 m深度的测点在下切过程中最小主应力出现拉应力,岩体浅层可能产生拉破坏;随着深度加大,σ1/ σ3逐渐减小,压剪破坏的风险增加,100和200 m深度σ1/ σ3分别为5.75和5.43,在5~7范围内,岩体偏安全;而在250 m深度σ1/ σ3仅为4.01,有发生压剪破坏的可能性。该规律与表层有卸荷,向边坡深部延伸初期未出现卸荷裂缝,再延伸300 m左右又出现卸荷裂缝的深部裂缝地质现象相符。
综上所述:高高程1 930 m深部裂缝的成因是河谷下切过程中边坡岩体深卸荷,深部压应力减小,甚至出现拉应力,在河谷下切后期发生弹性应变能快速释放,造成岩体卸荷张拉破坏;低高程1 780 m深部裂缝的成因是河谷下切过程中,左岸边坡仅表层卸荷明显,下切底部出现应力集中,随着深度加深,σ1/ σ3逐渐减小,且σ1、σ3均较大,最终在岩体深部发生压剪破坏。
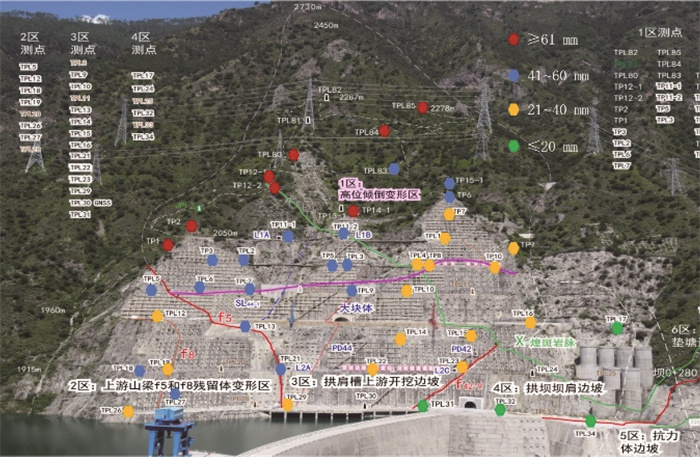
4 深部裂缝对边坡变形的影响 4.1 基于监测资料的边坡变形规律图 12(背景来自文[7])为运行期2014年8月24日至2022年7月29日锦屏左岸边坡表观测点分布与临空向变形情况,红点为变形量大于60.0 mm的测点。从空间分布来看,靠近坝肩测点的变形量大于远离坝肩测点,坝体拱推力对边坡临空向变形有阻碍作用。高高程位置表观变形大于低高程位置,表观变形主要来源于高高程区域的重力倾倒变形。
|
| 图 12 表观测点分布与变形情况 |
1 930 m高程平洞位置如图 13所示(背景来自文[7]),PD42和PD44平洞分别布设了石墨杆收敛计,图 14为石墨杆收敛计变形情况。PD42-1-1—PD42-1-6为PD42平洞7点石墨杆收敛计测段编号;PD42-2-1—PD42-2-11为PD42平洞12点石墨杆收敛计测段编号;PD44-1—PD44-12为PD44平洞石墨杆收敛计测段编号。
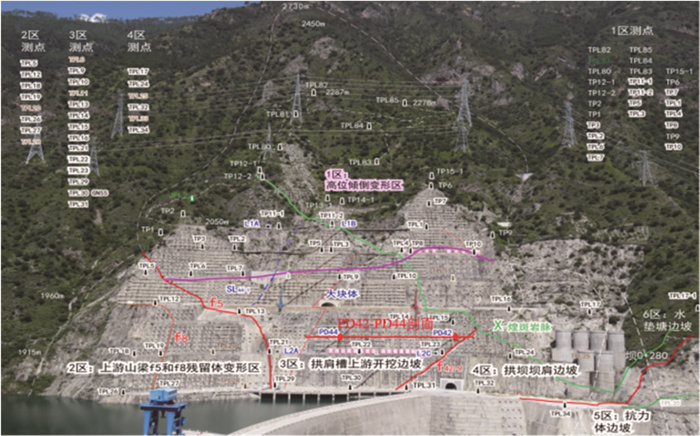
|
| 图 13 1 930 m高程平洞位置图 |
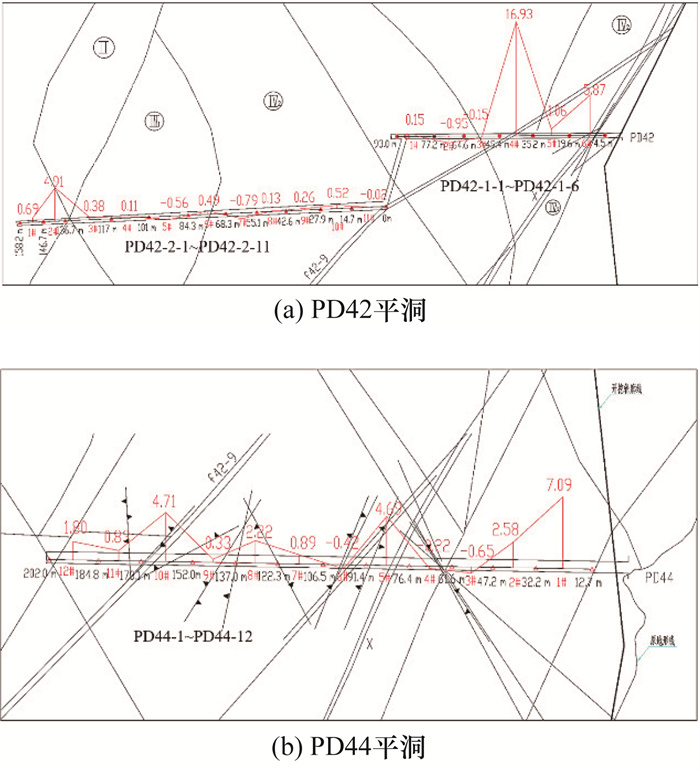
|
| 图 14 1 930 m高程石墨杆收敛计测点变形情况 |
图 14中大部分测点变形量在5.0 mm以内,变形情况较稳定。断层f42-9穿过的测段PD42-1-4运行期变形量最大,达16.9 mm。煌斑岩脉、断层穿过的测段运行期变形量较大,说明煌斑岩脉、断层等对边坡深部变形起控制作用。PD44穿过深部裂缝发育区域,除有煌斑岩脉、断层经过的测段外,其他区域的变形量相对较小且波动不明显,这说明深部裂缝对深部变形的影响较小。
为进一步分析深部裂缝对边坡整体变形的影响,本文对比了表观变形和深部变形,选取PD42平洞最近的表观测点TPL23,绘制临空向变形曲线,并与PD42平洞7点石墨杆收敛计PD42-1和12点石墨杆收敛计PD42-2进行对比分析(见图 15)。
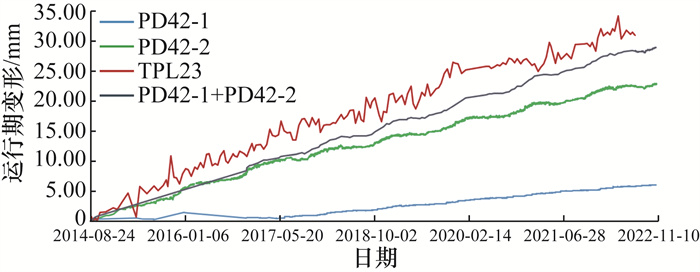
|
| 图 15 表观变形和深部变形对比 |
图 15中PD42平洞2测段之和的变形规律与TPL23基本一致,变形量接近。整个运行期PD42平洞2测段总变形量为29.0 mm(拉伸变形),而TPL23表观测点临空向变形量为30.1 mm,二者变形量接近,可认为PD42平洞的最深点为不动点。对比结果可知:表观变形与深部变形相互对应,说明变形资料可靠;边坡表观临空向变形来自边坡内部较深部位的变形,而不受PD42平洞最深点以内较深部位岩体的影响。煌斑岩脉、断层等对边坡深部变形起控制作用,深部裂缝对边坡变形的影响较小。
4.2 基于蠕变模拟的边坡长期变形规律如2.4节所述,蠕变计算未考虑构造应力的影响,依据如下:3.2节中对是否考虑构造应力的影响进行对比,发现构造应力是造成边坡向深部卸荷形成深部裂缝的原因之一;而通过分析监测资料发现深部裂缝对边坡变形的影响不明显,且边坡变形不受PD42平洞最深点以内较深部位岩体的影响,构造应力未传递至PD42平洞深度范围内的岩体。因此,本文认为形成深部裂缝后,构造应力作用对边坡变形的影响已经消散。
蠕变计算结果如图 16所示,边坡横河向变形在下切完成10年后仍未达到稳定状态,而边坡竖直向蠕变变形在河谷下切完成后第6年达到稳定状态。实测监测资料显示,左岸边坡竖直向变形量极小且已达到稳定状态,而高高程横河向变形仍在持续发展,进一步印证了构造应力对边坡变形的影响已经消散。
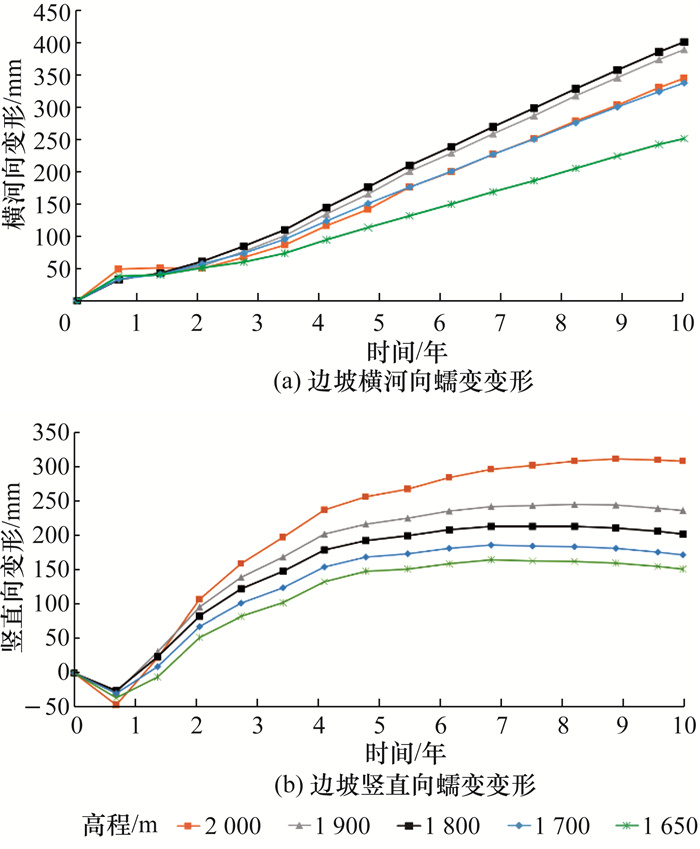
|
| 图 16 边坡蠕变变形随高程分布情况 |
5 结论
本文通过建立锦屏坝址区三维模型模拟河谷下切,分析了锦屏左岸边坡深部裂缝的成因和力学机制;通过分析实测监测资料和边坡岩体蠕变计算,研究深部裂缝对边坡变形的影响,得出如下结论:
1) 本文通过数值模拟分析河谷下切、复杂地质条件、构造应力对锦屏左岸边坡地应力的影响。结果表明:锦屏左岸边坡深部裂缝是在边坡特定地质条件下,受河谷下切和构造应力影响,发生应力释放和重分布,在原有结构面基础上形成的深部张拉裂缝。
2) 从力学机制角度看:1 930 m高程局部岩体在河谷下切后期,从表层到深部发生弹性应变能快速释放,造成岩体卸荷破坏形成卸荷裂缝;1 780 m高程岩体,虽仅边坡表层卸荷明显,但随着深度增加,主拉应力和主压应力逐渐接近,且主压应力较大,最终发生压剪破坏。
3) 从变形监测资料来看,PD44平洞附近表观变形和深部变形接近。平洞最深处可认为是不动点。本文通过深部变形分析,认为控制锦屏左岸边坡变形的主要因素是煌斑岩脉、断层等软弱带,而深部裂缝对边坡变形的影响较小。
4) 随着河谷下切,边坡深部卸荷,在边坡表层、深部发育裂缝后,构造应力的影响已经消散。边坡更深处岩体可能还受构造应力的影响,但对边坡变形影响较小。施加构造应力存在量值难以确定、边界难以处理等问题。因此,在进行边坡整体稳定性分析、边坡与拱坝的相互作用、边坡长期变形规律等数值计算研究时可不考虑构造应力的影响。
| [1] |
王小群, 王兰生, 沈军辉, 等. 西南某电站坝址区岸坡深裂缝分布规律[J]. 重庆大学学报(自然科学版), 2003, 26(9): 14-17. WANG X Q, WANG L S, SHEN J H, et al. Disquisition on distributing law of bank slope deep fracture of an electricity station dam site section at southwest[J]. Journal of Chongqing University (Natural Science Edition), 2003, 26(9): 14-17. (in Chinese) |
| [2] |
陈鸿. 大渡河中下游典型岸坡深部裂缝形成机制及工程效应研究[D]. 成都: 成都理工大学, 2005. CHEN H. A study on the formation mechanic and engineering effect of deep crack in typical slopes of middle and lower reaches of the Dadu River [D]. Chengdu: Chengdu University of Technology, 2005. (in Chinese) |
| [3] |
黄润秋, 王士天, 张倬元, 等. 中国西南地壳浅表层动力学过程及其工程环境效应研究[M]. 成都: 四川大学出版社, 2001. HUANG R Q, WANG S T, ZHANG Z Y, et al. The dynamic process of earth's superficial crust and its engineering environmental effects in southwestern of China[M]. Chengdu: Sichuan University Press, 2001. (in Chinese) |
| [4] |
韩文峰. 黄河黑山峡大柳树松动岩体工程地质研究[M]. 兰州: 甘肃科学技术出版社, 1993. HAN W F. Engineering geological research on the loose rock mass at Daliushu of Heishan Gorge in Yellow River[M]. Lanzhou: Gansu Science & Technology Press, 1993. (in Chinese) |
| [5] |
杨永明. 苗家坝水电站坝区加坡典型楔形体的变形破坏特征[J]. 甘肃电力, 1995(2): 28-33, 51. YANG Y M. The deformation and damage character of typical wedge in abutment slope at Miaojiaba Hydropower Station[J]. Gansu Electric, 1995(2): 28-33, 51. (in Chinese) |
| [6] |
韩刚, 赵其华, 彭社琴. 白鹤滩水电站坝区深部破裂岩体地应力演化特征[J]. 岩土力学, 2011, 32(S1): 583-589. HAN G, ZHAO Q H, PENG S Q. In-situ stress field evolution of deep fracture rock mass at dam area of Baihetan Hydropower Station[J]. Rock and Soil Mechanics, 2011, 32(S1): 583-589. (in Chinese) |
| [7] |
梁靖, 裴向军, 罗路广, 等. 锦屏一级水电站左岸高边坡变形监测及稳定性分析[J]. 水利水电技术(中英文), 2021, 52(4): 180-185. LIANG J, PEI X J, LUO L G, et al. Deformation monitoring and stability analysis of left bank highslope at Jinping I Hydropower Station[J]. Water Resources and Hydropower Engineering, 2021, 52(4): 180-185. (in Chinese) |
| [8] |
周绿, 刘明昌. 锦屏一级水电站运行期左岸边坡稳定性分析[J]. 水利水电快报, 2021, 42(6): 26-30. ZHOU L, LIU M C. Stability analysis of slope on left bank of Jinping I Hydropower Station during operation period[J]. Express Water Resources & Hydropower Information, 2021, 42(6): 26-30. (in Chinese) |
| [9] |
梁瑶. 深切河谷地区的地应力场研究和高边坡稳定性评价[D]. 成都: 西南交通大学, 2009. LIANG Y. The study of in situ stress and rock slope stability analysis in deep-incised valley [D]. Chengdu: Southwest Jiaotong University, 2009. (in Chinese) |
| [10] |
SHAN Z G, NI W D, LIU A. Numerical simulation of in-situ stress field characteristics about the dam site area of Baihetan Hydropower Station[J]. Journal of Physics: Conference Series, 2022, 2202(1): 012008. DOI:10.1088/1742-6596/2202/1/012008 |
| [11] |
梁瑶, 赵刚, 杨涛. 考虑侵蚀下切作用的深切河谷岩体地应力场回归[J]. 西南交通大学学报, 2009, 44(4): 569-573. LIANG Y, ZHAO G, YANG T. Multi-regression analysis of in-situ stress field in deep river valley[J]. Journal of Southwest Jiaotong University, 2009, 44(4): 569-573. DOI:10.3969/j.issn.0258-2724.2009.04.017 (in Chinese) |
| [12] |
周勇, 李啟常, 潘兵, 等. 杨房沟水电站深切河谷地应力场反演分析[J]. 人民长江, 2018, 49(24): 44-48, 71. ZHOU Y, LI Q C, PAN B, et al. Back analysis of initial geostress field in deep-cut valley of Yangfanggou Hydropower Station[J]. Yangtze River, 2018, 49(24): 44-48, 71. (in Chinese) |
| [13] |
祁生文, 伍法权, 兰恒星. 锦屏一级水电站普斯罗沟左岸深部裂缝成因的工程地质分析[J]. 岩土工程学报, 2002, 24(5): 596-599. QI S W, WU F Q, LAN H X. Study on the mechanism of the deep fractures of the left abutment slope at the Jinping First Stage Hydropower Station[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 596-599. DOI:10.3321/j.issn:1000-4548.2002.05.012 (in Chinese) |
| [14] |
祁生文, 伍法权, 丁振明, 等. 从工程地质类比的角度看锦屏一级水电站左岸深部裂缝的形成[J]. 岩石力学与工程学报, 2004, 23(8): 1380-1384. QI S W, WU F Q, DING Z M, et al. Study on mechanism of deep fractures of Jinping First Stage Hydropower Station by engineering geology analogy[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1380-1384. DOI:10.3321/j.issn:1000-6915.2004.08.028 (in Chinese) |
| [15] |
荣冠, 朱焕春, 王思敬. 锦屏一级水电站左岸边坡深部裂缝成因初探[J]. 岩石力学与工程学报, 2008, 27(S1): 2855-2863. RONG G, ZHU H C, WANG S J. Primary research on mechanism of deep fractures formation in left bank of Jinping First Stage Hydropower Station[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1): 2855-2863. (in Chinese) |
| [16] |
徐佩华, 黄润秋, 陈剑平, 等. 高地应力区复杂结构河谷应力场特征: 以锦屏Ⅰ级水电站为例[J]. 吉林大学学报(地球科学版), 2013, 43(5): 1523-1532. XU P H, HUANG Y Q, CHEN J P, et al. Stress field characteristics of a valley slope with complex geological structure in high geo-stress area: A case of Jinping I Hydropower Station[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(5): 1523-1532. (in Chinese) |
| [17] |
黄润秋. 论中国西南地区水电开发工程地质问题及其研究对策[J]. 地质灾害与环境保护, 2002, 13(1): 1-5. HUANG R Q. Discussion on the main engineering geological problems in hydropower development in southwestern China and their research strategies[J]. Journal of Geological Hazards and Environment Preservation, 2002, 13(1): 1-5. DOI:10.3969/j.issn.1006-4362.2002.01.001 (in Chinese) |
| [18] |
黄润秋. 中国西南岩石高边坡的主要特征及其演化[J]. 地球科学进展, 2005, 20(3): 292-297. HUANG R Q. Main characteristics of high rock slopes in southwestern China and their dynamic evolution[J]. Advances in Earth Science, 2005, 20(3): 292-297. DOI:10.3321/j.issn:1001-8166.2005.03.005 (in Chinese) |
| [19] |
王运生, 罗永红, 吴俊峰, 等. 中国西部深切河谷谷底卸荷松弛带成因机理研究[J]. 地球科学进展, 2008, 23(5): 463-468. WANG Y S, LOU Y H, WU J F, et al. Study on the genetic mechanism of unloaded and relaxed zone in the deep river valley bottom, West of China[J]. Advances in Earth Science, 2008, 23(5): 463-468. DOI:10.3321/j.issn:1001-8166.2008.05.004 (in Chinese) |
| [20] |
侯孝东. 河流快速下切对岸坡岩体卸荷深度的影响研究[D]. 成都: 成都理工大学, 2021. HOU X D. Study on the influence of rapid river undercutting on unloading depth bank slope rock mass [D]. Chengdu: Chengdu University of Technology, 2021. (in Chinese) |
| [21] |
柴建峰, 祁生文, 滕开永, 等. 高山峡谷地区高陡边坡深部裂缝一般特征分析[J]. 工程地质学报, 2007, 15(6): 730-738. CHAI J F, QI S W, TENG K Y, et al. Spectial characteristics of deep fractures in high and steep slopes in southwestern of China[J]. Journal of Engineering Geology, 2007, 15(6): 730-738. DOI:10.3969/j.issn.1004-9665.2007.06.002 (in Chinese) |
| [22] |
钟传贵. 库水作用下锦屏一级坝区左岸工程边坡稳定性研究[D]. 成都: 成都理工大学, 2018. ZHONG C G. Under the action of reservoir water kam screen level in the left bank of the reservoir engineering slope stability research [D]. Chengdu: Chengdu University of Technology, 2018. (in Chinese) |
| [23] |
赵德军, 陈洪德, 吴德超. 雅砻江锦屏一级水电站左岸深部裂缝成因机制探讨[J]. 水文地质工程地质, 2011, 38(6): 102-107. ZHAO D J, CHEN H D, WU D C. Discussion of the formation of deep fractures on the left bank of the Jinping I Hydropower Station of the Yalong River[J]. Hydrogeology & Engineering Geology, 2011, 38(6): 102-107. (in Chinese) |
| [24] |
周维垣. 岩体工程结构的稳定性[J]. 岩石力学与工程学报, 2010, 29(9): 1729-1753. ZHOU W Y. Structure stability of rock mass engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1729-1753. (in Chinese) |
| [25] |
LIU Y R, WU Z S, YANG Q, et al. Dynamic stability evaluation of underground tunnels based on deformation reinforcement theory[J]. Advances in Engineering Software, 2018, 124: 97-108. DOI:10.1016/j.advengsoft.2018.08.007 |
| [26] |
ZHANG L, LIU Y R, YANG Q. A creep model with damage based on internal variable theory and its fundamental properties[J]. Mechanics of Materials, 2014, 78: 44-55. DOI:10.1016/j.mechmat.2014.07.017 |



