2. 同济大学 土木工程防灾国家重点实验室, 上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
随着中国交通建设不断发展,越来越多的隧道和地下工程将穿越具有强烈流变特性的软岩地层。在软岩隧道开挖和支护的过程中,岩石流变将造成与时间相关的围岩-衬砌相互作用,威胁衬砌结构的安全[1]。此外,高水压环境中地下结构往往面临渗漏风险[2],需要考虑渗流对隧道稳定性的影响。因此,在隧道设计和稳定性评估中,全面考虑岩石流变、与时间相关的施工过程和渗流影响尤为重要。
针对流变问题,目前常基于合理数学力学模型进行数值与理论分析。其中,解析解能够以函数形式清晰地揭示流变参数的影响,并为数值分析的正确性提供基准。目前,众多不同的黏弹塑性模型[3-5]在解决软岩隧道或井壁问题时仅获得单一力场解析解,且理论推导在处理特有的塑性卸载问题时存在简化,所得结果与实际情况可能存在差异。渗流影响下的力场问题多针对弹塑性问题,且均未考虑与时间相关的非稳态渗流场[6-8]。在井壁稳定性问题中,Hu等[9]针对非稳态渗流/温度场引起的水合物分解和井壁稳定问题,采用Laplace变换求解不同工况下各区域的黏弹塑性解析解,但此类解析方法仅可用于隧道开挖阶段。工程力学响应与应力路径密切相关。隧道开挖阶段,由于地应力被释放,因此围岩从弹性状态达到塑性状态,从弹塑性力学角度看,该过程称为“加载”;而支护后由于地应力作用下已经发生流变的围岩仍在持续变形,因此,围岩和衬砌相互作用产生了随时间增大的支护力,使围岩从塑性段“卸载”至弹性段,但塑性变形不可恢复。只有正确考虑全施工过程加卸载应力路径,才可以获得正确的围岩、衬砌力学响应[4, 10-11]。文[12-13]考虑了黏弹塑性问题中加卸载应力路径,结合实际施工中的支护技术——“先让后抗”“边让边抗”“先控再让后抗”,推导3种情况下围岩的黏弹塑性应力和位移,但是忽略了支护卸载前的塑性应变对卸载后的影响及卸载前塑性区的黏弹性应变,也没有考虑渗流对力场的影响。
综上,流变岩体中隧道稳定性和支护压力预测的解析研究尚未精确考虑开挖与支护全施工过程中的应力路径及非稳态渗流场的影响。因此,为更精准快速地预测与时间相关的支护结构受力变化和围岩稳定性,本文采用黏弹塑性模型模拟围岩流变,并考虑实际应力路径和非稳态渗流场的影响,推导衬砌支护下深埋圆形软岩隧道施工全过程应力和位移的精确解析解,为流变软岩中隧道工程建设提供理论支持,为隧道等地下工程的长期稳定提供保障。
1 问题描述本文针对渗流影响下深埋圆形隧道开挖和支护阶段中围岩力学状态进行分析。为便于解析解导出并保证简洁性,作出以下假设:
1) 隧道深埋,受各向等值初始地应力P0作用,地应力较大情况下可忽略计算深度内的重力梯度影响;围岩为连续、均匀、各向同性介质;隧道横断面尺寸远小于轴向长度,所考虑的横断面远离掘进工作面。
2) 采用黏弹塑性模型体现围岩流变特性并考虑围岩-衬砌真实相互作用,如图 1所示。该模型由广义Kelvin体单元和塑性单元组成,前者反映了围岩随时间变化的变形过程,后者反映了岩石的塑性屈服行为。图 1中,①为黏弹性部分,②为塑性部分。G(t)、K(t)分别为黏弹性模型的剪切和体积松弛模量,表示如下:
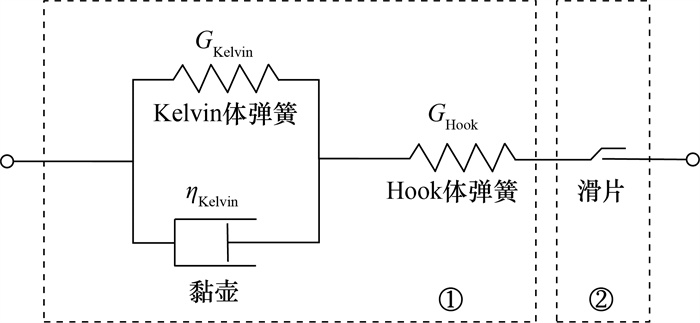
|
| 图 1 黏弹塑性模型 |
| $ \begin{aligned} G(t)= & \frac{G_{\text {Hook }}^2}{G_{\text {Hook }}+G_{\text {Kelvin }}} \exp \left(-\frac{G_{\text {Hook }}+G_{\text {Kelvin }}}{\eta_{\text {Kelvin }}} t\right)+ \\ & \frac{G_{\text {Hook }} G_{\text {Kelvin }}}{G_{\text {Hook }}+G_{\text {Kelvin }}}, \end{aligned} $ | (1) |
| $ K(t)=K_{\text {Hook }} . $ | (2) |
其中:t为时间;GKelvin和GHook分别为Kelvin体和Hook体的剪切模量;KHook为体应变模量;ηKelvin为黏性系数。当围岩处于弹性阶段时,遵循黏弹性本构模型。
3) 假定渗流仅发生在隧道截面所在平面。当初始孔压较大时,可以忽略初始压力梯度,考虑服从Darcy定律的水单相非稳态渗流过程;渗流压力影响力场,但未考虑力场对渗流场的影响,同时忽略了围岩因塑性变形造成的渗透系数变化和水对岩石特性的影响。
以下推导中,皆采用极坐标系(r, θ),取圆心为极点O,r为极径,θ为极角。符号约定如下:压应力和径向位移向洞室中心为正。由于本文问题是轴对称平面应变问题,因此剪应力、剪应变和切向位移均为零。
施工过程分为2个阶段。开挖阶段T1(0≤t < t1):当t=0时,隧道立即开挖;同时,在开挖阶段内,对隧道周边环境进行持续监测,确保衬砌施工安全。简化后的力学模型如图 2所示。其中,R0为隧道的开挖半径,Rpla为塑性区(plastic zone)半径。当R0 < r < Rpla时,区域为围岩的塑性区;当r>Rpla时,区域为围岩的黏弹性区。开挖阶段没有水流动,因此没有附加应力产生。该阶段只需分析开挖释放荷载下的单一力场。
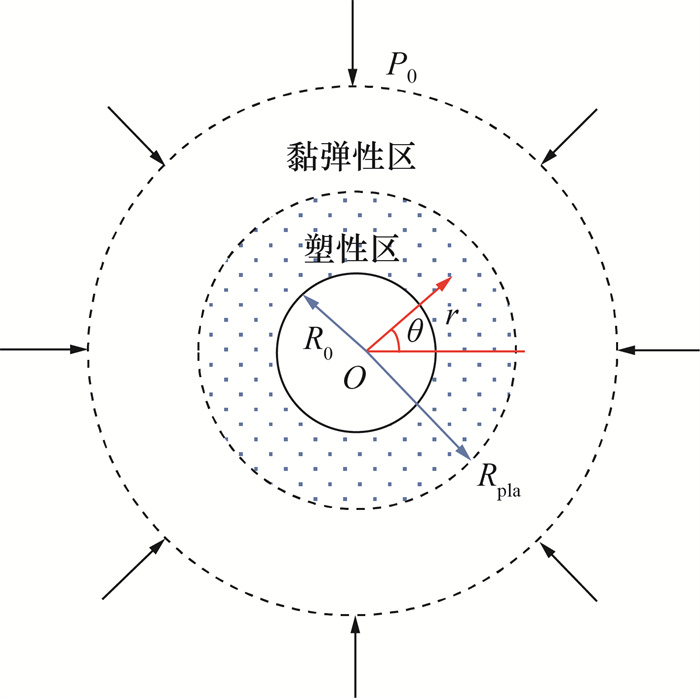
|
| 图 2 开挖阶段的力学简化模型 |
支护阶段T2(t≥t1):当t=t1时,施加衬砌。将衬砌视为弹性。图 3展示了该阶段的力学模型。其中R1为衬砌内径。该阶段内,由流变引发的支护力使围岩应力处于较安全的状态,即发生塑性卸载。由加卸载原理推导得到原塑性区全部卸载为卸载区,具体推导见2.3节。因此,在支护阶段,当R0 < r < Rpla时,所在区域定义为塑性卸载区。衬砌施加后,长期力学作用可能使支护或防水层出现裂缝或破坏,导致水渗漏或涌出,因此该阶段的力场分析需要考虑渗流场的影响。
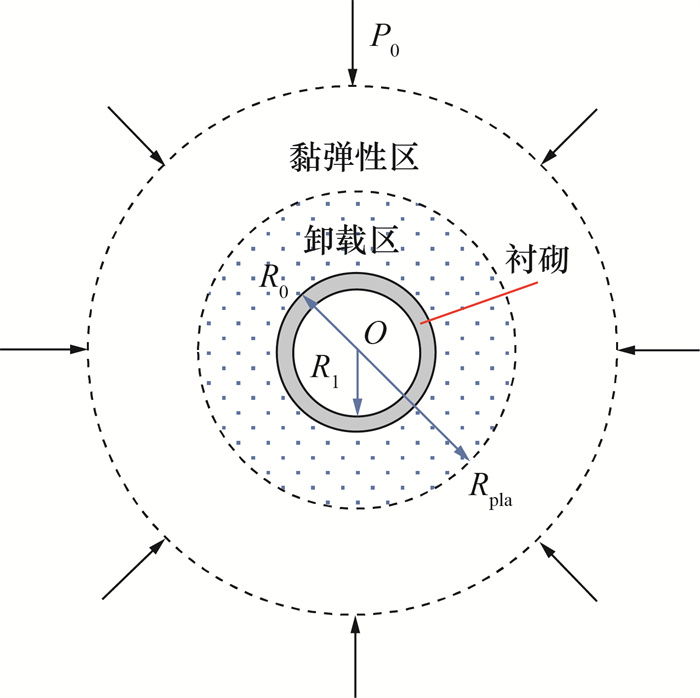
|
| 图 3 支护阶段的力学简化模型 |
2 全阶段解析解
本文考虑渗流影响,基于Mohr-Coulomb(MC)屈服准则并精确考虑开挖和支护全过程中围岩应力路径,严格推导短长期状态下围岩的应力和位移随时间变化的精确解析解。
孔隙压力(以下简称“孔压”)用pi(r, t)表示,其中i为区域编号,i=1, 2。在支护阶段,将围岩塑性卸载区定义为区域1,将衬砌区定义为区域2。
应力和位移分别为σc-da-b和uc-da-b, a表示应力/位移所处的时间阶段,a为T1或T2;b表示该变量属于黏弹性区域(viscoelastic zone)或塑性区域,b为ve或pla;c表示该变量的方向是径向或切向,c为r或θ;d表示属于塑性区域的黏弹性部分或塑性部分,d为ve或pla。
2.1 非稳态渗流场[14]对非稳态渗流场进行求解。对于该轴对称平面问题,非稳态渗流的孔隙压力场控制方程如下:
| $ \frac{1}{r} \cdot \frac{\partial p}{\partial r}+\frac{\partial^2 p}{\partial r^2}=\frac{1}{z} \cdot \frac{\partial p}{\partial t}, $ | (3) |
| $ z=\frac{k}{\mu \phi \Lambda} . $ | (4) |
其中:z为扩散系数或导压系数;k为渗透率;μ为流体黏度;ϕ为孔隙度;Λ为地层压缩系数。
令
| $ w=\frac{r^2}{4 z t} . $ |
采用分离变量法,求解可得
| $ \begin{gathered} p(w)=-A \int_w^{\infty} \frac{\exp (-w)}{w} \mathrm{~d} w+B=A \operatorname{Ei}(-w)+B, \\ \operatorname{Ei}(-w)=\int_w^{\infty} \frac{\exp (-w)}{w} \mathrm{~d} w . \end{gathered} $ |
其中:A和B为未知数;Ei(-w)为指数积分函数。进入支护阶段后,对于衬砌区和围岩塑性卸载区,则有
| $ p_i(r, t)=A_i \mathrm{Ei}\left(-\frac{r^2}{4 z_i t}\right)+B_i, \quad i=1, 2 . $ | (5) |
其中:式(5)共有4个未知数,即A1、B1、A2、B2。
边界处压差引发渗流,增量边界条件和协调条件表示如下:
| $ \left.\Delta p_2(r, t)\right|_{r=R_1}=p_{\text {tf }}-p_{\infty}, $ | (6) |
| $ \left.\Delta p_1(r, t)\right|_{r=R_0}=\left.\Delta p_2(r, t)\right|_{r=R_0}, $ | (7) |
| $ \left.\Delta p_1(r, t)\right|_{r \rightarrow \infty}=0, $ | (8) |
| $ \left.k_1 \frac{\mathrm{~d} \Delta p_1(r, t)}{\mathrm{d} r}\right|_{r=R_0}=\left.k_2 \frac{\mathrm{~d} \Delta p_2(r, t)}{\mathrm{d} r}\right|_{r=R_0} . $ | (9) |
其中:ptf为洞周处孔压;p∞为无穷远处的孔压;k1、k2分别为围岩塑性卸载区(区域1)和衬砌区(区域2)的渗透率。
将式(5)代入边界条件式(6)—(9),解得A1、B1、A2、B2。将结果代入,获得衬砌区的孔压Δp1(r, t)和围岩塑性卸载区的孔压Δp2(r, t),表示如下:
| $ \begin{gathered} \Delta p_1(r, t)=-\exp \left(\frac{R_0^2}{4 t z_1}\right) k_2\left(p_{\mathrm{tf}}-p_{\infty}\right) \cdot \\ \operatorname{Ei}\left(-\frac{r^2}{4 t z_1}\right) \cdot \gamma_1(t), \\ \Delta p_2(r, t)=\left[-\exp \left(\frac{R_0^2}{4 t z_2}\right) k_1 \operatorname{Ei}\left(-\frac{r^2}{4 t z_2}\right)+\gamma_2(t)\right] . \\ \left(p_{\mathrm{tf}}-p_{\infty}\right) \gamma_1(t), \\ \gamma_1(t)=\frac{1}{\left[\begin{array}{l} \exp \left(\frac{R_0^2}{4 t z_2}\right) \operatorname{Ei}\left(-\frac{R_0^2}{4 t z_2}\right) k_1 \\ -\exp \left(\frac{R_0^2}{4 t z_2}\right) \operatorname{Ei}\left(-\frac{R_1^2}{4 t z_2}\right) k_1 \\ -\exp \left(\frac{R_0^2}{4 t z_2}\right) \operatorname{Ei}\left(-\frac{R_0^2}{4 t z_1}\right) k_2 \end{array}\right]}, \\ \gamma_2(t)=\exp \left(\frac{R_0^2}{4 t z_2}\right) \operatorname{Ei}\left(-\frac{R_0^2}{4 t z_2}\right) k_1- \\ \exp \left(\frac{R_0^2}{4 t z_2}\right) \operatorname{Ei}\left(-\frac{R_0^2}{4 t z_1}\right) k_2 . \end{gathered} $ |
极坐标系下轴对称问题的平衡方程表示如下:
| $ \frac{\partial \sigma_r(r, t)}{\partial r}+\frac{\sigma_r(r, t)-\sigma_\theta(r, t)}{r}=0 . $ | (10) |
其中σr(r, t)和σθ(r, t)分别为径向和切向正应力。
几何方程表示如下:
| $ \varepsilon_r(r, t)=\frac{\partial u_r(r, t)}{\partial r}, \quad \varepsilon_\theta(r, t)=\frac{u_r(r, t)}{r} . $ | (11) |
其中:ur(r, t) 为径向位移;εr(r, t)和εθ(r, t)分别为径向应变和切向应变。
对于黏弹性区域,结合有效应力原理,其本构方程表示如下:
| $ \left\{\begin{array}{l} \boldsymbol{S}_{i j}(r, t)=2 G(t) * \mathrm{~d} \boldsymbol{e}_{i j}(r, t), \\ \sigma_{\mathrm{mm}}(r, t)-3 \alpha p_i(r, t)=3 K(t) * \mathrm{~d} \varepsilon_{\mathrm{mm}}(r, t) . \end{array}\right. $ | (12) |
| $ \left\{\begin{array}{l} \boldsymbol{S}_{i j}=\boldsymbol{\sigma}_{i j}-\frac{1}{3} \boldsymbol{\delta}_{i j} \Delta \sigma_{\mathrm{mm}}, \\ \boldsymbol{e}_{i j}=\boldsymbol{\varepsilon}_{i j}-\frac{1}{3} \boldsymbol{\delta}_{i j} \Delta \varepsilon_{\mathrm{mm}} . \end{array}\right. $ | (13) |
其中:“*”表示Stieltjes卷积;α为Biot系数;Sij(r, t)和eij(r, t)分别为应力偏张量和应变偏张量;σmm(r, t)和εmm(r, t)分别为体积应力和体积应变;σij和εij分别为应力张量和应变张量;δij为Kronecker对称张量。
r=Rpla位于黏弹性区域和塑性区域的界面处,其应力满足MC屈服准则(此时切向正应力为最大主应力),表示如下:
| $ \sigma_\theta(r, t)-M \sigma_r(r, t)-N=0, $ | (14) |
| $ M=\frac{1+\sin \varphi}{1-\sin \varphi}, $ | (15) |
| $ N=\frac{2 c \cos \varphi}{1-\sin \varphi} . $ | (16) |
其中:c为黏聚力,φ为内摩擦角。
边界条件如下:
| $ \sigma_r^{T_1, \text { pla }}\left(R_0, t\right)=0, $ | (17) |
| $ \sigma_r^{T_1, \text { ve }}(\infty, t)=P_0 . $ | (18) |
其中σrT1, pla和σrT1, ve分别为开挖阶段塑性区和黏弹性区的径向应力。
连续性条件如下:
| $ u_r^{T_1, \text { pla }}\left(R_{\mathrm{pla}}, t\right)=u_r^{T_1, \text { ve }}\left(R_{\mathrm{pla}}, t\right), $ | (19) |
| $ \sigma_r^{T_1, \text { pla }}\left(R_{\mathrm{pla}}, t\right)=\sigma_r^{T_1, \text { ve }}\left(R_{\mathrm{pla}}, t\right) . $ | (20) |
其中urT1, pla和urT1, ve分别为开挖阶段塑性区和黏弹性区的径向位移。
根据式(10)和(14)可得,在r=Rpla处,两区域的切向方向应力也相等,可表示为
| $ \sigma_\theta^{T_1, \text { pla }}\left(R_{\mathrm{pla}}, t\right)=\sigma_\theta^{T_1, \text { ve }}\left(R_{\mathrm{pla}}, t\right) . $ | (21) |
塑性区应变为弹性应变和塑性应变之和,表示如下:
| $ \left\{\begin{array}{l} \varepsilon_r^{\mathrm{pla}}(r, t)=\varepsilon_{r, \mathrm{ve}}^{\mathrm{pla}}(r, t)+\varepsilon_{r, \mathrm{pla}}^{\mathrm{pla}}(r, t), \\ \varepsilon_\theta^{\mathrm{pla}}(r, t)=\varepsilon_{\theta, \mathrm{ve}}^{\mathrm{pla}}(r, t)+\varepsilon_{\theta, \mathrm{pla}}^{\mathrm{pla}}(r, t) . \end{array}\right. $ | (22) |
其中:εr, vepla(r, t)和εr, plapla(r, t)分别为塑性区径向应变εrpla(r, t)的黏弹性部分和塑性部分;εθ, vepla(r, t) 和εθ, plapla(r, t)分别为塑性区切向应变εθpla(r, t)的黏弹性部分和塑性部分。
塑性应变满足非关联流动法则。表示如下:
| $ \varepsilon_{r, \mathrm{pla}}^{\mathrm{pla}}(r, t)+\beta \varepsilon_{\theta, \mathrm{pla}}^{\mathrm{pla}}(r, t)=0. $ | (23) |
当切向应力为大主应力时,
| $ \beta=\frac{1+\sin \psi}{1-\sin \psi}. $ |
其中ψ为剪胀角。
由弹性-黏弹性对应原理[15]可得,开挖阶段黏弹性区的径向应力σrT1, ve(r, t)和切向应力σθT1, ve(r, t)分别表示如下:
| $ \left\{\begin{array}{l} \sigma_r^{T_1,\mathrm{v e}}(r, t)=P_0-\left[P_0-\sigma_r^{T_1, \mathrm{v e}}\left(R_{\mathrm{pla}}, t\right)\right] \frac{R_{\mathrm{pla}}^2}{r^2}, \\ \sigma_\theta^{T_1, \mathrm{v e}}(r, t)=P_0+\left[P_0-\sigma_r^{T_1, \mathrm{v e}}\left(R_{\mathrm{pla}}, t\right)\right] \frac{R_{\mathrm{pla}}^2}{r^2} . \end{array}\right. $ | (24) |
开挖阶段黏弹性区的径向位移urT1, ve(r, t)表示如下:
| $ u_r^{T_1, \text { ve }}(r, t)=\frac{\left[P_0-\sigma_r^{T_1, \text { ve }}\left(R_{\mathrm{pla}}, t\right)\right] R_{\mathrm{pla}}^2}{2 r} \int_0^t H(\tau) \mathrm{d} \tau, $ | (25) |
| $ H(t)=L^{-1}\left[\frac{1}{s \overline{G(t)}}\right] . $ | (26) |
其中:(·)表示对(·)的Laplace变换(L(·)),s为Laplace变换变量。
将式(10)和(14)联立,结合边界条件式(17),可得塑性区的应力如下:
| $ \left\{\begin{aligned} \sigma_r^{T_1, \text { pla }}(r, t)= & \frac{N}{M-1}\left[\left(\frac{r}{R_0}\right)^{M-1}-1\right], \\ \sigma_\theta^{T_1, \text { pla }}(r, t)= & M \sigma_r^{T_1, \text { pla }}(r, t)+N= \\ & \frac{M N}{M-1}\left[\left(\frac{r}{R_0}\right)^{M-1}-1\right]+N . \end{aligned}\right. $ | (27) |
将式(27)代入式(14),结合式(20)—(21),可得塑性半径:
| $ R_{\mathrm{pla}}=\left[\frac{2\left(N-P_0+M P_0\right) R_0^{M-1}}{(1+M) N}\right]^{\frac{1}{M-1}} . $ | (28) |
结合几何方程式(11)和非关联流动法则式(23)得
| $ \begin{gathered} \frac{\partial u_r^{T_1, \text { pla }}(r, t)}{\partial r}+\beta \frac{u_r^{T_1 , \text { pla }}(r, t)}{r}=g(r, t)= \\ \varepsilon_{r, \text { ve }}^{T_1, \text { pla }}(r, t)+\beta \varepsilon_{\theta, \text { ve }}^{T_1, \text { pla }}(r, t) . \end{gathered} $ | (29) |
其中εr, veT1, pla(r, t)和εθ, veT1, pla(r, t)分别为开挖阶段塑性区黏弹性径向和切向应变。
通解表示如下:
| $ u_r^{T_1, \text { pla }}(r, t)=r^{-\beta}\left[\int_{R_{\text {pla }}}^r r^\beta g(r, t) \mathrm{d} r+Q(t)\right] . $ |
结合连续性条件式(19)解得
| $ Q(t)=\frac{\left[P_0-\sigma_r^{T_1, \mathrm{ve}}\left(R_{\mathrm{pla}}, t\right)\right] R_{\mathrm{pla}}^{\beta+1}}{2} \int_0^t H(\tau) \mathrm{d} \tau . $ |
将本构方程式(12)的Laplace形式代入式(29)并进行Laplace逆变换,可得
| $ \left\{\begin{array}{l} g(r, t)=(1-\beta)\left[\sigma_r^{T_1, \text { pla }}(r, t)-\sigma_\theta^{T_1 , \text { pla }}(r, t)\right] X(t)+ \\ {\left[\begin{array}{l} -3(1+\beta) P_0+(2+\beta) \sigma_r^{T_1 , \text { pla }}(r, t)+ \\ (1+2 \beta) \sigma_\theta^{T_1, \text { pla }}(r, t) \end{array}\right] Y(t), } \\ X(t)=L^{-1}\left[\frac{1}{2(\overline{G(t)}+3 \overline{K(t)}) s^2}\right], \\ Y(t)=L^{-1}\left[\frac{3 \overline{K(t)}}{4 \overline{G(t)}(\overline{G(t)}+3 \overline{K(t)}) s^2}\right] . \end{array}\right. $ | (30) |
本文仅关注开挖引发的增量位移,以下针对增量模型(即支护后减去开挖前)进行推导。采用MC屈服准则,屈服函数的总微分可表示如下:
| $ \mathrm{d} f=\frac{\partial f}{\partial \sigma_r(r, t)} \mathrm{d} \sigma_r(r, t)+\frac{\partial f}{\partial \sigma_\theta(r, t)} \mathrm{d} \sigma_\theta(r, t)=-M \mathrm{~d} \sigma_r(r, t)+\mathrm{d} \sigma_\theta(r, t) . $ | (31) |
在支护阶段,围岩与衬砌的相互作用会产生随时间增大的支护力。与开挖阶段相比,径向应力增大,即dσr(r, t)>0;切向应力减小,即dσθ(r, t)<0。因此,可以得出df < 0,即原始塑性区发生卸载。
根据塑性理论,开挖阶段的塑形应变在卸载过程中不能恢复并保持不变。由式(22)可知,卸载区(塑性区)全时段的塑性应变变化量表示如下:
| $ \begin{gathered} \Delta \varepsilon_{r, \text { pla }}^{T_2, \text { pla }}(r, t)=\Delta \varepsilon_{r, \text { pla }}^{T_1, \text { pla }}(r, t)+ \\ {\left[\Delta \varepsilon_{r, \text { pla }}^{T_1, \text { pla }}\left(r, t_1\right)-\Delta \varepsilon_{r, \text { pla }}^{T_1, \text { pla }}(r, t)\right] U\left(t-t_1\right) ;} \end{gathered} $ | (32) |
| $ \begin{gathered} \Delta \varepsilon_{\theta, \text { pla }}^{T_2, \text { pla }}(r, t)=\Delta \varepsilon_{\theta, \text { pla }}^{T_1, \text { pla }}(r, t)+ \\ {\left[\Delta \varepsilon_{\theta, \text { pla }}^{T_1, \text { pla }}\left(r, t_1\right)-\Delta \varepsilon_{\theta, \text { pla }}^{T_1, \text { pla }}(r, t)\right] U\left(t-t_1\right) ;} \end{gathered} $ | (33) |
| $ U\left(t-t_1\right)= \begin{cases}1, & t>t_1 ; \\ 0, & t \leqslant t_1 .\end{cases} $ | (34) |
其中:Δεr, plaT1, pla(r, t1)和Δεθ, plaT1, pla(r, t1)分别为开挖阶段塑性区不可恢复的塑性径向应变变化量;Δεr, plaT2, pla(r, t1)和Δεθ, plaT2, pla(r, t1)分别为支护阶段卸载区不可恢复的塑性径向应变变化量和切向应变变化量;U(t-t1)为单位阶跃函数。
| $ \begin{gathered} \Delta \varepsilon_{r, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)=\frac{\partial \Delta u_r^{T_1 , \text { pla }}\left(r, t_1\right)}{\partial r}-\Delta \varepsilon_{r, \text { ve }}^{T_1 , \text { pla }}\left(r, t_1\right)=\frac{1}{2(M-1)(M+\beta)} r^{\beta-1} \beta \cdot \\ \left(R_{\mathrm{pla}}^\beta(M+\beta) H\left(t_1\right)\left(A_1 R_{\mathrm{pla}}^M(M-1)-R_p\left[N+(M-1) P_0\right]\right)+2 A_1 r^{M+\beta}(M-1)^2(1+M)\left(2 X\left(t_1\right)+Y\left(t_1\right)\right)-\right. \\ \left.6 R_{\mathrm{pla}}^{\beta+1}(M+\beta)\left[N+(M-1) P_0\right] X\left(t_1\right)+A_1 R_{\text {pla }}^M(M-1)\left((2+M+\beta+2 M \beta) X\left(t_1\right)+(M-1)(\beta-1) Y\left(t_1\right)\right)\right), \end{gathered} $ | (35) |
| $ \begin{gathered} \Delta \varepsilon_{\theta , \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)=\frac{\Delta u_r^{T_1 , \text { pla }}\left(r, t_1\right)}{r}-\Delta \varepsilon_{\theta , \mathrm{ve}}^{T_1 , \text { pla }}\left(r, t_1\right)=\frac{1}{2(M-1)(M+\beta)} r^{\beta-1} \cdot \\ \left(-R_{\text {pla }}^\beta(M+\beta) H\left(t_1\right)\left(A_1 R_{\text {pla }}^M(M-1)-R_p\left[N+(M-1) P_0\right]\right)-2 A_1 r^{M+\beta}(M-1)^2(1+M)\left(2 X\left(t_1\right)+Y\left(t_1\right)\right)\right. \\ \left.+6 R_{\text {pla }}^{\beta+1}(M+\beta)\left(N+(M-1) P_0\right) X\left(t_1\right)-A_1 R_{\text {pla }}^M(M-1)\left((2+M+\beta+2 M \beta) X\left(t_1\right)+(M-1)(\beta-1) Y\left(t_1\right)\right)\right), \end{gathered} $ | (36) |
| $ A_1=\frac{R_0^{1-M} N}{-1+M}. $ | (37) |
其中Δεr, veT1, pla(r, t1)和Δεθ, veT1, pla(r, t1)分别为开挖阶段塑性区黏弹性径向和切向应变变化量。
因此,卸载区应变为开挖阶段不可恢复的塑性应变与支护阶段的黏弹性应变的叠加,则
| $ \left\{\begin{array}{l} \Delta \varepsilon_r^{T_2, \text { pla }}(r, t)=\Delta \varepsilon_{r, \text { ve }}^{T_2, \text { pla }}(r, t)+\varepsilon_{r, \text { pla }}^{T_1, \text { pla }}\left(r, t_1\right), \\ \Delta \varepsilon_\theta^{T_2, \text { pla }}(r, t)=\Delta \varepsilon_{\theta, \text { ve }}^{T_2, \text { pla }}(r, t)+\varepsilon_{\theta, \text { pla }}^{T_1, \text { pla }}\left(r, t_1\right) . \end{array}\right. $ | (38) |
其中:ΔεrT2, pla(r, t)和ΔεθT2, pla(r, t)分别为支护阶段卸载区径向和切向的应变变化量;Δεr, veT2, pla(r, t)和Δεθ, veT2, pla(r, t)分别为支护阶段卸载区径向和切向的黏弹性应变变化量。
对式(38)进行Laplace变换,可得式(39)。
| $ \left\{\begin{array}{c} \overline{\Delta \varepsilon_r^{T_2, \text { pla }}(r, t)}=\overline{\Delta \varepsilon_{r, \text { ve }}^{T_2, \text { pla }}(r, t)}+ \\ \frac{\exp \left(-s t_1\right) \varepsilon_{r, \text { pla }}^{T_1, \text { pla }}\left(r, t_1\right)}{s}, \\ \overline{\Delta \varepsilon_\theta^{T_2, \text { pla }}(r, t)}=\overline{\Delta \varepsilon_{\theta, \text { ve }}^{T_2, \text { pla }}(r, t)}+ \\ \frac{\exp \left(-s t_1\right) \varepsilon_{\theta, \text { pla }}^{T_1, \text { pla }}\left(r, t_1\right)}{s}. \end{array}\right. $ | (39) |
其中:Δεθ, veT2, pla为卸载区黏弹性应变分量,Δεθ, veT2, pla满足黏弹性本构方程。
对式(11)和(12)进行Laplace变换,并与式(39)联立,得到Laplace域内塑性卸载区径向和切向应力,分别表示如下:
| $ \begin{gathered} \overline{\Delta \sigma_r^{T_2 , \text { pla }}(r, t)}-\alpha \overline{\Delta p_1(r, t)}= \\ 2 \overline{G(t)}\left[\frac{2}{3}\left(s \frac{\partial \overline{\Delta u_r^{T_2 , \text { pla }}}{\partial r}}-\exp \left(-s t_1\right) \varepsilon_{r, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)-\frac{1}{3}\left(s \overline{\frac{\Delta u_r^{T_2 , \text { pla }}}{r}}-\exp \left(-s t_1\right) \varepsilon_{\theta , \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)\right]+ \\ \overline{K(t)}\left[\left(s \frac{\partial \overline{\Delta u_r^{T_2 , \text { pla }}}{\partial r}}-\exp \left(-s t_1\right) \varepsilon_{r, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)+\left(s \frac{\overline{\Delta u_r^{T_2 , \text { pla }}}}{r}-\exp \left(-s t_1\right) \varepsilon_{\theta , \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)\right], \end{gathered} $ | (40) |
| $ \begin{gathered} \overline{\Delta \sigma_\theta^{T_2 , \text { pla }}(r, t)}-\alpha \overline{\Delta p_1(r, t)}= \\ \left.2\overline{ G(t)}\left[-\frac{1}{3}\left(s \frac{\partial \overline{\Delta u_r^{T_2 , \text { pla }}}}{\partial r}+\exp \left(-s t_1\right) \varepsilon_{r, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)+\frac{2}{3} \left(s \frac{\overline{\Delta u_r^{T_2 , \text { pla }}}}{r}\right.-\exp \left(-s t_1\right) \varepsilon_{\theta, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)\right]+ \\ \overline{K(t)}\left[\left(s \frac{\partial\overline{ \Delta u_r^{T_2 , \text { pla }}}}{\partial r}+\exp \left(-s t_1\right) \varepsilon_{r, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)+\left(s \frac{\overline{\Delta u_r^{T_2 , \text { pla }}}}{r}-\exp \left(-s t_1\right) \varepsilon_{\theta, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)\right)\right] . \end{gathered} $ | (41) |
将式(10)进行Laplace变换,
| $ \frac{\partial \overline{\Delta \sigma_r(r, t)}}{\partial r}+\frac{\overline{\Delta \sigma_r(r, t)}-\overline{\Delta \sigma_\theta(r, t)}}{r}=0 . $ | (42) |
将式(40)和(41)代入式(42),得到关于卸载区位移的微分方程,表示如下:
| $ \begin{aligned} \frac{\partial^2 \overline{\Delta u_r^{T_2 , \text { pla }}(r, t)}}{\partial r^2}+\frac{1}{r} & \cdot \frac{\partial \overline{\Delta u_r^{T_2 , \text { Pla }}(r, t)}}{\partial r}- \\ \frac{\overline{\Delta u_r^{T_2 , \text { pla }}(r, t)}}{r^2} & =h(r, s) . \end{aligned} $ | (43) |
其中:
| $ \begin{gathered} h(r, s)=\frac{\partial \varepsilon_{r, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)}{\partial r} \cdot \frac{\exp \left(-s t_1\right)}{s}+ \\ \frac{2 \overline{G(t)}}{\overline{K(t)}+\frac{4 \overline{G(t)}}{3}} \cdot \frac{1}{r} \cdot \frac{\exp \left(-s t_1\right) \varepsilon_{r , \text { pla }}^{T_1, \text { pla }}\left(r, t_1\right)}{s}+ \\ \frac{\overline{K(t)}-\frac{2 \overline{G(t)}}{3}}{\overline{K(t)}+\frac{4 \overline{G(t)}}{3}} \cdot \frac{\partial \varepsilon_{\theta, \text { pla }}^{T_1 , \text { pla }}\left(r, t_1\right)}{\partial r} \cdot \frac{\exp \left(-s t_1\right)}{s}- \\ \frac{2 \overline{G(t)}}{\overline{K(t)}+\frac{4 \overline{G(t)}}{3}} \cdot \frac{1}{r} \cdot \frac{\exp \left(-s t_1\right) \varepsilon_{\theta , \text { pla }}^{{T_1}, \text { pla }}\left(r, t_1\right)}{s}-\\ \frac{\alpha \overline{\Delta p_1(r, t)}}{\left(\frac{4}{3} \overline{G(t)}+\overline{K(t)}\right) s} . \end{gathered} $ |
微分方程式(43)的通解为
| $ \overline{\Delta u_r^{T_2 , \text { pla }}(r, t)}=D_1(s) r+\frac{D_2(s)}{r}+u_{\mathrm{par}}(s) . $ | (44) |
其中upar(s)为可求的关于s的函数,通过求解式(43)非齐次二阶偏微分方程的特解即可得到;D1(s)和D2(s)均为关于s的待定函数。边界条件和连续性条件表示如下:
| $ \Delta \sigma_r^{T_2, \text { pla }}\left(R_0, t\right)=U\left(t-t_1\right) F(t)-P_0, $ | (45) |
| $ \Delta \sigma_r^{T_2, \text { ve }}(\infty, t)=0, $ | (46) |
| $ \Delta u_r^{T_2, \text { pla }}\left(R_{\mathrm{pla}}, t\right)=\Delta u_r^{T_2, \text { ve }}\left(R_{\mathrm{pla}}, t\right), $ | (47) |
| $ \Delta \sigma_r^{T_2, \text { pla }}\left(R_{\mathrm{pla}}, t\right)=\Delta \sigma_r^{T_2, \text { ve }}\left(R_{\text {pla }}, t\right) . $ | (48) |
其中: F(t)为支护力;ΔurT2, pla(Rpla, t)和ΔurT2, ve(Rpla, t)分别为支护阶段塑性半径处卸载区和黏弹性区的径向位移;ΔσrT2, pla(Rpla, t)和ΔσrT2, ve(Rpla, t) 分别为支护阶段塑性半径处卸载区和黏弹性区的径向应力。围岩与衬砌位移协调条件表示如下:
| $ \Delta u_r^{T_2, \text { pla }}\left(R_0, t\right)-\Delta u_r^{T_1, \text { pla }}\left(R_0, t\right)=\Delta u_r^{\text {lin }}\left(R_0\right) . $ | (49) |
其中ΔurT2, pla(R0, t)-ΔurT1, pla(R0, t)为施加衬砌前后的围岩增量位移,Δurlin(R0)为衬砌位移[16]。代入各式即可求得F(t)。
将式(40)—(44)代入式(45)—(48),即可求解得D1(s)和D2(s)。先将D1(s)和D2(s)代入式(40)—(44),再将结果逆变换至时域,可获得在正确考虑加卸载路径的情况下围岩和衬砌区域内径向应力、切向应力和位移的精确解析解。因篇幅所限,在此不再具体展示详细结果。通过式(40)—(44)可以明显看出,
某隧道工程[17],P0=12.5 MPa,R0=2.6 m,R1=2.2 m,p∞=4.7 MPa,ptf=0。围岩的黏聚力c1=4.0 MPa,围岩的内摩擦角φ1=20°;衬砌的Poisson比v2=0.2,衬砌的弹性模量E2=30 GPa。围岩和衬砌的等效孔隙压力系数α皆为0.8,ψ=10°。
本文采用描述流变岩石常用的广义Kelvin模型,取GHook=2 692.31 MPa,GKelvin=769.24 MPa,KHook=5 833.33 MPa,假设ηKelvin=10 000 MPa·d。渗流场参数如下:水的黏度μwater=1×10-3 Pa·s,ϕ=0.18,Λ=5.46×10-4 MPa-1;k1=3×10-20 m2,k2=5.1×10-11 m2。
图 4给出了正确考虑加卸载路径(考虑加卸载)和未正确考虑加卸载路径(仅考虑加载)2种情况下,卸载区r=3.0 m和r=3.5 m这2个位置的位移随时间变化的情况。可以看出,正确考虑加卸载路径情况下,其位移明显大于未正确考虑的情况,即考虑应力路径影响后围岩变形会偏大,说明不可恢复的塑性应变的确会在卸载区引起额外的随时间变化的位移和应力,并且这种影响不可忽略。
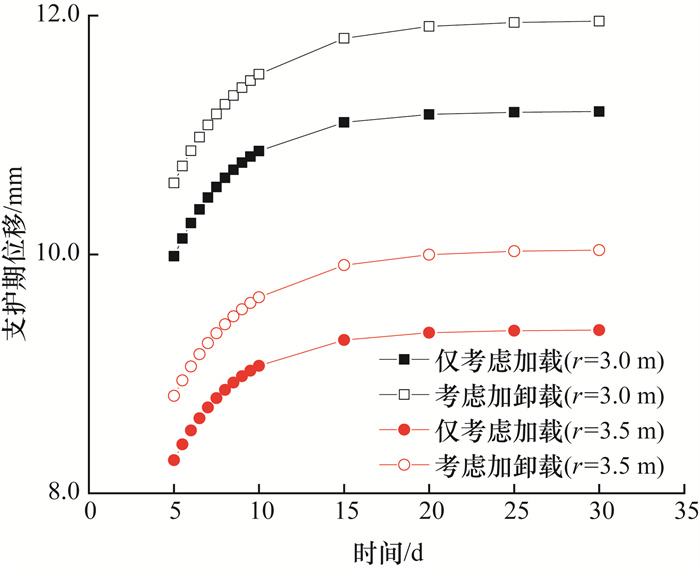
|
| 图 4 支护期2种情况的对比 |
3 结论
本文考虑了渗流影响下黏弹塑性围岩中深埋圆形衬砌隧道施工和运行全过程及其应力路径,推导了正确考虑加卸载过程的隧道开挖和支护阶段的应力、位移精确解析解。通过对比不考虑和考虑加卸载过程的位移结果,发现不考虑加卸载时的位移值偏小,容易高估围岩的稳定性。同时,该结果也说明不可恢复的塑性应变的确会在卸载区引起额外的随时间变化的位移和应力。因此,应力路径对围岩和衬砌稳定性的影响不可忽视。本文研究结果可为实际支护设计和施工流程设计提供参考。
| [1] |
孙钧. 岩石流变力学及其工程应用研究的若干进展[J]. 岩石力学与工程学报, 2007, 26(6): 1081-1106. SUN J. Rock rheological mechanics and its advance in engineering applications[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1081-1106. (in Chinese) |
| [2] |
ZHANG S L, CHENG X S, QI L, et al. Face stability analysis of large diameter shield tunnel in soft clay considering high water pressure seepage[J]. Ocean Engineering, 2022, 253: 111283. DOI:10.1016/j.oceaneng.2022.111283 |
| [3] |
余东明, 姚海林, 段建新, 等. 考虑中主应力和剪胀的深埋圆形隧道黏弹塑性蠕变解[J]. 岩石力学与工程学报, 2012, 31(S2): 3586-3592. YU D M, YAO H L, DUAN J X, et al. Viscoelastoplastic creep solutions to deep circular tunnels considering intermediate principal stress and shear dilatancy[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S2): 3586-3592. (in Chinese) |
| [4] |
KARGAR A R. An analytical solution for circular tunnels excavated in rock masses exhibiting viscous elastic-plastic behavior[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 124: 104128. DOI:10.1016/j.ijrmms.2019.104128 |
| [5] |
LIU Q S, LI J L. The viscoelastic-plastic displacement back analysis of rock mass with non-stationary parameters[J]. Advanced Materials Research, 2012, 455-456: 1538-1544. DOI:10.4028/www.scientific.net/AMR.455-456.1538 |
| [6] |
李宗利, 任青文, 王亚红. 考虑渗流场影响深埋圆形隧洞的弹塑性解[J]. 岩石力学与工程学报, 2004, 23(8): 1291-1295. LI Z L, REN Q W, WANG Y H. Elasto-plastic analytical solution of deep-buried circle tunnel considering fluid flow field[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1291-1295. (in Chinese) |
| [7] |
王华宁, 郭振宇, 高翔, 等. 含水合物地层井壁力学状态的弹塑性解析分析[J]. 同济大学学报(自然科学版), 2020, 48(12): 1696-1706. WANG H N, GUO Z Y, GAO X, et al. Elastoplastic analytical investigation of mechanical response of wellbore in methane hydrate-bearing sediments[J]. Journal of Tongji University (Natural Science), 2020, 48(12): 1696-1706. (in Chinese) |
| [8] |
王睢, 钟祖良, 刘新荣. 基于D-P屈服准则考虑渗流影响的深埋有压圆形隧洞弹塑性解[J]. 现代隧道技术, 2019, 56(1): 39-46. WANG S, ZHONG Z L, LIU X R. D-P yield criterion based elastoplastic solution for a deep-buried and pressured circular tunnel considering seepage effect[J]. Modern Tunnelling Technology, 2019, 56(1): 39-46. (in Chinese) |
| [9] |
HU T, WANG H N, JIANG M J. Analytical approach for the fast estimation of time-dependent wellbore stability during drilling in methane hydrate-bearing sediment[J]. Journal of Natural Gas Science and Engineering, 2022, 99: 104422. DOI:10.1016/j.jngse.2022.104422 |
| [10] |
EL JIRARI S, WONG H, DELERUYELLE F, et al. Analytical modelling of a tunnel accounting for elastoplastic unloading and reloading with reverse yielding and plastic flow[J]. Computers and Geotechnics, 2020, 121: 103441. DOI:10.1016/j.compgeo.2020.103441 |
| [11] |
ZHAO J D, WANG G. Unloading and reverse yielding of a finite cavity in a bounded cohesive-frictional medium[J]. Computers and Geotechnics, 2010, 37(1-2): 239-245. DOI:10.1016/j.compgeo.2009.08.002 |
| [12] |
夏才初, 徐晨, 杜时贵. 考虑应力路径的深埋隧道黏弹-塑性围岩与支护相互作用[J]. 岩石力学与工程学报, 2021, 40(9): 1789-1802. XIA C C, XU C, DU S G. Interaction between viscoelastic-plastic surrounding rock and support structure in deep tunnels considering stress path[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(9): 1789-1802. (in Chinese) |
| [13] |
XU C, XIA C C, DU S G. Simplified solution for viscoelastic-plastic interaction between tunnel support and surrounding rock based on MC and GZZ strength criteria[J]. Computers and Geotechnics, 2021, 139: 104393. DOI:10.1016/j.compgeo.2021.104393 |
| [14] |
HUANG J J, JIANG M J, WANG H N. An analytical model of time-dependent elastoplasticity with hydraulic-mechanical coupling for wellbore stability in hydrate exploitation[J]. Marine Georesources & Geotechnology, 2023, 41(12): 1354-1369. |
| [15] |
WANG H N, UTILI S, JIANG M J, et al. Analytical solutions for tunnels of elliptical cross-section in rheological rock accounting for sequential excavation[J]. Rock Mechanics and Rock Engineering, 2015, 48(5): 1997-2029. DOI:10.1007/s00603-014-0685-7 |
| [16] |
付睿聪, 王华宁, 蒋明镜, 等. 考虑加卸载路径的深埋水工隧道弹塑性解析解[J]. 岩石力学与工程学报, 2021, 40(S2): 3174-3181. FU R C, WANG H N, JIANG M J, et al. Elastoplastic solution of deep hydraulic tunnel considering loading and unloading paths[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(S2): 3174-3181. (in Chinese) |
| [17] |
MÁNICA M A, GENS A, VAUNAT J, et al. Numerical simulation of underground excavations in an indurated clay using non-local regularisation. Part 1: Formulation and base case[J]. Geotechnique, 2022, 72(12): 1092-1112. DOI:10.1680/jgeot.20.P.246 |



