2. 北京航天自动控制研究所 宇航智能控制技术全国重点实验室, 北京 100854
2. National Key Laboratory of Science and Technology on Aerospace Intelligence Control, Beijing Aerospace Automatic Control Institute, Beijing 100854, China
近年来,低轨巨型星座技术飞速发展。2015年美国SpaceX公司公布的“星链”计划预计发射41 927颗低轨卫星,截至2023年9月,已发射5 200多颗[1]。随着低轨巨型星座卫星在轨数量不断增加,以低轨卫星为光学信息源的光学导航技术的可应用性不断提高。当光学视场内同时观测到3颗及以上卫星时,可利用n点透视(perspective-n-point, PnP)问题进行位姿解算。PnP问题最早用于相机标定,后来拓展至视觉SLAM(simultaneous localization and mapping)、空间非合作目标位姿估计等工程任务[2-8]。以上应用场景中,定位点与目标点的相对距离均在米至百米级,而对定位点(本文以舰船为例)与目标卫星相对距离在100 km以上的空间几何定位问题讨论很少。
本文假设待观测的低轨目标卫星轨道高度为500~600 km,定位点固连于舰船上。不失一般性,本文仅讨论视场内3颗卫星同时可见的情形,利用P3P(PnP, n=3)算法实现位置解算。由于定位点与目标点距离较远,部分情况接近奇异,因此图像噪声对定位精度的影响较大,传统PnP算法难以满足定位精度要求。
在卫星导航领域,为提高定位精度从可见卫星中选择4个构型关系最佳卫星的进行导航定位。精度因子(dilution of precision, DOP)[9]是用卫星构型的几何性质表征卫星定位精度的物理量,其包含多种类型[10]。其中位置精度因子(position DOP,PDOP)是目前衡量卫星几何构型的常用方法,但该方法未考虑相机与目标卫星的距离信息,不能全面表征星座构型。
由于用P3P算法解析求解时含有复杂的三角函数运算,难以按照PDOP原理推导出误差表达式。因此,本文参考文[11-18]的分析思路,基于统计学思想,结合PDOP对卫星几何构型的评判方法,通过研究星座几何构型对定位误差的影响,建立星座几何构型评价函数,从几何构型和评价函数角度优选良好构型的观测数据进行定位解算,提高远距离目标的定位精度。
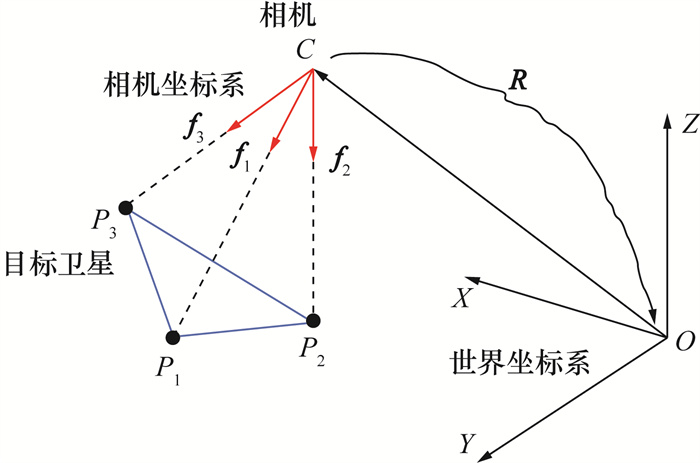
1 算法原理 1.1 定位原理Kneip算法[19]是一种闭合解的P3P求解方式,具有求解稳定、速度快的优点。该算法通过引入相机和世界坐标系的中间坐标系,计算相机中间坐标系和世界中间坐标系之间的相对姿态和位置,求解相机的位姿,如图 1所示。其中:C为相机(镜头)中心点;P1、P2、P3为目标卫星;给定P1、P2、P3的位置坐标和视线矢量f1、f2、f3,可求出相机相对于世界坐标系的C和R,具体步骤如下。
|
| 图 1 P3P问题图解 |
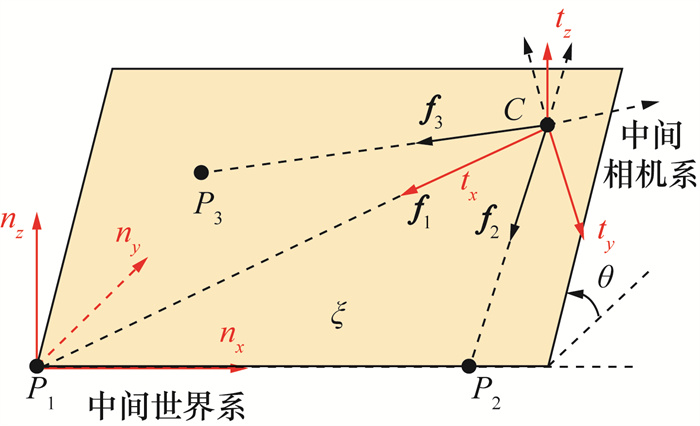
建立相机和世界坐标系的中间坐标系,如图 2所示,建立半平面ξ推导二者的变换关系,将P3P问题转化为一个四阶多项式的求解问题,表示如下:
|
| 图 2 中间相机系和中间世界系 |
| $ a_0+a_1 \cos \theta+a_2 \cos ^2 \theta+a_3 \cos ^3 \theta+a_4 \cos ^4 \theta=0 . $ | (1) |
其中:θ为C、P1和P2构成的平面与中间世界系xoy平面的夹角;ai(i=0, 1, 2, 3, 4)为多项式的系数,由卫星的视线矢量、实际位置等已知参数变换组成。求解出θ即可得到相机相对于世界坐标系的C和R。
1.2 PDOP解算模型在GPS伪距绝对定位中,卫星几何分布对定位精度的影响通过DOP反映。测码伪距的观测方程有4个未知参数,即x、y、z和Δtu(3个位置坐标分量和1个钟差参数)。对于4颗卫星可见工况而言,测码伪距ρi可表示为
| $ \begin{gathered} \rho_i=\left[\left(x-x_{\mathrm{a}_i}\right)^2+\left(y-y_{\mathrm{a}_i}\right)^2+\left(z-z_{\mathrm{a}_i}\right)^2\right]^{\frac{1}{2}}+c \Delta t_{\mathrm{u}}, \\ i=1, 2, 3, 4 . \end{gathered} $ | (2) |
其中:c为电磁波波速,即光速3×108 m/s;xai、yai和zai分别为第i个卫星的位置坐标分量。式(2)经线性化处理后,系数矩阵Gu表示为
| $ \boldsymbol{G}_{\mathrm{u}}=\left[\begin{array}{llll} -p_{11} & -p_{12} & -p_{13} & 1 \\ -p_{21} & -p_{22} & -p_{23} & 1 \\ -p_{31} & -p_{32} & -p_{33} & 1 \\ -p_{41} & -p_{42} & -p_{43} & 1 \end{array}\right]. $ | (3) |
DOP矩阵G可表示为
| $ \boldsymbol{G}=\left(\boldsymbol{G}_{\mathrm{u}}^{\mathrm{T}} \boldsymbol{G}_{\mathrm{u}}\right)^{-1} . $ | (4) |
参考卫星导航中的DOP定义,对于本文P3P算法而言,由于相机作为量测传感器不涉及信号传播,也不包含时间信息,因此观测方程可改写为
| $ \begin{gathered} \rho_i=\left[\left(x-x_{\mathrm{a}_i}\right)^2+\left(y-y_{\mathrm{a}_i}\right)^2+\left(z-z_{\mathrm{a}_i}\right)^2\right]^{\frac{1}{2}}, \\ i=1, 2, 3 . \end{gathered} $ | (5) |
相应系数矩阵Gu为
| $ \boldsymbol{G}_{\mathrm{u}}=\left[\begin{array}{lll} -h_{11} & -h_{12} & -h_{13} \\ -h_{21} & -h_{22} & -h_{23} \\ -h_{31} & -h_{32} & -h_{33} \end{array}\right] \text {. } $ | (6) |
其中(hi1, hi2, hi3)为相机至卫星i的方向余弦。由式(4)可得DOP矩阵G为
| $ \boldsymbol{G}=\left[\begin{array}{lll} g_{11} & g_{12} & g_{13} \\ g_{21} & g_{22} & g_{23} \\ g_{31} & g_{32} & g_{33} \end{array}\right] . $ | (7) |
PDOP为矩阵G的迹,即
| $ \mathrm{PDOP}=\operatorname{tr}(\boldsymbol{G})=\sqrt{g_{11}+g_{22}+g_{33}} . $ | (8) |
PDOP与定位误差呈负相关,在P3P算法几何构型的研究中,PDOP在一定程度上也能表征四面体构型的优劣。但PDOP中利用的是空间矢量的方向信息,不能表征距离信息。
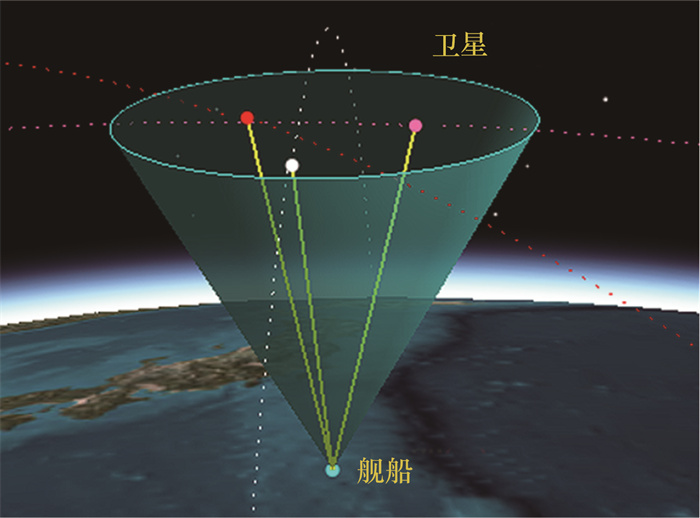
2 星座构型对定位误差的影响本文为提高P3P定位精度,利用Monte Carlo仿真研究视场内可见目标卫星与定位点的几何构型对定位误差的影响,优选量测信息源。研究中假设待定位相机固连于舰船上,待观测卫星轨道高度分布在500~600 km。鉴于相机视场越大,几何构型表征可视性越强,本节相机分辨率设定为1 024 ×1 024 pixels、视场为60°×60°,如图 3所示。不失一般性,像平面添加均值为0.040 pixels、方差为0.004 pixels的Gaussian噪声。
|
| 图 3 仿真场景模拟示意图 |
卫星几何构型表征指标可分为二维信息(像平面)和三维信息(包括卫星距离),本节分别讨论平面几何构型和观测距离对定位误差的影响。
2.1 卫星平面分布为独立分析各几何构型因素对定位误差的影响,设置星座卫星位于相同的轨道高度,仅研究卫星平面分布下几何构型对定位误差的影响。
2.1.1 图像中三角形面积在定位点与目标点轨道高度距离一定的情况下,3个目标点分布越分散,形成的三角形面积越大,其几何构型越好。
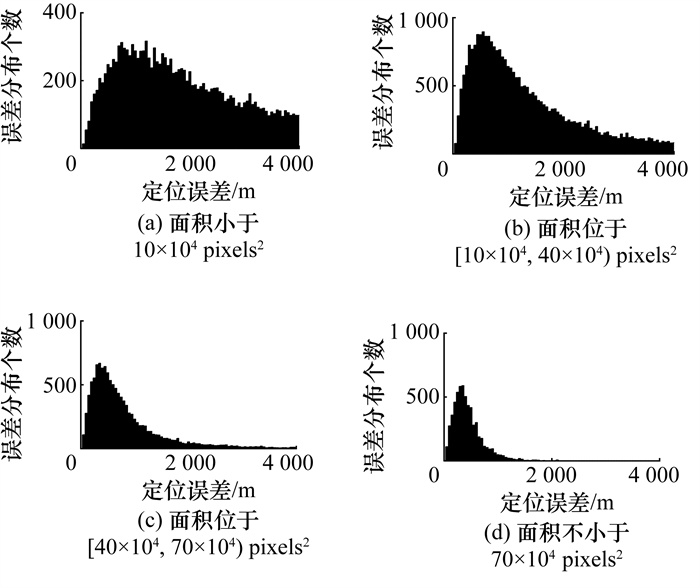
如图 4所示,当三角形面积小于10×104 pixels2时,定位误差较大,分布较分散;当三角形面积不小于70×104 pixels2时,定位误差主要集中在小于1 000 m区间内。但4个面积区间中在定位误差小于1 000 m的区间内均存在峰值,这说明图像中三角形面积并不是影响几何构型和定位误差的唯一因素,而是与其他因素耦合,共同影响几何构型和定位精度。
|
| 图 4 三角形面积与定位误差分布关系 |
2.1.2 星座三角形内角角度差
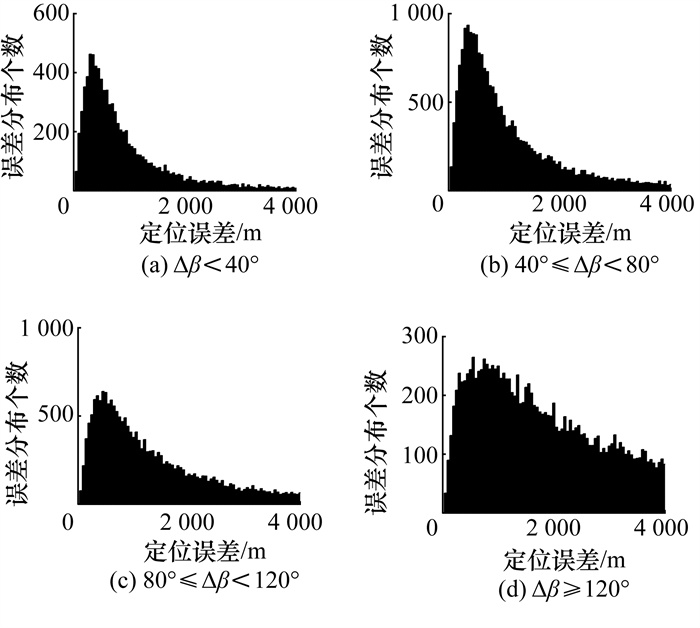
星座三角形的角度在一定程度上反映三角形的形状、3个星点的分布和四面体构型。本文经过多次统计与分析,得到不同角度差范围下定位误差的分布情况,如图 5所示。当三角形最大角与最小角的角度差Δβ≥120°时,定位误差分布较分散,大于1 000 m的占比较多;当Δβ<40°时,定位误差集中在小于1 000 m的区间内,并存在明显的峰值。因此,Δβ也是影响定位精度的因素之一。
|
| 图 5 Δβ与定位误差分布关系 |
2.2 卫星轨道高度
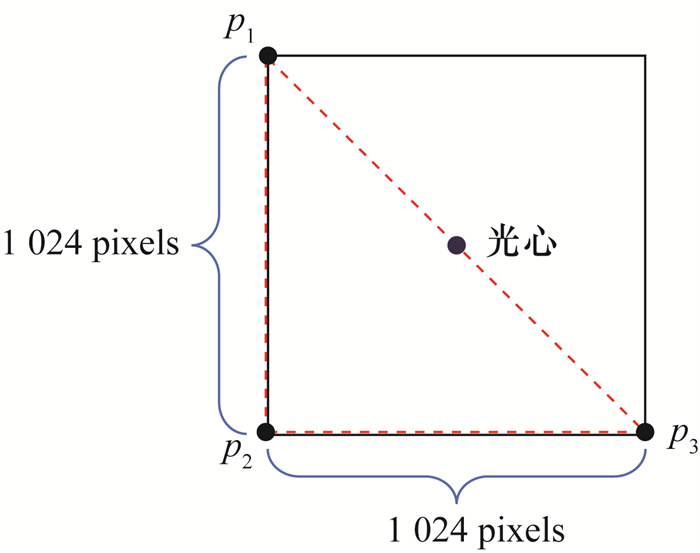
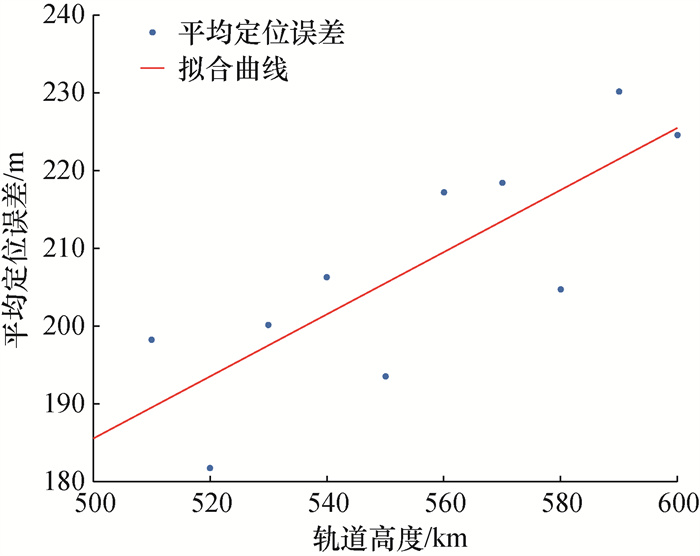
以图 6像平面中点P1、P2和P3构成的等腰三角形为例,研究卫星轨道高度从500 km至600 km变化时(步长为5 km)对定位误差的影响。如图 7所示,在相机固定情况下,卫星轨道越高,定位误差越大。从几何角度来看,在相机与卫星构成的四面体顶角及3条侧棱指向一定时,四面体的侧棱长度与定位精度呈负相关。
|
| 图 6 卫星星点像平面分布 |
|
| 图 7 卫星轨道高度与定位误差的关系 |
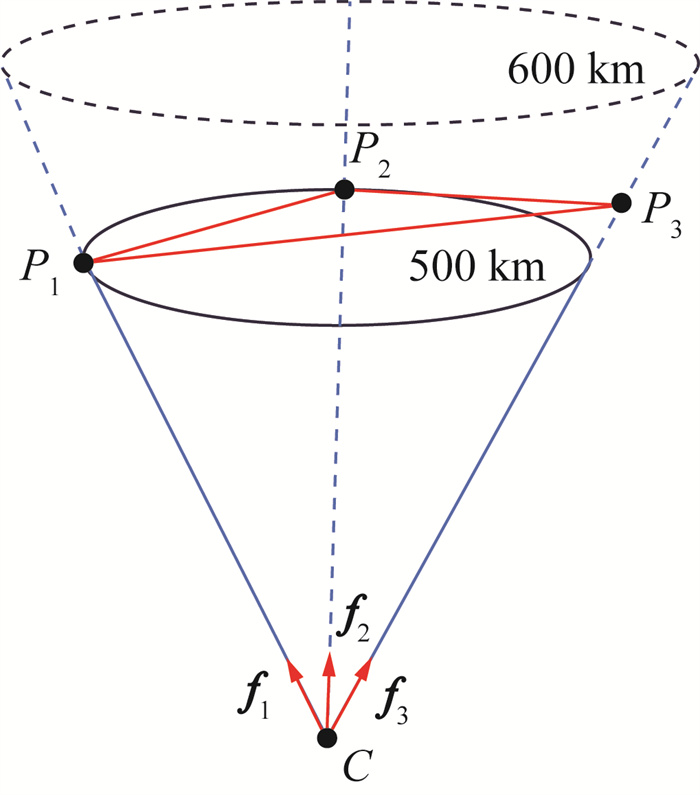
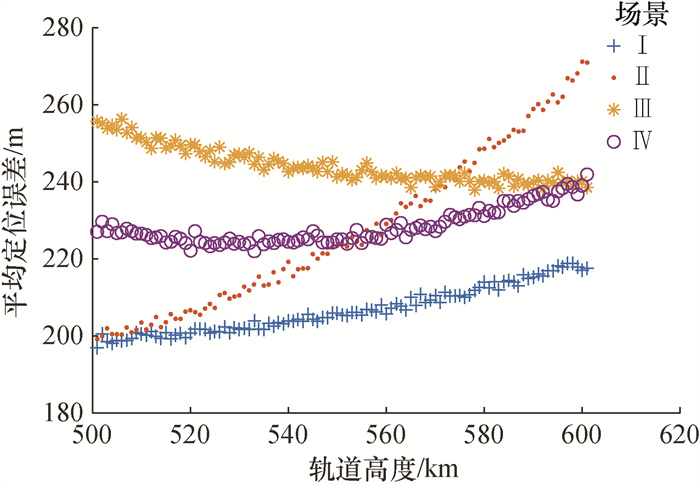
仅改变四面体中一条侧棱的长度,研究定位误差的分布。仍以图 6像平面等腰三角形为基准,图 8为固定2颗卫星高度,另一颗卫星沿视线矢量方向移动以改变侧棱长度。图 9为3颗卫星像平面投影相同、不同高度下定位误差分布情况。表 1为图 9中4类场景对应的卫星高度分布情况。
|
| 图 8 P3P中一个顶点变动的四面体构型 |
|
| 图 9 不同构型的定位误差分布 |
| km | |||||||||||||||||||||||||||||
| 场景 | P1 | P2 | P3 | ||||||||||||||||||||||||||
| Ⅰ | 500 | 500 | 500~600 | ||||||||||||||||||||||||||
| Ⅱ | 500 | 500~600 | 500 | ||||||||||||||||||||||||||
| Ⅲ | 550 | 600 | 500~600 | ||||||||||||||||||||||||||
| Ⅳ | 550 | 500~600 | 600 | ||||||||||||||||||||||||||
以场景Ⅰ为例,P1、P2高度均固定为500 km,P3高度从500 km至600 km变化, 由图 9可知,随着P3高度增加,定位误差增大;而场景Ⅱ中P1、P3高度均固定为500 km,P2高度从500 km至600 km变化,其变化曲线位于场景Ⅰ上方。因此,对于同一组视线矢量构成的构型而言,不同侧棱长度变化对定位误差的影响不同,研究平面构型时,应考虑卫星距离对构型的影响。
2.3 PDOP与定位误差分布的关系本文参考卫星导航PDOP概念描述星座卫星相对于相机的分布情况。表 2列出了PDOP与定位误差的关系,PDOP越小,定位误差小于1 000 m的比例越大。当PDOP < 5时,定位误差并非都较小,因为PDOP未考虑卫星轨道分布高度(距离信息)的影响,这说明本文工况下仅用PDOP评价几何构型不够准确。
| PDOP | 数量/个 | 总数/个 | 小于1 000 m占比/% |
| < 5 | 11 674 | 15 471 | 75.46 |
| 5~12 | 9 613 | 21 704 | 44.29 |
| >12 | 16 180 | 42 825 | 33.78 |
3 改进定位算法
提取影响几何构型的指标参数,建立评价函数,对几何构型的可用度进行分析。
根据第2章分析结果,选取影响几何构型的指标参数,分别为角度指标Δβ、面积指标M(三角形面积)和距离指标I(3个卫星与相机的距离比作差的求和值)。其中,选择I是为了抵消各指标数值量级的相互影响,并表征星座距离信息对构型的影响。另外,I也是PDOP无法表征的。I确定后,采用熵权法计算各参数权重,把各待评价单元信息进行量化与综合,对各参数进行赋权。
基于熵权法对Δβ进行无量纲化处理,该指标与定位误差呈负相关。定义Δβ为负向指标,无量纲化表示如下:
| $ \left\{\begin{array}{l} \Theta_i=\frac{180^{\circ}-\Delta \beta_i}{180^{\circ}}, \\ \boldsymbol{\Theta}=\left[\Theta_i\right]_{n \times 1} . \end{array}\right. $ | (9) |
其中:Θi为无量纲化后3个星点构成三角形的Δβ;Θ为由Θi组成的矩阵;i为总数据组数;n为总数据数。
对M进行无量纲化处理,表示如下:
| $ \left\{\begin{array}{l} S_i=\frac{2 M_i}{l h}, \\ \boldsymbol{S}=\left[S_i\right]_{n \times 1} . \end{array}\right. $ | (10) |
其中:Si为第i个无量纲化后3个星点构成的三角形面积;S为所有Si数据构成的矩阵;l为星图水平分辨率;h为星图垂直分辨率。
选取3颗卫星与相机的距离d1、d2和d3间的距离比k1、k2和k3衡量四面体空间构型指标,对其进行无量纲化处理,表示如下:
| $ \left\{\begin{array}{l} k_i=\frac{d_i}{d_1}, \quad i=1, 2, 3 ; \\ I_i=\left|k_1-k_2\right|+\left|k_1-k_3\right|+\left|k_2-k_3\right| ; \\ \boldsymbol{I}=\left[I_i\right]_{n \times 1} . \end{array}\right. $ | (11) |
其中:Ii为3个距离比互相作差的求和值;I为所有处理后的Ii数据构成的矩阵。
卫星与相机的距离为未知量,需要舰船提供先验信息。本文首先假设惯导系统提供带有误差的初始位置[Lat', Lon', Alt']T,可得到粗略距离值d1、d2和d3。将无量纲的数据组成矩阵A,表示如下:
| $ \begin{gathered} \boldsymbol{A}=\left[\begin{array}{ll} \boldsymbol{\Theta} & \boldsymbol{S} \quad \boldsymbol{I} \end{array}\right]=\left[X_{i j}^{\prime}\right]_{n \times m}, \\ i=1, 2, \cdots, n, j=1, 2, \cdots, m . \end{gathered} $ | (12) |
其次,计算A中第i组数据第j列参数值与第j列所有参数求和值的比值Yij,表示如下:
| $ Y_{i j}=\frac{X_{i j}^{\prime}}{\sum\limits_{i=1}^n X_{i j}^{\prime}}, \quad 0<Y_{i j} \leqslant 1 . $ | (13) |
再次,计算第j列参数的熵值ej,表示如下:
| $ e_j=\sum\limits_{i=1}^n \frac{Y_{i j} \ln \left(Y_{i j}\right)}{-\ln (n)}. $ | (14) |
最后,计算各参数对应的综合权重wj,表示如下:
| $ w_j=\frac{1-e_j}{\sum\limits_{j=1}^m\left(1-e_j\right)} . $ | (15) |
将得到的各参数对应权重代入式(16)得到评价函数。
| $ Q_i=\sum\limits_{j=1}^m w_{i j} X_{i j}^{\prime}. $ | (16) |
其中Qi为熵权法中不同指标无量纲化后加权得到的值。
计算出Δβ、M和I的权重,建立评价函数,获得基于不同定位误差下几何构型的可用度分布,确定构型筛选的标准。
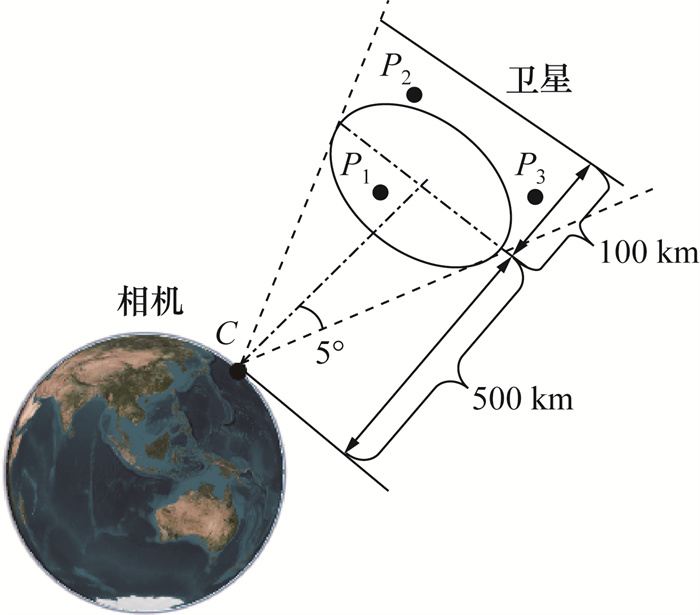
4 仿真校验与分析考虑当前主流相机视场角多为10°,本章仿真中设置相机视场为10°×10°、分辨率为1 024×1 024 pixels,如图 10所示。不失一般性,模拟星图像平面添加0.100 pixels的均值噪声。仿真中假设舰船惯导系统提供误差约2 km的初始位置。低速行驶的舰船在单次定位期间按静止不动处理,当已知3颗合作卫星的绝对空间坐标及其像平面二维坐标时,通过式(17)计算合作卫星与相机间的视线矢量fi,便可利用P3P-Kneip算法进行位置求解。需要说明的是,相机视场内3颗卫星并非必须隶属于同一星座,即使不同星座的3颗卫星,只要获取了卫星的图像坐标和实际位置,便可应用基于构型筛选的P3P方法进行定位。
|
| 图 10 仿真场景示意图 |
| $ \boldsymbol{f}_i=\left[\begin{array}{lll} \frac{u_i}{F} & \frac{v_i}{F} & 1 \end{array}\right]^{\mathrm{T}}, \quad i=1, 2, 3 . $ | (17) |
其中:(ui, vi)为卫星的图像坐标;F为相机焦距。
将单次拍摄星图中的星点提取后,利用熵权法计算出3个参数的权重为w =[0.22, 0.6, 0.18]T,得到的评价函数为
| $ Q=0.22 \boldsymbol{\Theta}+0.6 \boldsymbol{S}+0.18 \boldsymbol{I} . $ | (18) |
其中Q为可用度,表示该组数据是否可用于定位。
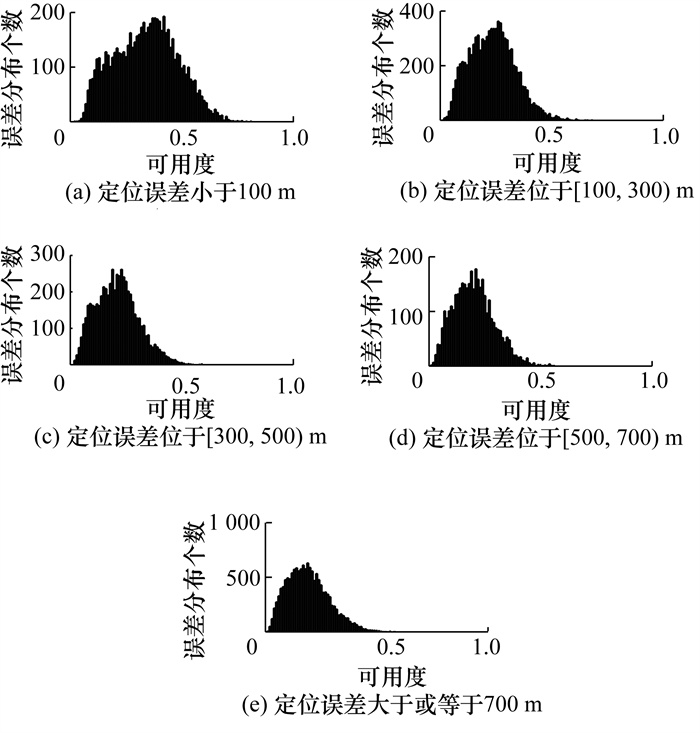
图 11为进行4万次Monte Carlo仿真的可用度分布情况。综合图 11中4万组数据,可用度大于0.4的数据主要集中在图 11a和11b中,对应的定位误差小于300 m,图 11e中可用度主要分布在小于0.4的区间,对应的定位误差不小于700 m。定位误差不小于700 m的可用度主要集中在0.4以内;定位误差小于300 m的可用度主要集中在0.4以上。定位误差越大,Q取值小的比例越大。因此,选取Q值最大的卫星观测数据进行定位。
|
| 图 11 可用度分布 |
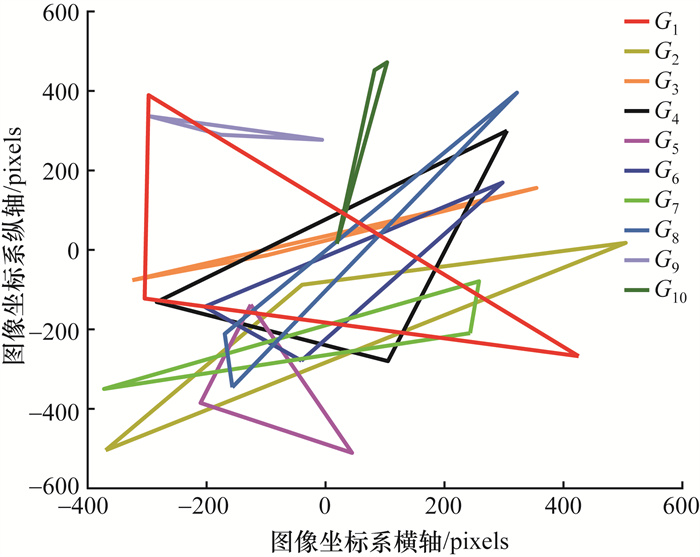
随机生成10组观测数据G1—G10进行验证,10种像平面投影如图 12所示。利用本文构型评价方法从10组观测数据中选择Q值最大的一组,同时利用PDOP筛选方法选择PDOP值最小的一组。发现2种方法筛选出同一组构型G1。这组卫星像素点分布最分散,像平面投影面积最大,符合本文评价方法的原则。10组观测数据进行P3P-Kneip算法定位的平均误差为393.5 m,而利用筛选出的最优构型解算的定位误差仅为93.4 m,验证了改进算法的有效性。
|
| 图 12 10种构型像平面投影分布图 |
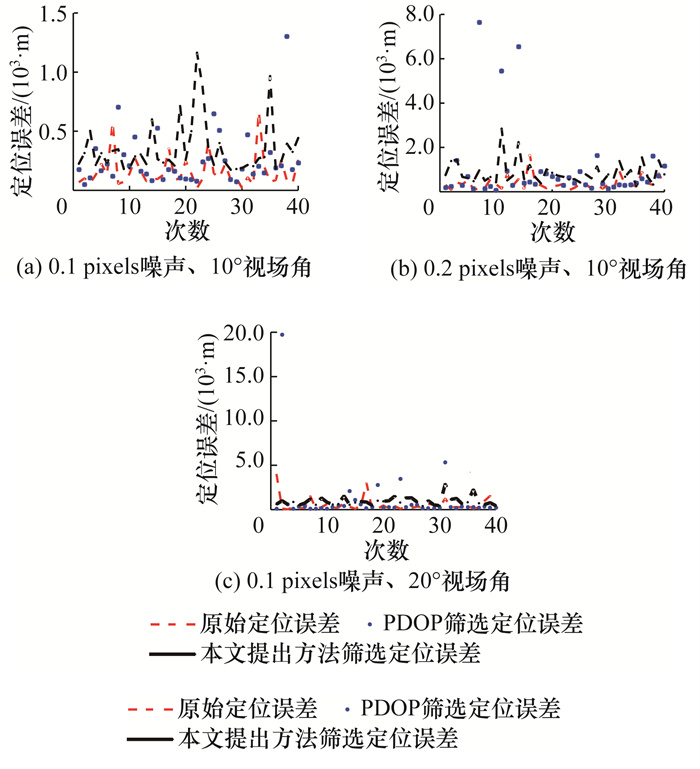
为验证改进算法的鲁棒性,进行40次模拟定位,每次拍摄1张星图,仿真中添加0.100 pixels的均值星图噪声,设置1张星图中有8颗卫星可作为定位数据源,选取其中3颗进行P3P-Kneip定位。构型优选后利用P3P-Kneip算法对单次观测数据进行定位解算,平均定位误差为185.4 m。利用PDOP筛选得到的最终平均定位误差为297.3 m;利用P3P-Kneip算法对原始观测数据进行定位解算的平均定位误差为384.9 m。40次定位误差分布如图 13a所示;添加0.200 pixels的均值噪声,定位误差分布如图 13b所示;改变相机视场角参数,添加0.100 pixels的均值噪声,定位误差分布如图 13c所示。这3种算法的平均定位误差如表 3所示,本文构型筛选算法的定位精度最高,更换光学相机后仍适用。在CPU主频为1.9 GHz的笔记本电脑上:本文构型筛选方法计算耗时0.060 s;PDOP筛选方法耗时0.020 s;未经筛选PnP定位方法平均耗时0.016 s。毫秒级解算时间可用于舰船行驶中的定位。
|
| 图 13 定位误差仿真结果 |
| 图像噪声 pixels |
视场角 (°) |
定位误差/m | ||
| 原始方法 | PDOP筛选 方法 |
本文方法 | ||
| 0.100 | 10 | 384.9 | 297.3 | 185.4 |
| 0.200 | 10 | 768.8 | 491.0 | 309.2 |
| 0.100 | 20 | 876.5 | 633.4 | 576.3 |
由表 3可知:当相机分辨率和添加噪声相同时,增大相机视场角,单位像素对应的实际尺寸增加,导致定位误差增大。因此,导航定位时相机参数选择同样重要。
表 4为表 3数据的扩展,在相机视场均为10°时,构型优选后的定位精度较无构型筛选提高约50%,表明在远距离几何定位中,多颗卫星几何构型对定位精度的影响较大。相较于PDOP筛选方法,本文构型评价算法增加了对卫星高度信息的考量。从定位结果来看,本文构型筛选方法较PDOP优选的构型定位精度提高约37%。因此,针对远距离几何定位问题,利用本文构型评价算法评价目标源的几何构型更合理。
| 图像噪声 pixels |
视场角 (°) |
定位精度提高/% | |
| 较原始方法 | 较PDOP方法 | ||
| 0.100 | 10 | 51.84 | 37.64 |
| 0.200 | 10 | 58.78 | 37.03 |
| 0.100 | 20 | 34.25 | 9.01 |
5 结论
本文提出一种基于星座构型筛选的改进几何定位方法,综合考虑星座卫星的平面分布和距离分布,选取Δβ、M和I等相关参数,建立评价函数用于构型优选。仿真结果显示: 3颗卫星分布面积越大、越分散,定位误差越小。构型筛选P3P-Kneip方法定位精度较原始情况提升超过50%,有效提高了远距离情况下纯P3P几何定位的精度。本文将卫星高度信息纳入几何构型的评价指标,改善了PDOP在远距离几何定位构型评价中的局限性,构型筛选P3P-Kneip方法较PDOP筛选下定位精度提高约37%。星座卫星丰富了空间导航信息源,本文提出的通过构型筛选改进的P3P方法可为远距离光学导航定位提供参考。
| [1] |
王勇, 龙定央, 骆盛, 等. "星链"系统星座覆盖及应用分析[J]. 中国航天, 2021(8): 43-47. WANG Y, LONG D Y, LUO S, et al. Constellation coverage and application analysis of Starlink system[J]. Aerospace China, 2021(8): 43-47. (in Chinese) |
| [2] |
PUMAROLA A, VAKHITOV A, AGUDO A, et al. PL-SLAM: Real-time monocular visual SLAM with points and lines [C]//IEEE International Conference on Robotics and Automation. Singapore, Singapore: IEEE, 2017: 4503-4508.
|
| [3] |
MARCHAND E, UCHIYAMA H, SPINDLER F. Pose estimation for augmented reality: A hands-on survey[J]. IEEE Transactions on Visualization and Computer Graphics, 2016, 22(12): 2633-2651. DOI:10.1109/TVCG.2015.2513408 |
| [4] |
XU J J, SONG B, YANG X, et al. An improved deep keypoint detection network for space targets pose estimation[J]. Remote Sensing, 2020, 12(23): 3857. DOI:10.3390/rs12233857 |
| [5] |
汪启跃, 王中宇. 基于单目视觉的航天器位姿测量[J]. 应用光学, 2017, 38(2): 250-255. WANG Q Y, WANG Z Y. Position and pose measurement of spacecraft based on monocular vision[J]. Journal of Applied Optics, 2017, 38(2): 250-255. (in Chinese) |
| [6] |
LIU H Q, GUAN X J, LUO S B, et al. Vision inertial fusion based on BP neural network for aircraft autonomous positioning [C]//2020 International Conference on Guidance, Navigation and Control. Tianjin, China: Springer, 2020: 2905-2915.
|
| [7] |
JOSPIN L, STOVEN-DUBOIS A, CUCCI D A. Photometric long-range positioning of LED targets for cooperative navigation in UAVs[J]. Drones, 2019, 3(3): 69. DOI:10.3390/drones3030069 |
| [8] |
刘崇亮, 刘垒, 扈光锋, 等. 一种着陆视觉导航P3P问题的解法[J]. 导航定位与授时, 2018, 5(1): 64-67. LIU C L, LIU L, HU G F, et al. A P3P problem solving algorithm for landing vision navigation[J]. Navigation Positioning and Timing, 2018, 5(1): 64-67. (in Chinese) |
| [9] |
刘建业. 导航系统理论与应用[M]. 西安: 西北工业大学出版社, 2010. LIU J Y. Theory and application of navigation system[M]. Xi'an: Northwestern Polytechnical University Press, 2010. (in Chinese) |
| [10] |
ANSARI K, JAMJAREEGULGARN P. Effect of weighted PDOP on performance of linear Kalman filter for RTK drone data[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-4. |
| [11] |
朱林梅, 董秀成, 张征宇, 等. 面向奇异构型目标点分布的相机位姿估计算法[J]. 光子学报, 2021, 50(7): 293-305. ZHU L M, DONG X C, ZHANG Z Y, et al. Camera pose estimation algorithm for singular configuration of target points[J]. Acta Photonica Sinica, 2021, 50(7): 293-305. (in Chinese) |
| [12] |
洪洋, 孙秀霞, 王栋, 等. 基于矩形几何特性的小型无人机快速位姿估计方法[J]. 中国激光, 2016, 43(5): 226-238. HONG Y, SUN X X, WANG D, et al. Fast pose estimation method for unmanned aerial vehicle based on rectangular geometry feature[J]. Chinese Journal of Lasers, 2016, 43(5): 226-238. (in Chinese) |
| [13] |
王中宇, 李亚茹, 郝仁杰, 等. 基于点特征的单目视觉位姿测量算法[J]. 红外与激光工程, 2019, 48(5): 169-176. WANG Z Y, LI Y R, HAO R J, et al. Monocular vision pose measurement algorithm based on points feature[J]. Infrared and Laser Engineering, 2019, 48(5): 169-176. (in Chinese) |
| [14] |
CHRISTIAN J A. Autonomous initial orbit determination with optical observations of unknown planetary landmarks[J]. Journal of Spacecraft and Rockets, 2019, 56(1): 211-220. |
| [15] |
黄西尧, 何羿霆, 杜华军, 等. 地球同步轨道目标物深度学习检测方法[J]. 宇航学报, 2021, 42(10): 1283-1292. HUANG X Y, HE Y T, DU H J, et al. Geostationary orbit object detection based on deep learning[J]. Journal of Astronautics, 2021, 42(10): 1283-1292. (in Chinese) |
| [16] |
黎奇, 白征东, 黎琼, 等. 定位测姿系统室外三维动态检定场的几何设计[J]. 清华大学学报(自然科学版), 2019, 59(11): 895-901. LI Q, BAI Z D, LI Q, et al. Geometric design of an outdoor three-dimensional kinematic verification field for a position and orientation system[J]. Journal of Tsinghua University (Science and Technology), 2019, 59(11): 895-901. (in Chinese) |
| [17] |
KIM Y, LEE D J, BANG H. Vision-only terrain referenced navigation and uncertainty analysis for unmanned aircraft [C]//AIAA Guidance, Navigation, and Control (GNC) Conference. Boston, USA: AIAA, 2013: 4696-4706.
|
| [18] |
高扬, 王梦丽, 楚恒林. 卫星导航信号畸变模型威胁空间减小方法[J]. 清华大学学报(自然科学版), 2021, 61(9): 1008-1014. GAO Y, WANG M L, CHU H L. Threat space reduction method for satellite navigation signal distortion model[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(9): 1008-1014. (in Chinese) |
| [19] |
KNEIP L, SCARAMUZZA D, SIEGWART R. A novel parametrization of the perspective-three-point problem for A direct computation of absolute camera position and orientation [C]//IEEE CVPR 2011. Colorado Springs, USA: IEEE, 2011: 2969-2976.
|



