2. 中国水利水电科学研究院 水资源研究所, 北京 100044
2. Department of Water Resources Research, China Institute of Water Resources and Hydropower Research, Beijing 100044, China
管道系统颗粒水力输送是一种成本低廉、易于实现、环境友好且被广泛使用的物料输送方式[1]。管内颗粒两相流动复杂且流型多样,涉及各种复杂的物理现象,如颗粒聚集、碰撞和破碎及管道堵塞、磨损甚至击穿[2-6]。因此,对管道系统颗粒水力输送特性展开深入研究,对矿物和化工等输送系统的设计、可靠运行及后期维护有重要指导意义。
数值研究已成为多相流理论发展和工程应用中的一种常用手段,具有方便快捷和成本低的优点。两相流数值方法可分为连续介质法和离散元法(discrete element method,DEM)。前者计算量相对小,被广泛应用于颗粒体积浓度较高和颗粒较为均匀的问题中,但无法获取每个颗粒详尽的运动和碰撞信息。而DEM在Lagrange框架下捕捉每个颗粒的运动和碰撞信息,很好地考虑了非球形颗粒、级配颗粒和颗粒-颗粒/流体间相互作用的影响。DEM与计算流体动力学(computational fluid dynamics,CFD)耦合的CFD-DEM方法已被广泛用于复杂流体-颗粒两相流研究。
CFD-DEM模型根据是否精确解析颗粒界面流动可分为解析CFD-DEM模型和非解析CFD-DEM模型。解析CFD-DEM模型能够精确解析颗粒表面流动,求解精度高,但需要极其精细的网格(流体网格尺度约为颗粒尺度的1/10~1/8),无法应用于颗粒数巨大的工程领域。而非解析CFD-DEM模型无需精细求解颗粒表面的流动,根据各种力模型计算颗粒所受的作用力,根据颗粒运动方程更新颗粒运动状态。非解析CFD-DEM模型通常基于Reynolds-Averaged Navier-Stokes(RANS)方法并辅以湍流模型求解流体相,采用DEM求解颗粒运动。非解析CFD-DEM模型的精度不如解析CFD-DEM模型,但计算效率更高,适用于管内颗粒两相流动问题。
管道根据布置方式可分为水平管、倾斜管和竖直管。早期实验研究和现阶段数值研究对象以水平和竖直管为主,倾斜管相对较少。学者已对水力输送的流动特性进行了广泛的实验研究[2, 7-11],并得到了众多经典的结论。但实验研究存在周期长、投入成本高和相关结论可能只在特定范围有效等缺点。基于连续介质法,Lahiri等[12]模拟了管内125和440 μm粒径玻璃珠的水浆流动,研究发现,颗粒在垂直面上分布不对称,不对称度随颗粒尺寸增加或流速降低而增加。Ofei等[13]指出水平管内颗粒-浆液摩擦压力损失随着颗粒粒径增加而减小。Messa等[14]在流体湍动能及其耗散率方程中引入特定源项,以解释湍流调制。
基于CFD-DEM方法,Uzi等[15]和Xiong等[16]分析了不同操作条件对水平管内粗颗粒两相流动特性,并对颗粒浓度分布和压降进行了定量分析。Zhou等[17]和张德胜等[18]研究了竖直管内不同操作参数对粗颗粒水力输送特性的影响。Zhao等[19]对各相间机制进行系统性地分析,并指出在颗粒体积分数大于3%时需考虑颗粒-湍流相互作用。李文馨[20]指出详细描述湍流-颗粒间相互作用对于实现复杂的移动床模拟是必不可少的。
本文建立了全耦合CFD-DEM颗粒水力输送模型,考虑了颗粒-流体相互作用和颗粒-湍流相互作用。基于扩散平均算法求解颗粒体积分数场;在k-ε湍流模型中添加特定源项以考虑颗粒对湍流的调制作用;同时添加离散随机游走模型以考虑湍流脉动对颗粒运动的随机影响。基于该模型研究了管道倾角对2 mm粒径颗粒水力输送特性的影响,并给出了降低固-液两相流输送系统内压降和能耗的建议。
1 数学模型 1.1 流体控制方程体积平均和Reynolds平均后的流体相连续方程和动量方程分别为:
| $ \frac{\partial}{\partial t}\left(\alpha_{\mathrm{f}} \rho_{\mathrm{f}}\right)+\nabla \cdot\left(\alpha_{\mathrm{f}} \rho_{\mathrm{f}} \bar{v}_{\mathrm{f}}\right)=0, $ | (1) |
| $ \begin{gathered} \frac{\partial}{\partial t}\left(\alpha_{\mathrm{f}} \rho_{\mathrm{f}} \bar{v}_{\mathrm{f}}\right)+\nabla \cdot\left(\alpha_{\mathrm{f}} \rho_{\mathrm{f}} \bar{v}_{\mathrm{f}} \bar{v}_{\mathrm{f}}\right)= \\ -\alpha_{\mathrm{f}} \nabla p+\nabla \cdot\left[\alpha_{\mathrm{f}}\left(\mu_{\mathrm{f}}+\mu_{\mathrm{t}}\right)\left(\nabla \bar{v}_{\mathrm{f}}+\nabla \bar{v}_{\mathrm{f}}^{\mathrm{T}}\right)\right] \\ +\alpha_{\mathrm{f}} \rho_{\mathrm{f}} g+f_{\mathrm{p}-\mathrm{f}} . \end{gathered} $ | (2) |
其中:αf、ρf、vf和p分别为流体体积分数、流体密度、流体平均速度和压力;t、g、μf和μt分别为时间、重力加速度、流体动力黏度和流体湍流黏度;fp-f为颗粒对流体的体积力源项。
湍流调制是颗粒对流体湍流的影响。相对于单相湍流,两相流中颗粒相的存在可以增强或减弱湍流。在标准k-ε湍流模型中添加湍动能源项Sk和湍流耗散源项Sε以考虑颗粒对湍流的影响[21]:
| $ S_k=\frac{1}{V_{\text {cell }}} \sum\limits_{i=1}^n 3 \pi \mu_{\mathrm{f}} d_i f_i\left|\boldsymbol{v}_{\mathrm{f}}-\boldsymbol{v}_i\right|^2, $ | (3) |
| $ S_{\varepsilon}=\rho_f C_{\varepsilon 3}^{\prime} \frac{\nu_{\mathrm{f}}^2}{V_{\mathrm{cell}}} \sum\limits_{i=1}^n f_i \frac{\left|\boldsymbol{v}_{\mathrm{f}}-\boldsymbol{v}_i\right|^2}{d_i} . $ | (4) |
其中:Sk和Sε分别为湍动能源项和湍流耗散源项;vf为流体瞬时速度;vi和di分别为颗粒i的速度和直径;fi和C′ ε3均为与颗粒Rep, i有关的系数,Rep, i=pfdi| vf- vi|/μf;Vcell和n分别为流体网格体积和流体网格内颗粒数;vf为流体运动黏度。
1.2 颗粒运动方程颗粒运动采用DEM求解,颗粒的运动由Newton第二定律描述:
| $ m_i \frac{\mathrm{~d} \boldsymbol{v}_i}{\mathrm{~d} t}=\boldsymbol{F}_{\mathrm{g}, i}+\boldsymbol{F}_{\mathrm{f}-\mathrm{p}, i}+\sum\limits_{j=1, j \neq i}^{k_{\mathrm{c}}} \boldsymbol{F}_{\mathrm{c}, i j}, $ | (5) |
| $ I_i \frac{\mathrm{~d} \omega_i}{\mathrm{~d} t}=\sum\limits_{j=1, j \neq i}^{k_{\mathrm{c}}}\left(\boldsymbol{T}_{\mathrm{c}, i j}+\boldsymbol{T}_{\mathrm{r}, i j}\right)+\boldsymbol{T}_{\mathrm{f}, i} . $ | (6) |
其中:mi、Fg, i、Ff-p, i和Fc, ij分别为颗粒i的质量、重力、流体对颗粒的总作用力和颗粒或壁面j对颗粒i的作用力,Ff-p, i= Fdrag, i+ Flift, i+ Fp, i+ Fvm, i,Fdrag, i、Flift, i、Fp, i和Fvm, i分别为曳力、升力、压力梯度力和虚拟质量力;kc为与颗粒i发生接触的颗粒数和壁面数的总和;Ii、ωi、Tc, ij、Tr, ij和Tf, i分别为颗粒i的转动惯量、角速度、颗粒切向力转矩、滚动摩擦转矩和流体作用转矩,Tc, ij= ri× Fct, ij,Tr, ij=-μs Fcn, ijri Ωi,Fct, ij和Fcn, ij分别为切向和法向接触力,ri、μs、ri和Ωi分别为颗粒质心到接触点的距离矢量、滚动摩擦因数、颗粒质心到接触点的距离、颗粒在接触点处单位角速度矢量。
1.3 流体-颗粒相间作用流体-颗粒间的耦合通过αf、流体-颗粒相互作用力项(Ff-p, i和fp-f)和湍流-颗粒相互作用项(Sk和Sε)实现。网格中颗粒体积分数的计算通过2个步骤实现。首先,将每个颗粒随机均匀地划分为Ntotal个特征点,每个特征点表征的体积为Vi/Ntotal,Vi为颗粒i的体积,根据每个网格内占据的特征点数计算颗粒体积分数的初始值:
| $ \alpha_{s, q}=\frac{\sum\limits_{i=1}^{k_q}\left(N_{i, q} V_i / N_{\text {total }}\right)}{V_{\text {cell }}} . $ | (7) |
其中:kq为有特征点位于网格q内的颗粒数;Ni, q为颗粒i在网格q内的特征点数;Ntotal本文中取48;αs, q为网格q内颗粒体积分数。由式(7)可得整个计算域内颗粒体积分数初始场α0(x)。
然后,使用基于扩散的平均方法[22-23]来确定计算域中的颗粒体积分数,用式(7)计算的初始场进行初始化,并在伪时间τ上求解αs(x, τ)瞬态扩散方程:
| $ \frac{\partial \alpha_{\mathrm{s}}}{\partial \tau}=\nabla^2 \alpha_{\mathrm{s}}, $ | (8a) |
| $ \alpha_{\mathrm{s}}(\boldsymbol{x}, \tau=0)=\alpha_0(\boldsymbol{x}) . $ | (8b) |
其中:
文[22-23]已经证明基于扩散的平均方法理论上等价于基于Gauss核的平均方法,并建立了两者等价的条件(带宽
fp-f的计算需排除压力梯度力[24],计算公式为
| $ \boldsymbol{f}_{\mathrm{p} - \mathrm{f}}=-\frac{1}{V_{\mathrm{cell}}} \sum\limits_{i=1}^n\left(\boldsymbol{F}_{\mathrm{drag}, i}+\boldsymbol{F}_{\mathrm{lift}, i}+\boldsymbol{F}_{\mathrm{vm}, i}\right) . $ | (9) |
曳力在两相作用力中占主导,因此对曳力的计算至关重要。Felice曳力模型[25]是常用的考虑孔隙率的曳力模型,Rong等[26]在Felice曳力模型的基础上进一步拓展了孔隙函数,使其适用于密集堆积颗粒流。本文依据文[26]计算Fdrag, i:
| $ \boldsymbol{F}_{\mathrm{drag}, i}=\frac{1}{8} \rho_{\mathrm{f}} C_{\mathrm{d}} \pi d_i^2\left|\boldsymbol{v}_{\mathrm{f}}-\boldsymbol{v}_i\right|\left(\boldsymbol{v}_{\mathrm{f}}-\boldsymbol{v}_i\right)\left(\alpha_{\mathrm{f}}^{2-\alpha}\right), $ | (10) |
| $ \begin{aligned} \alpha= & 2.65\left(\alpha_{\mathrm{f}}+1\right)-\left(5.3-3.5 \alpha_{\mathrm{f}}\right) \alpha_{\mathrm{f}}^2 \cdot \\ & \exp \left[-0.5\left(1.5-\log R e_{\mathrm{s}, i}\right)^2\right] . \end{aligned} $ | (11) |
其中:Cd为颗粒曳力系数;αf2-α为孔隙函数;Res, i为颗粒Reynolds数,Res, i=ρfdiαf| vf- vi|/μf,考虑了流体体积分数。
采用Loth和Dorgan模型[27]计算颗粒升力,在升力系数中综合考虑了流体剪切和颗粒旋转引起的升力作用:
| $ \boldsymbol{F}_{\text {lift }, i}=\frac{1}{8} \rho_{\mathrm{f}} C_l \pi d_i^2\left|v_{\mathrm{f}}-v_i\right|\left[\left(\boldsymbol{v}_{\mathrm{f}}-\boldsymbol{v}_i\right) \times \frac{\boldsymbol{\omega}_i}{\left|\boldsymbol{\omega}_i\right|}\right], $ | (12) |
| $ C_l=J^* \frac{12.92}{\pi} \sqrt{\frac{\omega_{\mathrm{f}}^*}{R e_{\mathrm{p}, i}}}+\omega_{\mathrm{eq}, i}^* C_1^* . $ | (13) |
其中:C1、J*和C1*分别为颗粒升力系数、近似函数和颗粒旋转系数;ωf*和ωeq, i*分别为相对流体涡度和相对颗粒角速度。相关量的计算公式参考文[27]。
在流固密度比大于0.1时,需要考虑虚拟质量力和压力梯度力,计算公式如下:
| $ \boldsymbol{F}_{\mathrm{p}, i}=-V_i \nabla p, $ | (14) |
| $ \boldsymbol{F}_{\mathrm{vm}, i}=C_{\mathrm{vm}} m_i \frac{\rho_{\mathrm{f}}}{\rho_i} \frac{\mathrm{~d}}{\mathrm{~d} t}\left(\boldsymbol{v}_{\mathrm{f}}-\boldsymbol{v}_i\right) . $ | (15) |
其中:ρi和Cvm分别为颗粒i的密度和虚拟质量力因数(默认取0.5)。
流体引起的颗粒转矩Tf, i与流体涡度和颗粒旋转角速度密切相关,Tf, i计算公式如下[28]:
| $ \boldsymbol{T}_{\mathrm{f}, i}=\frac{\rho_{\mathrm{f}}}{2}\left(\frac{d_i}{2}\right)^5 C_{\mathrm{r}}\left|\boldsymbol{\omega}_{\mathrm{f}-\mathrm{p}}\right| \boldsymbol{\omega}_{\mathrm{f}-\mathrm{p}} ; $ | (16) |
| $ C_{\mathrm{r}}= \begin{cases}\frac{64 \pi}{R e_{\mathrm{r}}}, & R e_{\mathrm{r}} \leqslant 32 ; \\ \frac{12.9}{R e_r^{0.5}}+\frac{128.4}{R e_r}, & 32<R e_{\mathrm{r}}<1000 .\end{cases} $ | (17) |
其中:Cr、Rer和ωf-p分别为转矩系数、颗粒旋转Reynolds数和流体-颗粒相对角速度。流体-颗粒相对角速度中考虑了流体涡度,
离散随机游走(discrete random walk, DRW)模型[29]用于计算湍流对颗粒运动的随机影响。流体瞬时速度vf由平均速度vf和脉动速度v ′ f组成。
| $ \boldsymbol{v}_{\mathrm{f}}=\overline{\boldsymbol{v}}_{\mathrm{f}}+\boldsymbol{v}_{\mathrm{f}}^{\prime}, $ | (18) |
| $ u^{\prime}=\xi \sqrt{\overline{\left(u^{\prime}\right)^2}}, \quad v^{\prime}=\xi \sqrt{\overline{\left(v^{\prime}\right)^2}}, \quad w^{\prime}=\xi \sqrt{\overline{\left(w^{\prime}\right)^2}} . $ | (19) |
其中:ξ为随机数;u′、v′和w′分别为v ′ f在x、y、z方向上的分量,且服从Gauss分布。
基于RANS模型的各向同性假设,均方根(root mean square, RMS)脉动速度的计算公式为
| $ \sqrt{\overline{\left(u^{\prime}\right)^2}}=\sqrt{\overline{\left(v^{\prime}\right)^2}}=\sqrt{\overline{\left(w^{\prime}\right)^2}}=\sqrt{\frac{2}{3} k_{\mathrm{f}}} . $ | (20) |
其中:kf为流体湍动能,通过k-ε湍流模型计算。理论上,各向同性假设在壁面附近不成立,该假设可能会导致流体轴向速度脉动削弱和其他方向速度脉动增加,这可能会影响颗粒的随机运动。但在水平和倾斜管中,重力、颗粒-颗粒和颗粒-壁面间作用占据主导,而湍流脉动对颗粒运动的随机影响较小[15]。在90°竖直管中,颗粒向管道中心运动,管道壁面附近颗粒很少。因此,壁面附近各向同性假设带来的误差是较小的。
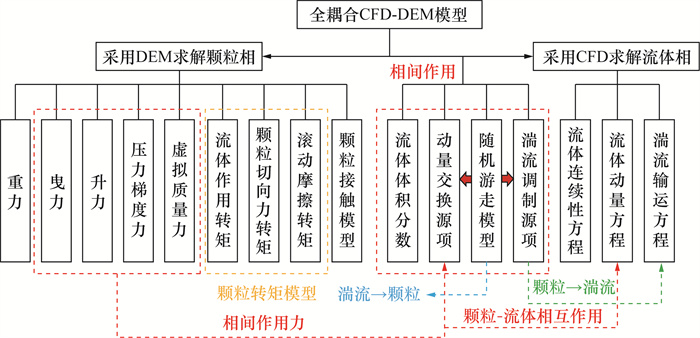
2 模型设置 2.1 数值格式图 1为全耦合CFD-DEM模型示意图。耦合模型实现了Euler场数据和Lagrange场数据间的传递和转换,并对颗粒体积分数、相间作用力和各源项进行计算。基于特征点法计算初始颗粒体积分数场,以该初始场求解瞬态扩散方程得到最终的颗粒体积分数场。除了曳力之外,升力、压力梯度力和虚拟质量力都在颗粒运动中定义。作用在颗粒上的总流体力以源项的形式添加到流体相动量方程中。此外,该模型还拓展了颗粒与湍流间相互作用机制,在RANS方法中考虑了湍流脉动速度对颗粒运动的随机影响,同时在湍流输运方程中添加湍动能源项和湍流耗散源项以考虑颗粒对湍流的调制机制。
|
| 图 1 全耦合CFD-DEM模型示意图 |
基于有限体积法求解流体方程,使用SIMPLE算法耦合速度-压力,对流项离散中采用二阶迎风格式。对颗粒运动方程进行显式积分,求解离散颗粒的平移和旋转,然后更新颗粒的位置和速度,以进行下一步耦合计算。考虑计算精度和时间成本,求解颗粒和流体相应物理量的时间步长分别为2×10-5和2×10-4 s。
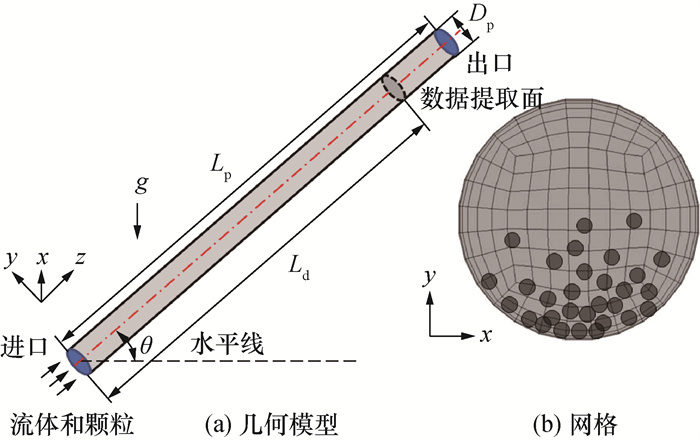
2.2 计算参数及边界条件本文采用文[2]实验模型,如图 2所示。2.0 mm粒径颗粒显示在网格中以说明颗粒尺寸与网格尺寸的相对大小关系。壁面第一层网格厚度为0.3 mm,且无量纲壁距y+为30~50。流体的进口设置为均匀速度,出口设置为自由出流;采用标准壁面函数处理固壁。颗粒以与流体相同的速度从进口射入,每秒射入的颗粒数由进口颗粒体积分数和流体速度确定。当颗粒从出口流出时,直接从模拟中去除。基于Hertz-Mindlin模型[17, 30-31]计算Fc, ij,采用一组弹簧-阻尼器来刻画颗粒在接触过程中的弹性变形和能量耗散,根据Coulomb摩擦定律,切向接触力存在最大值。
|
| 图 2 实验模型 |
表 1为参考文[17]使用的模拟参数。管道长度Lp和直径Dp分别为2.4 m和3.06 cm。在z为2.2 m处提取相应物理量,压降取自z为1.7和2.2 m处截面。模拟时间为4 s,从第2 s开始统计数据(对充分发展的流动进行足够时间的统计分析)。文[2]中实验采用90°竖直管,实验工况为:颗粒平均体积分数、流体平均速度和颗粒粒径分别为2.23%、1.89 m/s和2.32 mm。模型验证的管道和工况参数与实验相同。本文研究了管道倾角从0°到90°对粗颗粒水力输送特性的影响,进口颗粒体积分数cv、输送速度Uf和颗粒粒径dp分别为2.5%、3.0 m/s和2.0 mm。颗粒弛豫时间约为0.54 s,该值略小于颗粒从进口到出口所需时间。若颗粒从零流速启动,计算域长度需要大幅增加从而导致计算成本极大提高。本文中颗粒以与流体相同的速度从进口射入,有效减少了颗粒对流体运动的响应,避免颗粒弛豫时间过长导致计算域长度的大幅增加。从结果看,不同截面处(z为2 100、2 200和2 300 mm)颗粒体积分数、流体轴向速度和颗粒轴向速度的分布几乎完全重合,不随轴向距离变化。因此,模拟工况在所研究区域内已充分发展。
| 参数 | 数值 | 参数 | 数值 | |
| 颗粒密度/(kg·m-3) | 2 450 | 流体密度/(kg·m-3) | 998.2 | |
| 颗粒Poisson比 | 0.3 | 流体温度/℃ | 25 | |
| 颗粒Young模量/Pa | 1×107 | 流体动力黏度/(Pa·s) | 0.001 | |
| 颗粒-颗粒恢复因数 | 0.85 | 颗粒-壁面恢复因数 | 0.85 | |
| 颗粒-颗粒静摩擦因数 | 0.1 | 颗粒-壁面静摩擦因数 | 0.2 | |
| 颗粒-颗粒滚动摩擦因数 | 0.01 | 颗粒-壁面滚动摩擦因数 | 0.01 |
3 结果与讨论 3.1 模型验证
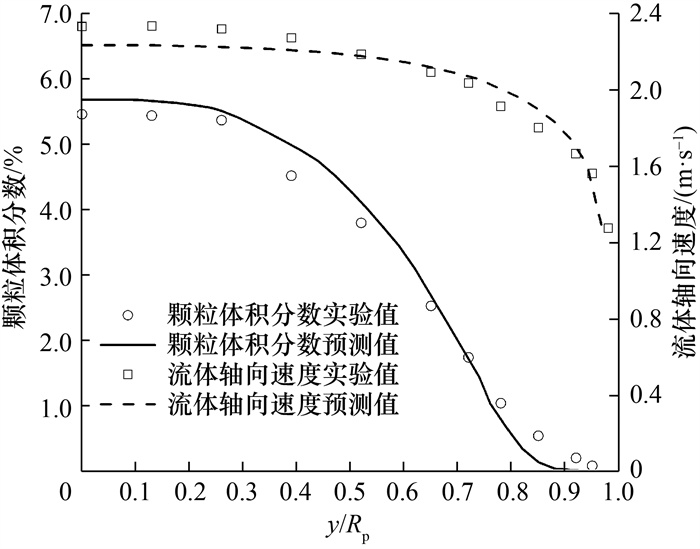
图 3为90°竖直管颗粒体积分数和流体轴向(z向)速度沿管径方向(y/Rp为无量纲径向位置,其中Rp为管道半径)计算结果,能很好地符合文[2]实验值。不同网格数(6万、9万和12万)和不同模拟时间(4、5和6 s)结果误差均小于7%。考虑计算精度和时间成本,采用中等网格和模拟时间为4 s的方案。
|
| 图 3 模型验证 |
3.2 倾角对颗粒的影响
图 4为倾角θ=0°~90°下沿y-z平面的颗粒分布及其轴向速度。在倾角θ=0°时,由于重力作用,颗粒沉积在管道底部形成较为密集的沉积床,床层底部颗粒以较低的速度向前运动,随着y增加,颗粒轴向速度逐渐增加。床层底部和中部颗粒主要以长期接触和滚动的形式向前运动,而部分颗粒在床层顶部以跳跃的形式向前运动。随着θ增加,颗粒间的间隙逐渐增大,且有逐渐向管道中心移动的趋势,沉积床的高度逐渐增加。在θ= 90°时,不再形成沉积床,颗粒在管道中心聚集以较高的速度运动,在管壁附近以较低的速度运动,呈现出与流体轴向速度相同的抛物线分布;相较于其他角度的管道,颗粒间隙最大。鉴于75°和90°工况差别较大,此处特别增加了82.5°和88°工况的结果,以展示其向对称分布发展的过程。82.5°工况下管道底部颗粒数量进一步降低,且颗粒间隙逐渐增大。θ为88°时,颗粒分布已非常接近90°管,但仍存在微弱偏心分布。

|
| 图 4 不同θ下颗粒分布及其轴向速度 |
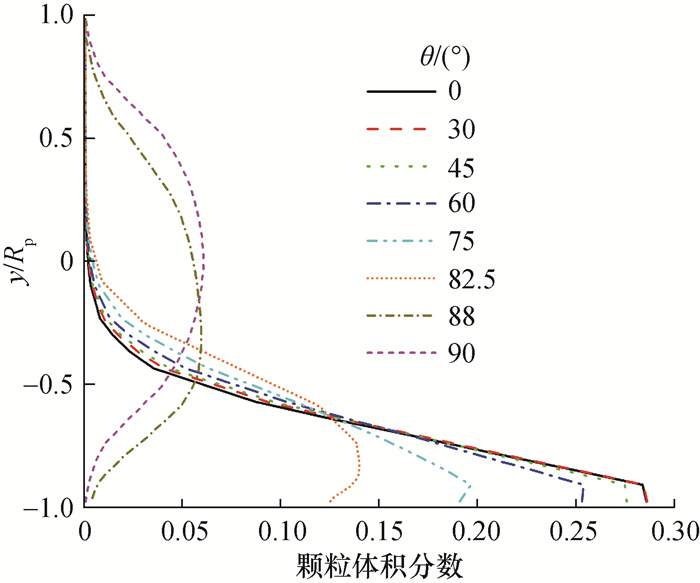
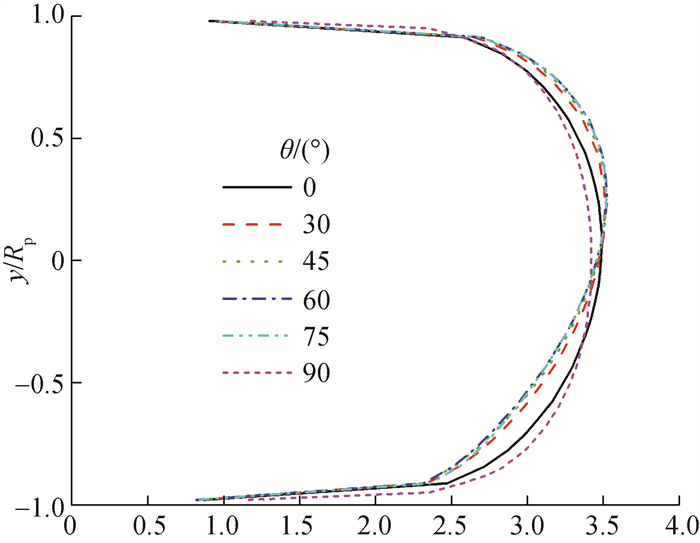
颗粒体积分数分布随θ变化如图 5所示。可以看出,在水平管和30°倾斜管道底部,颗粒体积分数最大,随着y方向高度的增加,颗粒体积分数逐渐降低。随着θ增加,管道底部颗粒体积分数逐渐降低,颗粒体积分数的分布逐渐向管道上部扩散。82.5°和88°工况很好地展现了管道底部颗粒体积分数逐渐降低以及颗粒体积分数逐渐向管道上部移动的趋势。在90°竖直管中,颗粒体积分数已达到近乎对称分布,颗粒在管道中心聚集,壁面处颗粒体积分数最少,这也符合实验观测[2]和数值模拟结果[17, 19]。
|
| 图 5 不同θ下颗粒体积分数 |
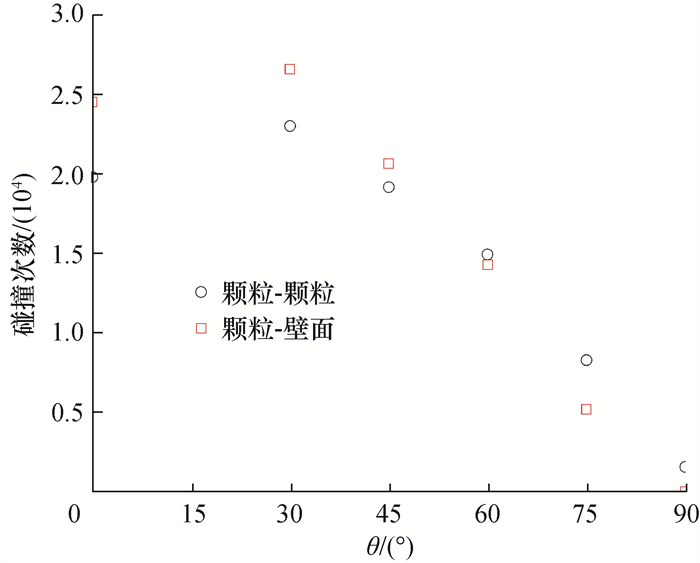
颗粒-颗粒和颗粒-壁面间碰撞次数随θ变化如图 6所示。随着θ增加,碰撞次数均先缓慢增加到最大值,后迅速减少,在θ=30°时最大。这是因为在θ=0°时颗粒重力不做功,管道底部颗粒能以较高的速度向前运动,而在30°管道中部分重力分量做负功,导致管道底部颗粒的速度存在一定量的下降,进而导致30°管道底部颗粒的间隙相对小于0°管道(如图 4所示)。这就导致小角度倾斜管内颗粒-颗粒和颗粒-壁面间碰撞次数存在少量增加。随着θ增加,重力和流动方向(z正方向)夹角从90°变为180°,即重力对颗粒径向分布的影响逐渐变小,而升力的影响相对变大。颗粒逐渐分散且远离墙壁,这导致颗粒-颗粒/壁面间碰撞次数均大大降低。不同之处在于,颗粒-壁面间碰撞次数在90°时减少至0,而颗粒-颗粒间碰撞次数在90°时未减少至0。因为在θ为90°时,由于升力作用,颗粒向管道中心聚集[17, 19],管道壁面处几乎没有颗粒,这导致管道中心仍存在颗粒-颗粒间碰撞,而颗粒-壁面间碰撞次数几乎为零。
|
| 图 6 不同θ下碰撞次数 |
3.3 倾角对流体的影响
不同θ下流体轴向速度分布如图 7所示。在θ= 0°时,流体轴向速度呈现出较好的对称分布。这是因为沉积床底部颗粒以较高速度运动,其对流体速度的影响较小。随着θ增加,由于颗粒运动滞后于流体,流体轴向速度逐渐向远离颗粒的区域(y正方向)偏离,即y正方向流体轴向速度逐渐增加,y负方向流体轴向速度逐渐降低,且在θ=60°时不对称程度达到最大。当继续增加θ时,流体轴向速度的偏心程度逐渐减小,在θ=90°时几乎不偏心。但由于需要克服颗粒重力做功,90°管内需要消耗更多的能量,这导致90°管道中心处流体轴向速度略小于水平管。
|
| 图 7 不同θ下流体轴向速度 |
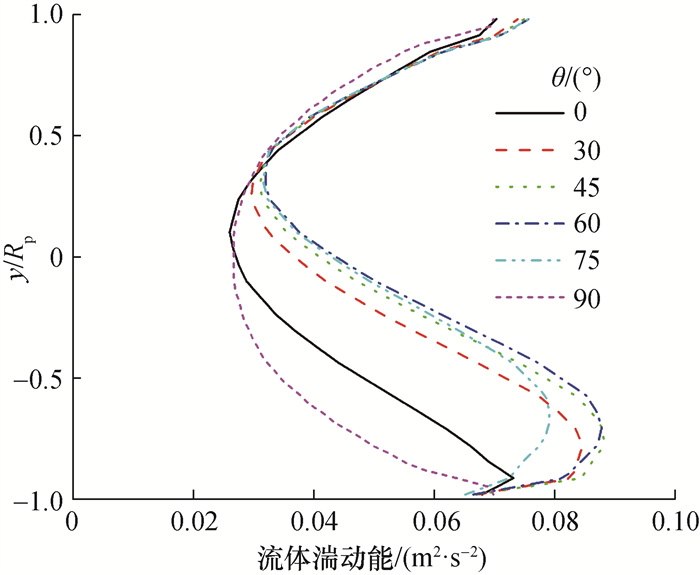
管内湍动能分布如图 8所示。θ为0°时,流体湍动能分布整体上未出现明显偏心,但管道底部湍动能略微不对称,这是因为颗粒集中在管道底部,颗粒产生的Sk和Sε对流体湍动能造成局部影响。随着θ增加,湍动能分布逐渐不对称,θ为60°时不对称程度达到最大,再继续增加倾角,流体湍动能分布的不对称程度逐渐减小,直到90°时湍动能分布再次对称。在水平和倾斜工况中,颗粒较为密集地堆积在管道底部,底部较高的颗粒体积分数对局部湍动能的影响较大;而管道顶部较低的颗粒体积分数对局部湍动能的影响很小。在竖直工况中,颗粒在整个截面范围内更分散(除管道中心区域0.5 < y/Rp < 0.5,其他区域内颗粒体积分数均低于3%,见图 5),根据Zhao等[19]的研究,颗粒体积分数 < 3% 时颗粒对局部湍动能的影响很小。因此,竖直工况中颗粒对流体湍动能的影响较其他角度工况更小。本文研究重点为管道主流区域流体湍动能的变化情况,而不关注壁面附近湍动能的变化,因此未给出壁面附近流体湍动能的详细变化情况。
|
| 图 8 不同θ下流体湍动能 |
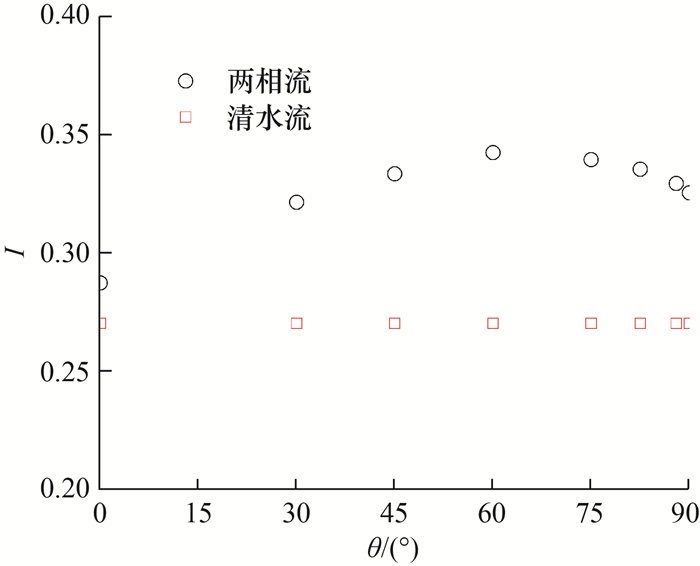
压降与颗粒水力输送系统的能耗密切相关,是实际工程应用中备受关注的问题之一。无量纲压降I被广泛应用于颗粒水力输送系统,I=Δp/(ΔLρfg),其中ΔL和Δp分别为研究区域内两截面间的距离和两截面上压力差。图 9对比了相同体积流量下无颗粒负载的清水流和进口颗粒体积分数为2.5%的两相流中I随θ的变化情况。需要注意的是,I的计算中排除了重力引起的流体静压变化。根据式(2),在清水流中I主要由流体粘性应力引起,其不随倾角变化;在固-液两相流中I主要由流体粘性应力和颗粒共同影响,其随着θ增加先逐渐增加后减小,在θ为60°时压降最大。两相流压降始终大于清水流压降,这是因为颗粒的存在造成更多的能量损耗。
|
| 图 9 θ对无量纲压降影响 |
两相流内压降与总能量耗散密切相关,总能耗由流体能耗和颗粒能耗组成。流体能耗包括流体平均速度、脉动速度和流体-壁面间剪切引起的能耗,颗粒能耗包括克服颗粒重力做功、颗粒-流体相对运动、颗粒-颗粒和颗粒-壁面间碰撞摩擦引起的能耗。在充分发展的水平管内,颗粒重力几乎不对颗粒做功,颗粒-颗粒/壁面间碰撞摩擦能耗较大。当θ从0°增加到60°时颗粒重力引起的能耗迅速增加,当θ继续增加到90°时该能耗缓慢增加;同时颗粒-颗粒和颗粒-壁面间碰撞摩擦能耗会逐渐减小。Zhang等[32]的研究指出,流体脉动速度和颗粒重力引起的能耗是影响倾斜管内压降和总能耗变化的最主要因素;θ为0°~60°时压降和总能耗增加的主要原因是流体脉动速度和颗粒重力引起的能耗均增加;而θ为60°~90°时压降和总能耗减小的主要原因是流体脉动速度引起的能耗减小量大于颗粒重力能耗的增加量。因此,为降低输送系统能耗,在实际工程应用中,应避免使用60°倾斜管输送颗粒,在需要进行颗粒提升时使用90°管道,在无需进行颗粒提升时使用水平管或小角度倾斜管。
4 结论本文建立了全耦合CFD-DEM颗粒水力输送模型,综合考虑了相间作用力和颗粒-湍流间相互作用,更适合于密集颗粒流。经验证,模型能够准确预测管内颗粒空间分布和两相速度特性。基于该模型进一步分析了管道倾角对粗颗粒管内水力输送特性的影响,主要结论如下:
1) 当θ为0°时,颗粒沉降在管道底部形成沉积床,床层顶部颗粒以较高速度向前运动,而中部和底部颗粒以较低速度向前运动。流体轴向速度分布近乎对称,而流体湍动能在底部略微不对称。
2) 随着θ增加,颗粒分布逐渐松散,且逐渐向管道中心聚集。颗粒-颗粒和颗粒-壁面间碰撞次数均先略微增加后迅速减少。随着θ增加,流体轴向速度和湍动能分布均先逐渐不对称后恢复对称,在θ为60°时不对称程度最大。
3) 相同体积流量下,两相流压降始终比清水流压降大,清水流压降几乎不随θ变化,而两相流压降随θ增加先增加后减小,在θ为60°时达到最大。在工程应用中,输送颗粒应避免使用60°倾斜管,尽可能使用小角度或大角度倾斜管。
| [1] |
ABULNAGA B E. Slurry systems handbook[M]. New York: McGraw-Hill, 2002.
|
| [2] |
ALAJBEGOVIC' A, ASSAD A, BONETTO F, et al. Phase distribution and turbulence structure for solid/fluid upflow in a pipe[J]. International Journal of Multiphase Flow, 1994, 20(3): 453-479. DOI:10.1016/0301-9322(94)90021-3 |
| [3] |
LI Y, ZHANG H B, LIN Z, et al. Relationship between wear formation and large-particle motion in a pipe bend[J]. Royal Society Open Science, 2019, 6(1): 181254. DOI:10.1098/rsos.181254 |
| [4] |
UZI A, BEN AMI Y, LEVY A. Erosion prediction of industrial conveying pipelines[J]. Powder Technology, 2017, 309: 49-60. DOI:10.1016/j.powtec.2016.12.087 |
| [5] |
VAEZI M, KUMAR A. Pipeline hydraulic transport of biomass materials: A review of experimental programs, empirical correlations, and economic assessments[J]. Biomass and Bioenergy, 2015, 81: 70-82. DOI:10.1016/j.biombioe.2015.06.001 |
| [6] |
XU L, ZHANG Q, ZHENG J Y, et al. Numerical prediction of erosion in elbow based on CFD-DEM simulation[J]. Powder Technology, 2016, 302: 236-246. DOI:10.1016/j.powtec.2016.08.050 |
| [7] |
MATOUSEK V. Pressure drops and flow patterns in sand-mixture pipes[J]. Experimental Thermal and Fluid Science, 2002, 26(6-7): 693-702. DOI:10.1016/S0894-1777(02)00176-0 |
| [8] |
李鹏程. 粗颗粒垂直管水力提升规律研究[D]. 北京: 清华大学, 2007. LI P C. Studies on mechanism of hydraulic hoist of coarse particle in vertical pipe [D]. Beijing: Tsinghua University, 2007. (in Chinese) |
| [9] |
SAD CHEMLOUL N, BENRABAH O. Measurement of velocities in two-phase flow by laser velocimetry: Interaction between solid particles' motion and turbulence[J]. Journal of Fluids Engineering, 2008, 130(7): 071301. DOI:10.1115/1.2948358 |
| [10] |
RAVELET F, BAKIR F, KHELLADI S, et al. Experimental study of hydraulic transport of large particles in horizontal pipes[J]. Experimental Thermal and Fluid Science, 2013, 45: 187-197. DOI:10.1016/j.expthermflusci.2012.11.003 |
| [11] |
VLASÁK P, CHÁRA Z, KRUPIČKA J, et al. Experimental investigation of coarse particles-water mixture flow in horizontal and inclined pipes[J]. Journal of Hydrology and Hydromechanics, 2014, 62(3): 241-247. DOI:10.2478/johh-2014-0022 |
| [12] |
LAHIRI S K, GHANTA K C. Slurry flow modelling by CFD[J]. Chemical Industry and Chemical Engineering Quarterly, 2010, 16(4): 295-308. DOI:10.2298/CICEQ091030031L |
| [13] |
OFEI T N, ISMAIL A Y. Eulerian-Eulerian simulation of particle-liquid slurry flow in horizontal pipe[J]. Journal of Petroleum Engineering, 2016, 2016: 5743471. |
| [14] |
MESSA G V, MALAVASI S. Numerical prediction of dispersed turbulent liquid-solid flows in vertical pipes[J]. Journal of Hydraulic Research, 2014, 52(5): 684-692. DOI:10.1080/00221686.2014.939110 |
| [15] |
UZI A, LEVY A. Flow characteristics of coarse particles in horizontal hydraulic conveying[J]. Powder Technology, 2018, 326: 302-321. DOI:10.1016/j.powtec.2017.11.067 |
| [16] |
XIONG T, ZHANG X Z, MIEDEMA S A, et al. Study of the characteristics of the flow regimes and dynamics of coarse particles in pipeline transportation[J]. Powder Technology, 2019, 347: 148-158. DOI:10.1016/j.powtec.2019.02.031 |
| [17] |
ZHOU M M, WANG S, KUANG S B, et al. CFD-DEM modelling of hydraulic conveying of solid particles in a vertical pipe[J]. Powder Technology, 2019, 354: 893-905. DOI:10.1016/j.powtec.2019.07.015 |
| [18] |
张德胜, 周游, 赵睿杰, 等. 垂直管内固-液两相流全耦合CFD-DEM模型研究[J]. 农业机械学报, 2022, 53(12): 212-222. ZHANG D S, ZHOU Y, ZHAO R J, et al. Solid-liquid two-phase flow based on fully coupled CFD-DEM method in vertical pipe[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53(12): 212-222. (in Chinese) |
| [19] |
ZHAO R J, ZHOU Y, ZHANG D S, et al. Numerical investigation of the hydraulic transport of coarse particles in a vertical pipe based on a fully-coupled numerical model[J]. International Journal of Multiphase Flow, 2022, 155: 104094. DOI:10.1016/j.ijmultiphaseflow.2022.104094 |
| [20] |
李文馨. 基于DEM的欧拉-拉格朗日水沙两相流数学模型及其应用[D]. 北京: 清华大学, 2023. LI W X. Development and application of a DEM-based Euler-Lagrange model for sediment transport [D]. Beijing: Tsinghua University, 2023. (in Chinese) |
| [21] |
CROWE C T, SCHWARZKOPF J D, SOMMERFELD M, et al. Multiphase flows with droplets and particles: 2nd ed[M]. Boca Raton: CRC Press, 2012.
|
| [22] |
SUN R, XIAO H. Diffusion-based coarse graining in hybrid continuum-discrete solvers: Theoretical formulation and a priori tests[J]. International Journal of Multiphase Flow, 2015, 77: 142-157. DOI:10.1016/j.ijmultiphaseflow.2015.08.014 |
| [23] |
SUN R, XIAO H. Diffusion-based coarse graining in hybrid continuum-discrete solvers: Applications in CFD-DEM[J]. International Journal of Multiphase Flow, 2015, 72: 233-247. DOI:10.1016/j.ijmultiphaseflow.2015.02.014 |
| [24] |
ZHOU Z Y, KUANG S B, CHU K W, et al. Discrete particle simulation of particle-fluid flow: Model formulations and their applicability[J]. Journal of Fluid Mechanics, 2010, 661: 482-510. DOI:10.1017/S002211201000306X |
| [25] |
DI FELICE R. The voidage function for fluid-particle interaction systems[J]. International Journal of Multiphase Flow, 1994, 20(1): 153-159. DOI:10.1016/0301-9322(94)90011-6 |
| [26] |
RONG L W, DONG K J, YU A B. Lattice-Boltzmann simulation of fluid flow through packed beds of uniform spheres: Effect of porosity[J]. Chemical Engineering Science, 2013, 99: 44-58. DOI:10.1016/j.ces.2013.05.036 |
| [27] |
LOTH E, DORGAN A J. An equation of motion for particles of finite Reynolds number and size[J]. Environmental Fluid Mechanics, 2009, 9(2): 187-206. DOI:10.1007/s10652-009-9123-x |
| [28] |
RUBINOW S I, KELLER J B. The transverse force on a spinning sphere moving in a viscous fluid[J]. Journal of Fluid Mechanics, 1961, 11(3): 447-459. DOI:10.1017/S0022112061000640 |
| [29] |
GOSMAN A D, LOANNIDES E. Aspects of computer simulation of liquid-fueled combustors[J]. Journal of Energy, 1983, 7(6): 482-490. DOI:10.2514/3.62687 |
| [30] |
HERTZ H. On the contact of elastic solids[J]. Journal für die Reine und Angewandte Mathematik, 1882, 92: 156-171. |
| [31] |
MINDLIN R D, DERESIEWICZ H. Elastic spheres in contact under varying oblique forces[J]. Journal of Applied Mechanics, 1953, 20(3): 327-344. DOI:10.1115/1.4010702 |
| [32] |
ZHANG L, ZHOU Y, SI Q R, et al. Coarse particle-laden flows and energy dissipation in inclined hydraulic conveying pipes[J]. Particulate Science and Technology, 2023, 1-19. |



