放射性物质可能通过大气沉降、地表水和地下水途径进入某区域的土壤,造成放射性污染。随着自然风或人为活动引起的物理扰动,土壤中颗粒可能从地面再悬浮至空气中[1]。一些难以通过食物链向人体内转移的核素(如铀等),却很可能以再悬浮颗粒的形式被人体吸入造成内照射,所以探究放射性气溶胶颗粒的再悬浮行为,对悬浮颗粒的控制意义重大。已有研究者围绕气溶胶颗粒的再悬浮开展了再悬浮因子估算方法的研究,如Healy等[2]和Oztunali等[3]对用于估算土壤中放射性气溶胶颗粒再悬浮的释放模式(再悬浮因子模式、再悬浮率估算模式)进行了分析,发现这2种模式都需要根据经验数据来确定再悬浮因子的值和可能产生的再悬浮土壤厚度。Cleaver等[4]、杜嘉陵[5]和Zhang[6]基于土壤表面颗粒物的受力情况建立了颗粒物的能量、动量、质量守恒方程组,并采用数值求解方式模拟计算土壤表面颗粒物的再悬浮释放量。
近年来,在某些核电站严重事故工况中,放射性气溶胶颗粒会沉降于安全壳壁面,并因水池持续沸腾以及氢气爆炸等引入的扰动气流等以再悬浮形式重新释放,导致安全壳内放射性气溶胶颗粒浓度的再次上升。已有研究常采用计算流体力学(computational fluid dynamics,CFD)开展沉降于壁表面的气溶胶再悬浮的数值模拟研究[7-10],如黄挺等[9]以用于RnR模型验证的气溶胶再悬浮试验的设计参数及条件为基础,利用GASFLOW程序构建分析模型进行模拟计算,结果表明在发生再悬浮的主要阶段,GASFLOW程序能较好地模拟气溶胶再悬浮行为;在较低气流速度的条件下,RnR模型分析结果更接近试验数据;在较高气流速度的条件下,GASFLOW程序分析得出的结果更加保守。江斌等[10]利用GASFLOW程序分析了气溶胶的再悬浮行为,结果表明,GASFLOW程序能较好地模拟气溶胶的再悬浮行为,清晰直观地展示不同时刻气溶胶的位置分布。
使用CFD软件求解流体流动和传热问题,是依据空气流动的数学物理模型,将空间分成小的控制体,把空气流动连续的微分控制方程组离散为非连续的代数组,结合实际的边界条件,并用计算机数值解析求解。它提供的非结构网格生成程序,对相对复杂的几何结构网格生成非常有效。此外,还可根据计算结果调整网格,这种网格的自适应能力对于精确求解含较大梯度的流场具有实际意义。以上特点使得CFD软件在模拟气溶胶运动扩散问题中极具优势。然而,现有CFD研究多针对放射性气溶胶颗粒在管壁的再悬浮问题开展,关于污染土壤中放射性气溶胶颗粒再悬浮释放的CFD研究较少。
因此,本文使用CFD软件模拟进风引起的放射性气溶胶颗粒的再悬浮运动过程和运动轨迹。研究结果可为放射性气溶胶颗粒的沉降和再悬浮实验设计提供依据,也可为放射性污染区域工作或者活动人员的辐射防护行动提供指导。
1 数值模型的建立本文使用CFD软件,对进风引起的放射性气溶胶颗粒的再悬浮运动过程开展模拟,研究再悬浮箱体内气流场分布特征和再悬浮气溶胶颗粒的运动扩散规律。数值模型设计如下所述。
1.1 流体流动控制方程1) 质量守恒方程。
| $ \frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}+\frac{\partial(\rho v)}{\partial y}+\frac{\partial(\rho w)}{\partial z}=0 . $ | (1) |
其中:ρ为流体密度;t为时间;u, v, w为流体速度矢量在x, y, z方向上的分量。
2) 动量守恒方程。
| $ \begin{gathered} \frac{\partial(\rho u)}{\partial t}+\operatorname{div}(\rho u \boldsymbol{U})= \\ \operatorname{div}(\eta \cdot \operatorname{grad}(u))-\frac{\partial p}{\partial x}+s_u, \end{gathered} $ | (2) |
| $ \begin{gathered} \frac{\partial(\rho v)}{\partial t}+\operatorname{div}(\rho v \boldsymbol{U})= \\ \operatorname{div}(\eta \cdot \operatorname{grad}(v))-\frac{\partial p}{\partial y}+s_v, \end{gathered} $ | (3) |
| $ \begin{gathered} \frac{\partial(\rho w)}{\partial t}+\operatorname{div}(\rho w \boldsymbol{U})= \\ \operatorname{div}(\eta \cdot \operatorname{grad}(w))-\frac{\partial p}{\partial z}+s_w. \end{gathered} $ | (4) |
其中:U为流体速度矢量;η为流体的动力黏度;p为压力;su、sv、sw为动量方程的广义源项;div()表示散度;grad()表示梯度。
3) 能量守恒方程。
| $ \frac{\partial T}{\partial t}+\operatorname{div}(\boldsymbol{U} T)=\operatorname{div}\left(\frac{\lambda}{\rho c_p} \cdot \operatorname{grad}(T)\right)+\frac{S_{\mathrm{h}}+\varPhi}{\rho} . $ | (5) |
其中:T为温度,λ、cp分别为流体的导热系数和比热,Sh、Φ分别为流体的内热源和耗散函数。
1.2 湍流方程采用标准k-ε两方程模型,湍流脉动动能方程和脉动动能耗散率方程如式(6)和式(7)[11]所示。
| $ \begin{gathered} \rho \frac{\partial k}{\partial t}+\rho u_j \frac{\partial k}{\partial x_j}= \\ \frac{\partial}{\partial x_j}\left[\left(\eta+\frac{\eta_{\mathrm{t}}}{\sigma_k}\right) \frac{\partial k}{\partial x_j}\right]+\eta_t \frac{\partial u_i}{\partial x_j}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\rho \varepsilon, \end{gathered} $ | (6) |
| $ \begin{gathered} \rho \frac{\partial \varepsilon}{\partial t}+\rho u_n \frac{\partial \varepsilon}{\partial x_n}=\frac{\partial}{\partial x_n}\left[\left(\eta+\frac{\eta_{\mathrm{t}}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_n}\right]+ \\ \frac{c_1 \varepsilon}{k} \eta_{\mathrm{t}} \frac{\partial u_i}{\partial x_j}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-c_2 \rho \frac{\varepsilon^2}{k} . \end{gathered} $ | (7) |
其中:k为湍流脉动动能;xi, xj, xn分别为x, y, z方向上节点的位置;ui, uj, un分别为xi, xj, xn处的速度;σk为脉动动能的Prandtl数,取值为1;ηt为湍流黏性系数,ηt= cμρk2/ε,其中cμ为经验系数,取值为0.09;ε为脉动动能耗散率;σε为经验常数,取值为1.3;c1和c2均为经验系数,取值分别为1.44和1.92。
1.3 离散相模型采用离散相(discrete phase model,DPM)模型[12, 13]进行气固两相流动的求解。以x方向为例,颗粒的力的平衡方程如下:
| $ \frac{\mathrm{d} u_{\mathrm{p}}}{\mathrm{~d} t}=F_{\mathrm{D}}\left(u_{\mathrm{a}}-u_{\mathrm{p}}\right)+g_x-\frac{\rho_{\mathrm{a}}}{\rho_{\mathrm{p}}} g_x+F_{\mathrm{x}} . $ | (8) |
其中:up、ua、ρp、ρa、FD、Fx分别为颗粒运动速度、空气速度、颗粒密度、空气密度、颗粒受到的流体曳力以及颗粒受到的其他外力;gx为单位质量重力在x方向上的分力。上式左侧表示颗粒的惯性力,右侧的第1项表示曳力,第2项表示重力以及浮升力,第3项表示其他外力。
2 边界条件设置将送风口设为速度入口,根据某市年平均风速10 m/s,将进风口风速设置为10 m/s;排风口设为出流边界;壁面设为固壁边界条件;设置地面为产生放射性气溶胶颗粒的面源(surface source),该面源将产生具有放射性的铀气溶胶颗粒,颗粒粒径为2.5 μm,颗粒密度为1.65 g/cm3。喷射源的喷射量为1×10-5 kg/s,喷射时间为0.5 s。
采用瞬态计算再悬浮气溶胶颗粒的运动扩散特性,以得到颗粒的状态与运动轨迹随时间和空间的变化。湍流模型采用标准k-ε两方程模型,选用压力和速度耦合的SIMPLE算法,标准压力,离散格式选用二阶迎风格式。
3 几何模型建立使用Solid Works软件对再悬浮箱体进行三维建模,如图 1所示。再悬浮箱体参考了法国核辐射保护及核安全研究所(Institute for Radiation Protection and Nuclear Safety,IRSN)的CEPIA试验平台所用的几何模型[14],空间尺寸为3.9 m× 2.9 m×2.9 m,模型箱体上端设置4个进风口,下端设置4个排风口,进风口和排风口尺寸均为0.3 m×0.1 m。在箱体底面产生具有放射性的铀气溶胶颗粒,进风口的通风引起箱体内气流扰动,导致气固交界面上放射性气溶胶颗粒因风力作用的再悬浮。
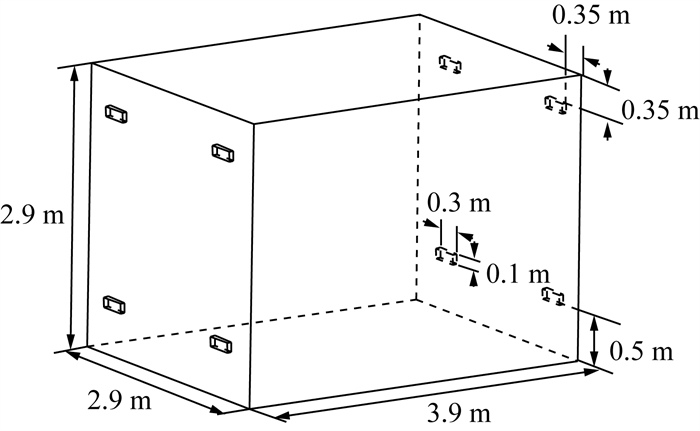
|
| 图 1 再悬浮箱体几何模型 |
使用ICEM CFD软件进行网格划分,结果如图 2所示,再悬浮箱体的几何结构简单,六面体网格质量比四面体更好,在收敛性能上也明显更优,故采用结构化六面体网格对进排风口分别进行局部加密处理,划分网格总数为342 056个。
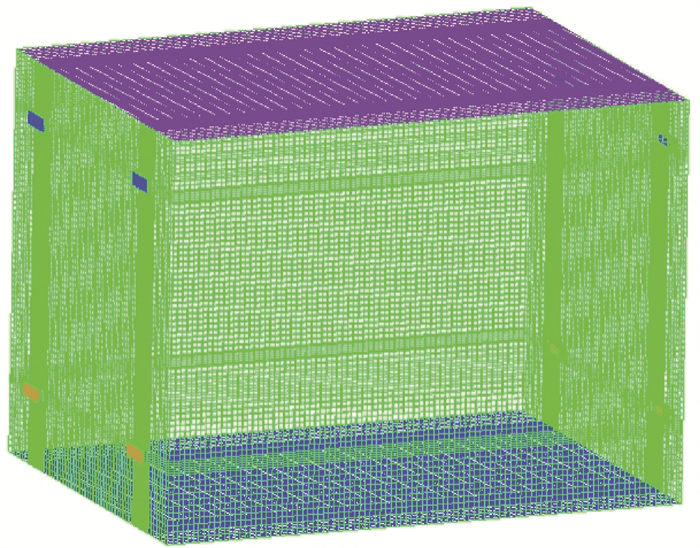
|
| 图 2 计算域网格 |
网格密度对于模拟计算的精确性有重要影响,为了保证计算结果可靠,同时降低网格划分的工作量以提高计算效率,对网格进行无关性验证,结果如表 1所示。由图可知,网格数量为342 056时已经符合网格无关性。
| 网格数/个 | 平面y=0.03 m上的平均速度/(m·s-1) |
| 88 900 | 0.154 |
| 168 903 | 0.197 |
| 258 960 | 0.256 |
| 342 056 | 0.329 |
| 445 085 | 0.331 |
4 数值模拟与结果分析
模拟得到的空间气流场分布结果如图 3所示。由图可知,整个再悬浮箱体内的气流场分布均匀,形成了较大的湍流,这表明这种进、排风口位置的布置方式具有一定的优势,能使箱体内形成较完整的涡流流动效果,整体速度分布也较均匀。
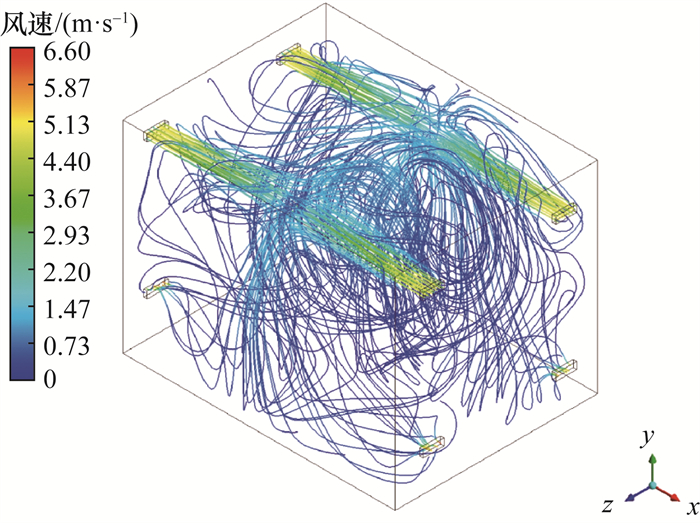
|
| 图 3 空间气流场分布 |
基于图 3所示的空间气流场分布,获得近地面速度分布云图如图 4所示,由图可知,近地面处风速较大,可将地面的颗粒载带起来。颗粒表面的风速约为0.01~0.21 m/s。该市年平均风速为10 m/s,按照风廓线系数推导得出地面0.02 m高处的风速为0.04~1.22 m/s,其中风扩散系数参照《核环境学基础》中表4.12中山区或城市区域D类稳定度下的取值[15],为0.4。这表明再悬浮箱体近地面处中心区域的模拟风速(0.01~0.21 m/s)处于该地区地表面风速(0.04~1.22 m/s)范围内,能很好地表征地表风速对放射性气溶胶颗粒再悬浮的影响。
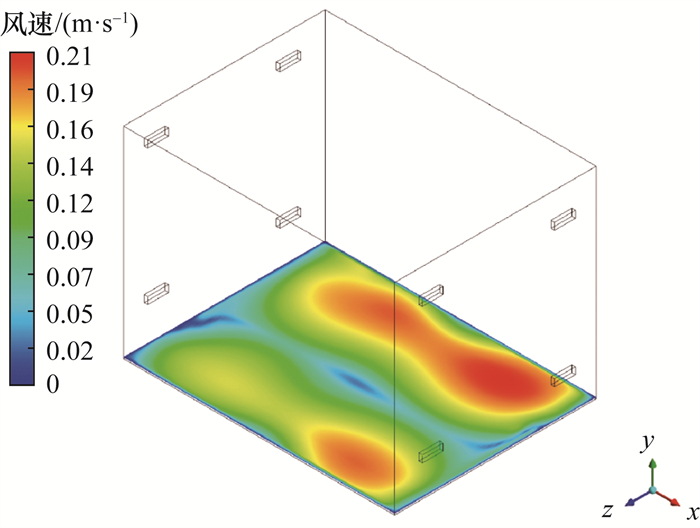
|
| 图 4 近地面速度分布云图(y=0.02 m) |
通过展现t=0.1、4、8、12、16、20 s时刻箱体内再悬浮气溶胶颗粒的运动分布状态,分析放射性气溶胶颗粒的再悬浮运动过程。如图 5所示,进风口的通风引起箱体内气流发生剧烈扰动,在箱体内形成了近似与平面x=0对称的气流场。0~4 s时,在空间内气流的带动下,地面上的气溶胶颗粒被风吹起并随气流逐渐向箱体侧壁面运动;4~8 s时,气溶胶颗粒到达侧壁面后,少部分颗粒会附着在壁面上,大部分颗粒转而继续向上运动;8~12 s时,靠近排风口的部分再悬浮颗粒会通过排风口直接排出,剩余的再悬浮颗粒被气流裹挟着继续向上运动;12~16 s时,再悬浮颗粒在箱体内环绕,经过进风口之后又向箱体中部运动;20 s时,气溶胶颗粒已经均匀地充斥在整个再悬浮箱体中。由此可见,进风口速度设置为10 m/s足以将地面的颗粒载带起来;20 s时箱体内气溶胶颗粒已经混合得十分充分,空间气流分布均匀。
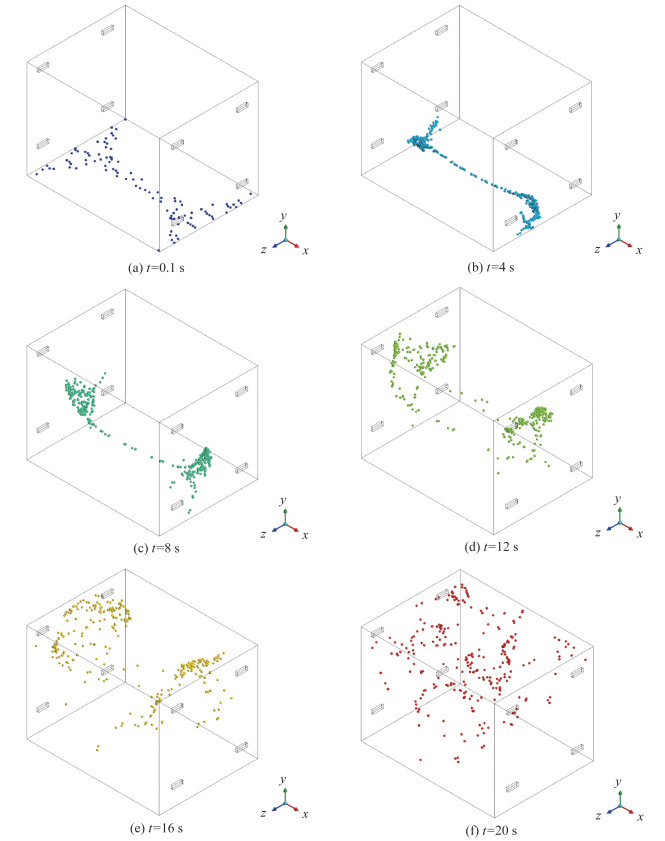
|
| 图 5 放射性气溶胶颗粒的再悬浮运动过程的分时模拟 |
从上述模拟结果可知,当进风口风速为10 m/s时,再悬浮箱体内气流发生剧烈扰动的同时,对地面的气溶胶颗粒载带作用较强,颗粒再悬浮量较多,便于气溶胶颗粒的采样和测量。
5 结论本文通过CFD仿真的方法,开展了污染场地放射性气溶胶颗粒再悬浮释放的模拟研究,得到了进风引起的放射性气溶胶颗粒的再悬浮运动过程,并分析了进排风口设置对气流场分布特征的影响。结果表明:
1) 进风口风速为10 m/s时,再悬浮箱体内气流分布均匀,涡流流动足以引起地面上放射性气溶胶颗粒的再悬浮,且颗粒再悬浮量较多,便于气溶胶采样和测量。
2) 再悬浮箱体近地面处中心区域的模拟风速大小处于该地区地表面风速范围内,能很好表征该地区地表风速对放射性气溶胶颗粒再悬浮的影响。
本次模拟计算可为后续进行自然环境和扰动环境下放射性气溶胶颗粒的沉降和再悬浮实验设计提供依据,并为在放射性污染区域工作或者活动人员的辐射防护行动提供指导。
| [1] |
陈海龙, 廉冰, 于志翔, 等. 137Cs沉降再悬浮因子/率估算方法研究[J]. 核电子学与探测技术, 2018, 38(4): 511-515. CHEN H L, LIAN B, YU Z X, et al. Research of 137Cs resuspension factor/rate estimated methods[J]. Nuclear Electronics & Detection Technology, 2018, 38(4): 511-515. DOI:10.3969/j.issn.0258-0934.2018.04.013 (in Chinese) |
| [2] |
HEALY J W, RODGERS J C. Limits for the burial of the department of energy transuranic wastes[R]. Los Alamos: Los Alamos National Lab, 1979.
|
| [3] |
OZTUNALI O I, RÉ G C, MOSKOWITZ P M, et al. Data base for radioactive waste management, impacts analyses methodology report[R]. White Plains: Dames and Moore, 1981.
|
| [4] |
CLEAVER J W, YATES B. Mechanism of detachment of colloidal particles from a flat substrate in a turbulent flow[J]. Journal of Colloid and Interface Science, 1973, 44(3): 464-474. DOI:10.1016/0021-9797(73)90323-8 |
| [5] |
杜嘉陵. 循环紊流中气载粒子的沉淀和再悬浮[J]. 原子能科学技术, 1996, 30(6): 502-508. DU J L. Deposition and resuspention of gas-borne particles in recirculating turbulent flows[J]. Atomic Energy Science and Technology, 1996, 30(6): 502-508. (in Chinese) |
| [6] |
ZHANG F. The modelling of particle resuspension in a turbulent boundary layer[D]. Newcastle: Newcastle University, 2011.
|
| [7] |
黄挺, 江斌, 陈炼. 基于STORM试验的GASFLOW气溶胶再悬浮模型评估与改进[J]. 原子能科学技术, 2021, 55(3): 474-480. HUANG T, JIANG B, CHEN L. Evaluation and improvement of aerosol resuspension model in GASFLOW based on STORM test[J]. Atomic Energy Science and Technology, 2021, 55(3): 474-480. (in Chinese) |
| [8] |
陈林林, 魏严凇, 史晓磊, 等. 安全壳内剥蚀引起的气溶胶颗粒再悬浮[J]. 中国粉体技术, 2020, 26(5): 1-6. CHEN L L, WEI Y S, SHI X L, et al. Aerosol resuspension behavior caused by denudation in containment[J]. China Powder Science and Technology, 2020, 26(5): 1-6. (in Chinese) |
| [9] |
黄挺, 江斌, 陈炼. GASFLOW中气溶胶再悬浮模型与RnR模型对比研究[J]. 原子能科学技术, 2020, 54(12): 2424-2430. HUANG T, JIANG B, CHEN L. Comparative study between aerosol resuspension model in GASFLOW and RnR Model[J]. Atomic Energy Science and Technology, 2020, 54(12): 2424-2430. DOI:10.7538/yzk.2019.youxian.0928 (in Chinese) |
| [10] |
江斌, 黄挺, 陈炼, 等. 核电站中气溶胶再悬浮的CFD研究[J]. 原子能科学技术, 2020, 54(5): 790-795. JIANG B, HUANG T, CHEN L, et al. CFD research on aerosol resuspension in nuclear power plant[J]. Atomic Energy Science and Technology, 2020, 54(5): 790-795. (in Chinese) |
| [11] |
陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001. TAO W Q. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2001. (in Chinese) |
| [12] |
周艳玲, 骆志平, 毕远杰, 等. 手套箱内粉末倾倒产生气溶胶的分布特性研究[J]. 中国辐射卫生, 2021, 30(2): 148-153, 164. ZHOU Y L, LUO Z P, BI Y J, et al. Study on the distribution characteristics of aerosol produced by powder dumping in glove box[J]. Chinese Journal of Radiological Health, 2021, 30(2): 148-153, 164. (in Chinese) |
| [13] |
昌旭东, 吴创新, 付广智. 通排风系统中239PuO2气溶胶微粒的流动特性[J]. 原子能科学技术, 2012, 46(2): 234-238. CHANG X D, WU C X, FU G Z. Flow characteristics of 239PuO2 aerosol particles in ventilating system[J]. Atomic Energy Science and Technology, 2012, 46(2): 234-238. (in Chinese) |
| [14] |
MANA Z. Étude sur la remise en suspension de particules suiteàla marche d'un opérateur[D]. Paris: Université Paris Sud-Paris XI, 2014.
|
| [15] |
宋妙发, 强亦忠. 核环境学基础[M]. 北京: 原子能出版社, 1999. SONG M F, QIANG Y Z. Fundamentals of nuclear environment[M]. Beijing: Atomic Energy Press, 1999. (in Chinese) |


