多自由度永磁电机利用永磁体和通电线圈之间的相互作用力驱动实现多自由度运动,其位姿测量是实现精确运动控制的关键。然而,多自由度运动的耦合性使测量变得更加复杂,因此研究精确、快速的多自由度电机位姿测量方法具有重要的实践意义。目前常用的测量方案按照检测原理可分为基于光电、基于惯性传感器和基于磁传感器等几类。
文[1-2]参考单自由度电机,使用3个垂直分布的光电编码器,实现三自由度位姿测量。文[3]通过多个光电编码环采集转子旋转时的颜色信号,检测转子的位姿。文[4]针对磁悬浮多自由度电机,提出了一种基于RGB颜色传感器的位姿检测方法。文[5]在转子上进行网格编码,利用视觉传感器进行位姿测量。基于光电的测量方法需要引入额外的复杂结构,每个传感器之间存在着微弱的耦合,且要求传感器和转子之间距离很小,容易产生碰撞。
文[6]利用陀螺仪传感器检测磁悬浮关节球形电机的位姿,通过姿态矩阵和位移积分算法获得转子位姿参数。文[7]采用双轴倾斜传感器和旋转编码器分别检测转子的三自由度位姿。基于惯性传感器的测量方法易产生误差累积,且需要在转子上安装测量单元,带来额外的惯性和动态不平衡。
基于磁传感器的位姿测量方法具有无额外机械结构、不惧遮挡、抗污染、测量范围大且灵敏度高的优点。文[8]利用多项式逼近法拟合永磁体磁场,然而测量精度不够理想。文[9]针对永磁体阵列采用曲面拟合方法得出姿态角的显式解。此类通过测量有限点的磁场并拟合出实际磁场的方法本身存在较大误差,拟合精度与稳定性存在矛盾,且计算量大,需要大量拟合点。
文[10]根据Biot-Savart定律得到永磁体的磁场分布,并假设实际磁场分布与理想分布成比例关系,由磁场方程组反解出位姿信息。文[11]将每个磁传感器与一个永磁体固结,利用永磁体分布式多极(DMP)方法对磁场进行建模,分别对转子的位置和位姿进行测量,位姿测量精度约为8°。文[12]利用DMP建立磁场模型,利用人工神经网络计算二自由度姿态。此类直接用磁场模型求解位姿的方法测量自由度有限,算法复杂,且对传感器的摆放位置有一定的要求,缺少通用性。
除了利用磁传感器,文[13]提出基于磁通模型的多自由度运动检测方法,通过线圈的感应电动势来计算转子的位姿。文[14-15]提出一种基于涡流传感器的球形电机三维旋转角测量方法。感应电动势法在高速时具有较高的信噪比,在低速或准静态时误差较大甚至难以工作。
本文提出了基于冗余磁场信息的三自由度电机位姿测量方法,利用多个磁传感器提高测量精度,无需额外结构和信息。通过最优化方法实现多自由度非接触绝对位姿测量,利用仿真数据和磁场线性模型,同时实现位姿测量和磁场模型标定,具有较好的通用性和测量精度。
1 问题描述本文主要针对图 1a的一种紧凑型永磁动铁式三自由度电机开展位姿测量方法研究及验证,并且能够很容易地拓展用于其他种类的多自由度永磁电机。本节首先介绍了所用电机的基本结构,然后分析了利用电机磁场进行位姿测量的难点并提出了问题需求。
|
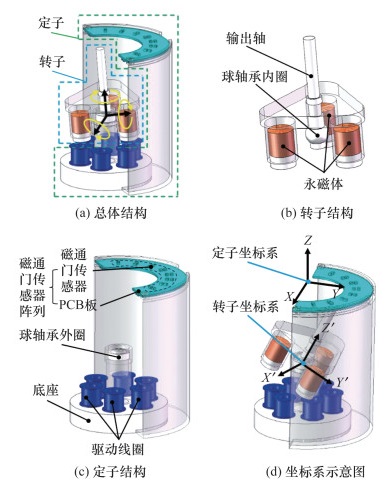
| 图 1 三自由度电机位姿测量系统 |
图 1a中的电机定子和转子通过球轴承内外圈之间形成的球面副实现三自由度旋转。图 1b显示了其定子上3个轴向充磁的相同圆柱永磁体,其产生的磁场既为电机线圈提供驱动所需安培力,同时也作为转子位姿测量基准磁场;图 1c为电机定子结构,电机底部基座定子安装有6个驱动线圈,顶部由16个磁通门传感器(FMS)组成的磁通门传感器阵列(FMSA)与定子基座固联,检测电机三自由度运动时所处位置的磁感应强度变化。
在本文的测量方法中,FMSA具有高度集成性,且对传感器的布置无特殊要求,可根据电机形状灵活布置。同时,磁通门传感器体积小巧,与其他磁传感器相比,可以实现更紧凑的设计。
利用磁传感器测量电机位姿的基本原理是电机在运动过程中,永磁体与磁传感器的相对位置发生变化,引起磁传感器检测信号发生相应的变化,由此磁传感器信号中包含了电机位姿信息,设两者之间的数学关系为
| $ \boldsymbol{B}=\boldsymbol{F}(\boldsymbol{\theta}) . $ | (1) |
其中:
通过磁场建模得到F后,根据式(1)由已知的检测信号与模型的逆解算出电机位姿为
| $ \boldsymbol{\theta}=\boldsymbol{F}^{-1} \boldsymbol{\beta} . $ |
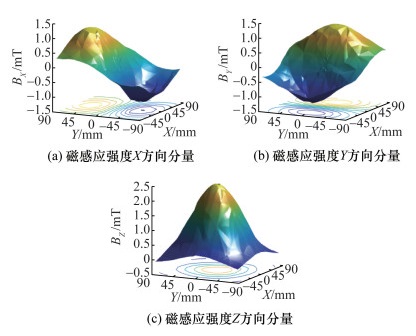
由上可知,实现精确位姿解算的关键在于准确建立F。由于永磁体所产生的磁场强度空间分布具有极强的非线性,准确建立F较为困难,为了说明这一点,图 2给出了使用Maxwell 16.0软件得到的FMSA所在平面(XY平面)的标称磁感应强度各分量。尽管对于一般圆柱形永磁体磁场,可以通过分子电流模型和Biot-Savart定律得到多重积分形式的理论数学模型。然而由于多重积分计算量大等原因,难以直接基于这种理论模型进行高精度实时位姿解算。因此,一种高效、精确的磁场建模及其解算方法是实现基于磁场信息的多自由度电机位姿测量的关键。
|
| 图 2 FMSA平面标称磁感应强度分布图 |
2 方法原理
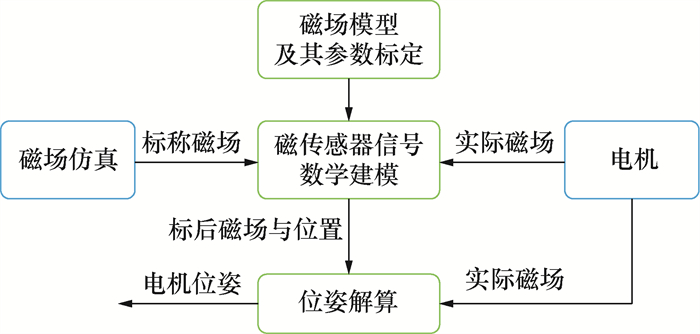
所提方法基本原理如图 3所示,主要包含磁场模型及其参数标定、磁传感器信号数学建模和位姿解算3个步骤。
|
| 图 3 基本原理图 |
2.1 磁场模型及其参数标定
首先根据分子电流模型和Biot-Savart定律可以建立圆柱形永磁体磁场的理论数学模型[16],空间中任一点(x, y, z)处磁感应强度3个方向的分量为
| $ \left\{\begin{align*} B_{x}= & \frac{B_{\gamma}}{4 \pi} \int_{0}^{h_{0}} \int_{0}^{2 \pi} \frac{d_{0}\left(z-z_{0}\right) \cos \varphi}{2 M} \mathrm{~d} \varphi \mathrm{~d} z_{0}, \\ B_{y}= & \frac{B_{\gamma}}{4 \pi} \int_{0}^{h_{0}} \int_{0}^{2 \pi} \frac{d_{0}\left(z-z_{0}\right) \sin \varphi}{2 M} \mathrm{~d} \varphi \mathrm{~d} z_{0}, \\ B_{z}= & \frac{B_{\gamma}}{4 \pi} \int_{0}^{h_{0}} \int_{0}^{2 \pi} \frac{d_{0}\left(y-\frac{d_{0}}{2} \sin \varphi\right) \sin \varphi-d_{0}\left(x-\frac{d_{0}}{2} \cos \varphi\right) \cos \varphi}{2 M} \mathrm{~d} \varphi \mathrm{~d} z_{0}, \\ & M=\left[\left(x-\frac{d_{0}}{2} \cos \varphi\right)^{2}+\left(y-\frac{d_{0}}{2} \sin \varphi\right)^{2}+\left(z-z_{0}\right)^{2}\right]^{\frac{3}{2}} . \end{align*}\right. $ | (2) |
其中:bγ为永磁体的标称剩余磁化强度,h0为永磁体的标称高度,d0为永磁体的标称半径,z0和φ为积分参数。由圆柱形永磁体理论模型可知其标称磁场的空间分布主要受设计时的永磁体标称参数(h0、d0和Bγ)的影响。
理论上,永磁体标称参数代入上述理论数学模型即可得到准确磁场分布。然而永磁体的实际物理值并不与设计时的标称参数值一致,直接将标称参数值用于磁场模型数值模型计算得到标称磁场并将其用于位姿解算,可能带来不可接受的位姿测量误差,因此还需要探讨参数的标定方法。
由式(2)可知永磁体剩磁大小与空间磁场任意位置分布的磁敏感传感器输出信号都是线性关系,因此可以视为比例系数K。对于永磁体实际高度h和实际直径d,虽然其对磁感应强度大小的影响是非线性的,这使得它们的实际值难以通过实际磁场分布精确标定,尽管如此,在一定机械加工与充磁要求的实际条件下,实际与标称磁场分布之间的差异非常微小,这使得磁感应强度大小与参数间的线性关系近似成立。由此,下面给出基于这种思路的一种标称参数偏移值标定方法。
设永磁体参数的实际值和标称值之间的偏移分别为Δh与Δd,对标称磁场在其邻域内进行线性展开:
| $ \begin{align*} & \boldsymbol{B}\left(h_{0}+\Delta h, d_{0}+\Delta d, x, y, z\right)= \\ & \boldsymbol{B}\left(h_{0}, d_{0}, x, y, z\right)+\left.\frac{\partial \boldsymbol{B}}{\partial h}\right|_{h_{0}} \Delta h+ \\ & \left.\frac{\partial \boldsymbol{B}}{\partial d}\right|_{d_{0}} \Delta d+O\left(\Delta h^{2}, \Delta d^{2}, \Delta h \Delta d\right). \end{align*} $ | (3) |
其中O(Δh2, Δd2, ΔhΔd)为未建模高阶小量,偏导数项在数值计算过程中可以由差分近似得到,即
| $ \left\{\begin{array}{l} \left.\frac{\partial \boldsymbol{B}}{\partial h}\right|_{h_{0}} \approx \frac{\boldsymbol{B}\left(h_{0}+\Delta h_{\mathrm{s}}, d_{0}, x, y, z\right)-\boldsymbol{B}\left(h_{0}, d_{0}, x, y, z\right)}{\Delta h_{\mathrm{s}}}=\frac{\Delta \boldsymbol{B}_{h}}{\Delta h_{\mathrm{s}}}, \\ \left.\frac{\partial \boldsymbol{B}}{\partial d}\right|_{d_{0}} \approx \frac{\boldsymbol{B}\left(h_{0}, d_{0}+\Delta d_{\mathrm{s}}, x, y, z\right)-\boldsymbol{B}\left(h_{0}, d_{0}, x, y, z\right)}{\Delta d_{\mathrm{s}}}=\frac{\Delta \boldsymbol{B}_{d}}{\Delta d_{\mathrm{s}}} . \end{array}\right. $ | (4) |
其中:Δhs和Δds为参数差分步长,ΔBh和ΔBd为磁场分布的差分项,可通过理论或数值模型计算得到。将式(4)代入式(3),得到标定后的磁场为
| $ \boldsymbol{B}=\left(\boldsymbol{B}_{0}+\frac{\Delta h}{\Delta h_{\mathrm{s}}} \Delta \boldsymbol{B}_{h}+\frac{\Delta d}{\Delta d_{\mathrm{s}}} \Delta \boldsymbol{B}_{d}\right) K . $ | (5) |
式(5)考虑了永磁体在制造过程中的充磁误差以及尺寸误差,即为所建立的磁场参数模型。
2.2 磁传感器信号数学建模图 1d中,为利用传感器的冗余磁场信息求解电机转子位姿,本文通过空间变换矩阵将所有传感器磁场信号转换到转子坐标系,从而建立位姿测量数学模型。
假设FMSA的各传感器位于同一平面,则可设立传感器安装参数:
| $ \begin{gathered} \boldsymbol{P}_{i}=\left(\begin{array}{llll} x_{i} & y_{i} & 0 & 1 \end{array}\right)^{\mathrm{T}}, \quad \boldsymbol{n}_{i}=\left[\begin{array}{llll} \cos \theta_{i} & \sin \theta_{i} & 0 & 1 \end{array}\right]^{\mathrm{T}}, \\ i=1, 2, \cdots, 16 . \end{gathered} $ |
其中:Pi为传感器i在定子坐标系中的位置,ni为传感器i的敏感方向向量。从转子坐标系到定子坐标系的三维旋转变换矩阵R和平移变换矩阵T为
| $ \begin{array}{l} \boldsymbol{R}=&\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha & 0 \\ 0 & -\sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} \cos \beta & 0 & -\sin \beta & 0 \\ 0 & 1 & 0 & 0 \\ \sin \beta & 0 & \cos \beta & 0 \\ 0 & 0 & 0 & 1 \end{array}\right] \cdot \\ &{\left[\begin{array}{cccc} \cos \gamma & \sin \gamma & 0 & 0 \\ -\sin \gamma & \cos \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]} ,\\ &\;\;\;\;\;\;\;\;\;\;\;\;\boldsymbol{T}=\left[\begin{array}{cccc} 1 & 0 & 0 & x_{\mathrm{T}} \\ 0 & 1 & 0 & y_{\mathrm{T}} \\ 0 & 0 & 1 & z_{\mathrm{T}} \\ 0 & 0 & 0 & 1 \end{array}\right]. \end{array} $ |
其中:α、β和γ分别为转子绕X、Y和Z轴旋转的旋转角即转子位姿角;xT、yT和zT为转子坐标系未旋转时定子坐标系原点在转子坐标系中的坐标,即转子相对于FMSA的安装位置,为待标定参数,在位姿测量之前进行标定。标定后传感器在转子坐标系中的初始位置参数为
| $ \boldsymbol{P}_{i}^{\prime}=\boldsymbol{T} \boldsymbol{P}_{i}=\left(\begin{array}{llll} x_{i}+x_{\mathrm{T}} & y_{i}+y_{\mathrm{T}} & z_{\mathrm{T}} & 1 \end{array}\right)^{\mathrm{T}} . $ |
由式(5)可知电机在转子坐标系中的标后磁场分布为B(x, y, z),包含磁场待标定参数Δh、Δd、K。传感器i敏感方向上的磁感应强度为B(xi+xT, yi+yT, zT)·ni,考虑“旋转”变换后传感器i敏感方向上的磁感应强度为
| $ \begin{gathered} f_{i}(\boldsymbol{X}, \boldsymbol{Q})=\boldsymbol{B}\left(x_{i}^{\prime}, y_{i}^{\prime}, z_{i}^{\prime}\right) \cdot \boldsymbol{R}(\alpha, \beta, \gamma) \boldsymbol{n}_{i}, \\ \left(x_{i}^{\prime} y_{i}^{\prime} z_{i}^{\prime} 1\right)^{\mathrm{T}}=\boldsymbol{R}(\alpha, \beta, \gamma) \boldsymbol{P}_{i}^{\prime} . \end{gathered} $ |
其中:
令传感器i检测的实际磁感应强度信号为Bmi,对应检测噪声为εi,得到传感器i的信号模型为
| $ B_{\mathrm{m} i}=f_{i}(X, Q)+\varepsilon_{i} . $ | (6) |
X为从该模型中由传感器信号解算出的电机位姿,需要将式(6)视为关于位姿X的非线性方程组,接下来给出该方程组的解算方法。
2.3 位姿解算方法先假设Q已知,推导位姿解算方法,令e=(ε1 ε2 … ε16)T,则可将式(6)改写为
| $ \boldsymbol{B}=\boldsymbol{F}_{1}(\boldsymbol{X})+\boldsymbol{e} . $ |
假设其有一个近似解Xk,对F1(X)在Xk处进行Taylor展开(忽略非线性项),得到
| $ \begin{gather*} \boldsymbol{B}=\boldsymbol{F}_{1}\left(\boldsymbol{X}^{k}\right)+\boldsymbol{J}\left(\boldsymbol{X}^{k}\right)\left(\boldsymbol{X}-\boldsymbol{X}^{k}\right)+\boldsymbol{e} \\ \boldsymbol{J}\left(\boldsymbol{X}^{k}\right)=\left.\frac{\partial \boldsymbol{F}_{1}}{\partial \boldsymbol{X}}\right|_{\boldsymbol{x}=\boldsymbol{x}^{k}} \end{gather*} $ | (7) |
将式(7) 看作一个无约束最优化问题, 根据最小二乘法, 需要求解
| $ \begin{align*} \boldsymbol{X}^{k+1}= & \boldsymbol{X}^{k}+\left[\boldsymbol{J}^{\mathrm{T}}\left(\boldsymbol{X}^{k}\right) \boldsymbol{J}\left(\boldsymbol{X}^{k}\right)\right]^{-1} \boldsymbol{J}^{\mathrm{T}}\left(\boldsymbol{X}^{k}\right) \cdot \\ & {\left[\boldsymbol{B}-\boldsymbol{F}_{1}\left(\boldsymbol{X}^{k}\right)\right] . } \end{align*} $ | (8) |
利用传感器检测信号和Pi与ni,在给定位姿的初值X0后进行迭代,直到相邻2次迭代结果之差小于阈值或迭代次数达到最大值时停止迭代,并以此时迭代结果作为位姿的测量值。
迭代计算的初值须确保位于收敛域内,由文[17]可知式(8)的收敛域为其真值解附近的一个邻域,考虑到电机运动的连续性,将上一测量时刻的位姿解算值作为下一测量时刻的迭代初值,则当相邻2次位姿解算时间充分短时,解算结果相差足够小,从而使得该迭代初值始终位于迭代收敛域内,实现连续实时地运动测量。
在实际位姿测量前还需对Q进行标定,类似式(8),可以推导出含待标定参数的磁传感器信号模型迭代公式为
| $ \boldsymbol{Y}^{k+1}=\boldsymbol{Y}^{k}+\left[\boldsymbol{J}^{\mathrm{T}}\left(\boldsymbol{Y}^{k}\right) \boldsymbol{J}\left(\boldsymbol{Y}^{k}\right)\right]^{-1} \boldsymbol{J}^{\mathrm{T}}\left(\boldsymbol{Y}^{k}\right)\left[\boldsymbol{B}-\boldsymbol{F}_{2}\left(\boldsymbol{Y}^{k}\right)\right] $ | (9) |
其中Y=(X Q),如此按照式(9)的方法可以解算Y,同时实现位姿测量和参数标定。
3 仿真结果为验证所提方法的有效性并测试其性能,分别进行了电机位姿测量仿真与磁场模型参数标定仿真。
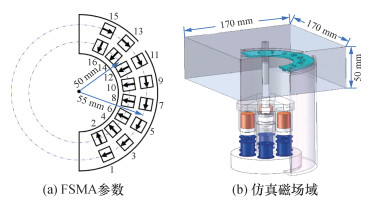
3.1 位姿测量仿真为方便实验,不妨设置FMSA的参数如图 4a,内圈FMS测量径向磁场,外圈FMS测量周向磁场。图 4b中,仿真磁场范围设定为170×170×60 mm的长方体空间,本小节仅对位置参数进行标定。
|
| 图 4 FSMA与磁场仿真参数示意图 |
在磁传感器信号中引入均值μ=0,方差σ=0.106 μT2的Gauss随机量,模拟实际中的检测噪声。
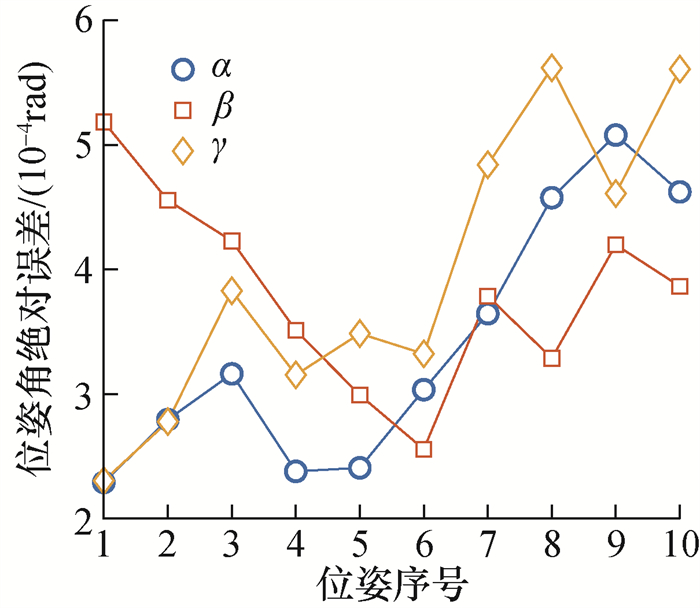
先假定磁场模型参数不存在偏差,电机的初始位姿设为X=(0.01 0.01 0.01)T, 待标定位置参数真实值设为Q=(-4 1 76)T,进行位置参数标定时式(9)的迭代初值设定为Y0=(0 0 0 0 0 80)T,位置参数标定结果如表 1所示。位姿测量时电机位姿各自由度等步长变化,每次增加0.03 rad,位置不变,由此针对10个位姿进行测量仿真,每个仿真50次后得到位姿平均测量误差如图 5所示。
| 类别 | xT/mm | yT/mm | zT/mm |
| 真实值 | 4.000 | 1.000 | 76.000 |
| 标定值 | 3.967 | 1.011 | 76.009 |
| 误差 | 0.033 | 0.011 | 0.009 |
|
| 图 5 磁场模型参数无偏差时的位姿测量仿真结果 |
表 1和图 5表明,在磁场模型参数无偏差、磁传感器信号信噪比为68 dB的条件下,位置标定的绝对误差小于0.04 mm,位姿测量的绝对误差小于6×10-4 rad。
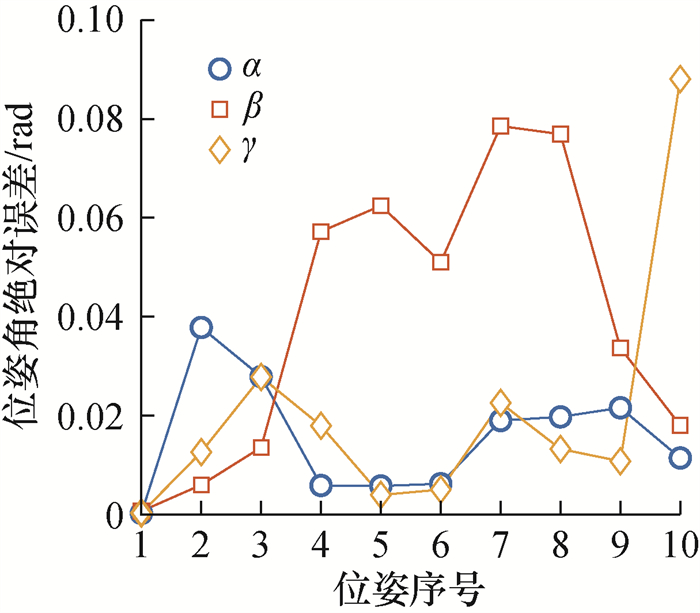
然而永磁体参数的实际和标称值之间必然存在偏移,在此假定K存在5%偏移,Δh和Δd均存在5 μm偏移,其他仿真参数不变时,仿真得到的位置参数标定结果如表 2所示,位姿平均测量误差如图 6所示。
| 类别 | xT/mm | yT/mm | zT/mm |
| 真实值 | 4.000 | 1.000 | 76.000 |
| 标定值 | 3.957 | 1.010 | 76.011 |
| 误差 | 0.043 | 0.010 | 0.011 |
|
| 图 6 磁场模型参数有偏差时的位姿测量仿真结果 |
由表 2和图 6可见,当K仅存在5%偏移,Δh和Δd均仅存在5 μm偏移时,相比参数无偏差时,位置标定误差变化较小,但位姿测量绝对误差增加了100多倍。因此,对磁场模型进行标定是必要的。
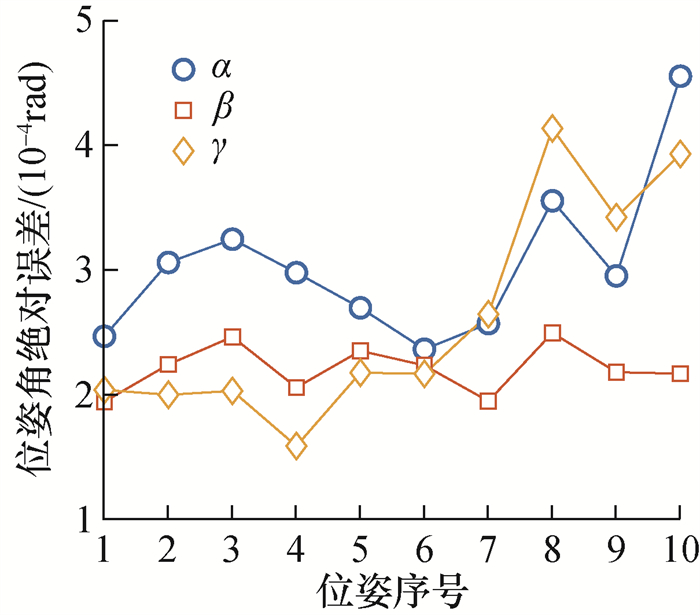
3.2 磁场模型参数标定仿真保持其他仿真条件与3.1节相同,利用2.3节的式(9)对图 6所示仿真中的永磁体参数偏移进行标定,参数标定结果如表 3所示。将标定后的磁场模型代入式(5)磁传感器信号模型中,进行位姿测量仿真,10次位姿测量仿真结果如图 7所示。
| 类别 | K | |||||
| 真实值 | 4.000 | 1.000 | 76.000 | 5.000 | 5.000 | 0.950 |
| 标定值 | 3.986 | 1.001 | 76.021 | 5.098 | 4.993 | 0.949 |
| 误差 | 0.014 | 0.001 | 0.021 | 0.098 | 0.007 | 0.001 |
|
| 图 7 永磁体参数偏移标定后的位姿测量仿真 |
与图 6对比可知,进行永磁体参数偏移标定后的位姿测量误差减少至未标定时的约1%。仿真结果说明经过磁场模型参数标定,由实际永磁体制造偏差所引起的位姿测量误差得到了补偿。
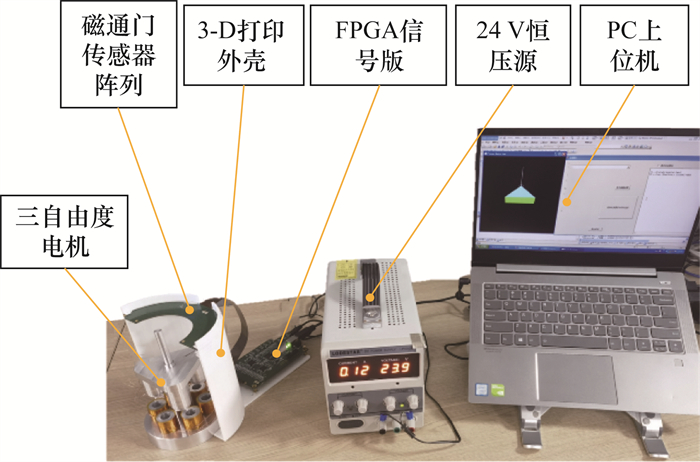
4 实验方案与结果 4.1 实验平台搭建的三自由度永磁电机位姿测量实验平台整体如图 8所示。电机固定于支架和FMSA的圆心处,FMSA通过螺钉和凹槽固定在外壳的圆柱面上,信号处理电路板搭载1块高性能FPGA(Xilinx公司XC3S1600E-4FG320) 进行磁传感器信号采集与处理。信号处理板与FMSA间通过柔性信号线连接,电源提供24V恒定电压。FPGA信号板对FMSA的磁场数据进行采样和信号处理后通过UART串口通信将磁场数据发送给PC上位机。上位机中利用Windows下的Win32子程序负责线程接收数据,RTX实时操作系统下的RTSS实时子程序实现精准、稳定定时,实时解算位姿,并将求解位姿结果实时显示于窗口。
|
| 图 8 实验平台示意图 |
4.2 磁场与位置参数标定实验
初步测量得到永磁体的剩磁在-500 000 A/m2左右,利用第2章的磁场模型和位置参数标定方法得到的参数标定结果为xT=-3.855 mm、yT=2.036 mm、zT=76.512 mm、Δh=0.130 μm、Δd=-9.320 μm和K=1.017。
分别利用标定前后的磁场模型进行电机位姿测量,随机3个位姿下16个传感器测量磁场与对应标定后磁场的残差平方和如表 4所示。
可见,标定后磁场偏移有较大下降,约为标定前的22%。
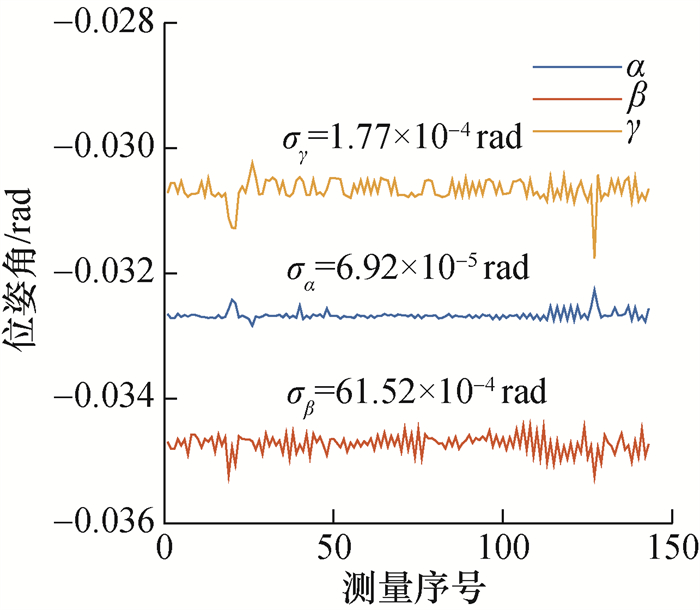
4.3 稳定性实验进行稳定性实验测定所提方法位姿测量的分辨率。实验中电机保持静止一段时间,位姿角的测量结果和标准差如图 9所示。
|
| 图 9 电机静止时的位姿测量结果 |
综合图 9中的σα、σβ和σγ可知,所提方法的位姿角测量分辨率不大于1.77×10-4 rad即0.01°。
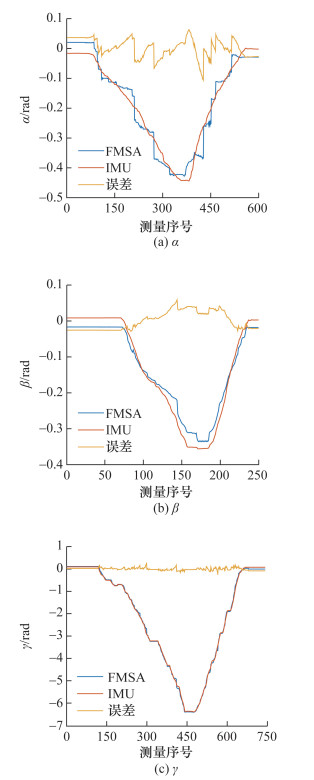
4.4 位姿测量对比实验将所提方法与市面上常见的可测量三自由度旋转角的惯性传感器IMU (辰翼电子科技IM600)进行对比实验。FMSA和IMU的测量频率均设定为20 Hz,最终的位姿测量结果如图 10所示。
|
| 图 10 位姿角测量对比实验结果 |
由图 10可见,所提方法的测量结果与IMU的测量结果基本吻合,由于环境噪声等因素,导致两者误差存在一定的波动。α、β和γ的均方根误差(RMSE)分别为0.031、0.025和0.056 rad。
5 结论本文提出了一种基于冗余磁场信息的三自由度电机位姿测量方法,利用多个磁传感器提高测量精度,通过最优化方法实现多自由度位姿测量;利用仿真数据和磁场线性模型,实现磁场模型标定。相比其他方法,该方法可以实现非接触实时绝对位姿测量,且结构紧凑,灵敏度高,在位姿测量的同时实现FMSA的安装位置测量以及永磁体参数偏移标定,具有较好的通用性。在自主搭建的RTX实时操作系统和Windows软件平台、FMSA和FPGA硬件平台的物理系统上,进行了永磁体参数偏移标定实验、稳定性实验和对比实验,验证了基于Gauss-Newton法的电机位姿测量算法和基于线性展开的磁场参数标定方法的可行性。
为了避免漏磁和磁饱和现象对电机磁场的影响,在实际应用中,电机结构应尽量使用非磁性或弱磁性材料如铝合金。对于必须使用铁磁性材料的部件如轴承,可以采取磁屏蔽措施,以减少其对测量精度的影响。
未来还将进行FMSA拓扑结构的优化设计,以及利用冗余磁场信息实现传感器参数的自标定等,提高传感器检测的磁感应强度和传感器处的磁场梯度,从而进一步提高测量稳定性和测量精度。
| [1] |
LEE K M, ROTH R B, ZHOU Z. Dynamic modeling and control of a ball-joint-like variable-reluctance spherical motor[J]. Journal of Dynamic Systems, Measurement, and Control, 1996, 118(1): 29-40. DOI:10.1115/1.2801148 |
| [2] |
LEE K M, KWAN C K. Design concept development of a spherical stepper for robotic applications[J]. IEEE Transactions on Robotics and Automation, 1991, 7(1): 175-181. DOI:10.1109/70.68082 |
| [3] |
王群京, 雍爱霞, 陈丽霞, 等. 一种永磁球形步进电机转子位置的检测方法[J]. 中国电机工程学报, 2006, 26(22): 92-96. WANG Q J, YONG A X, CHEN L X, et al. A kind of method of measuring the rotor position of permanent magnetic spherical stepper motor[J]. Proceedings of the CSEE, 2006, 26(22): 92-96. (in Chinese) |
| [4] |
朱忠捷. 基于光电检测技术磁悬浮球形主动关节转子位姿检测系统的设计与研究[D]. 扬州: 扬州大学, 2018. ZHU Z J. Design and research of magnetic levitation spherical active joint rotor pose detection system based on photoelectric detection technology [D]. Yangzhou: Yangzhou University, 2018. (in Chinese) |
| [5] |
GARNER H, KLEMENT M, LEE K M. Design and analysis of an absolute non-contact orientation sensor for wrist motion control [C]//Proceedings of 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Como, Italy: IEEE, 2001: 69-74.
|
| [6] |
张小红. 磁悬浮球形主动关节转子检测系统的设计与研究[D]. 扬州: 扬州大学, 2016. ZHANG X H. Design and research of magnetic levitation spherical active joint rotor detection system [D]. Yangzhou: Yangzhou University, 2016. (in Chinese) |
| [7] |
李丹. 直流永磁球形电机位置检测的关键技术研究[D]. 芜湖: 安徽工程大学, 2013. LI D. Key technology research on position of detection method for DC permanent magnet spherical motor [D]. Wuhu: Anhui Polytechnic University, 2013. (in Chinese) |
| [8] |
李争, 王欣欣, 张玥. 基于分布式多极磁场模型的永磁多自由度电机位置检测方法研究[J]. 微电机, 2014, 47(3): 37-42, 55. LI Z, WANG X X, ZHANG Y. Position detection of PM M-DOF actuators based on distributed magnetic field multipole models[J]. Micromotors, 2014, 47(3): 37-42, 55. DOI:10.3969/j.issn.1001-6848.2014.03.009 (in Chinese) |
| [9] |
YAN L, ZHU B, JIAO Z X, et al. An orientation measurement method based on hall-effect sensors for permanent magnet spherical actuators with 3D magnet array[J]. Scientific Reports, 2014, 4(1): 6756. DOI:10.1038/srep06756 |
| [10] |
李争, 郭曼洁, 马骏. 基于等效电流模型的永磁多自由度电机位置检测方法的研究[J]. 电机与控制应用, 2015, 42(5): 42-47. LI Z, GUO M J, MA J. Magnetic field and position detection of PM actuators based on equivalent current model[J]. Electric Machines & Control Application, 2015, 42(5): 42-47. (in Chinese) |
| [11] |
李雪逸, 王群京, 钱喆, 等. 一种球形电动机转子三自由度位置检测方法研究[J]. 微特电机, 2019, 47(2): 12-17. LI X Y, WANG Q J, QIAN Z, et al. Novel three-DOF position detection method for permanent magnet spherical motor rotor[J]. Small & Special Electrical Machines, 2019, 47(2): 12-17. (in Chinese) |
| [12] |
KIM J, SON H. Two-DOF orientation measurement system for a magnet with single magnetic sensor and neural network [C]//Proceedings of 201714th International Conference on Ubiquitous Robots and Ambient Intelligence. Jeju, Korea (South): IEEE, 2001: 448-453.
|
| [13] |
BAI K, LEE K M, LU J J. A magnetic flux model based method for detecting multi-DOF motion of a permanent magnet spherical motor[J]. Mechatronics, 2016, 39: 217-225. DOI:10.1016/j.mechatronics.2016.06.001 |
| [14] |
YANG L, HU P H, MA K L, et al. A new method for measuring 3D rotation angle of spherical joint[J]. Measurement, 2022, 190: 110661. DOI:10.1016/j.measurement.2021.110661 |
| [15] |
HU P H, ZHAO L C, TANG C X, et al. A new method for measuring the rotational angles of a precision spherical joint using eddy current sensors[J]. Sensors, 2020, 20(14): 4020. DOI:10.3390/s20144020 |
| [16] |
周恩权, 郑仲桥, 张燕红, 等. 圆柱形永磁体磁场建模及仿真研究[J]. 河南科技, 2017(21): 139-143. ZHOU E Q, ZHENG Z Q, ZHANG Y H, et al. Modeling and simulation for cylinder permanent magnetic field[J]. Henan Science and Technology, 2017(11): 139-143. (in Chinese) |
| [17] |
CHEN J H, LI W G. Convergence of Gauss-Newton's method and uniqueness of the solution[J]. Applied Mathematics and Computation, 2005, 170(1): 686-705. |



