2. 清华大学 先进成形制造教育部重点实验室, 北京 100084;
3. 中国人民解放军32555部队, 广州 510730
2. Key Laboratory for Advanced Materials Processing Technology of Ministry of Education, Tsinghua University, Beijing 100084, China;
3. The 32555th Unit of the People's Liberation Army of China, Guangzhou 510730, China
旋转摩擦焊(rotary friction welding, RFW)是一种固相热压焊方法,作为摩擦焊技术最早出现的工艺形式,能够获得高质量的接头,被广泛地应用于同种或异种材料的连接中。RFW驱动两个待连接工件的接合面在轴向(法向)压力下进行高速旋转运动,通过摩擦产生的热量使其界面及邻域达到热塑性状态,再迅速加压顶锻,通过界面的原子扩散和再结晶将被焊工件连接成为一体[1]。RFW主要包含连续驱动摩擦焊和惯性摩擦焊两类驱动形式。RFW涉及复杂的热、力和冶金过程,其产热过程在强烈的热力耦合作用下进行,摩擦界面的力和温度演化历程影响焊接接头的组织演变和力学性能[2-3]。例如,在一定范围内的轴向压力增加通常会在焊缝中产生更多精细、等轴化的再结晶晶粒结构,使得接头的显微硬度和抗拉强度上升,并改善焊接接头力学性能的径向差异[4]。同时,热输入量和冷却速率直接影响焊缝组织,从而改变接头性能[5]。总之,接头的应力-温度关系影响RFW获得的接头性能[6]。
摩擦焊研究的重点之一在于深入探索热力耦合的机制和过程,获得焊接过程的力和温度演化历程,从而为工艺参数和接头组织调控提供指导。RFW过程中存在高速旋转和显著塑性变形,仅通过实验手段无法直接获得焊接中的温度演化和塑性变形过程。同时,由于摩擦焊全过程是物理非线性、几何非线性的,难以建立解析模型和获得准确解[7-8],因此数值模拟成为摩擦焊理论研究的主要方法。随着计算技术的发展,产生了一系列数值模拟方法,进一步揭示了RFW过程中各物理场的演化规律,为其热力耦合行为的理论研究提供了有力支撑。
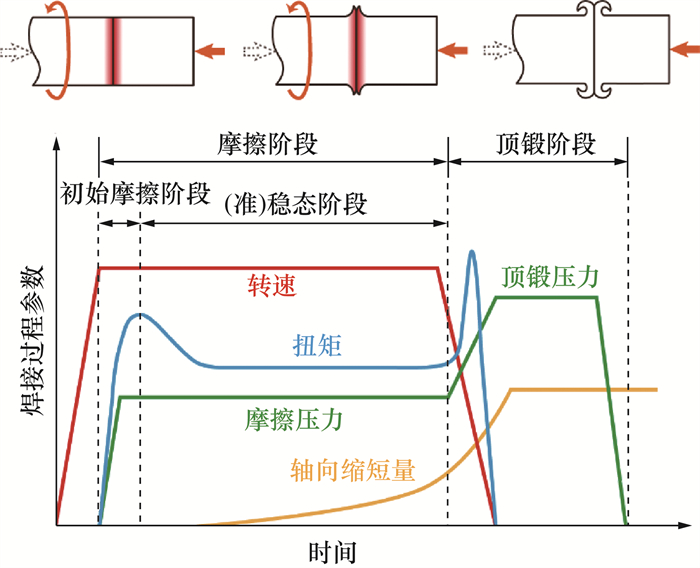
1 旋转摩擦焊热力耦合行为 1.1 摩擦焊过程的摩擦理论RFW包括摩擦和顶锻2个主要阶段,摩擦阶段又分为初始摩擦阶段和(准)稳态阶段,如图 1所示。在初始摩擦阶段,一侧工件高速旋转,同时另一侧工件水平移动,使工件表面接触挤压,界面上不平整的凸起首先接触摩擦。随着摩擦产热过程的进行,实际接触面积不断扩大,摩擦扭矩迅速升高,产生一个初始峰值[9]。同时,界面及其邻域温度逐渐上升,使得金属塑性区面积增加,摩擦界面逐渐被高温黏塑性金属覆盖,相对运动由界面摩擦转变为黏塑性金属层内部剧烈的塑性变形。在摩擦压力的进一步作用下,高温黏塑性金属发生动态再结晶(dynamic recrystallization, DRX),流动应力降低,摩擦扭矩在到达前峰值后下降。随着产热积累和轴向热传导的进行,黏塑性金属层逐渐变宽,焊核区金属沿径向塑性流动并被挤出,形成飞边[10]。随着摩擦持续,摩擦扭矩进入稳定状态,基本保持恒定,轴向缩短量逐渐变大,高温区变宽,飞边增大。这一阶段通常被称为稳态或准稳态阶段。当轴向缩短量或摩擦时间到达设定值后,进入顶锻阶段。旋转工件刹车制动,同时施加一个大于摩擦阶段压力的顶锻压力,并保压一段时间。此时,轴向缩短量急剧增加,界面温度迅速下降,金属流动性降低,出现第2个峰值扭矩,即后峰值。焊核区金属继续发生相互扩散和再结晶,最终形成冶金结合的接头。
|
| 图 1 RFW过程参数随时间变化示意图 |
探究摩擦焊过程中的热力耦合行为是研究摩擦焊接头形成机理的基础。热力耦合行为直接影响界面产热和接头区温度分布,决定了焊接所需功率、扭矩和界面剪切力。尽管摩擦学中已有丰富成熟的理论,但与常规摩擦条件下的摩擦行为不同,摩擦焊过程为持续接触摩擦,不仅有滑动摩擦,还涉及高温下的塑性变形和材料流动[11]。Bowden等[12]在1949年提出了黏着摩擦理论,即黏着-剪切-犁沟理论,被广泛接受。这一理论认为,焊接界面在轴向压力作用下发生接触时,局部凸起的接触点受到较大压力,发生塑性屈服和塑性流动,使接触点牢固结合,称为黏着;当界面进行相对运动时,黏着点发生剪切;若两界面存在硬度差异,硬度较大界面上的微小凸起会在运动过程中在硬度较低的焊件界面上刻划,产生犁沟;上述过程反复进行,产生摩擦力和剪切变形。
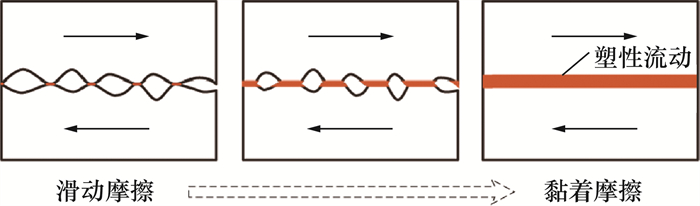
基于黏着摩擦理论,通过研究焊接过程中扭矩的变化规律,Hasegawa等[13]和Kimura等[14]结合大量实验证明,随着摩擦过程的进行,界面局部主导的摩擦机制逐渐从滑动摩擦转变为黏着摩擦,温度和应变率则决定了摩擦界面在径向分布的摩擦机制的不同。目前普遍认为,摩擦焊主要包括3种摩擦行为:滑动(slide)摩擦、黏着(stick)摩擦和滑动-黏着(slide-stick)摩擦。不同性质的摩擦行为在摩擦焊的热分析中意味着不同的产热机制和边界条件。滑动摩擦通常被认为是传统的Coulomb摩擦,遵循Coulomb摩擦定律,作为面热源向焊核区提供热量;黏着摩擦则关注变形体内部的塑性变形产热,即能量耗散,是存在于黏塑性金属层内部的内热源;而滑动-黏着摩擦本质仍是滑动和黏着摩擦在时间、空间的过渡,如图 2所示。在实际焊接时,滑动和黏着两个摩擦阶段并没有明确转折,因此如何准确定义这两种摩擦机制在局部的过渡是建立摩擦焊产热模型的一个关键问题。
|
| 图 2 滑动摩擦向黏着摩擦转变示意图 |
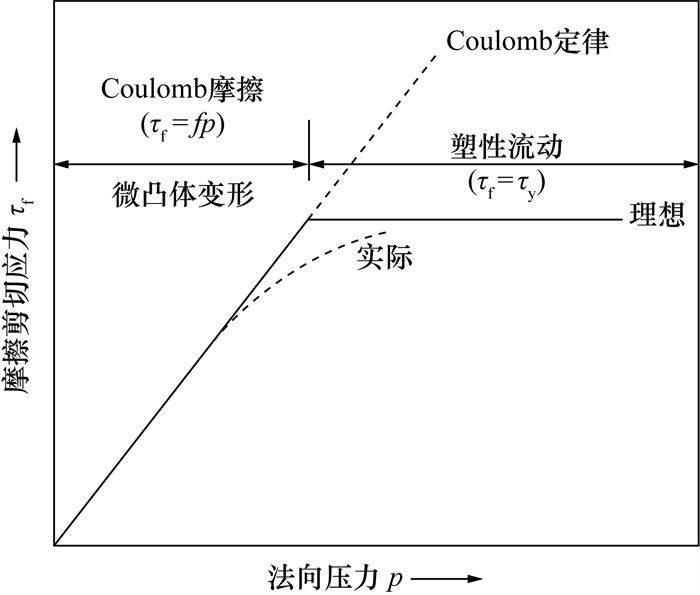
Moal和Massoni[15]曾提出滑动和黏着两个阶段中摩擦剪切应力的演化依赖于相对旋转速度。Maalekian等[16]则认为,当接触剪应力小于剪切屈服应力时,满足滑动条件,根据黏着摩擦理论,此时实际接触面积占表观接触面积的一部分,摩擦力与法向压力成正比;当实际接触面积和表观接触面积近似相等时,界面处完全发生塑性流动,摩擦应力与材料剪切力相等,满足黏着条件,如图 3所示。图中:τf为摩擦剪应力,τy为剪切屈服应力。Maalekian等[16]认为转变温度约为0.6Tm(Tm为熔点),即DRX温度附近,只依赖材料的性质和温度。尽管这一理论忽视了界面上径向产热的不均匀性,但在模型计算中的合理性和有效性使其至今仍被广泛接受[17]。李京龙等[18]引入了摩擦阻抗的概念,将滑动和黏着摩擦过程中的产热统一表述为摩擦阻抗做功,滑动摩擦阻抗产热的热强较低,仅起预热作用,黏着阻抗则起到主导作用。对于RFW,摩擦阻抗由滑动摩擦向黏着摩擦顺序演变,摩擦初期以(1/3)R0~(2/3)R0(R0为工件半径)之间的某环状区域的滑动摩擦为主导;当温度升高至一定程度后,形成塑性金属环,随后塑性环逐渐向内、向外生长,完成滑动摩擦向黏着摩擦的转变过渡。Wang等[19]提出了一种通过最大熵产生原理(maximum entropy production principle, MEPP)得到摩擦机制转变判据的方法。MEPP是指在一定约束条件下,远离平衡的开放体系会向熵产生率最大的方向演化。由于摩擦焊涉及机械能向热能的转化和飞边的挤出,是包含能量和物质输入、输出的开放体系,是一种非线性、非平衡的不可逆热力学过程(或耗散结构)[20]。MEPP表明,非平衡系统的熵产生率具有由其边界条件决定的最大值,为研究不同动态过程的耦合提供了一个简单而有效的热力学判据或框架。通过分别计算滑动摩擦和黏塑性变形阶段下摩擦界面的熵产生率θf和θp,从滑动摩擦状态到黏塑性变形状态的过渡准则可以表示为
| $ \theta_{\mathrm{f}} \leqslant \theta_{\mathrm{p}} . $ | (1) |
当整个界面上发生黏塑性变形时,扭矩达到其峰值,此时θf与θp相等。
滑动摩擦向黏着状态的转变是金属加工中广泛存在的问题。对于摩擦焊而言,这一转变本质是对产热机制的理解,是建立摩擦焊产热模型的基础。目前多数理论根据材料状态,如温度和应力应变状态,作为转变判据。MEPP考虑到摩擦焊过程的非平衡、非线性和热力耦合复杂性,从两种摩擦方式产热原理的角度通过热力学分析得到形式简明的判据。然而,更准确、有效地描述摩擦焊过程的热力耦合行为理论,还有待继续深入研究。
1.2 摩擦焊过程的产热模型根据摩擦机制,摩擦焊过程的产热模型主要分为3种类型:简化为滑动摩擦产热的经典模型、考虑塑性变形的变形产热模型、考虑黏塑性金属塑性流动行为的热力耦合模型。
滑动摩擦产热模型仅考虑产热率与速度、摩擦系数、轴向压力有关。Rykalin等[21]和Vill[22]使用恒摩擦系数假设,将压力与界面摩擦建立关系,得到界面热流密度与半径的平方成正比,
| $ \frac{\mathrm{d} q_{\mathrm{s}}}{\mathrm{~d} r}=2 {\rm{\mathsf{π}}} \omega f p r^{2} . $ | (2) |
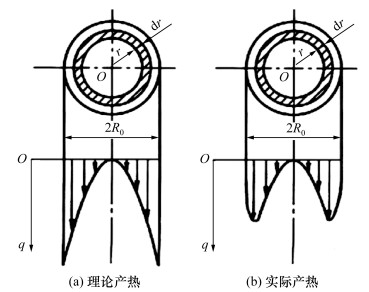
式中:qs为界面产热率,r为所在位置半径,ω为角速度,p为轴向压力,f为摩擦系数。式(2)揭示了旋转摩擦焊在径向上产热的不均匀性。然而,在实际焊接过程中,施加的摩擦压力并不均匀地分布在界面上。由于RFW焊接界面上相对运动速度沿径向增加,焊件边缘热输入较大,温度较高使得材料软化,相对其他位置塑性更高,因此局部压力在边缘较低,中心较高,而相对速度在中心趋向于零,于是最大产热量分布在(1/2)R0~(2/3)R0之间[22-23],如图 4所示。这种压力的不均匀分布使得界面热流密度分布反而更加均匀。
Crossland[24]考虑界面压力的不均匀分布,认为界面压力与半径呈双曲线关系,使用压力分布函数pr替换式(2)中的压力值,得到
| $ p_{\mathrm{r}}=\frac{R_{0}}{2 r} p . $ | (3) |
在实际应用滑动摩擦产热模型时,通常将各摩擦阶段不同的产热情况概括为摩擦系数的变化。尽管在一般摩擦问题中普遍使用的Coulomb摩擦定律认为,摩擦力与法向载荷成正比,摩擦系数与接触面积无关、与滑动速度无关,但研究 [1, 25-26]表明,法向压力、滑动速度和温度等摩擦测量条件会影响摩擦系数的具体值。Kragelskij和Vinogradova提出了一个确定摩擦系数的一般方程[1],
| $ f=(A+B v) \exp (-C v)+D . $ | (4) |
他们认为在不同的法向压力下,摩擦系数随相对运动速度v变化。随着速度的增加,摩擦系数呈现的变化规律与压力相关,具体取决于方程(4)中的4个系数(A、B、C和D)及法向压力的大小,而这些系数的值取决于材料的性质。方程(4)的主要缺点是仅仅确定了摩擦系数与滑动速度的函数关系,没有考虑其他参数,如压力和温度。
Balasubramanian等[25]根据实验结果,通过回归分析得到了与温度、压力和速度相关的摩擦系数模型,
| $ f=a_{0} T^{a_{1}} p^{a_{2}} v^{a_{3}} . $ | (5) |
式中:a0是常数系数,a1、a2、a3是可以由标准多元线性回归方法确定的指数,T是界面温度。
由于相对速度随半径呈线性变化,Balasubra- manian等在计算中使用了加权平均速度,其值等于2/3的工件外缘线速度。
结合以上两种表达形式,Zhang等[26]针对高温合金提出了与轴向压力p、温度T和相对运动速度v相关的摩擦系数模型,
| $ f=f_{0} p^{a} T^{b} \exp (c v) . $ | (6) |
式中:f0、a、b、c是通过实验获得的常数。
摩擦系数受到很多因素的影响,包括表面粗糙度、温度、相对运动速度、施加压力和材料特性等。因此,对于不同的材料和焊接工艺参数组合,摩擦系数存在不同的变化规律,难以找到普适的模型进行准确描述。
滑动摩擦模型本质上只能在摩擦初始阶段较为准确地描述产热过程,而随着热量积累,材料发生塑性变形,界面剪切力不再直接与法向压力成正比,无法使用基于Coulomb摩擦的模型进行准确计算。进入黏着摩擦阶段后,摩擦剪切力与屈服应力相关。
Maalekian等[16]根据滑动-黏着机制,引入了界面黏着分数δ解决产热过程中滑动摩擦向黏着摩擦转变的过程,界面热流密度为
| $ q=(1-\delta) f p v+\delta \tau_{\mathrm{y}} v . $ | (7) |
式中:δ在[0, 1]中取值,取0时全部为滑动摩擦,取1时全部为黏着摩擦。
Li等[27]考虑RFW过程中的同轴性偏差,引入压力分布与同轴性偏差相关系数ξ,给出界面热流密度为
| $ q=\frac{\xi \tau_{\mathrm{f}} \omega r^{2}}{R_{0}}+(1-\xi) \tau_{\mathrm{f}} \omega R_{0} . $ | (8) |
结合滑动摩擦模型和黏着摩擦模型,以分段函数的形式建立了摩擦体系瞬态演化分析模型,将摩擦应力定义为
| $ \tau_{\mathrm{f}}= \begin{cases}f p \text { (Coulomb 摩擦状态) }, & f p<m \frac{\sigma_{\mathrm{y}}}{\sqrt{3}} ; \\ m \frac{\sigma_{\mathrm{y}}}{\sqrt{3}} \text { (黏着摩擦状态) }, & f p \geqslant m \frac{\sigma_{\mathrm{y}}}{\sqrt{3}} .\end{cases} $ | (9) |
式中:m是黏着摩擦系数,σy是材料屈服强度。由此,界面摩擦热流密度表示为
| $ q=\eta \tau_{\mathrm{f}} \omega r. $ | (10) |
式中η是摩擦的热机械效率。Tang等[28]的模型准确地预测了黏着摩擦区从工件外围形成时Coulomb摩擦区的收缩情况。
Doege等[29]撰写的《金属成形手册》中采用了相似的思路,但为了实现滑动摩擦至黏着摩擦的平滑过渡,使用双曲正切函数结合了两种摩擦过程的表达式,
| $ \tau_{\mathrm{f}}=\tau_{\mathrm{y}}\left[\tanh \left(\frac{f p}{\tau_{\mathrm{y}}}\right)^{k}\right]^{\frac{1}{k}} . $ | (11) |
这类模型通过使用剪切屈服应力τy将黏着和材料屈服建立联系,得到了黏着机制中塑性变形产热的定量表述。
随着摩擦焊过程的持续进行,温度进一步升高,焊接界面被黏塑性金属层覆盖,此时黏塑性金属作为产热的主要来源,通过内部的塑性流动将机械能转化为热量。黏塑性金属层作为与应变率相关的内热源,既产生热量也参与热传导过程。滑动摩擦模型和塑性变形模型能够通过使用名义摩擦系数和剪切屈服应力的方式,在总产热量上考虑塑性变形产热,但本质仍是针对面热源,与实际边界条件不一致,无法获得准确的产热过程和温度场。对于黏塑性阶段,金属层内部的单位体积产热率或机械能的耗散率可以表述为应力与应变率的乘积[11, 30],
| $ q=\eta \sigma \dot{\varepsilon} $ | (12) |
式中:
综上所述,摩擦焊产热过程受到界面应力场的影响,而温度场同样影响材料的塑性状态,整个焊接过程中热和力相互作用、密切耦合。
2 旋转摩擦焊的解析计算方法解析计算方法能够直观描述焊接过程中的本质规律和各类边界条件,计算效率高,能够得到温度和应力场随各工艺参数变化的定量规律。但由于解析求解方法通常只能应用于线性、稳态和平衡问题,目前摩擦焊的解析求解主要采用恒系数假设简化,或仅针对黏塑性状态的稳态阶段进行热力耦合计算。
Healy等[11]针对薄壁管的RFW,从动力学角度提出了一种用于温度场求解的黏塑性模型。假设界面两侧各有一层厚度为H的黏塑性材料并符合Bingham塑性流变模型,在此基础上进行温度依赖性修正,得到黏塑性层内的应力平衡方程,
| $ \mu(\dot{\varepsilon})\left(\frac{\mathrm{d} v}{\mathrm{~d} x}\right)+G(T)=\tau_{\mathrm{f}} . $ | (13) |
式中:
同时,考虑能量守恒方程,
| $ \kappa \nabla^{2} T=\boldsymbol{V} \cdot \nabla T-\frac{q}{\rho C_{p}} . $ | (14) |
式中:
联合式(13)和(14),并结合相关边界条件,求解得到界面处温度为
| $ T=\left(T_{\mathrm{m}}-\frac{\tau_{\mathrm{f}}}{\epsilon}\right)\left(1+\frac{2}{{\rm{\mathsf{π}}}} \frac{w^{\infty} H}{\kappa}\right) . $ | (15) |
式中:
该模型充分考虑了材料的黏塑性状态,但需要实验测量获得扭矩及黏塑性层厚度,并通过扭矩计算出所需的剪切力,因此是非完全的解析模型。
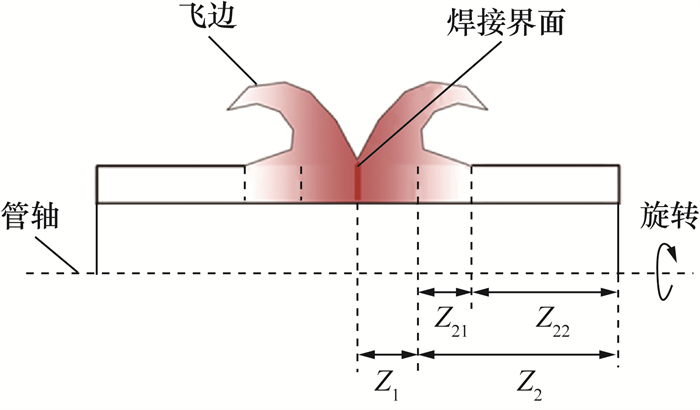
Xiong等[31]针对同种薄壁管状金属材料的连续驱动摩擦焊的稳态阶段建立了解析模型,假设忽略径向温度、相对速度、应力应变的变化,压力和转速保持不变,扭矩和轴向缩短率保持不变。如图 5所示,该模型将准稳态阶段的焊件分为3个主要区域:
塑性区、部分变形区、未变形区。塑性区发生黏塑性流动,产生显著的DRX,即焊核区;部分变形区仅发生明显变形但不流动,尽管这一区域发生了塑性变形,但应变率较小,产热量可以忽略。这一模型将准稳态阶段的焊接过程抽象为各个场由焊接界面向轴向末端平移的一维问题。塑性区单位体积产热率使用等效应力σe和等效应变率
| $ q \approx \psi \frac{1.27}{\sqrt{3}}\left(\frac{L-x}{n \alpha H}\right) \frac{v}{H} \exp \left(-\frac{x}{H}\right) . $ | (16) |
式中:ψ是x方向传热量占塑性区域总产热量的百分比,L是焊接界面与夹具夹持位置的距离,n和α是Sheppard-Wright本构模型中的材料参数。
进一步地,根据Fourier热传导方程(式(17)),可以求解得到黏塑性区的温度分布解析解。
| $ \kappa \frac{\mathrm{d}^{2} T}{\mathrm{~d} x^{2}}+\frac{q}{\rho C_{p}}+V \frac{\mathrm{~d} T}{\mathrm{~d} x}=0 . $ | (17) |
李鹏等[32]则分析了薄壁管旋转摩擦焊初始滑动摩擦阶段的产热和温度场,将模型简化为一维,忽略了对流和辐射换热以及热物性参数随温度的变化。他们提出了一种基于滑动-黏着摩擦过渡准则的解析产热模型,认为当摩擦界面等效应力超过屈服应力时进入黏着摩擦状态,通过建立材料屈服强度与温度相关的表达式,得到了摩擦机制转变温度,作为初始滑动摩擦阶段的最高温度,即模型的右极限。他们使用了反双曲正弦材料模型,以摩擦扭矩做功的方式计算得到界面产热率,结合热传导方程,得到了初始摩擦阶段温度场的数学表达式。
尽管不同研究使用的简化方式和模型各异,但总体而言,RFW的解析计算主要通过4组方程进行:1) 材料流动方程或应力平衡方程,建立宏观位移、速度与应力及应变率的关系;2) 材料本构方程,建立应变率与应力和温度的关系;3) 产热方程,建立速度或应力应变率与热流密度的关系;4) 能量守恒方程或热传导方程,建立热流密度与温度的关系。然后,再结合各类边界条件,求解得到应力场和温度场。目前,在研究中常使用的材料模型如表 1所示[8, 33-34]。
| 模型类型 | 表达式 | 公式编号 |
| 刚塑性体 | (18) | |
| Bingham刚黏塑性流体 | (19) | |
| Newton黏塑性体 | (20) | |
| 超塑性体 | (21) | |
| Maxwell模型 | (22) | |
| Sellars-Tegart 塑性流变 |
(23) | |
| Sheppard-Wright 塑性流变 |
(24) |
表 1中:ν为流变系数;μ为黏滞系数;m为应变率敏感性指数;K为常数;E和φ分别是Maxwell模型中的弹性模量和黏度;A是结构因子;Q为热激活能;R为气体常数;Z为Zener-Hollonmon参数,描述变形温度和变形速率对变形的影响,
| $ Z=\dot{\varepsilon} \exp \left(\frac{Q}{R T}\right) . $ | (25) |
式(23)中的F(σ)是应力的函数,根据不同的应力范围,有3种表达形式[35-36]:
| $ F(\sigma)=\sigma^{n}(\text { 低应力 } \alpha \sigma<0.8), $ | (26) |
| $ F(\sigma)=\exp (\alpha n \sigma)(\text { 高应力 } \alpha \sigma>1.2) \text {, } $ | (27) |
| $ F(\sigma)=[\sinh (\alpha \sigma)]^n \text { (所有应力). } $ | (28) |
实际上,将式(28)代入式(23)中,即能得到式(24)。式(26)—(28)中的模型虽然形式不同,但除刚塑体外都能够反映焊核区金属塑性流动应力与应变率相关的黏性流动特征,Sellars-Tegart(式(23)) 和Sheppard-Wright(式(24))则进一步引入了温度对塑性变形过程的影响。
RFW的热力耦合模型已取得了大量研究成果,为焊接产热机制分析提供了可靠参考。但是,由于摩擦焊全过程中温度变化范围较大,材料状态在不同焊接阶段中差异较大,目前仍缺乏对于焊接全过程的解析。摩擦焊过程本质是物理非线性、几何非线性、非平衡的,同时涉及材料流动和飞边挤出,其复杂性使得目前能够获得解析解的热力耦合模型均大幅简化为一维模型。对于RFW而言,这类模型仅适用于薄壁管的焊接,而无法准确描述棒状等大截面工件径向不均匀产热、受力及材料流动情况。
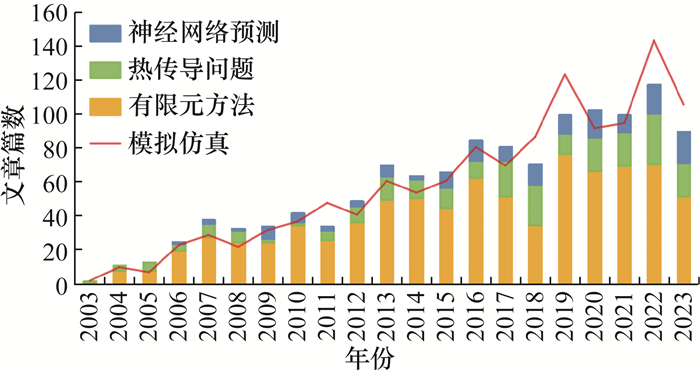
3 旋转摩擦焊的数值计算方法由于摩擦焊过程中涉及复杂的热效应和机械效应耦合,很难仅通过实验来研究接头的温度演化和塑性变形。解析方法在处理瞬态热传导问题时,通常假设材料热物理性质恒定,仅适用于温度变化较小或在焊接过程中热物理性质变化较小的情况;当问题涉及温度相关的热物理性质、相变、变形、辐射和对流换热时,难以通过数理方程获得解析解。因此,具有更好泛用性的数值解法是目前摩擦焊研究的主要方法[37]。图 6为根据Web of Science数据库统计的近年摩擦焊数值仿真研究情况。可见,随着计算机数值计算和仿真技术的迅速发展,产生了大量摩擦焊模拟仿真方法。
|
| 图 6 Web of Science数据库中近20年内摩擦焊仿真研究情况 |
3.1 旋转摩擦焊的热传导数值模型
在摩擦焊研究中,焊接过程中的温度变化对接头成形及组织性能有直接影响,而焊接界面处于高速运动状态,并存在显著变形,难以通过实验方法直接获得界面内部的温度,数值模型成为进行温度场研究的重要手段。RFW的基本数值计算主要从热输入和热传导的角度出发,采用有限差分法(finite difference method, FDM)或有限体积法(finite volume method, FVM)等数值求解方法,对焊接过程中的瞬态温度场进行数值求解。FDM采用固定网格,能够实现热传导偏微分方程的快速求解;FVM则直接基于能量守恒,能够考虑空气对流等因素对热传导过程进行求解。结合解析方法的分析,相关数值模型主要可分为4类[38]:恒摩擦系数模型、滑动-黏着摩擦模型、实验功耗模型和逆热传导模型。恒摩擦系数模型已被证明可靠性较低;滑动-黏着摩擦模型依赖于摩擦系数及材料热物性参数的准确性,由此演变出了多种相关参数计算方法或模型;实验功耗模型和逆热传导模型为计算焊接界面热通量提供了简单有效的方法,利用实验测量的扭矩、功率或焊接界面附近的温度求解热通量,但二者均是通过已有实验过程测量数据进行回顾性分析的方法,无法进行前向预测分析。
1962年,Cheng[39]首先应用数值方法进行摩擦焊分析。他认为焊接界面处温度达到了熔点,并应用一系列简化假设,基于热传导理论,使用一维FDM模型计算了AISI 4149合金钢摩擦焊过程中的温度分布。他通过实验测得的扭矩计算得到随时间变化的摩擦热输入,作为模型中的热源。尽管假设工件侧面绝热,但在焊接初期,计算得到的温度与测量得到的温度吻合较好,而在较长的摩擦时间中计算得到的温度低于实验值。
Wang和Nagappan[40]研究了AISI 1020钢棒惯性摩擦焊的瞬态温度分布,根据Vill[41]提出的摩擦系数与线速度平方成反比的关系式计算得到热输入,通过二维FDM模型求解得到温度分布。他们验证了惯性摩擦焊中界面温度没有到达金属熔点,与连续驱动摩擦焊的峰值温度相当。
Bouarroudj等[42]利用热传导的FVM模型,得到了棒状工件RFW的最佳焊接时间,考虑了随温度变化的材料比热容、导热系数、空气导热系数以及与空气的自然对流。他们使用交替方向隐式迭代法(alternating direction implicit, ADI)对偏微分方程进行离散,其中热源使用了式(2)的滑动摩擦模型,摩擦系数采用了Słu Az·G5 alec[43]实验测得的随温度升高先迅速增加、在高温时急剧下降的规律,并通过四阶Lagrange插值拟合。他们最终得到了一个三对角线性方程组,并使用Thomas算法和Gauss-Seidel迭代法求解。比较实验和仿真结果,Bouarroudj提出了一个确定最佳摩擦时间的相关关系式,
| $ t=0.0077634 \rho_{\text {mean }} C_{p, \text { mean }}\left(a \lambda_{\text {mean }}^{b}\right) d^{1.79}\left(N p f_{\text {mean }}\right)^{-0.97}. $ | (29) |
其中:
Wang等[38]为建立304不锈钢连续驱动摩擦焊的热流模型,采用实验功耗方法,即通过实验测量的设备功率计算焊接界面热流,得到
| $ q=\frac{\varOmega}{s} . $ | (30) |
式中:
| $ \begin{gather*} q=Q_{\mathrm{c}}+\frac{\left(Q_{0}-Q_{\mathrm{c}}\right) t_{1}}{4\left(t-t_{0}\right)^{2}+t_{1}^{2}}- \\ \left(Q_{\mathrm{c}}+\frac{\left(Q_{0}-Q_{\mathrm{c}}\right) t_{1}}{4 t_{0}^{2}+t_{1}^{2}}\right)\left(\frac{\mathrm{e}^{-3 t}}{1+3 t}\right) . \end{gather*} $ | (31) |
式中:t0、t1、Q0、Qc均是通过回归拟合得到的与摩擦压力和转速线性相关的特征值。他们通过实验验证了该模型的准确性。
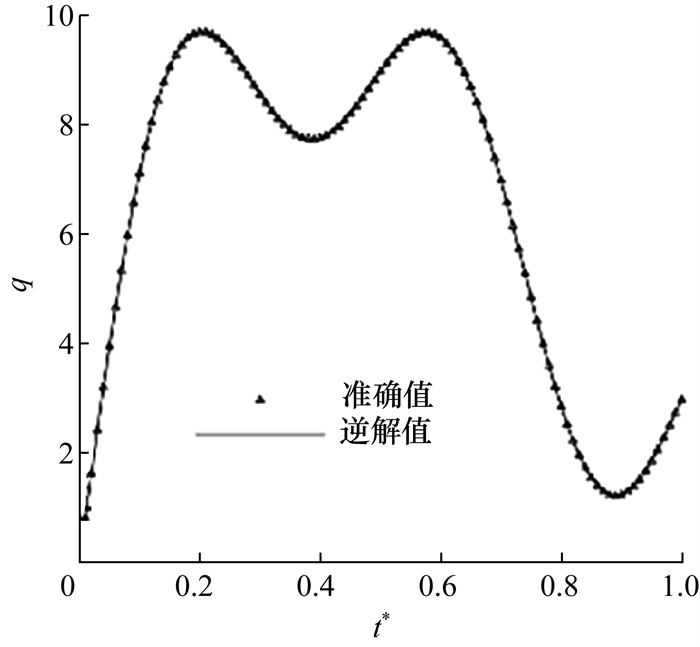
Chen等[44]通过共轭梯度法(conjugate gradient method, CGM) 和偏差原理求解得到圆棒旋转摩擦焊过程中焊接界面的热输入,从而确定棒材中的热量分布。构造函数为
| $ \begin{gather*} J\left[q\left(t^{*}\right)\right]=\int_{t^{*}=0}^{t_{\mathrm{f}}^{*}}\left[\phi\left(1, -z_{\text {mea }}^{*}, t^{*}\right)-\right. \\ \left.\psi\left(1, -z_{\text {mea }}^{*}, t^{*}\right)\right]^{2} \mathrm{~d} t^{*} . \end{gather*} $ | (32) |
式中:
IHCP采用物体内部或表面的温度信息来反求物体的某些未知信息,如热物性参数、边界条件以及热源项等。事实上,不仅是摩擦焊,IHCP在化工、材料、航天、无损探伤、动力工程、冶金工程和生物工程等领域都有着广泛的应用。随着计算科学的进步,IHCP也逐渐发展出了多种求解方法[45],如熔化焊研究中[46],将热传导逆问题求解与有限元、微观组织模拟或神经网络等仿真预测方法结合,利用焊接过程中的测量值,更准确地获取材料参数[47]。这些方法为未来摩擦焊的产热问题研究提供了可借鉴的思路。
3.2 摩擦焊有限元模型近年来,有限元法(finite element method, FEM)越来越多地应用于摩擦焊过程仿真分析。由于FEM强大的计算能力能够充分地考虑焊接过程中复杂的结构变形和非线性材料模型,并进行由二维到三维的热力耦合分析,获得包括温度、应力应变、轴向缩短量和飞边形貌在内的多种焊接信息,FEM为摩擦焊接头成形研究提供了有力支撑[48-50]。1990年,Słu Az·G5 alec[43]首先将FEM应用于摩擦焊的热力耦合模型计算,采用变热物性参数(导热系数、比热容和屈服应力)以及与温度相关的摩擦系数,基于热塑性有限元计算的增量理论和二维轴对称模型,成功预测了低碳钢的温度场和应力场。该研究使用热源模型,
| $ q_{\mathrm{s}}=\int_{s} \sigma \mu \omega r \mathrm{~d} s , $ | (33) |
以及固体在热载荷和机械载荷共同作用下的本构方程,
| $ \dot{\sigma}_{i j}=c_{i j k l}^{e p} \dot{\varepsilon}_{k l}+\gamma_{i j} \dot{T}, $ | (34) |
忽略辐射散热与对流散热,根据能量守恒定律,推导出模型:
| $ \begin{gather*} \int_{\varOmega}\left(c_{i j k l}^{e p} \dot{\varepsilon}_{k l}\right) \dot{\varepsilon}_{k l} \mathrm{~d} \varOmega+\int_{\varOmega} \gamma_{i j} \dot{T} \dot{\varepsilon}_{i j} \mathrm{~d} \varOmega= \\ \int_{\varOmega} \dot{f}_{i}^{\mathrm{v}} \mathcal{v}_{i} \mathrm{~d} \varOmega+\int_{\partial \varOmega} \dot{f}_{i}^{\mathrm{s}} \mathcal{v}_{i} \mathrm{~d}(\partial \varOmega) . \end{gather*} $ | (35) |
| $ \begin{gather*} \int_{\varOmega}\left(\rho C_{p}+\gamma\right) T \dot{T} \mathrm{~d} \varOmega-\int_{\varOmega} T \bar{\beta}_{i j} \dot{\varepsilon}_{i j} \mathrm{~d} \varOmega- \\ \int_{\varOmega} D T \mathrm{~d} \varOmega-\int_{\varOmega} Q_{i} T \mathrm{~d} \varOmega= \\ \int_{\varOmega} \lambda_{i j} T{ }_{\cdot i} T \cdot{ }_{\cdot j} \mathrm{~d} \varOmega+\int_{\partial \varOmega} T q_{i} n_{i} \mathrm{~d}(\partial \varOmega) . \end{gather*} $ | (36) |
式中:
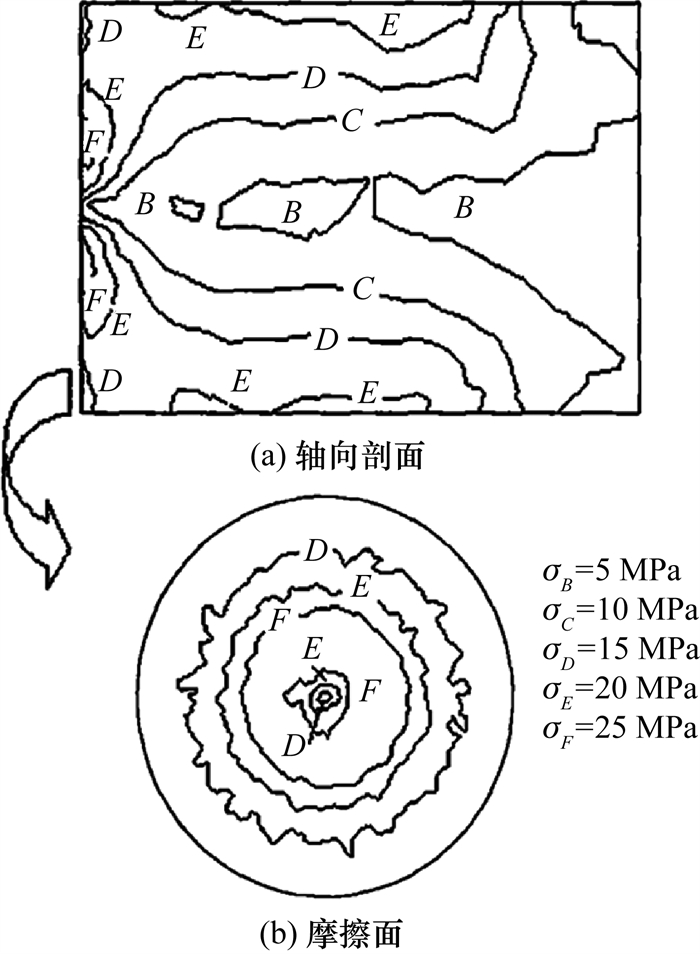
张全忠等[51]对比了连续驱动摩擦焊过程的二维和三维FEM模型,发现二者对于焊接过程温度场的模拟结果均与实验结果吻合较好。三维模型和二维模型的差别在于三维模型考虑了摩擦面上的环向摩擦力,即环向剪应力。焊接过程中,在摩擦面靠近旋转轴中心的圆环区域内,环向剪应力较大,越远离摩擦面的外侧,环向剪应力越低,如图 8所示。由于计算了环向摩擦力,三维模型得到的等效应力大于二维轴对称模型的计算结果,并且计算得到的飞边形状和轴向缩短量更接近实验结果。该研究证明了旋转摩擦焊过程中,环向剪应力对接头成形起到了不可忽视的作用。
进一步地,张全忠等[26]将扭转摩擦引入产热和变形的计算中,使用DEFORM软件建立了三维刚黏塑性FEM模型,将工件视为刚黏塑性不可压缩材料的可变形体,在变形区有
| $ \dot{\varepsilon}_{i j}=\frac{3 \dot{\bar{\varepsilon}}}{2 \bar{\sigma}} \sigma_{i j}^{\prime} . $ | (37) |
式中:
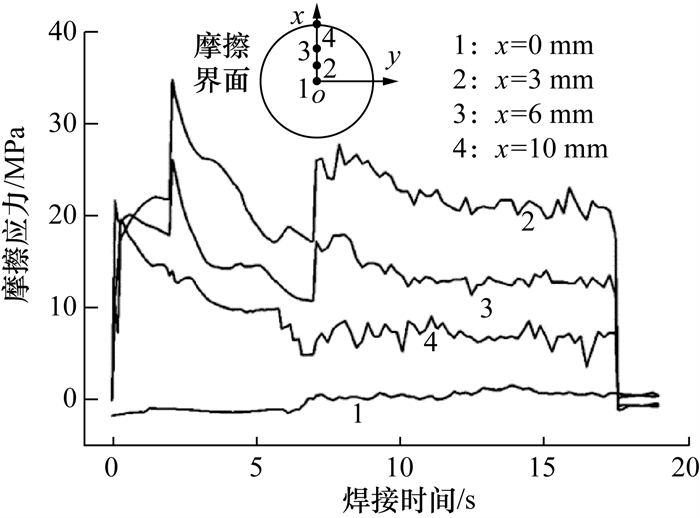
张全忠等[26]在模型中还使用了二级摩擦应力的计算方法:在低温时,应用Coulomb摩擦;温度较高时,采用黏着摩擦;并假设摩擦应力与材料的屈服强度成正比。图 9中展示了焊接过程中摩擦界面上不同径向位置摩擦应力的变化。可以发现,黏着摩擦阶段应力趋于稳定,除中心外,内部摩擦应力高于边缘。他们认为是由于剪切摩擦应力与屈服强度成正比,而内部温度较低,应变率较高,使得摩擦应力值较高。该模型成功预测了接头的温度场变化、形变率和飞边形状。
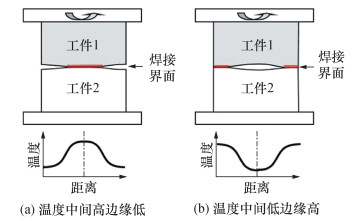
Lei等[52]在DEFORM中采用完全耦合FEM分析,将两个工件视为两个接触实体,提出了一种基于等效热膨胀(thermal expansion, TE)系数的方法,以研究低压力旋转摩擦焊的动态接触行为。他们使用式(37)的材料模型作为塑性形变率表达式,同时考虑弹性应变率和热膨胀应变率,总应变率为三者之和。在不同界面温度分布下,工件可能会有不同的接触行为,如图 10所示。他们通过尝试不同的TE系数设置方式,发现相比设为0或使用材料实际的TE系数αe,使用式(38)所示的等效TE系数αe,E能够获得更准确的结果。
| $ \alpha_{\mathrm{e}, \mathrm{E}}=\alpha_{\mathrm{e}}-\alpha_{\mathrm{w}}^{\prime} . $ | (38) |
等效TE系数考虑了摩擦界面磨损造成的材料损失α'w远低于材料本身的实际热膨胀系数。他们通过实验得到等效TE系数与温度相关的经验公式,代入模型计算发现接触区域在摩擦阶段会持续膨胀。
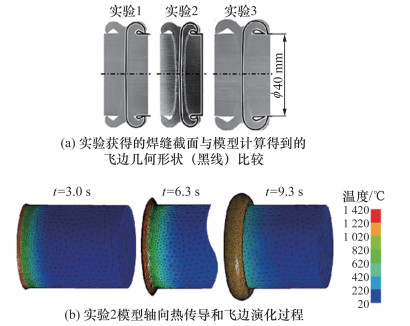
Kessler等[53]利用黏弹性Maxwell模型在LS-Dyna软件中建立了旋转摩擦焊的三维FEM热力耦合模型。摩擦界面产热通过式(11)的模型进行计算,仿真结果表明焊接过程中界面温度未超过熔点,模型能够成功预测飞边形状演化和轴向缩短量,如图 11所示。
除了研究模型及焊接机理,FEM也为各类材料应用RFW的工艺参数探索提供了便利[54]。Mattie等[55]研究了TP347HFG奥氏体不锈钢与HiPerFer铁素体不锈钢的异种材料旋转摩擦焊。他们利用ANSYS软件开发了一个三维FEM模型,分析了工艺参数与焊接结果间的关联性。结果表明,摩擦压力和摩擦时间对界面温度的影响较大,而顶锻压力和摩擦时间会直接影响等效应力,摩擦速度和顶锻压力则对总变形量的影响较大。张昌青等[56]使用ABAQUS软件对1060工业纯铝棒和具有锥形端面的Q235低碳钢的连续驱动摩擦焊进行了FEM分析, 采用耦合的Euler-Lagrange (coupled Euler-Lagrange, CEL) 方法和Johnson-Cook材料模型,建立了焊接过程的三维热力耦合模型,分析了接头成形、温度场分布和塑性金属的形成随(锥形)端面锥度的大小变化的规律。
目前,RFW的有限元模型大多基于Lagrange网格划分进行计算,通常使用网格重划分技术以解决摩擦焊过程中大变形引起的网格畸变。在流体仿真和大变形仿真中还常使用CEL模型,但由于CEL方法计算成本较高,目前多用于材料流动更加剧烈的搅拌摩擦焊研究[57]。此外,还有折衷的任意Lagrange-Euler(arbitrary Lagrange-Euler, ALE)方法,可提供对大变形或材料损失时单元形状扭曲的控制,提高模型计算的鲁棒性,比CEL方法操作简单、计算量小。与ALE建模技术相比,CEL建模技术更准确、易于使用,计算效率更高[58]。
摩擦焊的FEM模型能够很好地处理非线性问题,从而允许根据不同的材料特性和焊接条件,灵活地设置不同的材料流动模型、热源模型和边界条件。尽管FEM能够高效便捷地实现各类模型求解,对于摩擦焊过程,FEM仍面临许多技术难点[59]:
1) 热力耦合导致计算过程复杂。FEM包括热分析和力分析。对于完全(直接)耦合方法,在每个时间步中并行计算。在力分析中,根据塑性变形的计算会影响温度场分布;从力分析传递数据后,通过热分析更新温度,而后继续计算应变和应力。在分析的每一步都以此顺序进行,计算量大、模型收敛难度高。对于顺序(间接)耦合方法,则通常是先进行全摩擦过程的热分析,再将计算得到的温度场变化结果传递至力分析进行计算。顺序耦合能够大幅提高计算速度,但需要对热分析和力分析进行解耦,准确性较差。
2) 材料非线性。材料的性质直接影响仿真预测的准确性[60],针对特定材料需要采取合适的本构模型,并且获得与温度相关的准确热物性参数及材料流动数据。
3) 复杂的边界条件。热边界条件包括界面摩擦产热的热通量以及从摩擦界面向工件内部热传导过程中的对流换热和辐射热损失。目前对流换热系数通常以自然对流估计,但实际焊接过程存在工件高速运动,对流换热系数难以准确测算。此外,力边界条件同样复杂,在实际焊接中,界面实际接触情况和摩擦系数都随时间和温度不断变化,需要对这一过程进行合理考虑。
3.3 微观组织预测的数值模型在面向应力场、温度场和位移场仿真的常规FEM基础上,为了能够更好地了解摩擦焊工艺过程对接头成形质量的影响,产生了一类考虑微观组织的数值模型。这类模型进一步联合其他计算方法,考虑实际焊接过程中组织转变对仿真过程的影响,借助动力学模型或多尺度仿真手段,明晰接头组织转变过程和组织分布情况。
Heppner等[61]针对铝合金与钢的异种材料旋转摩擦焊过程,建立了一个表征钢-铝界面间键形成及键合强度的模型。该模型使用定量描述固态焊接过程中键形成的指标β,建立与键合强度B的函数关系,
| $ B=\mathcal{F}(\beta) . $ | (39) |
指标
| $ \mathcal{F}(\bar{\beta})=B^{*} \exp (-a \exp (-b \bar{\beta})) . $ | (40) |
借助FEM仿真获得的温度场和应力场,以及实验测试数据,采用最小二乘法可获得函数中的各项参数(a和b),最终实现了根据焊接工艺参数对键合强度进行预测。
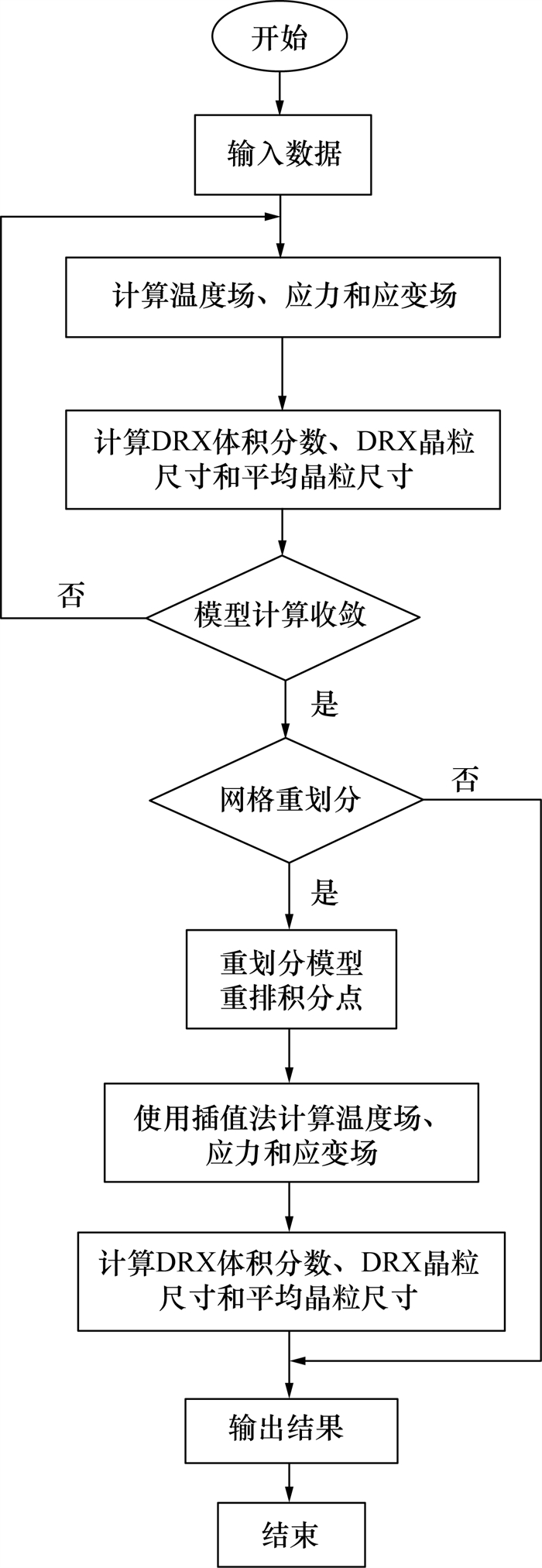
Nie等[62]为了研究FGH96环形工件惯性摩擦焊过程的微观组织演化,建立了FGH96高温合金的DRX动力学模型。他们使用MSC.Marc软件,借助子程序二次开发技术,将DRX动力学模型嵌入二维轴对称热力耦合FEM模型中,得到了惯性摩擦焊过程中DRX体积分数和平均晶粒尺寸的分布。DRX子程序的流程图如图 12所示。在每个时间增量下,首先利用热力耦合FEM模型得到FGH96焊接件的温度场和应力应变场,然后传递给子程序,子程序再根据宏观场变量的模拟结果来预测DRX的行为。
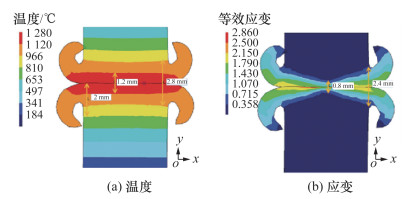
随着近年来多尺度多物理场数值模拟技术的发展,摩擦焊过程中的微观组织演变有了更加直观的仿真手段,常用的三维微观组织演变的模拟方法主要有 [63]:Monte Carlo(MC)法、元胞自动机(cellular automata, CA)法和相场法(phase field method, PFM)。前二者均为随机性方法,能够考虑组织演变过程中的各种随机现象。Reyes等[64]在DEFORM软件中采用CA法研究铬镍铁合金718圆柱形构件的RFW接头,预测焊缝DRX过程和晶粒尺寸。CA法基于Laasraoui-Jonas模型,从微观结构、温度和应力应变等方面解释了复杂的晶粒转变,首先通过FEM模型获得接头的温度场和应力应变场,焊缝中心区达到最高温度1 200℃,最大等效应变0.9,如图 13所示。
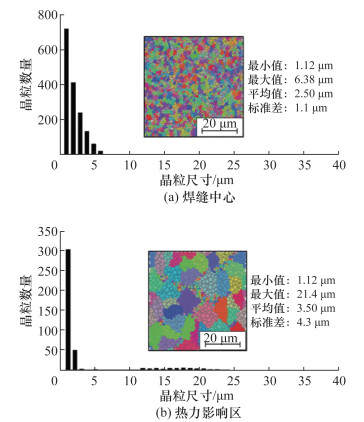
再结合CA法计算微观组织信息,得到如图 14所示的一系列微观组织仿真结果。在焊缝中心区有非常细的晶粒结构,平均晶粒尺寸2.5 μm,远小于母材的80 μm;在热力影响区,平均晶粒尺寸3.5 μm,其中存在部分再结晶晶粒。计算获得的平均粒径与实验值相当(两区域分别为2.0 μm和4.5 μm)。晶粒分析表明,温度和应变是影响精细微观结构的最大因素。
摩擦焊接头涉及复杂的再结晶或相变过程,焊缝组织对性能有直接影响。借助多尺度的仿真方法,能够更好地解释焊接工艺参数对焊缝组织的作用过程,也能够进一步优化仿真模型以获得更准确的结果,为工程应用中的焊接工艺参数选择提供指导。
3.4 其他分析手段在旋转摩擦焊仿真中的应用尽管实验和FEM能够对摩擦焊过程进行充分研究,但仍需要花费大量成本和时间,且无法对连续变化的工艺参数进行实验,在获取所需的接头质量、寻找优选的工艺参数方面存在大量限制。因此,在实验或FEM计算的基础上,为便于在工程应用中对工艺参数选择优化进行指导,以神经网络为主的模型被用于摩擦焊的接头成形预测。
Maalekian等[65]建立了一种神经网络模型,将飞边尺寸方面的焊接完整性与摩擦焊参数联系了起来。Liu等[66]研究了GH4169高温合金惯性摩擦焊接头的轴向缩短量预测问题,基于FEM仿真模型建立了径向基函数(radial basis function, RBF) 神经网络。他们将RBF神经网络预测的轴向缩短量与FEM仿真结果进行验证比较,误差小于8.16%。此外,这一神经网络模型还被用来研究初始转速和轴向压力对轴向缩短量和飞轮能量转化的影响,以及线性摩擦焊和连续驱动摩擦焊,实验结果均与仿真结果有较好的一致性,证明了RBF神经网络在摩擦焊接头预测中具有良好的泛化性能。
此外,神经网络还被大量用于焊接接头力学性能的预测。Palanivel等[67]研究了钛合金旋转摩擦焊工艺参数与接头极限抗拉强度(ultimate tensile strength, UTS)之间的关系。他们使用实验数据作为训练集,分别采用了响应面法(response surface method, RSM)和人工神经网络(artificial neural network, ANN)对UTS进行预测。结果表明,RSM和ANN都能够有效预测摩擦焊接头UTS,但ANN模型在统计学意义上更准确,是描述和预测摩擦焊接钛合金管UTS的可靠工具。模型计算结果表明,转速和摩擦时间分别是影响接头UTS最重要和最不重要的工艺参数。
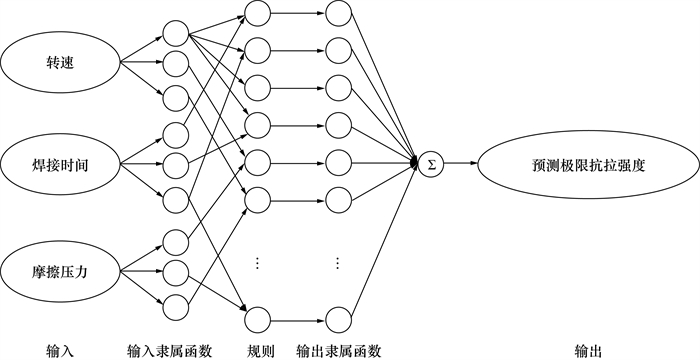
Kunhirunbawon等[68]采用自适应模糊神经网络(adaptive network-based fuzzy inference system, ANFIS),实现了AA6063铝圆棒RFW的参数预测,将转速、焊接时间、摩擦压力等焊接参数输入隶属函数,将焊接接头的UTS作为输出。模型如图 15所示。通过实验数据进行训练和验证,他们发现ANFIS函数模型的结果在预测接头UTS方面非常有效,预测的最大误差百分比仅为0.36%,可以适用于工程应用中自动摩擦焊过程的控制。
目前,卷积神经网络(convolutional neural network, CNN)在摩擦焊预测研究中也逐渐得到了应用。Chiaranai等[69]建立了一种CNN集成的深度学习模型,使用搅拌摩擦焊的焊缝图像,对根据UTS评估的焊缝质量进行分类。Lu等[70]利用多尺度一维CNN,提取搅拌摩擦焊过程中特征点的温度特征和轴向压力的时间序列数据,以预测焊接接头的抗拉强度,实现了在线预测和监测。CNN在搅拌摩擦焊中的研究应用,也为RFW仿真预测的发展提供了可参考的方案。
神经网络对复杂非线性问题高效、准确的预测能力为摩擦焊工艺参数规划和工程应用提供了便捷的解决手段,但其训练集高度依赖大量实验或FEM等数值仿真模型,而训练集的范围通常会影响网络能够有效预测的参数区间。为降低实验和研究成本,仍需要保证仿真模型本身在较大参数范围内的准确性。
4 总结与展望本文总结了近年来RFW热力耦合行为及数值模拟技术的研究进展,包括RFW的摩擦行为理论、产热模型的发展历程以及目前针对焊接过程中温度场、应力场常见的解析和数值计算方法。
1) RFW的提出及研究可以追溯至20世纪50年代,形成了滑动、黏着和滑动-黏着摩擦3种摩擦行为理论,为摩擦焊原理和工艺研究提供了坚实的基础。但是,目前对于焊接过程中的摩擦行为研究仍较为有限,由于摩擦发生在接头内部,难以通过实验手段直接进行验证。尽管围绕滑动-黏着摩擦机制已经提出了大量的理论模型,但对其转变过程及黏着摩擦时的热力耦合行为仍缺乏系统性和统一表述。尤其是摩擦系数和表面压力分布的变化,主要模型是基于经验假设和实验测量获得的,缺乏原理上的普适性。
2) 解析法在摩擦焊产热机制研究中扮演着重要角色,其计算效率高,可直观地揭示摩擦焊过程中的产热、传热规律以及材料流动和变形特征。尽管数值求解技术已经趋于成熟,解析法在RFW机理研究中仍具有不可忽视的价值。但是,解析法存在着求解困难、一维假设和边界条件简化等问题,不同摩擦阶段需要采用不同的数学物理方程,使得解析法难以实现整个焊接过程热力耦合的连贯计算。
3) 数值模拟方法则更加多样,FEM分析作为主流的数值仿真手段,可以应用多种材料流动模型和摩擦模型,从二维到三维地获得焊接过程温度场、应力应变场、焊后残余应力分布、界面接触及接头成形等信息。同时,FEM能够很好地联合其他仿真预测手段,为焊缝组织调控和工艺参数选择优化提供指导。然而,目前摩擦焊过程的仿真准确性高度依赖材料参数的测量,但塑性流动特性和热物性参数的测量实验与实际焊接过程的温度及应力状态有较大差距。并且,焊接过程涉及组织转变,难以获得焊接过程中准确的材料模型,导致仿真模型的预测能力仍较为有限,焊接参数的优化仍主要依赖于试错法。因此,提高仿真建模的效率、升级对接头成形和组织预测的准确性、降低计算成本,是未来RFW数值模拟研究发展的重要方向。
| [1] |
MAALEKIAN M. Friction welding: Critical assessment of literature[J]. Science and Technology of Welding and Joining, 2007, 12(8): 738-759. DOI:10.1179/174329307X249333 |
| [2] |
LI P, JIANG Y, WANG S, et al. Effect of post-weld heat treatment on inhomogeneity of mechanical properties and corrosion behavior of rotary friction welded 2024 aluminum alloy joint[J]. Journal of Manufacturing Processes, 2022, 75: 1012-1022. DOI:10.1016/j.jmapro.2022.01.059 |
| [3] |
AHMED S A, HASANABADI M F, KUMAR A V. Joining of ceramic to metal by friction welding process: A review[J]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2021, 235(7): 1723-1736. DOI:10.1177/14644207211001080 |
| [4] |
NU H T M, LOC N H, MINH L P. Influence of the rotary friction welding parameters on the microhardness and joint strength of Ti6Al4V alloys[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2021, 235(5): 795-805. DOI:10.1177/0954405420972549 |
| [5] |
GHARI H, TAHERIZADEH A, SADEGHIAN B, et al. Metallurgical characteristics of aluminum-steel joints manufactured by rotary friction welding: A review and statistical analysis[J]. Journal of Materials Research and Technology, 2024, 30: 2520-2550. DOI:10.1016/j.jmrt.2024.03.089 |
| [6] |
ARZOUR F Z, AMARA M, SULEIMAN R K, et al. Thermomechanical effect on the properties of stainless steels using rotative friction welding: An experimental study on 304L and 316L grades[J]. The International Journal of Advanced Manufacturing Technology, 2023, 129(9-10): 3849-3861. DOI:10.1007/s00170-023-12522-7 |
| [7] |
BUFFA G, FRATINI L. Strategies for numerical simulation of linear friction welding of metals: A review[J]. Production Engineering, 2017, 11(3): 221-235. DOI:10.1007/s11740-017-0726-7 |
| [8] |
傅莉, 杜随更. 摩擦焊接过程数值模拟技术研究进展[J]. 焊接学报, 2001, 22(5): 87-92. FU L, DU S G. Advance of research on the numerical simulation of friction welding process[J]. Transactions of the China Welding Institution, 2001, 22(5): 87-92. DOI:10.3321/j.issn:0253-360X.2001.05.024 (in Chinese) |
| [9] |
KIMURA M, SEO K, KUSAKA M, et al. Observation of joining phenomena in friction stage and improving friction welding method[J]. JSME International Journal Series A: Solid Mechanics and Material Engineering, 2003, 46(3): 384-390. DOI:10.1299/jsmea.46.384 |
| [10] |
金峰, 熊江涛, 石俊秒, 等. GH4169旋转摩擦焊飞边成形机理研究[J]. 材料导报, 2020, 34(10): 10144-10149. JIN F, XIONG J T, SHI J M, et al. Flash formation mechanism during rotary friction welding of GH4169 superalloy[J]. Materials Reports, 2020, 34(10): 10144-10149. DOI:10.11896/cldb.20030095 (in Chinese) |
| [11] |
HEALY J J, MCMULLAN D J, BAHRANI A S. Analysis of frictional phenomena in friction welding of mild steel[J]. Wear, 1976, 37(2): 265-278. DOI:10.1016/0043-1648(76)90033-8 |
| [12] |
BOWDEN F P, TABOR D. The seizure of metals[J]. Proceedings of the Institution of Mechanical Engineers, 1949, 160(1): 380-383. DOI:10.1243/PIME_PROC_1949_160_036_02 |
| [13] |
HASEGAWA M, IEDA T. Effects of friction welding conditions on initial joining phenomena[J]. Welding International, 1999, 13(9): 701-711. DOI:10.1080/09507119909447434 |
| [14] |
KIMURA M, CHOJI M, KUSAKA M, et al. Effect of friction welding conditions and aging treatment on mechanical properties of A7075-T6 aluminum alloy friction joints[J]. Science and Technology of Welding and Joining, 2005, 10(4): 406-412. DOI:10.1179/174329305X44125 |
| [15] |
MOAL A, MASSONI E. Finite element simulation of the inertia welding of two similar parts[J]. Engineering Computations, 1995, 12(6): 497-512. DOI:10.1108/02644409510799730 |
| [16] |
MAALEKIAN M, KOZESCHNIK E, BRANTNER H P, et al. Comparative analysis of heat generation in friction welding of steel bars[J]. Acta Materialia, 2008, 56(12): 2843-2855. DOI:10.1016/j.actamat.2008.02.016 |
| [17] |
SINGH S K, CHATTOPADHYAY K, PHANIKUMAR G, et al. Experimental and numerical studies on friction welding of thixocast A356 aluminum alloy[J]. Acta Materialia, 2014, 73: 177-185. DOI:10.1016/j.actamat.2014.04.019 |
| [18] |
李京龙, 李洵, 张昊, 等. 摩擦焊产热基础问题探讨[J]. 航空制造技术, 2015, 58(20): 42-46. LI J L, LI X, ZHANG H, et al. Discussion of heat generation in friction welding[J]. Aeronautical Manufacturing Technology, 2015, 58(20): 42-46. (in Chinese) |
| [19] |
WANG G L, LI J L, XIONG J T, et al. Study on the friction interface evolution during rotary friction welding of tube[J]. Journal of Adhesion Science and Technology, 2019, 33(10): 1033-1046. DOI:10.1080/01694243.2019.1575603 |
| [20] |
李鹏. 旋转摩擦焊热源演变及接头成形机制[D]. 西安: 西北工业大学, 2015. LI P. Heat source evolution and joint formation in rotary friction welding process[D]. Xi'an: Northwestern Polytechnical University, 2015. (in Chinese) |
| [21] |
RYKALIN N N, PUGIN A I, VASIL'EVA V A. The heating and cooling of rods butt welded by the friction process[J]. Welding Production, 1959, 6: 42-52. |
| [22] |
VILL V I. Friction welding of metals[M]. New York: American Welding Society, 1962.
|
| [23] |
才荫先, 孙松涛, 朱桂芝, 等. 摩擦焊加热过程中变形层和高温区的扩展过程[J]. 焊接学报, 1984, 5(2): 61-68. CAI Y X, SUN S T, ZHU G Z, et al. The widening process of the deformation layer and the high temperature area in friction welding[J]. Transactions of the China Welding Institution, 1984, 5(2): 61-68. (in Chinese) |
| [24] |
CROSSLAND B. Friction welding[J]. Contemporary Physics, 1971, 12(6): 559-574. DOI:10.1080/00107517108205660 |
| [25] |
BALASUBRAMANIAN V, LI Y L, STOTLER T, et al. A new friction law for the modelling of continuous drive friction welding: Applications to 1045 steel welds[J]. Materials and Manufacturing Processes, 1999, 14(6): 845-860. DOI:10.1080/10426919908914877 |
| [26] |
ZHANG Q Z, ZHANG L W, LIU W W, et al. 3D rigid viscoplastic FE modelling of continuous drive friction welding process[J]. Science and Technology of Welding and Joining, 2006, 11(6): 737-743. DOI:10.1179/174329306X153222 |
| [27] |
LI W Y, WANG F F. Modeling of continuous drive friction welding of mild steel[J]. Materials Science and Engineering: A, 2011, 528(18): 5921-5926. DOI:10.1016/j.msea.2011.04.001 |
| [28] |
TANG T X, SHI Q Y, LEI B W, et al. Transition of interfacial friction regime and its influence on thermal responses in rotary friction welding of SUS304 stainless steel: A fully coupled transient thermomechanical analysis[J]. Journal of Manufacturing Processes, 2022, 82: 403-414. DOI:10.1016/j.jmapro.2022.08.016 |
| [29] |
DOEGE E, BEHRENS B A. Handbuch umformtechnik: Grundlagen, technologien, maschinen[M]. 2nd ed. Berlin: Springer, 2010.
|
| [30] |
MENDEZ P F, TELLO K E, LIENERT T J. Scaling of coupled heat transfer and plastic deformation around the pin in friction stir welding[J]. Acta Materialia, 2010, 58(18): 6012-6026. DOI:10.1016/j.actamat.2010.07.019 |
| [31] |
XIONG J T, LI J L, WEI Y N, et al. An analytical model of steady-state continuous drive friction welding[J]. Acta Materialia, 2013, 61(5): 1662-1675. DOI:10.1016/j.actamat.2012.11.042 |
| [32] |
LI P, LI J L, DONG H G. Analytical description of heat generation and temperature field during the initial stage of rotary friction welding[J]. Journal of Manufacturing Processes, 2017, 25: 181-184. DOI:10.1016/j.jmapro.2016.12.003 |
| [33] |
FRANCIS A, CRAINE R E. On a model for frictioning stage in friction welding of thin tubes[J]. International Journal of Heat and Mass Transfer, 1985, 28(9): 1747-1755. DOI:10.1016/0017-9310(85)90148-6 |
| [34] |
BERGSTRÖM J. Linear viscoelasticity[M]//BERGSTRÖM J. Mechanics of solid polymers. Amsterdam: William Andrew Publishing, 2015: 309-351.
|
| [35] |
刘欣, 李强锋, 汪志刚, 等. 低合金微碳钢的热变形行为及本构方程[J]. 有色金属科学与工程, 2018, 9(4): 53-59. LIU X, LI Q F, WANG Z G, et al. Hot deformation behavior and constitutive equation of low alloy micro-carbon steel[J]. Nonferrous Metals Science and Engineering, 2018, 9(4): 53-59. (in Chinese) |
| [36] |
SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136-1138. DOI:10.1016/0001-6160(66)90207-0 |
| [37] |
AKBARI M, ASADI P, SADOWSKI T. A review on friction stir welding/processing: Numerical modeling[J]. Materials, 2023, 16(17): 5890. DOI:10.3390/ma16175890 |
| [38] |
WANG G L, LI J L, XIONG J T, et al. A heat flux model for rotary friction welding of 304 stainless steel[J]. Materials Research Express, 2019, 6(2): 026558. |
| [39] |
CHENG C J. Transient temperature distribution during friction welding of two similar materials in tubular form[J]. Welding Journal, 1962, 41(12): 542-550. |
| [40] |
WANG K K, NAGAPPAN P. Transient temperature distribution in inertia welding of steels[J]. Welding Journal, 1970, 49(9): 419-426. |
| [41] |
VILL V I. Energy distribution in the friction welding of steel bars[J]. Welding Production, 1959, 10: 31-41. |
| [42] |
BOUARROUDJ E O, CHIKH S, ABDI S, et al. Thermal analysis during a rotational friction welding[J]. Applied Thermal Engineering, 2017, 110: 1543-1553. DOI:10.1016/j.applthermaleng.2016.09.067 |
| [43] |
SŁUAŻU ALEC A. Thermal effects in friction welding[J]. International Journal of Mechanical Sciences, 1990, 32(6): 467-478. DOI:10.1016/0020-7403(90)90153-A |
| [44] |
CHEN W L, YANG Y C, CHU S S. Estimation of heat generation at the interface of cylindrical bars during friction process[J]. Applied Thermal Engineering, 2009, 29(2-3): 351-357. DOI:10.1016/j.applthermaleng.2008.03.001 |
| [45] |
陈豪龙, 柳占立. 基于数据驱动模型求解热传导反问题[J]. 计算力学学报, 2021, 38(3): 272-279. CHEN H L, LIU Z L. Solving the inverse heat conduction problem based on data driven model[J]. Chinese Journal of Computational Mechanics, 2021, 38(3): 272-279. (in Chinese) |
| [46] |
GONÇALVES C V, CARVALHO S R, GUIMARÃES G. Application of optimization techniques and the enthalpy method to solve a 3D-inverse problem during a TIG welding process[J]. Applied Thermal Engineering, 2010, 30(16): 2396-2402. DOI:10.1016/j.applthermaleng.2010.06.009 |
| [47] |
杨晨, GROSS U. 基于热传导逆问题方法预测材料热物性参数[J]. 化工学报, 2005, 56(12): 2415-2420. YANG C, GROSS U. Estimation of thermal properties based on inverse heat conduction method[J]. CIESC Journal, 2005, 56(12): 2415-2420. DOI:10.3321/j.issn:0438-1157.2005.12.027 (in Chinese) |
| [48] |
WU X Y. Finite element simulation of linear friction welding[J]. Advanced Materials Research, 2011, 411: 126-129. DOI:10.4028/www.scientific.net/AMR.411.126 |
| [49] |
TASHKANDI M A. Finite element modeling of continuous drive friction welding of Al6061 alloy[J]. Materials Science—Poland, 2021, 39(1): 1-14. DOI:10.2478/msp-2021-0001 |
| [50] |
ASIF M M, SHRIKRISHANA K A, SATHIYA P. Finite element modelling and characterization of friction welding on UNS S31803 duplex stainless steel joints[J]. Engineering Science and Technology, An International Journal, 2015, 18(4): 704-712. DOI:10.1016/j.jestch.2015.05.002 |
| [51] |
张全忠, 张立文, 刘伟伟, 等. 连续驱动摩擦焊接过程的三维与二维数值模拟对比分析[J]. 焊接学报, 2006, 27(10): 105-108. ZHANG Q Z, ZHANG L W, LIU W W, et al. Comparison of 3D and 2D numerical simulation of continuous-drive friction welding process[J]. Transactions of the China Welding Institution, 2006, 27(10): 105-108. DOI:10.3321/j.issn:0253-360X.2006.10.028 (in Chinese) |
| [52] |
LEI B W, SHI Q Y, YANG L K, et al. Evolution of interfacial contact during low pressure rotary friction welding: A finite element analysis[J]. Journal of Manufacturing Processes, 2020, 56: 643-655. DOI:10.1016/j.jmapro.2020.05.034 |
| [53] |
KESSLER M, HARTL R, FUCHS A, et al. Simulation of rotary friction welding using a viscoelastic Maxwell model[J]. Science and Technology of Welding and Joining, 2021, 26(1): 68-74. DOI:10.1080/13621718.2020.1834683 |
| [54] |
ZHANG H, XIE J Q, LI C A, et al. Modelling and numerical analysis for rotatory friction welding of U75V steel rails[J/OL]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2024. DOI: 10.1177/14644207241242019.
|
| [55] |
MATTIE A A, EZDEEN S Y, KHIDHIR G I. Optimization of parameters in rotary friction welding process of dissimilar austenitic and ferritic stainless steel using finite element analysis[J/OL]. Advances in Mechanical Engineering, 2023, 15(7). DOI: 10.1177/16878132231186015.
|
| [56] |
张昌青, 师文辰, 罗德春, 等. 锥形端面对铝/钢连续驱动摩擦焊温度场的数值模拟研究[J]. 材料导报, 2022, 36(15): 21040043. ZHANG C Q, SHI W C, LUO D C, et al. Numerical simulation study on temperature field of continuous drive friction welding of aluminum/steel with conical terminal[J]. Materials Reports, 2022, 36(15): 21040043. DOI:10.11896/cldb.21040043 (in Chinese) |
| [57] |
WEN Q, LI W Y, GAO Y J, et al. Numerical simulation and experimental investigation of band patterns in bobbin tool friction stir welding of aluminum alloy[J]. The International Journal of Advanced Manufacturing Technology, 2019, 100(9): 2679-2687. |
| [58] |
HANNACHI N, KHALFALLAH A, LEITÃO C, et al. Comparison between ALE and CEL finite element formulations to simulate friction stir spot welding[M]//BOURAOUI T, BENAMEUR T, MEZLINI S, et al. Advances in mechanical engineering and mechanics Ⅱ. Cham: Springer, 2021: 277-284.
|
| [59] |
VAIRIS A, FROST M. Modelling the linear friction welding of titanium blocks[J]. Materials Science and Engineering: A, 2000, 292(1): 8-17. DOI:10.1016/S0921-5093(00)01036-4 |
| [60] |
ŁUKASZEWICZ A. Nonlinear numerical model of friction heating during rotary friction welding[J]. Journal of Friction and Wear, 2018, 39(6): 476-482. DOI:10.3103/S1068366618060089 |
| [61] |
HEPPNER E, SASAKI T, TROMMER F, et al. Model development for numerical analysis of the bonding strength for friction welded lightweight structures[J]. Finite Elements in Analysis and Design, 2024, 229: 104063. DOI:10.1016/j.finel.2023.104063 |
| [62] |
NIE L F, ZHANG L W, ZHU Z, et al. Microstructure evolution modeling of FGH96 superalloy during inertia friction welding process[J]. Finite Elements in Analysis and Design, 2014, 80: 63-68. DOI:10.1016/j.finel.2013.10.007 |
| [63] |
李伟, 楚志兵, 王环珠, 等. 三维微观组织模拟及其表征分析技术的研究进展[J]. 功能材料, 2020, 51(1): 1035-1042. LI W, CHU Z B, WANG H Z, et al. Research progress of three dimensional microstructure simulation and characterization analysis technology[J]. Journal of Functional Materials, 2020, 51(1): 1035-1042. DOI:10.3969/j.issn.1001-9731.2020.01.006 (in Chinese) |
| [64] |
REYES L A, GARZA C, DELGADO M, et al. Cellular automata modeling for rotary friction welding of Inconel 718[J]. Materials and Manufacturing Processes, 2022, 37(8): 877-885. DOI:10.1080/10426914.2021.2001514 |
| [65] |
MAALEKIAN M, CERJAK H. Thermal-phase transformation modelling and neural network analysis of friction welding of non-circular eutectoid steel components[J]. Weld World, 2009, 53(3): R44-R51. |
| [66] |
LIU W, WANG F F, YANG X W, et al. Upset prediction in friction welding using radial basis function neural network[J]. Advances in Materials Science and Engineering, 2013, 2013: 196382. |
| [67] |
PALANIVEL R, DINAHARAN I, LAUBSCHER R F. Application of an artificial neural network model to predict the ultimate tensile strength of friction-welded titanium tubes[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2019, 41(2): 111. DOI:10.1007/s40430-019-1613-2 |
| [68] |
KUNHIRUNBAWON S, SUWICHIEN N, JANTARASRICHA T. Friction welding parameter for AA6063 using ANFIS prediction[J]. The International Journal of Advanced Manufacturing Technology, 2023, 128(5): 2589-2597. |
| [69] |
CHIARANAI S, PITAKASO R, SETHANAN K, et al. Ensemble deep learning ultimate tensile strength classification model for weld seam of asymmetric friction stir welding[J]. Processes, 2023, 11(2): 434. DOI:10.3390/pr11020434 |
| [70] |
LU X H, MA C, YANG B H, et al. Prediction of the tensile strength of friction stir welded joints based on one-dimensional convolutional neural network[J]. Journal of Intelligent & Fuzzy Systems, 2023, 45(2): 2279-2288. |