轴承作为现代工业的基础零部件,普遍应用于旋转机械中。依据工作原理的不同,轴承大致可分为滚动轴承和滑动轴承2类。其中,滑动轴承是利用滑动摩擦原理支撑旋转部件并使承载面之间可作相对滑动的机械元件[1],优点是结构紧凑,所需安装空间小,回转精度高,此外由于无需滚动在高速旋转时的惯性力较小,比滚动轴承的运行更加平稳可靠且噪声小[2]。滑动轴承在精度要求高、径向尺寸小、非标尺寸等场景下具备独特优势,被广泛应用于航空航天、船舶制造等领域[3]。
随着现代机械向复杂化、精密化、高速化方向发展,轴承所处的工况条件也愈发严苛[4-6]。由于承载面之间发生相对滑动,在径向载荷作用下轴承可能发生磨损退化,进而产生转轴偏心过大、流体泄漏、内部构件干涉等问题[7]。当磨损积累至一定程度后会导致滑动轴承丧失部分甚至全部功能,影响整个机组的安全性和稳定性。例如1988年,秦岭发电厂5号机组因滑动轴承油膜失稳导致断轴毁机特大事故[8];2010年,大唐太原第二热电厂300MW机组增压风机因轴承振动过大造成停运[9];2023年,某船柴油机的航行试验因轴承磨损导致紧急停车[10]。因此,对运行过程中的滑动轴承磨损状态进行监测和预测,对于保障设备安全和降低维护成本有着重要意义。
近年来,相关学者逐渐开始重视对机械产品或设备的状态监测和预测工作[11]。目前关于轴承的状态监测和预测研究大多针对滚动轴承,全世界范围内也有诸多机械产品故障公开数据集供研究使用[12-14]。例如李恒等[15]通过短时Fourier变换从滚动轴承振动信号中得到二维时频图像,输入卷积神经网络中进行故障分类;Han等[16]提出一种基于深度迁移学习的旋转机械故障诊断框架。Wang等[17]使用相关向量机(relevance vector machine, RVM)从滚动轴承振动信号中提取退化特征,拟合经验指数模型来预测滚动轴承的剩余使用寿命。SKF智能轴承外部全部用传感器连接,对轴承整个运行过程进行监测甚至操控[18]。现有滚动轴承智能诊断方法通过从监测数据中提取特征,输入分类器或者回归器中进行故障诊断或寿命预测。
目前针对滑动轴承的研究主要集中于轴承润滑状态、油膜稳定性等问题[19-24]。磨损预测方面,Podra等[25]采用有限元方法对滑动轴承磨损过程进行仿真和静态预测,Jeon等[26]基于磨损试验对关节滑动轴承磨损量进行预测,Dai等[27]结合神经网络和有限元方法对磨损仿真结果实现瞬时输出。然而静态预测方法无法结合轴承实时状态数据,难以应用于复杂工况。滑动轴承自身结构特点使其数据特征分布与滚动轴承有较大差别,目前也鲜有关于滑动轴承的故障数据可使用。因此仍然有必要开展关于滑动轴承监测数据的特征分析,以制定切实可行的在线故障诊断与寿命预测方法。
本文针对滑动轴承的磨损退化和寿命预测问题,设计并建立了滑动轴承磨损试验台,使用自润滑石墨黄铜轴套开展磨损试验以及振动测量试验,采集轴承磨损过程的监测数据以及不同磨损状态下振动信号,对数据进行了特征分析;针对小样本量情况提出了一种基于多域特征和稀疏相关向量迭代指数退化(relevance-vector-based iterative exponential degradation, RV-IED) 的滑动轴承磨损智能诊断与寿命预测方法。特征工程方面,构建了能有效反映轴承退化趋势的多域特征:首先计算时域信号能量强度作为时域特征;其次对时域振动信号做Fourier变换并累积峰值带宽强度,通过主成分分析(principal component analysis, PCA) 降维提取第一主成分作为频域特征;最后引入动态时间规划(dynamic time warping, DTW) 算法计算不同幅值谱线之间的非线性距离,衡量频域波形的非线性特征。磨损诊断及寿命预测方面,基于RVM回归对新样本进行定量诊断,并基于稀疏相关向量对指数模型进行非线性加权拟合,进而预测轴承磨损深度变化趋势并得到剩余磨损寿命。利用实际试验中的滑动轴承磨损振动数据验证了该方法的有效性。
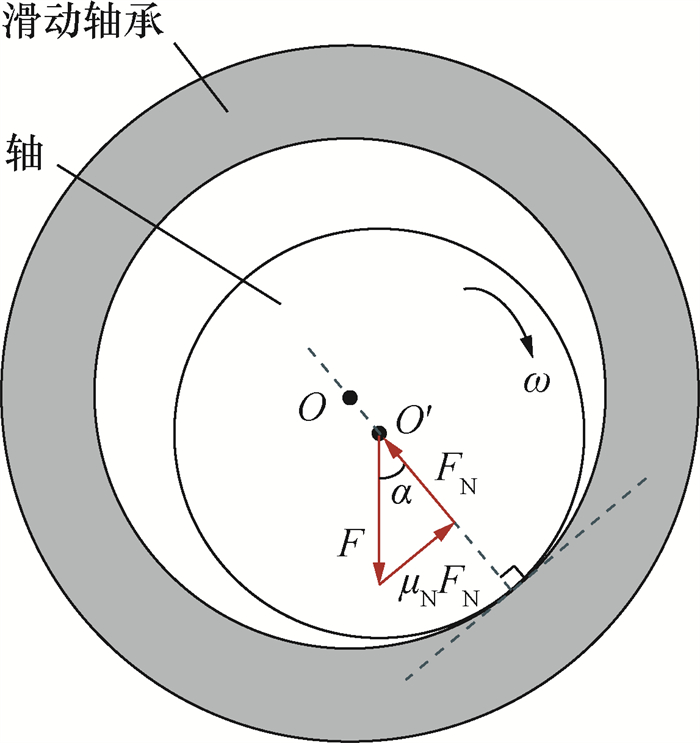
1 滑动轴承磨损试验滑动轴承的基本装配形式为转子-轴套配合,如图 1所示,轴承中心为O,转子在轴承的支承下绕轴向进行回转运动。转子质心为O′,转速为ω,受到径向力F作用。轴承内表面受到来自转轴的正压力FN和切向摩擦力μNFN,其中μN为表面摩擦系数。在润滑不充分的情况下,轴承接触位置易发生磨损,使得装配间隙增大,引起异常振动。相对于滚动轴承外圈-滚子-内圈的结构,滑动轴承结构简单,振动信号中的故障信息与前者存在较大差异。
|
| 图 1 滑动轴承基本装配形式 |
为定量研究轴承磨损状态下的振动信号与轴承磨损深度之间的关系,本文设计并搭建了滑动轴承磨损试验台。将磨损试验方案分为2部分。
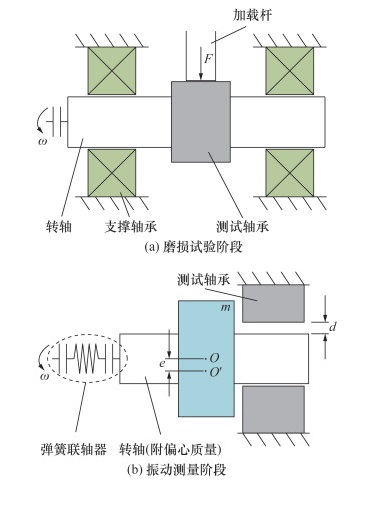
1) 滑动轴承磨损试验阶段,测试轴承内表面与转轴中段接触,轴承周向上保持不动,径向上受到来自于加载杆的固定载荷F作用,转轴两端使用圆柱滚子轴承作为支撑轴承,轴向和径向上受到固定约束,周向上保持恒速旋转,如图 2a所示。试验中使用自润滑石墨黄铜轴套作为测试轴承,与之配合的转轴材料为GCr15轴承钢。该阶段中测试轴承由健康状态转变为磨损状态。
|
| 图 2 磨损试验中的轴承装配示意图 |
2) 磨损轴承振动测量阶段,将已磨损的测试轴承固定在轴承座上作为转轴一端的支承件,转轴另一端使用弹簧联轴器与电机相连;转轴上附着偏心质量块(质量为m、偏心距为e),保持周向恒速旋转。如图 2b所示,轴颈与轴承之间的间隙为d,也即轴承承载面上磨损深度的最大值,称为最大磨损深度。
搭建的滑动轴承磨损试验台如图 3所示,气缸通过加载杆对测试轴承表面施加径向载荷,使用位移传感器测量加载杆的位移,用于表征试验过程中的轴承最大磨损深度;将PCB352C33单轴加速度传感器部署于轴承座表面以采集轴承振动信号。

|
| 图 3 滑动轴承磨损试验台 |
基于此试验台还可采集电机扭矩和轴承表面温度,相关传感器的采样设置如表 1所示。
| 类型 | 采样率/kHz | 采样时长/s | 采样间隔/s | 量程 | 测量误差 |
| 扭矩 | 1.0 | 1 | 10 | ±5 N·m | 0.01 N·m |
| 温度 | 1.0 | 1 | 10 | 0~400 ℃ | 10 ℃ |
| 径向 位移 |
1.0 | 1 | 10 | 0~5 mm | 1 μm |
| 振动信号 | 25.6 | 1 | 5 | ±490 m·s-2 | 5% |
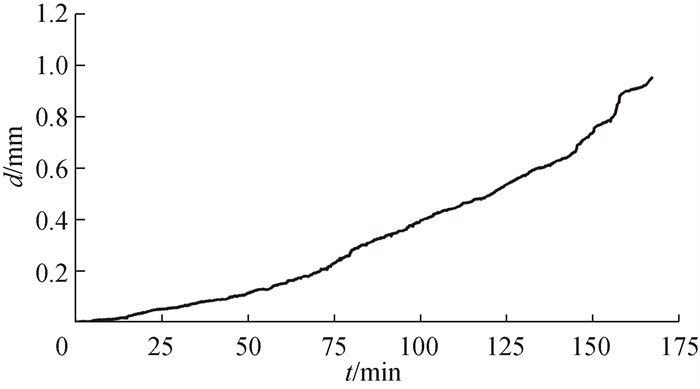
电机转速为3 500 r/min,径向载荷为150 N条件下进行170 min的磨损试验后,测试轴承实际磨损情况如图 4所示,由图可知,在轴承承载面上发生了一定程度的单侧磨损退化。

|
| 图 4 测试轴承磨损实物图 |
d可通过径向位移z计算,同时需考虑轴承温度T导致金属热胀冷缩的补偿项,计算关系如下:
| $ d=z_{0}-z+0.0006 \times\left(T-T_{0}\right) . $ | (1) |
其中:
|
| 图 5 最大磨损深度随磨损时间的变化 |
保持电机转速为
| $ d_{\text {list }}=\left\{\begin{array}{l} 0, 0.07, 0.24, 0.27, 0.41, 0.42, 0.53, \\ 0.69, 0.74, 0.76, 0.90, 0.95, 1.06, 1.16 \end{array}\right\} . $ | (2) |
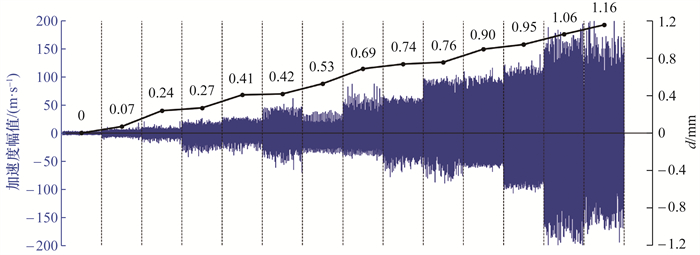
|
| 图 6 不同磨损深度下的轴承振动信号 |
2 振动信号特征工程 2.1 时频域分析
对于试验得到的含有
| $ \boldsymbol{X}=\left(\begin{array}{cccc} x_{1}^{(1)} & x_{1}^{(2)} & \cdots & x_{1}^{(c)} \\ x_{2}^{(1)} & x_{2}^{(2)} & \cdots & x_{2}^{(c)} \\ \vdots & \vdots & & \vdots \\ x_{N}^{(1)} & x_{N}^{(2)} & \cdots & x_{N}^{(c)} \end{array}\right). $ | (3) |
对式(3)的样本矩阵做离散Fourier变换得到频域幅值的样本矩阵为
| $ \boldsymbol{Y}=\left(\begin{array}{cccc} y_{1}^{(1)} & y_{1}^{(2)} & \cdots & y_{1}^{(p)} \\ y_{2}^{(1)} & y_{2}^{(2)} & \cdots & y_{2}^{(p)} \\ \vdots & \vdots & & \vdots \\ y_{N}^{(1)} & y_{N}^{(2)} & \cdots & y_{N}^{(p)} \end{array}\right). $ | (4) |
其中
| $ \begin{gather*} y_{n}^{(j)}=\left|\sum\limits_{k=1}^{c} x_{n}^{(k)} \exp \left(-\mathrm{i} \frac{2 {\rm{\mathsf{π}}}}{c} j(k-1)\right)\right|, \\ j=1, 2, \cdots, p \end{gather*} $ | (5) |
其中i为虚数单位。
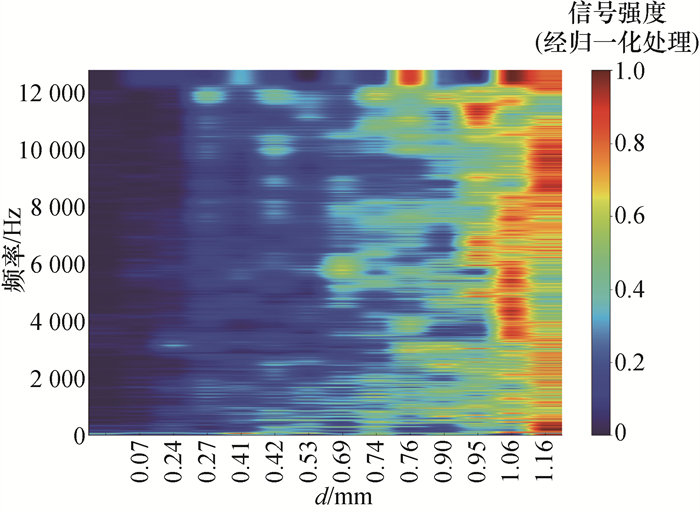
绘制YT的频谱图如图 7所示,为方便观察各频率分量的变化趋势,已沿横轴进行了归一化。横轴为不同的d值,纵轴为信号的不同频率分量,颜色代表经归一化处理后的信号强度。由图可知,随着d增大,不同频率分量下的信号强度整体呈增大趋势。
|
| 图 7 振动信号频谱图 |
本文考虑将时域或频域原始信号的波形相似度作为样本的非线性特征(在2.3节中进行详述)。因此需要考察将时域或频域原始信号作为样本、对应的
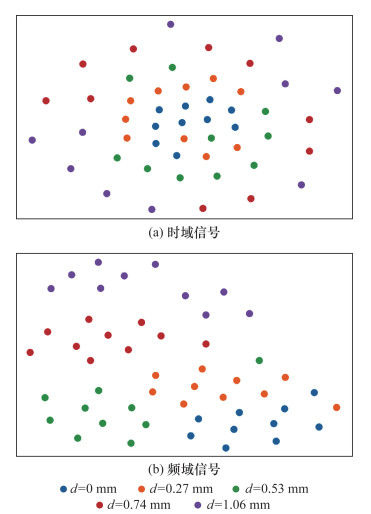
|
| 图 8 t-SNE降维可视化结果 |
2.2 时频域特征
在特征工程中,本文构造时域特征、频域特征、非线性特征结合的多域样本特征。时域特征方面,对式(3)的样本矩阵计算第n行的能量如下:
| $ f_{\text {energy }}=\frac{1}{s} \sum\limits_{k=1}^{c}\left(x_{n}^{(k)}\right)^{2} . $ | (6) |
其中s为信号采样率。
频域特征方面,对轴承频域幅值谱进行混合正态分布分解,如图 9所示,得到10个正态分布以及对应的均值
| $ \boldsymbol{f}=\left(\begin{array}{llll} f_1 & f_2 & \cdots & f_{10} \end{array}\right)^{\mathrm{T}} . $ | (7) |
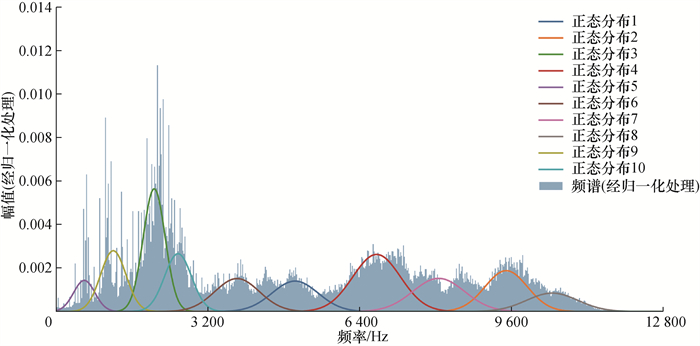
|
| 图 9 频谱多正态分布分解 |
其中任一元素
为了从式(7)所示向量中提取可反映轴承退化过程的信息,需要对f进行PCA降维,并选择第一主成分作为频域特征fPCA。PCA作为一种常用的数据降维手段,基于数据方差最大原则对高维数据进行投影降维,其优化目标如下:
| $ F_{\text {target }}=\underset{\beta}{\arg \min }\|\boldsymbol{f}-g(\boldsymbol{\beta})\|_{2} . $ | (8) |
其中:β为降维后的频域特征样本,g(β)为重构样本。PCA算法流程如图 10所示。

|
| 图 10 PCA降维算法 |
2.3 动态时间规划
对于式(4)中每行向量所表示的频域波形,目标是衡量第
| $ D_{\text {Euclidean }}\left(\boldsymbol{y}_{u}, \boldsymbol{y}_{v}\right)=\sqrt{\sum\limits_{j=1}^{p}\left(y_{u}^{(j)}-y_{v}^{(j)}\right)^{2}} \text {, } $ | (9) |
| $ D_{\text {cosine }}\left(\boldsymbol{y}_{u}, \boldsymbol{y}_{v}\right)=\frac{\sum\limits_{j=1}^{p} y_{u}^{(j)} y_{v}^{(j)}}{\sqrt{\sum\limits_{j=1}^{p}\left(y_{u}^{(j)}\right)^{2}} \cdot \sqrt{\sum\limits_{l=1}^{p}\left(y_{v}^{(l)}\right)^{2}}} . $ | (10) |
由于"维数灾难"问题,在高维空间中数据点的
| $ \begin{gathered} D_{\text {DTW }}^{(u, v)}(j, l)=D\left(y_u^{(j)}, y_v^{(j)}\right)+\min \left\{D_{\text {DTW }}^{(u, v)}(j-1, l),\right. \\ \left.D_{\text {DTW }}^{(u, v)}(j, l-1), D_{\text {DTW }}^{(u, v)}(j-1, l-1)\right\} . \end{gathered} $ | (11) |
其中
为减小算法的时间开销和内存开销,对式(4)所示的频域样本矩阵每20列进行求和,得到一个尺寸为
| $ f_{\text {DTW }}=D_{\text {DTW }}^{(n, 1)}(p / 20, p / 20) . $ | (12) |
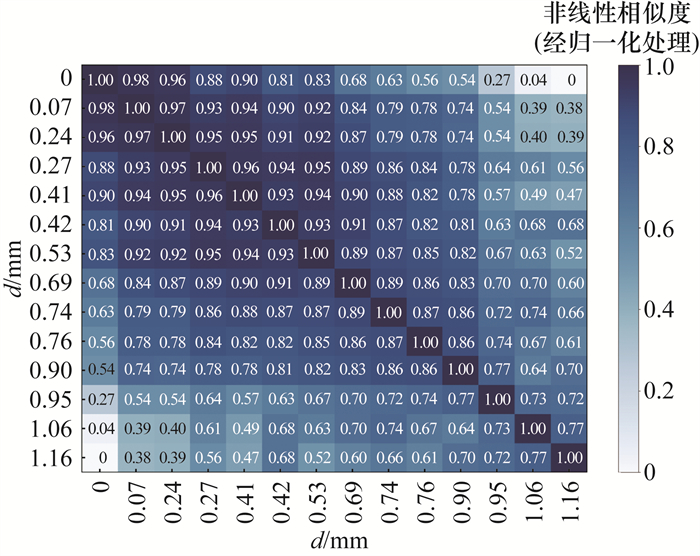
|
| 图 11 基于DTW的相似度矩阵(经归一化处理) |
因此提出多域特征的表达方式如下:
| $ \boldsymbol{f}_{\text {mix }}=\left(\begin{array}{lll} f_{\text {energy }} & f_{\text {PCA }} & f_{\text {DTW }} \end{array}\right) . $ | (13) |
本文提出基于稀疏相关向量的迭代指数退化预测方法,使用相关向量回归对新特征样本对应的最大磨损深度进行在线诊断,并从历史生命周期数据中提取具有稀疏性的相关向量拟合指数退化模型,对轴承的磨损深度变化趋势进行预测。
3.1 相关向量机RVM是使用Bayes推理得到回归和分类的机器学习方法[30-32]。相对于支持向量机(support vector machine, SVM)而言,RVM通常会产生更加稀疏的模型,极大提升了数据处理速度。此外RVM对于给定输入可以给出概率型输出。
从第1章滑动轴承磨损试验中采集到的监测数据和代表退化程度的对应目标值,可基于机器学习模型进行监督训练,得到监测数据与标签之间的非线性映射关系。在监督学习中给定数据对{xn, dn}n=1N,其中:xn为输入矢量;dn为标签,在本文所研究问题中即为最大磨损深度。遵循标准概率公式,并假设从有噪声模型中获取目标值如下:
| $ d_{n}=y\left(\boldsymbol{x}_{n} ; \boldsymbol{w}\right)+\varepsilon_{n} . $ | (14) |
其中:w为权重矢量;εn为噪声,独立采样于均值为0、方差为σ2的Guass分布。因此
| $ p\left(d_{n} \mid \boldsymbol{x}\right)=\mathcal{N}\left(d_{n} \mid y\left(\boldsymbol{x}_{n}\right), \sigma^{2}\right) . $ | (15) |
其中式(15)右边项指均值为
| $ y(\boldsymbol{x} ; \boldsymbol{w})=\sum\limits_{i=1}^{N} w_{i} K\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right)+w_{0} . $ | (16) |
其中
| $ p\left(\boldsymbol{d} \mid \boldsymbol{w}, \sigma^{2}\right)=\left(2 {\rm{\mathsf{π}}} \sigma^{2}\right)^{-N / 2} \exp \left(-\frac{1}{2 \sigma^{2}}\|d-\varPhi \boldsymbol{w}\|_{2}^{2}\right) $ | (17) |
其中,
在w中选择常见的零均值Guass先验分布以获得更平滑的函数如下:
| $ p(\boldsymbol{w} \mid \boldsymbol{\alpha})=\prod\limits_{i=0}^{N} \mathcal{N}\left(w_{i} \mid 0, \alpha_{i}^{-1}\right) . $ | (18) |
其中α为超参数向量,且每个α i-1与权重wi单独关联。
根据Bayes准则,计算权重参数的后验分布为
| $ \begin{gather*} p\left(\boldsymbol{w} \mid \boldsymbol{d}, \boldsymbol{\alpha}, \sigma^{2}\right)= \\ p\left(\boldsymbol{d} \mid \boldsymbol{w}, \sigma^{2}\right) \cdot p(\boldsymbol{w} \mid \boldsymbol{\alpha}) / p\left(\boldsymbol{d} \mid \boldsymbol{\alpha}, \sigma^{2}\right)= \\ (2 {\rm{\mathsf{π}}})^{(N+1) / 2}|\varSigma|^{-1 / 2} \exp \left(-\frac{1}{2}(\boldsymbol{w}-\boldsymbol{\mu})^{\mathrm{T}} \varSigma^{-1}(\boldsymbol{w}-\boldsymbol{\mu})\right) . \end{gather*} $ | (19) |
同时上式服从Guass分布
| $ \boldsymbol{\mu}=\sigma^{-2} \varSigma \varPhi^{\mathrm{T}} \boldsymbol{d}, $ | (20) |
| $ \varSigma=\left(\sigma^{-2} \varPhi^{\mathrm{T}} \varPhi+\boldsymbol{A}\right)^{-1} . $ | (21) |
其中对角阵
对权重向量积分得到边缘似然函数
| $ \begin{gather*} \ln p\left(\boldsymbol{d} \mid \boldsymbol{\alpha}, \sigma^{2}\right)=\ln \int p\left(\boldsymbol{d} \mid \boldsymbol{w}, \sigma^{2}\right) p(\boldsymbol{w} \mid \boldsymbol{\alpha}) \mathrm{d} \boldsymbol{w}= \\ \quad-\frac{1}{2}\left[N \ln 2 {\rm{\mathsf{π}}}+\ln |\boldsymbol{C}|+\boldsymbol{d}^{\mathrm{T}} \boldsymbol{C}^{-1} \boldsymbol{d}\right] . \quad \end{gather*} $ | (22) |
其中
| $ \begin{gather*} p\left(d^{\prime} \mid \boldsymbol{d}, \boldsymbol{\alpha}_{*}, \sigma_{*}^{2}\right)= \\ \int p\left(d^{\prime} \mid \boldsymbol{w}, \sigma^{2}\right) p\left(\boldsymbol{w} \mid \boldsymbol{d}, \boldsymbol{\alpha}_{*}, \sigma_{*}^{2}\right) \mathrm{d} \boldsymbol{w}= \\ \mathcal{N}\left(d^{\prime} \mid \boldsymbol{\mu}_{*}^{\mathrm{T}} K\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right), \sigma_{*}^{2}+K\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)^{\mathrm{T}} \varSigma_{*} K\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)\right) . \end{gather*} $ | (23) |
由此可得新输入样本对应的输出均值及方差。
3.2 基于稀疏相关向量的迭代指数退化预测RVM在训练时通过最大化目标函数式(22)对
采用指数模型作为滑动轴承磨损退化模型,用以刻画轴承d随t的变化趋势[33]。数学公式如下:
| $ d(t)=a \exp (b t)-a . $ | (24) |
其中a、b为待定系数,由应用场景中的试验数据拟合得到。本文的拟合算法选用非线性最小二乘法。
本文提出基于稀疏相关向量的迭代指数退化预测方法,在每次进行磨损深度诊断时,使用多项式核RVM对当前样本及历史样本迭代提取相关向量用于拟合指数退化模型,同时考虑到不同样本对模型拟合贡献的差异,将式(18)中相关向量的αi-1超参项作为权重值赋予对应样本。
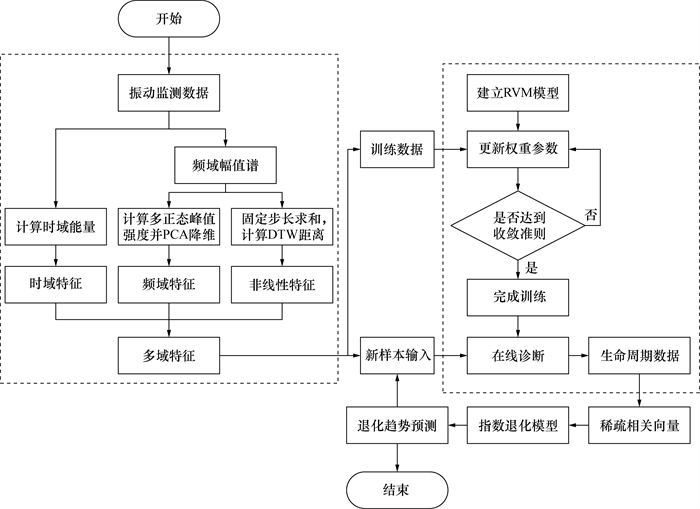
因此,本文所提的基于多域特征和RV-IED的滑动轴承磨损诊断与寿命预测方法流程如图 12所示。
|
| 图 12 基于多域特征和RV-IED的磨损诊断与寿命预测算法 |
4 实例应用验证与结果分析
为验证本文所提方法的有效性和实用性,针对第1章滑动轴承磨损试验中得到的、d=0~1.16 mm的14个磨损轴承样件的振动信号进行磨损诊断与寿命预测,并与传统方法进行对比。其中采样间隔为5 s,采样长度为1 s,采样频率为25.6 kHz,数据集中包含621个样本。
4.1 磨损深度诊断本文采用的模型诊断量化误差的评价指标包括均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均相对误差(mean relative error,MRE),其中MRE不计算标签为0的数据。相关计算公式如下:
| $ e_{\mathrm{RMSE}}=\sqrt{\frac{1}{N_{\text {test }}} \sum\limits_{i=1}^{N_{\text {test }}}\left[d_{i}^{\prime}-d_{i}\right]^{2}}, $ | (25) |
| $ e_{\mathrm{MAE}}=\frac{1}{N_{\text {test }}} \sum\limits_{i=1}^{N_{\text {test }}}\left|d_{i}^{\prime}-d_{i}\right|, $ | (26) |
| $ e_{\mathrm{MRE}}=\frac{1}{N_{\text {test }}} \sum\limits_{i=1}^{N_{\text {test }}}\left|\frac{d_{i}^{\prime}-d_{i}}{d_{i}}\right| \times 100 \% . $ | (27) |
其中:
将整个数据集按1∶1的比例随机划分为训练集和测试集,对应的14个标签如式(2)所示。RVM回归采用径向基核函数如下:
| $ K\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right)=\exp \left(-\gamma\left\|\boldsymbol{x}-\boldsymbol{x}_{i}\right\|_{2}^{2}\right) . $ | (28) |
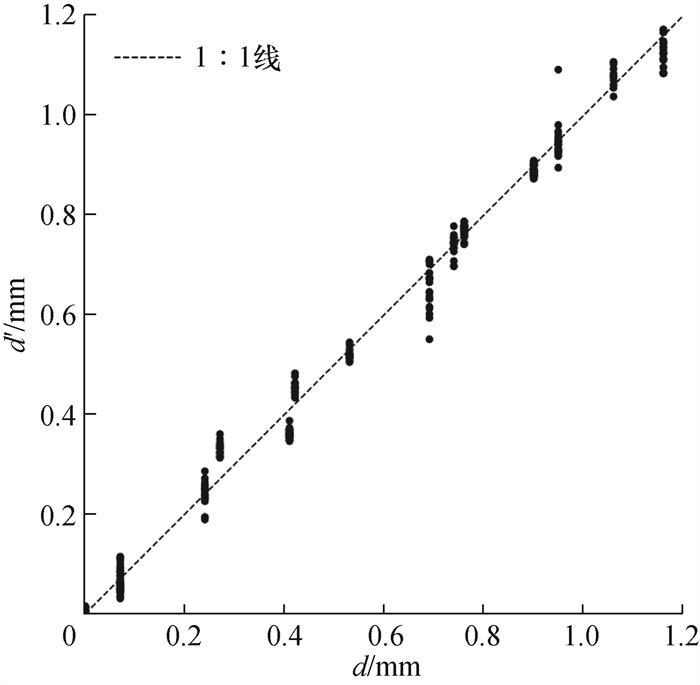
所提方法对测试集的磨损深度诊断结果如图 13所示。诊断结果越靠近1∶1线说明模型越准确,由图可知,模型输出值分布在1∶1线附近,表明模型输出的精确度较高。
|
| 图 13 最大磨损深度诊断结果 |
对照方法采用提取时域、频域常用特征后进行PCA压缩到三维(保持与所提多域特征维度一致),输入RVM或支持向量机(SVM)中得到诊断结果。信号特征包括峰值、绝对平均值、方差、标准差、均方根、能量、偏度、峭度、波形因子、峰值因子、脉冲因子、裕度因子这12个时域特征(见表 2)以及文[34]中的13个频域特征。
| 特征 | 计算公式 |
| 峰值 | |
| 绝对平均值 | |
| 方差 | |
| 标准差 | |
| 均方根 | |
| 能量 | |
| 偏度 | |
| 峭度 | |
| 波形因子 | |
| 峰值因子 | |
| 脉冲因子 | |
| 裕度因子 | |
| 注: | |
由于训练集与测试集采用随机划分的方式,为减小随机误差,本文重复进行3次数据集划分,在此基础上进行每种方法的诊断试验,按照式(25)—(27)计算误差指标,取均值作为最终结果。其中,4种对照方法如下:
对照方法Ⅰ:提取12个时域特征进行PCA降维,采用RVM进行诊断;
对照方法Ⅱ:提取13个频域特征进行PCA降维,采用RVM进行诊断;
对照方法Ⅲ:提取25个时域和频域特征进行PCA降维,采用RVM进行诊断;
对照方法Ⅳ:提取25个时域和频域特征进行PCA降维,采用SVM进行诊断。
诊断结果对比如表 3所示,所提方法的3种误差指标均优于其余4种对照方法,证明了本文所提方法可有效表征轴承磨损信息并进行磨损诊断,且表现优于对照组中基于传统时域、频域特征的诊断方法;此外,在本文的研究场景中,SVM模型的精度低于RVM。
| 诊断方法 | RMSE | MAE | MRE/% |
| 所提方法 | 0.035 | 0.027 | 9.8 |
| 对照方法Ⅰ | 0.046 | 0.033 | 11.7 |
| 对照方法Ⅱ | 0.060 | 0.044 | 12.2 |
| 对照方法Ⅲ | 0.050 | 0.037 | 12.0 |
| 对照方法Ⅳ | 0.071 | 0.056 | 23.3 |
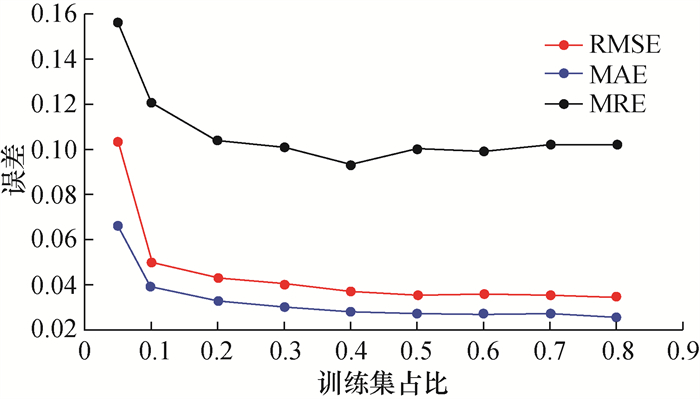
接着围绕训练数据量在整个数据集中的占比对模型精度的影响展开分析。设定训练集占比为5%~ 80%的系列值进行训练和测试。重复试验3次,结果如图 14所示。从结果可见,随着训练集占比的增加,模型误差整体呈下降趋势,但30%~80%之间的变化趋势并不明显,其中MRE处于10%附近。因此,在不需要大量样本的情况下,所提方法便可达到较高的诊断精度,说明该方法可适用于小样本量的情况。
|
| 图 14 训练集占比对误差影响趋势 |
4.2 磨损退化趋势及剩余使用寿命预测
将图 5所示轴承实际磨损深度变化曲线作为拟预测对象,曲线末端对应d为1.01 mm,t为170 min。在t时刻获取轴承振动信号,输入所建立模型诊断得到d′,经过多次诊断后,结合所得到的所有诊断结果(t, d′),基于多项式核RVM回归提取相关向量,并将αi-1作为向量权重,基于非线性最小二乘法对式(24)中的指数模型进行拟合。多项式核函数如下:
| $ K\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right)=\left(\alpha \boldsymbol{x}^{\mathrm{T}} \boldsymbol{x}_{i}+c\right)^{h} . $ | (29) |
其中h为多项式指数,本文取h=3。
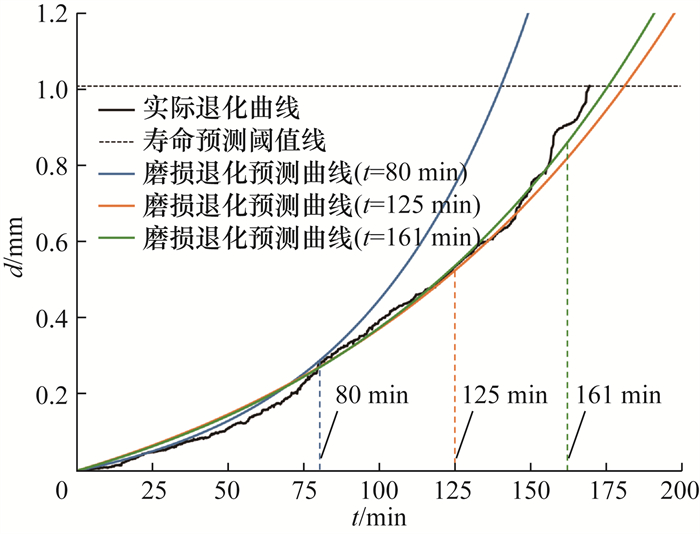
对经历了
|
| 图 15 磨损趋势预测 |
当滑动轴承磨损达到一定程度,即
| $ t_{\text {end }}=\frac{1}{b} \ln \left(\frac{d_{\text {threshold }}}{a}+1\right) . $ | (30) |
tend与t之间的差值为剩余使用寿命RUL。
| $ R_{\mathrm{UL}}=t_{\mathrm{end}}-t . $ | (31) |
计算各个时刻预测寿命的绝对误差如下:
| $ e_{\text {rror }}=t_{\text {end }}-t_{\text {life }} . $ | (32) |
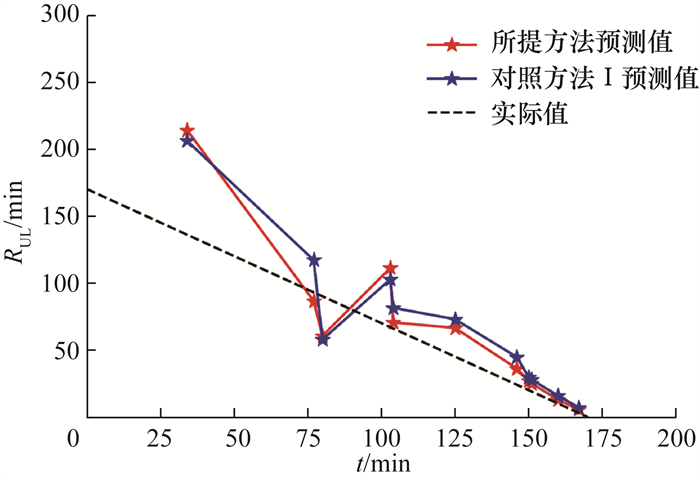
在4.1节所采用的4种对照方法中,方法Ⅰ的RMSE、MAE、MRE均最小。本节使用对照方法Ⅰ的诊断结果基于常规最小二乘法拟合指数模型,得到的预测结果如图 16所示,由图可知,初期RUL预测值与实际值差异较大,而随着t增大,二者趋于一致。
|
| 图 16 剩余使用寿命预测 |
预测误差如表 4所示,由表可知,随着t增大,本文所提方法和对照方法Ⅰ的error均减小,且所提方法的收敛速度更快。
| min | |||||||||||||||||||||||||||||
| t | 实际RUL | error | |||||||||||||||||||||||||||
| 所提方法 | 对照方法Ⅰ | ||||||||||||||||||||||||||||
| 34 | 136 | 78.1 | 70.1 | ||||||||||||||||||||||||||
| 77 | 93 | —6.4 | 24.1 | ||||||||||||||||||||||||||
| 80 | 90 | —29.5 | —32.2 | ||||||||||||||||||||||||||
| 103 | 67 | 44.1 | 35.6 | ||||||||||||||||||||||||||
| 104 | 66 | 4.5 | 15.4 | ||||||||||||||||||||||||||
| 125 | 55 | 11.4 | 17.9 | ||||||||||||||||||||||||||
| 146 | 24 | 12.1 | 20.7 | ||||||||||||||||||||||||||
| 150 | 20 | 7.0 | 9.6 | ||||||||||||||||||||||||||
| 151 | 19 | 6.0 | 8.8 | ||||||||||||||||||||||||||
| 160 | 10 | 2.9 | 5.9 | ||||||||||||||||||||||||||
| 167 | 3 | 2.4 | 4.0 | ||||||||||||||||||||||||||
由于RUL预测涉及多个时间点,且通常希望实现越接近失效时刻的预测精度越高,因此本文采用累积相对精度CRA[35]对预测精度进行评价。假设进行了K次预测,则CRA的计算公式如下:
| $ C_{\mathrm{RA}}=\sum\limits_{i=1}^{K} \omega_{i}\left(1-\frac{\left|R_{\mathrm{UL}, \text { label }}^{(i)}-\hat{R}_{\mathrm{UL}}^{(i)}\right|}{R_{\mathrm{UL}, \text { label }}^{(i)}}\right) . $ | (33) |
其中:
所提磨损预测方法是一个迭代过程,预测早期由于可用拟合数据少,误差较大;随着时间推移,精度会呈逐渐提高的趋势,绝对误差趋于0。从降低产品检修维护成本以及减少失效带来的损失方面来看,通常期望更接近失效时刻的剩余寿命预测精度是更高的,以进行有效的预测性维护,防止轴承失效带来的重大损失。
本文所提方法主要面向于小样本量情况下的诊断问题,适用样本量规模建议控制在1×104个以内。所采用的RVM模型属于浅层机器学习算法,与深度学习相比,需要在整个数据集上进行计算,当样本量增加时计算时间和计算成本将大幅增加,且可能无法捕获大规模数据集上的复杂特征关系。本文所提方法比深度学习方法的优势在于特征与模型具有物理意义和理论支持,在小样本量情况下即可获得较高可信度的结果。
5 结论本文设计并开展了滑动轴承磨损退化试验,基于振动监测信号实现了滑动轴承磨损状态的智能诊断与寿命预测。对轴承振动信号分别提取了时域特征、频域特征以及非线性特征以构建能反映轴承退化过程的多域特征,提出适用于小样本量情况的RV-IED磨损诊断与寿命预测方法,可在线诊断滑动轴承最大磨损深度,对轴承磨损退化趋势进行预测并得到剩余使用寿命。验证试验中诊断精度(平均相对误差)为10%左右;寿命预测误差(绝对误差)随着拟合数据的增多而减少,并随着时间推移呈现趋于0的变化趋势。在磨损诊断与寿命预测任务中所提方法精度均超过了基于传统时域、频域特征的诊断方法。
对于智能诊断方法,更加丰富的训练数据通常可以使模型得到更好的训练,因此仍需采集更多磨损数据以得到更合适的模型。此外,轴承加速退化试验与轴承自然退化过程的数据特征可能存在一定差别,采集产品在自然运行状态下的生命周期数据也有助于进一步探索轴承故障智能诊断与寿命预测方法。
| [1] |
尹延国, 焦明华, 解挺, 等. 滑动轴承材料的研究进展[J]. 润滑与密封, 2006(5): 183-187. YIN Y G, JIAO M H, XIE T, et al. Research progress in sliding bearing materials[J]. Lubrication Engineering, 2006(5): 183-187. DOI:10.3969/j.issn.0254-0150.2006.05.060 (in Chinese) |
| [2] |
DU F M, LI D W, SA X X, et al. Overview of friction and wear performance of sliding bearings[J]. Coatings, 2022, 12(9): 1303. DOI:10.3390/coatings12091303 |
| [3] |
SHI G Q, YU X D, MENG H, et al. Effect of surface modification on friction characteristics of sliding bearings: A review[J]. Tribology International, 2023, 177: 107937. DOI:10.1016/j.triboint.2022.107937 |
| [4] |
WANG L P, KONG X Y, YU G, et al. Error estimation and cross-coupled control based on a novel tool pose representation method of a five-axis hybrid machine tool[J]. International Journal of Machine Tools and Manufacture, 2022, 182: 103955. DOI:10.1016/j.ijmachtools.2022.103955 |
| [5] |
LUO R Z, CAO P, DAI Y Z, et al. Rotating machinery fault diagnosis theory and implementation[J]. Instrument Technique and Sensor, 2014(3): 107-110. DOI:10.3969/j.issn.1002-1841.2014.03.035 |
| [6] |
朱斌, 王立平, 吴军, 等. 面向不完全维修数控机床的可靠性建模与评估[J]. 清华大学学报(自然科学版), 2022, 62(5): 965-970. ZHU B, WANG L P, WU J, et al. Reliability modeling and evaluation of CNC machine tools for a general state of repair[J]. Journal of Tsinghua University(Science and Technology), 2022, 62(5): 965-970. (in Chinese) |
| [7] |
李云鹤, 谭雁清, 马廉洁, 等. 陶瓷滑动轴承磨损可靠性建模及仿真分析[J]. 润滑与密封, 2023, 48(7): 167-171. LI Y H, TAN Y Q, MA L J, et al. Wear reliability modeling and simulation analysis of ceramic plain bearing[J]. Lubrication Engineering, 2023, 48(7): 167-171. DOI:10.3969/j.issn.0254-0150.2023.07.024 (in Chinese) |
| [8] |
钟群鹏, 张峥, 有移亮. 我国安全生产(含安全制造)的科学发展若干问题[J]. 机械工程学报, 2007, 43(1): 7-18. ZHONG Q P, ZHANG Z, YOU Y L. Several issues of scientific development of safety production (including safety manufacturing) in China[J]. Journal of Mechanical Engineering, 2007, 43(1): 7-18. DOI:10.3321/j.issn:0577-6686.2007.01.003 (in Chinese) |
| [9] |
刘小龙. 轴流风机轴承损坏事故分析[J]. 山西科技, 2010, 25(3): 115. LIU X L. Analysis on the damage to the bearing of axial flow fans[J]. Shanxi Science and Technology, 2010, 25(3): 115. (in Chinese) |
| [10] |
陈日权, 王磊, 李唐, 等. 某船柴油机轴瓦异常磨损故障原因分析[J]. 船舶物资与市场, 2023, 31(10): 88-90. CHEN R Q, W L, L T, et al. Analysis of abnormal wear causes in diesel engine shaft bushings on a certain ship[J]. Marine Equipment/Materials and Marketing, 2023, 31(10): 88-90. (in Chinese) |
| [11] |
王立平, 朱斌, 吴军, 等. 基于贝叶斯网络的盘式刀库故障分析[J]. 吉林大学学报(工学版), 2022, 52(2): 280-287. WANG L P, ZHU B, WU J, et al. Fault analysis of circular tool magazine based on Bayesian network[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(2): 280-287. (in Chinese) |
| [12] |
雷亚国, 韩天宇, 王彪, 等. XJTU-SY滚动轴承加速寿命试验数据集解读[J]. 机械工程学报, 2019, 55(16): 1-6. LEI Y G, HAN T Y, WANG B, et al. XJTU-SY rolling element bearing accelerated life test datasets: A tutorial[J]. Journal of Mechanical Engineering, 2019, 55(16): 1-6. (in Chinese) |
| [13] |
NECTOUX P, GOURIVEAU R, MEDJAHER K, et al. PRONOSTIA: An experimental platform for bearings accelerated degradation tests[C]//Proceedings of International Conference on Prognostics and Health Management. Denver, Colorado, United States: IEEE, 2012: 1-8.
|
| [14] |
SAXENA A, GOEBEL K, SIMON D, et al. Damage propagation modeling for aircraft engine run-to-failure simulation[C]//Proceedings of 2008 International Conference on Prognostics and Health Management. Denver, CO, USA: IEEE, 2008.
|
| [15] |
李恒, 张氢, 秦仙蓉, 等. 基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J]. 振动与冲击, 2018, 37(19): 124-131. LI H, ZHANG Q, QIN X R, et al. Fault diagnosis method for rolling bearings based on short-time Fourier transform and convolution neural network[J]. Journal of Vibration and Shock, 2018, 37(19): 124-131. (in Chinese) |
| [16] |
HAN T, LIU C, YANG W G, et al. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application[J]. ISA Transactions, 2020, 97: 269-281. DOI:10.1016/j.isatra.2019.08.012 |
| [17] |
WANG B, LEI Y G, LI N P, et al. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings[J]. IEEE Transactions on Reliability, 2020, 69(1): 401-412. DOI:10.1109/TR.2018.2882682 |
| [18] |
雒建斌. 影响制造业发展的新技术[J]. 中国市场监管研究, 2020(10): 12-14. LUO J B. New techniques of influencing the development of manufacturing industry[J]. Research on ChinaMarket Regulation, 2020(10): 12-14. (in Chinese) |
| [19] |
李健, 程先华. 动静压支承滑动轴承性能分析[J]. 上海交通大学学报, 2006, 40(12): 2026-2029. LI J, CHENG X H. The analysis of dynamic and static back journal bearing's performance[J]. Journal of Shanghai Jiaotong University, 2006, 40(12): 2026-2029. DOI:10.3321/j.issn:1006-2467.2006.12.003 (in Chinese) |
| [20] |
CHASALEVRIS A C, NIKOLAKOPOULOS P G, PAPADOPOULOS C A. Dynamic effect of bearing wear on rotor-bearing system response[J]. Journal of Vibration and Acoustics, 2013, 135(1): 011008. DOI:10.1115/1.4007264 |
| [21] |
SUN J, ZHU X L, ZHANG L, et al. Effect of surface roughness, viscosity-pressure relationship and elastic deformation on lubrication performance of misaligned journal bearings[J]. Industrial Lubrication and Tribology, 2014, 66(3): 337-345. DOI:10.1108/ilt-12-2011-0110 |
| [22] |
ENGEL T, LECHLER A, VERL A. Sliding bearing with adjustable friction properties[J]. CIRP Annals, 2016, 65(1): 353-356. DOI:10.1016/j.cirp.2016.04.084 |
| [23] |
REN G J. A new method to calculate water film stiffness and damping for water lubricated bearing with multiple axial grooves[J]. Chinese Journal of Mechanical Engineering, 2020, 33(1): 72. DOI:10.1186/s10033-020-00492-w |
| [24] |
TOFIGHI-NIAKI E, SAFIZADEH M S. Dynamic of a flexible rotor-bearing system supported by worn tilting journal bearings experiencing rub-impact[J]. Lubricants, 2023, 11(5): 212. |
| [25] |
PÕDRA P, ANDERSSON S. Simulating sliding wear with finite element method[J]. Tribology International, 1999, 32(2): 71-81. |
| [26] |
JEON H G, CHO D H, YOO J H, et al. Wear prediction of earth-moving machinery joint bearing via correlation between wear coefficient and film parameter: Experimental study[J]. Tribology Transactions, 2018, 61(5): 808-815. |
| [27] |
DAI J Z, TIAN L. A novel prognostic method for wear of sliding bearing based on SFENN[C]//Proceedings of the 6th International Conference on Intelligent Robotics and Applications. Singapore: Springer, 2023.
|
| [28] |
HASTIE T, TIBSHIRANI R, FRIEDMAN J. The elements of statistical learning: data mining, inference, and prediction[M]. 2nd ed. New York: Springer, 2009.
|
| [29] |
MVLLER M. Dynamic time warping[M]//MVLLER M. Information retrieval for music and motion. Berlin Heidelberg: Springer, 2007: 69-84.
|
| [30] |
TIPPING M E. The relevance vector machine[C]//Proceedings of the 12th International Conference on Neural Information Processing Systems. Cambridge, UK: NIPS, 1999: 652-658.
|
| [31] |
TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1: 211-244. |
| [32] |
TIPPING M E, FAUL A C. Fast marginal likelihood maximisation for sparse Bayesian models[C]//Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics. Key West, FL, USA: PMLR, 2003: 276-283.
|
| [33] |
HE W, WILLIARD N, OSTERMAN M, et al. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method[J]. Journal of Power Sources, 2011, 196(23): 10314-10321. |
| [34] |
LEI Y G, HE Z J, ZI Y Y, et al. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs[J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2280-2294. |
| [35] |
SAXENA A, CELAYA J, SAHA B, et al. Metrics for offline evaluation of prognostic performance[J]. International Journal of Prognostics and Health Management, 2010, 1(1): 1-20. |



