2. 中国地质大学(北京) 工程技术学院, 北京 100083
2. School of Engineering and Technology, China University of Geosciences (Beijing), Beijing 100083, China
随着科技的不断进步,人类对海洋资源的利用和对海洋环境的探索迈入了新阶段,设计出了各式各样的水下探测装备。其中水下滑翔机的概念于1989年由海洋学家Stommel[1]首次提出,并引起世界范围内的广泛关注,各国开始陆续开展水下滑翔机的研制工作。目前成功研制并广泛应用的水下滑翔机包括Slocum[2]、Seaglider[3]、Spray[4]、“海翼”[5]和“海燕”[6]等型号。水下滑翔机通常通过改变排水体积调节净浮力,实现上浮/下潜切换;通过改变内部可动质量块的位置,实现姿态调整;无需外部主动推进即可实现空间运动,具备噪声小、续航能力强等优点,非常适合大范围且长期的水下探测任务。
目前,已有学者围绕水下滑翔机宏观组成开展设计优化,例如通过优化水下滑翔机的结构组成[7-9]、控制参数[10-14]、水动力外形[15-17]等,有效提升其航速、能量利用率、静稳定性等性能。然而,针对水下滑翔机表面微观形貌开展参数优化的研究较少,但目前已有研究分析了表面微观形貌对物体水动力性能的影响, 如胡海豹等[18]针对回转体开展高速水洞实验,分析了回转体表面不同形状沟槽的减阻效果;杨海霞[19]利用FLUENT软件探究了水下航行器表面沟槽的形状、尺寸与其减阻效果之间的关系;王晋军等[20]基于流体实验,研究了水流经沟槽板时的流场速度分布、紊动情况;张帅[21]采用计算流体力学(CFD)方法定量分析了含沟槽方形管道在流体经过时所受阻力,确定了最佳沟槽形状,且将该形状沟槽应用于水下滑翔机表面时减阻率可达2%。
因此,本文将以提升水下滑翔机航速和静稳定性、降低能耗为目标,开展翼面沟槽参数的多目标设计优化。该项研究将进一步丰富水下滑翔机优化设计思路,为水下滑翔机性能改进提供理论指导。
1 水下滑翔机翼面沟槽设计本文以“海燕-Ⅱ”型水下滑翔机为基本原型开展研究,该水下滑翔机主要结构组成包括机体、机翼、可动质量块、外油囊等,如图 1所示。
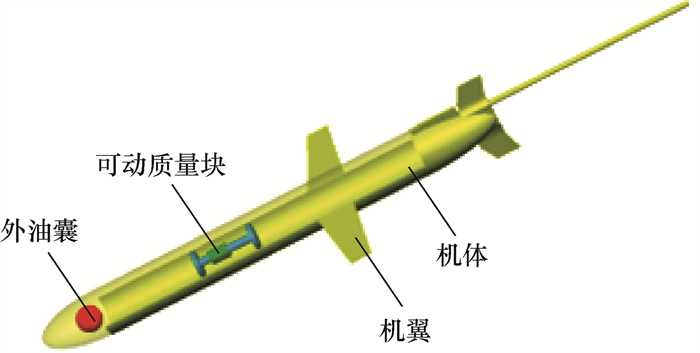
|
| 图 1 水下滑翔机结构示意图 |
机体外形为Myring线型的回转体,广泛应用于各类水下航行器。机翼的基本外形为等厚度梯形,可产生较大升力,关键参数如表 1所示。外油囊位于机体前端,与外部流体介质连通,通过控制注油量改变其体积,实现整机净浮力调节。
已有研究表明,翼面沟槽可有效降低水下滑翔机阻力,有望提升水下滑翔机综合性能[21-23]。沟槽结构的设计思路来源于鲨鱼表皮的齿结构[24-26],能有效抑制和延迟紊流的发生。实际工程中,上述齿结构难以大规模生产,常将其简化为“V”形、梯形、矩形、圆形等槽结构。对应的截面形状如图 2所示。其中“V”形沟槽在水下滑翔机应用中的减阻效果已得到证实,因此本文重点以该形沟槽为研究对象。
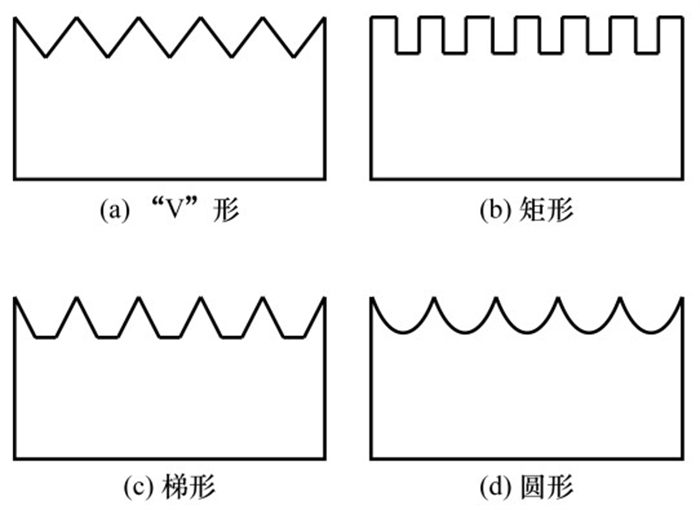
|
| 图 2 4种常见沟槽的截面 |
本文假设水下滑翔机机翼上下表面均存在沟槽形貌,沟槽的关键参数包括沟槽间距s、沟槽深度h、沟槽方向角β,具体几何含义如图 3所示。当β=0°时,沟槽方向与机体长轴平行。
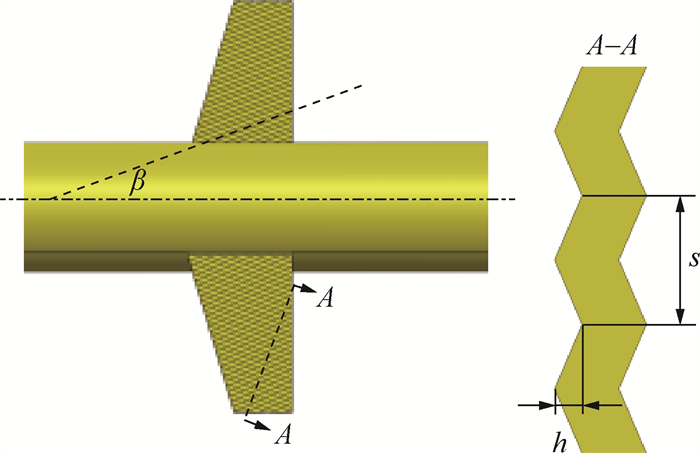
|
| 图 3 沟槽参数几何含义 |
后续优化设计中,选取s、h、β作为设计对象,取值范围如表 2所示。
2 水下滑翔机性能分析模型 2.1 CFD模型
在大部分探测任务中,水下滑翔机的整个运动过程可分为多轮剖面内滑翔运动;每一轮剖面内滑翔运动称为单剖面滑翔运动。对于该运动形式,水下滑翔机的运动轨迹在理论上始终位于一个竖直平面内,且航行速度稳定[27]。
水下滑翔机稳态运动过程中,所受外力主要包括浮力、重力和水动力。浮力和重力可根据水下滑翔机的自身性质进行求解,水动力在本文中基于CFD方法确定。首先,采用SOLIDWORKS软件建立圆柱水池和水下滑翔机的三维模型,通过Boole运算构建流域模型,如图 4所示。其中,水下滑翔机机体表面设为静止无滑移壁面边界,水池壁面设为自由滑移壁面。模型右侧设为流体入口,左侧为出口。通过旋转水下滑翔机,可开展不同攻角α下的稳态运动CFD仿真。
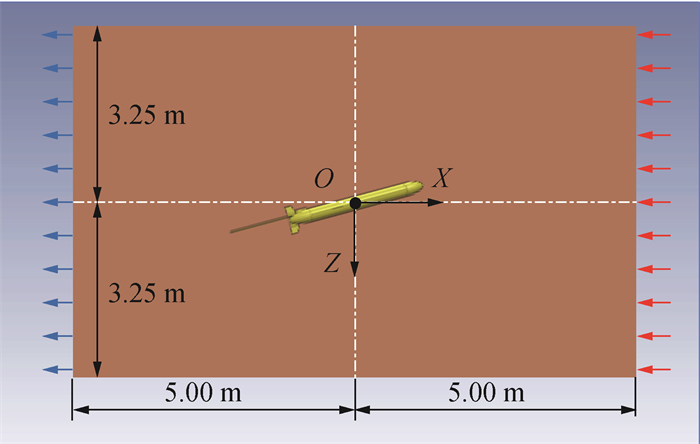
|
| 图 4 流域模型 |
采用Workbench Meshing软件的非结构化网格自动划分技术对三维模型进行网格划分。为提高仿真精度,对部分区域网格进行细化。经网格无关性验证,网格划分方案为:流域模型中网格单元尺寸为100 mm,水下滑翔机机体表面网格单元尺寸为6 mm,机翼表面网格单元尺寸为4 mm,模型网格总数约一千万个,如图 5所示。

|
| 图 5 CFD模型网格划分 |
采用FLUENT软件开展CFD仿真分析,基于有限体积法求解Navier-Stokes方程,利用SST k-ω湍流模型开展仿真计算,该模型的壁面增强函数可进一步提高计算精度。将流域中的介质视为不可压缩粘性流体,密度设为1 020 kg/m3,动力黏度设为1.024×10-4 kg/(m·s)。水池的入口、出口分别设为速度入口边界、压力出口边界,入口边界的速度设为0.2 m/s,出口边界的压力为1.013×105 Pa。选择SIMPLE算法求解压力场和速度场,数值离散采用二阶迎风格式。为保证计算收敛精度,将连续性和速度分量的收敛标准设为10-6,数值迭代步数设为3 000步。
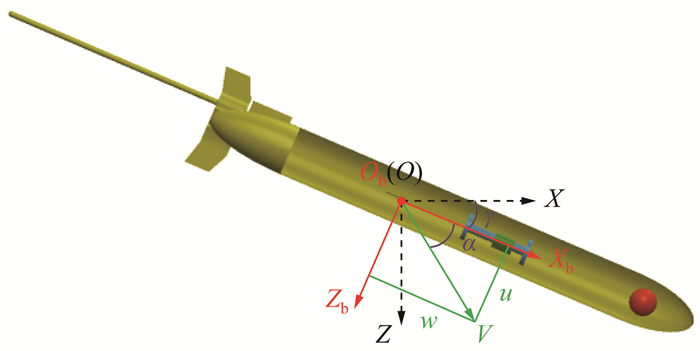
为方便后续研究,建立图 6所示的直角坐标系。X轴、Y轴和Z轴组成惯性坐标系,原点为O,X轴和Y轴位于水平面内,Z轴指向与重力方向一致;Xb轴、Yb轴和Zb轴组成水下滑翔机随体坐标系,原点为净浮力为0时的整机浮心Ob,Xb轴指向水下滑翔机头部,Zb轴指向水下滑翔机底部。2个坐标系均满足右手定则。其中:α表示攻角,γ表示俯仰角,V表示水下滑翔机速度。CFD仿真过程中,水下滑翔机位置固定不变,流体的流速可视为水下滑翔机速度,且α的取值范围设为[—5°, 5°]。将 V在Xb轴和Zb轴的分量表示为u和w,则α可表示为
| $ \alpha=\arctan \frac{w}{u} . $ | (1) |
|
| 图 6 水下滑翔机坐标系 |
稳态滑翔过程中 V为定值,此时水下滑翔机受到的水动力为黏性水动力。根据文[28],作用于Ob处的黏性水动力Fs及其附加力矩 Ms在随体坐标系下可表示为
| $ F_{{\mathrm{s}}}=\|\boldsymbol{V}\|_2^2\left[\begin{array}{c} -D \cos \alpha+L \sin \alpha \\ 0 \\ -D \sin \alpha-L \cos \alpha \end{array}\right] , $ | (2) |
| $ {\boldsymbol{M}}_{{\mathrm{s}}}=\|\boldsymbol{V}\|_2^2\left[\begin{array}{c} 0 \\ M \\ 0 \end{array}\right] . $ | (3) |
其中:D、L和M分别表示速度归一化的阻力、升力和俯仰力矩,单位分别为kg/m, kg/m和kg, 均为α、s、h和β的函数。
CFD仿真的目的是确定含翼面沟槽水下滑翔机的黏性水动力方程,因此需要在不同翼面沟槽参数和α条件下开展CFD仿真计算。采用优化拉丁超立方试验设计,结合表 2中的翼面沟槽参数和α的取值范围抽取符合要求的60组样本点,分别代入CFD模型开展仿真计算。基于仿真结果,采用二阶多项式拟合L、D和M的近似表达式。
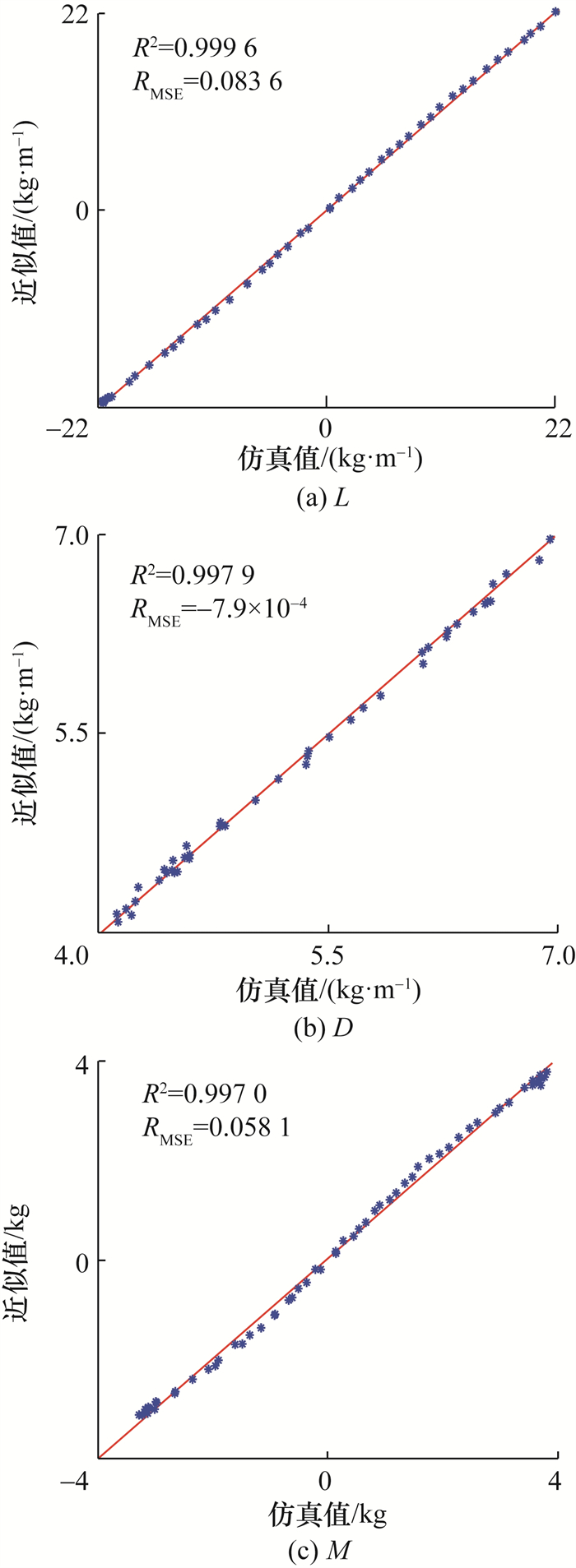
采用文[9]所述的决定系数R2和均方根相对误差RMSE验证水动力方程拟合精度。R2越接近1,RMSE越接近0,则拟合精度越高。评估结果如图 7所示,以CFD仿真结果为横坐标,以多项式近似结果为纵坐标,由图可知,R2非常接近于1,RMSE非常接近于0,散点均靠近1∶1线,说明水动力方程拟合精度较高,能准确反映水下滑翔机的水动力特性。
|
| 图 7 水动力方程拟合精度评估(L、D、M已经过速度归一化处理) |
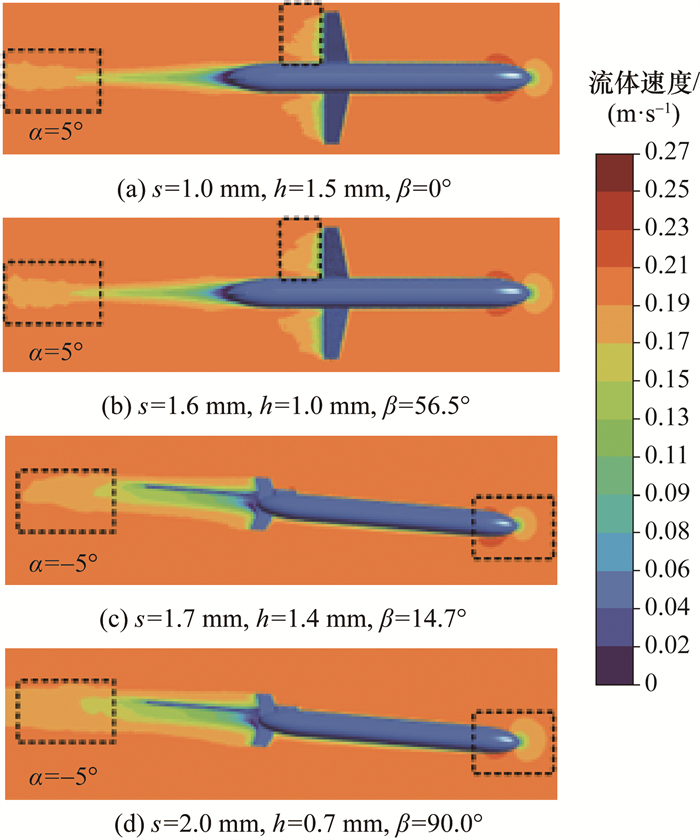
为了更加直观地展现CFD仿真结果,进一步给出4组不同仿真工况下的速度云图,如图 8所示。由图可知,α相同而翼面沟槽参数不同时,水下滑翔机头部、机翼、尾部附近的流体速度具有明显差异,说明翼面沟槽对水下滑翔机水动力性能具有一定影响。
|
| 图 8 CFD仿真结果对比 |
2.2 性能指标分析
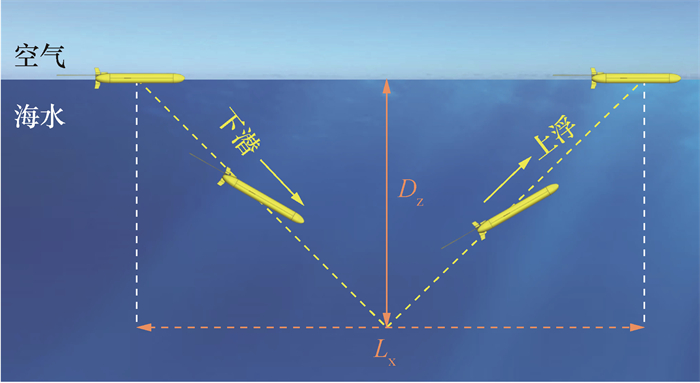
本文重点关注水下滑翔机在执行单剖面滑翔运动时的性能,根据文[9-10],航速直接影响运动效率和精度,静稳定性直接决定运行可靠性,能耗直接关系水下滑翔机续航能力。单剖面滑翔运动过程如图 9所示,首先水下滑翔机漂浮在水面上,接收控制指令;收到指令后的水下滑翔机进行净浮力调节量c1和可动质量块平移量c2的调整,并开始下潜;当下潜到目标深度Dz后,水下滑翔机再次调节c1和c2,并开始上浮,最终再次浮出水面。其中,Lx表示单剖面滑翔运动航程。
|
| 图 9 单剖面滑翔运动示意图 |
为开展水下滑翔机性能分析,需建立其动力学模型。为此,设可动质量块的质心相对于随体坐标系原点Ob的位置向量为 rp,外油囊浮心相对于Ob的位置向量为 re,水下滑翔机(不包含可动质量块)的质心相对于Ob的位置向量为 rh,水下滑翔机(不包含可动质量块)质量为mb,可动质量块质量为mp,水下滑翔机的特征长度为l。对于“海燕-Ⅱ”型水下滑翔机,rp、re和 rh满足如下关系:
| $ \left\{\begin{array}{l} \boldsymbol{r}_{{\mathrm{p}}}=\left[\begin{array}{llll} l_{{\mathrm{p}} 0}+c_2 & 0 & e \end{array}\right]^{{\mathrm{T}}}, \\ \boldsymbol{r}_{{\mathrm{e}}}=\left[\begin{array}{lll} l_{{\mathrm{e}}} & 0 & 0 \end{array}\right]^{{\mathrm{T}}}, \\ \boldsymbol{r}_{{\mathrm{h}}}=\left[\begin{array}{llll} l_{{\mathrm{hx}}} & 0 & l_{{\mathrm{h}} {\mathrm{x}}} \end{array}\right]^{{\mathrm{T}}} . \end{array}\right. $ | (4) |
其中lp0、e、le、lhx、lhz表示与水下滑翔机构型相关的常数,具体数值如表 3所示。
| 参数 | 取值 | 参数 | 取值 |
| l/mm | 221 | lhx/mm | -27 |
| lp0/mm | 90 | lhz/mm | 20 |
| e/mm | 16 | mb/kg | 54.5 |
| le/mm | 840 | mp/kg | 16.4 |
根据Wu等[28]的研究,建立水下滑翔机稳态运动的动力学方程如下:
| $ \left\{\begin{array}{l} -c_1 \sin \gamma=\|\boldsymbol{V}\|_2^2(D \cos \alpha-L \sin \alpha), \\ c_1 \cos \gamma=\|\boldsymbol{V}\|_2^2(D \sin \alpha+L \cos \alpha), \\ \left(l_{{\mathrm{e}}} c_1+c_2 m_{{\mathrm{p}}} g\right) \cos \gamma+ \\ \left(e m_{{\mathrm{p}}} g+l_{{\mathrm{hz}} } m_{{\mathrm{b}}} g\right) \sin \gamma=\|\boldsymbol{V}\|_2^2 M . \end{array}\right. $ | (5) |
其中:g表示重力加速度,取9.8 m/s2。为了方便后续推导,这里规定控制参数c1和c2的取值范围分别为[2.5, 5.0] N和[0.01, 0.04] m。当水下滑翔机做下潜运动时,c1和c2的取值均大于0。与文[12]一致,当水下滑翔机做上浮运动时,控制参数值变为-c1和-c2。当翼面沟槽参数s、h和β,以及水下滑翔机控制参数c1、c2取值确定后,式(5)中的未知数仅剩‖ V ‖2、γ和α,本文采用MATLAB软件中vpasolve函数求解该非线性方程组。
设水下滑翔机稳态运动的水平速度和竖直速度分别为vx和vz,根据几何关系则有
| $ \left\{\begin{array}{l} v_{{\mathrm{x}}}=\|\boldsymbol{V}\|_2 \cos (\alpha+\gamma), \\ v_{{\mathrm{z}}}=\|\boldsymbol{V}\|_2 \sin (\alpha+\gamma) . \end{array}\right. $ | (6) |
水下滑翔机的下潜运动时间tf和上浮运动时间tr分别为
| $ \left\{\begin{array}{l} t_{{\mathrm{f}}}=\left|\frac{D_{{\mathrm{z}}}}{v_{{\mathrm{fz}}}}\right|, \\ t_{{\mathrm{r}}}=\left|\frac{D_{{\mathrm{z}}}}{v_{{\mathrm{rz}}}}\right|. \end{array}\right. $ | (7) |
其中:vfz表示稳态下潜竖直速度,vrz表示稳态上浮竖直速度。因此,Lx可表示为
| $ L_{{\mathrm{x}}}=t_{{\mathrm{f}}} \mathcal{v}_{{\mathrm{fx}}}+t_{{\mathrm{r}}} \mathcal{v}_{{\mathrm{rx}}}. $ | (8) |
其中:vfx表示稳态下潜水平速度,vrx表示稳态上浮水平速度。进一步,可得水下滑翔机的平均水平速度vx-ave和平均竖直速度vz-ave,如式(9)所示。
| $ \left\{\begin{array}{l} v_{{\mathrm{x}} \text {-ave }}=\frac{L_{{\mathrm{x}}}}{t_{{\mathrm{f}}}+t_{{\mathrm{r}}}}, \\ v_{{\rm{z}} \text {-ave }}=\frac{2 D_{\rm{z}}}{t_{{\mathrm{f}}}+t_{{\mathrm{r}}}} . \end{array}\right. $ | (9) |
静稳定性是水下滑翔机的重要性能之一,本文采用无因次水动力中心臂l′作为水下滑翔机静稳定性评判指标[29],l′值越小,水下滑翔机静稳定性越高,其表达式如下:
| $ l^{\prime}=-\frac{M}{L l} . $ | (10) |
考虑水下滑翔机下潜和上浮时的l′可能存在差异,进一步定义平均无因次水动力中心臂l′ave,其表达式如下:
| $ l_{\text {ave }}^{\prime}=\frac{l_{{\mathrm{f}}}^{\prime}+l_{{\mathrm{r}}}^{\prime}}{2} . $ | (11) |
其中l′f和l′r分别表示水下滑翔机下潜和上浮运动时的无因次水动力中心臂。
单剖面滑翔运动中,水下滑翔机将进行3次浮力调节与姿态调节。其中,浮力调节系统中的电磁阀和液压泵会控制外油囊中的油量,姿态调节系统驱动可动质量块前后移动。控制系统在水下滑翔机运动过程中持续工作,测量系统包含持续和间断开启的2种传感器。单剖面滑翔运动中,水下滑翔机能耗来自于以上4个系统。
浮力调节系统中,设电磁阀的功率和流量分别为pv和qv,液压泵的功率和流量分别为pb和qb。根据文[12],浮力调节系统的能耗可表示为
| $ E_1=\frac{2 c_1}{\rho g}\left(\frac{p_{{\mathrm{b}}}}{q_{{\mathrm{b}}}}+\frac{p_{{\mathrm{v}}}}{q_{{\mathrm{v}}}}\right) . $ | (12) |
姿态调节系统中,设可动质量块的平移速度为vm、驱动功率为pm,且pm与γ密切相关, pm(γ)=1.43+0.067|γ|。当水下滑翔机准备下潜时,γ可视为0,下潜和上浮运动过程中的γ均视为常数,分别表示为γf和γr。根据文[11-12],姿态调节系统的能耗表示为
| $ E_2=\frac{c_2}{v_{{\mathrm{m}}}} p_{{\mathrm{m}}}(0)+\frac{2 c_2}{v_{{\mathrm{m}}}} p_{{\mathrm{m}}}\left(\gamma_{{\mathrm{f}}}\right)+\frac{c_2}{v_{{\mathrm{m}}}} p_{{\mathrm{m}}}\left(\gamma_{{\mathrm{r}}}\right) . $ | (13) |
设控制系统平均功率为pc,对应的能耗表示为
| $ E_3=\left(t_{{\mathrm{f}}}+t_{{\mathrm{r}}}\right) p_{{\mathrm{c}}} . $ | (14) |
测量系统中,设持续开启型传感器的平均功率为pcs;间断开启型传感器每隔一定下潜深度Δd开启一次,设单次开启时间为Δt、平均功率为pis。因此,测量系统的能耗表示为
| $ \begin{gathered} E_4=\left(t_{{\mathrm{f}}}+t_{{\mathrm{r}}}\right) p_{{\mathrm{cs}}}+ \\ \left(\frac{D_{\rm{z}} \Delta t}{\Delta t\left|v_{{\mathrm{fz}}}\right|+\Delta d}+\frac{D_{\rm{z}} \Delta t}{\Delta t\left|v_{{\mathrm{rz}}}\right|+\Delta d}\right) p_{{\mathrm{is}}} . \end{gathered} $ | (15) |
基于上述分析,确定水下滑翔机的总能耗为
| $ E=E_1+E_2+E_3+E_4 . $ | (16) |
进一步定义比能耗Save,其物理意义为消耗单位能量所能获得的有效航程,Save越大,水下滑翔机能量利用率越高。其表达式如下:
| $ S_{{\mathrm{ave}}}=\frac{L_{{\mathrm{x}}}}{E} . $ | (17) |
为获得最佳翼面沟槽设计方案,需要以翼面沟槽参数为设计变量,开展水下滑翔机综合性能优化。除翼面沟槽参数外,水下滑翔机性能还与控制参数c1和c2、目标下潜深度Dz密切相关。在本研究中,将Dz设定为400 m。在此基础上,本文优化目标是使水下滑翔机具备较高的水平航速、垂直航速, 优化比能耗以及静稳定性。
开展优化迭代计算前,需建立c1、c2、s、h、β和vx-ave、vz-ave、l′ave、Save之间的映射关系。
| $ \left\{\begin{array}{l} v_{\text {x-ave }}=f_1\left(c_1, c_2, s, h, \beta\right), \\ v_{ \text {z-ave }}=f_2\left(c_1, c_2, s, h, \beta\right), \\ l_{\text {ave }}^{\prime}=f_3\left(c_1, c_2, s, h, \beta\right), \\ S_{\text {ave }}=f_4\left(c_1, c_2, s, h, \beta\right) . \end{array}\right. $ | (18) |
其中f1、f2、f3和f4表示映射函数,可能是显函数或隐函数。由于后续优化设计变量仅为s、h和β,为充分考虑c1、c2的影响,对式(18)进行多元积分,最终得到式(19)。
| $ \left\{\begin{array}{l} v_{\text {x-int }}=\frac{\int_{c_2^{{\mathrm{L}}}}^{c_2^{{\mathrm{R}}}} \int_{c_1^{{\mathrm{L}}}}^{c_1^{{\mathrm{R}}}} f_1\left(c_1, c_2, s, h, \beta\right) {\mathrm{d}} c_1 {\mathrm{~d}} c_2}{\left(c_2^{{\mathrm{R}}}-c_2^{{\mathrm{L}}}\right)\left(c_1^{{\mathrm{R}}}-c_1^{{\mathrm{L}}}\right)}, \\ v_{\text {z-int }}=\frac{\int_{c_2^{{\mathrm{L}}}}^{c_2^{{\mathrm{R}}}} \int_{c_1^{{\mathrm{L}}}}^{c_1^{{\mathrm{R}}}} f_2\left(c_1, c_2, s, h, \beta\right) {\mathrm{d}} c_1 {\mathrm{~d}} c_2}{\left(c_2^{{\mathrm{R}}}-c_2^{{\mathrm{L}}}\right)\left(c_1^{{\mathrm{R}}}-c_1^{{\mathrm{L}}}\right)}, \\ l_{\text {int }}^{\prime}=\frac{\int_{c_2^{{\mathrm{L}}}}^{c_2^{{\mathrm{R}}}} \int_{c_1^{{\mathrm{L}}}}^{c_1^{{\mathrm{R}}}} f_3\left(c_1, c_2, s, h, \beta\right) {\mathrm{d}} c_1 {\mathrm{~d}} c_2}{\left(c_2^{{\mathrm{R}}}-c_2^{{\mathrm{L}}}\right)\left(c_1^{{\mathrm{R}}}-c_1^{{\mathrm{L}}}\right)}, \\ S_{\text {int }}=\frac{\int_{c_2^{{\mathrm{L}}}}^{c_2^{{\mathrm{R}}}} \int_{c_1^{{\mathrm{L}}}}^{c_1^{{\mathrm{R}}}} f_4\left(c_1, c_2, s, h, \beta\right) {\mathrm{d}} c_1 {\mathrm{~d}} c_2}{\left(c_2^{{\mathrm{R}}}-c_2^{{\mathrm{L}}}\right)\left(c_1^{{\mathrm{R}}}-c_1^{{\mathrm{L}}}\right)} . \end{array}\right. $ | (19) |
其中:vx-int、vz-int、l′int和Sint表示c1、c2影响下的水下滑翔机平均性能指标,c1L、c2L分别表示c1、c2的下界,c1R、c2R分别表示c1、c2的上界。
实际上,求解式(18)需要采用数值方法开展迭代计算,会消耗一定计算时间。此外,采用求解非线性方程的方式分析水下滑翔机性能时,较难开展式(19)所示的积分运算,甚至需要借助Monte Carlo法求解性能评估参数值,这将消耗大量计算时间,不利于开展优化迭代计算。因此有必要获取f1、f2、f3和f4的显式表达形式。为此,本文通过优化拉丁超立方试验设计,在c1、c2、s、h和β取值范围内抽取100组样本点,然后将84组样本点代入式(5)—(17)中,开展动力学仿真与性能评估,得到对应的100组vx-ave、vz-ave、l′ave和Save。最后,利用二阶多项式对所得数据进行最小二乘拟合,得到性能评估模型的代理模型。
本节同样采用R2和RMSE验证性能评估代理模型的拟合精度,结果如图 10所示,以动力学仿真结果为横坐标,以代理模型近似结果为纵坐标。由图可知,R2均非常接近于1,RMSE均非常接近于0,散点均靠近1∶1线,说明代理模型拟合精度较高,能准确输入与输出之间的映射关系。
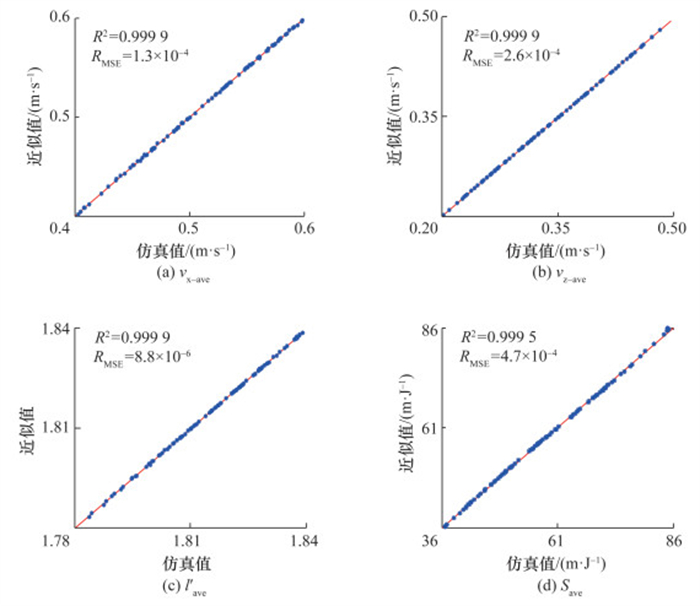
|
| 图 10 代理模型拟合性能指标的精度评估 |
利用式(19)对所得代理模型进行多元积分,得到含翼面沟槽的水下滑翔机性能评估参数的近似表达式如下:
| $ \left\{\begin{aligned} v_{\text { x-int }} \approx & -9.80 \times 10^{-7} \beta^2-1.73 \times 10^{-4} \beta h+2.70 \times 10^{-5} \beta s+1.29 \times 10^{-4} \beta-1.23 \times 10^{-2} h^2+ \\ & 3.98 \times 10^{-3} h s+3.46 \times 10^{-2} h-6.97 \times 10^{-3} s^2+1.44 \times 10^{-2} s+0.494, \\ v_{ \text {y-int }} \approx & -4.58 \times 10^{-7} \beta^2-1.15 \times 10^{-4} \beta h+2.27 \times 10^{-5} \beta s+7.46 \times 10^{-5} \beta-6.93 \times 10^{-4} h^2+ \\ & 2.08 \times 10^{-3} h s+2.03 \times 10^{-2} h-3.93 \times 10^{-3} s^2+7.95 \times 10^{-3} s+0.315, \\ l_{\text {int }}^{\prime} \approx & 8.09 \times 10^{-8} \beta^2+6.15 \times 10^{-5} \beta h-1.93 \times 10^{-5} \beta s-1.81 \times 10^{-5} \beta+2.23 \times 10^{-3} h^2- \\ & 1.33 \times 10^{-3} h s-4.98 \times 10^{-3} h+1.61 \times 10^{-3} s^2-2.75 \times 10^{-3} s+1.82, \\ S_{\text {int }} \approx & -4.82 \times 10^{-5} \beta^2-7.16 \times 10^{-3} \beta h-4.29 \times 10^{-4} \beta s+8.28 \times 10^{-3} \beta-0.248 h^2+ \\ & 0.207 h s+0.748 h-0.525 s^2+1.31 s+56.665 . \end{aligned}\right. $ | (20) |
基于式(20)绘制vx-int、vz-int、l′int和Sint的近似函数图像,如图 11所示。结果表明,β取值越小、h取值越大,水下滑翔机各项性能越优异。因此,可直接确定β和h的最优解分别为0°和1.5 mm。但s对水下滑翔机各项性能指标的影响存在一定矛盾关系,无法直接确定其最优取值。
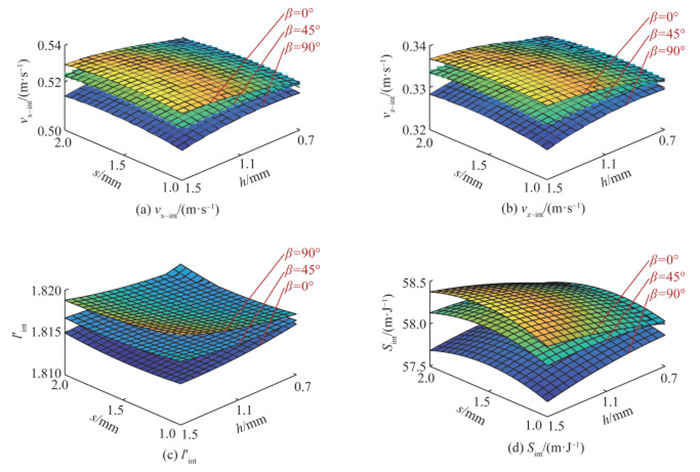
|
| 图 11 翼面沟槽参数与性能的关系图 |
3 翼面沟槽参数多目标优化 3.1 优化数学模型
性能评估模型表明,考虑不同s取值时,vx-int、vz-int、l′int、Sint之间存在一定矛盾关系,因此有必要采用多目标优化算法确定最佳翼面沟槽参数。根据前文内容,建立优化数学模型如下:
| $ \left\{\begin{array}{l} \max \left(v_{{\mathrm{x}}-{\mathrm{int}}}, v_{{\mathrm{z-int}}}, S_{{\mathrm{int}}}\right) \\ \min l_{{\mathrm{int}}}^{\prime} \\ \text { s. t. } s^{{\mathrm{L}}} \leqslant s \leqslant s^{{\mathrm{R}}} \end{array} .\right. $ | (21) |
其中sL和sR分别表示s的下界和上界。
对于式(21)所示的多目标优化数学模型,本文采用第二代非劣排序遗传算法(NSGA-Ⅱ)对其进行求解。NSGA-Ⅱ引入精英策略和快速非支配排序算法,具有运行速度快,解集收敛性好的优点,在处理多目标优化问题时具有显著的优势。优化计算过程中,NSGA-Ⅱ的参数配置如表 4所示。
3.2 优化结果及验证
优化计算完成后,得到由198组非劣解组成的Pareto最优解集。从Pareto最优解集中选取5组解:其中4组解分别对应最大vx-int、最大vz-int、最小l′int和最大Sint;另一组为使水下滑翔机平均性能最优的折中解,如表 5所示。由表可知,最大水平航速、垂直航速、比能耗以及最优的静稳定性对应的沟槽参数均存在一定的差别。
| 编号 | s/mm | vx-int/(m·s-1) | vz-int/(m·s-1) | l′int | Sint/(m·J-1) |
| 1 | 1.46 | 0.533 | — | — | — |
| 2 | 1.41 | — | 0.338 2 | — | — |
| 3 | 1.48 | — | — | 1.814 4 | — |
| 4 | 1.55 | — | — | — | 58.497 |
| 5 | 1.50 | 0.533 | 0.338 1 | 1.814 4 | 58.482 |
利用第2章所述方法分析不含翼面沟槽的水下滑翔机性能,结果如表 6所示。结合表 5和表 6数据可知,带有特殊翼面沟槽的水下滑翔机比不含翼面沟槽的单一性能和综合性能更优,这表明翼面沟槽的存在可有效提升水下滑翔机综合性能,此结论可为实际水下滑翔机设计提供理论指导。
| 性能指标 | vx-int/(m·s-1) | vz-int/(m·s-1) | l′int | Sint/(m·J-1) |
| 取值 | 0.502 | 0.307 0 | 1.847 8 | 55.551 |
为验证设计方法的工程可行性,采用3D打印技术试制机翼样机。由于制造难度随s的减小而增大,故从表 6中选取s最小的机翼构型(s=1.41 mm)作为制造对象,以充分验证可行性,结果如图 12所示。由图可知,机翼样机表面光滑,沟槽轮廓清晰、无变形,这表明了含翼面沟槽的机翼具有可制造性,进一步证明本研究工作的合理性。
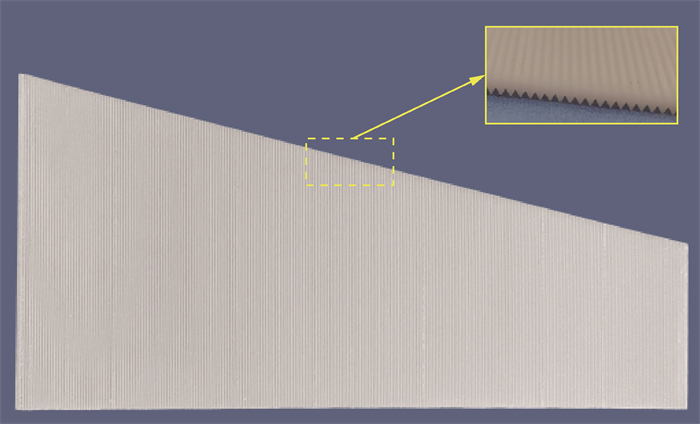
|
| 图 12 机翼样机图(s=1.41 mm) |
4 结论
本文结合CFD仿真、动力学分析、代理模型技术和多目标优化算法,开展了水下滑翔机翼面沟槽参数的多目标设计优化,以提升水下滑翔机综合性能。得到以下主要结论:
1) 较小的沟槽方向角和较大的沟槽深度可有效提升水下滑翔机航速和静稳定性、降低能耗,沟槽间距对水下滑翔机各项性能指标的影响存在一定矛盾关系。
2) 沟槽间距与水下滑翔机各项性能指标之间的函数关系呈非单调性,需借助优化计算确定其最优值。
3) 优化结果表明,对应最快航速、最优静稳定性和最低能耗的沟槽间距取值不同。与不含翼面沟槽水下滑翔机性能分析结果对比表明,翼面沟槽可有效提升水下滑翔机综合性能。
4) 采用3D打印技术可制造含翼面沟槽的机翼样机,证明了设计方法的工程可行性。
| [1] |
STOMMEL H. The Slocum mission[J]. Oceanography, 1989, 2(1): 22-25. DOI:10.5670/oceanog.1989.26 |
| [2] |
WEBB D C, SIMONETTI P J, JONES C P. SLOCUM: An underwater glider propelled by environmental energy[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 447-452. DOI:10.1109/48.972077 |
| [3] |
ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seaglider: A long-range autonomous underwater vehicle for oceanographic research[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 424-436. DOI:10.1109/48.972073 |
| [4] |
SHERMAN J, DAVIS R E, OWENS W B, et al. The autonomous underwater glider "Spray"[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 437-446. DOI:10.1109/48.972076 |
| [5] |
YU J C, ZHANG A Q, JIN W M, et al. Development and experiments of the Sea-Wing underwater glider[J]. China Ocean Engineering, 2011, 25(4): 721-736. DOI:10.1007/s13344-011-0058-x |
| [6] |
WANG S X, SUN X J, WANG Y H, et al. Dynamic modeling and motion simulation for a winged hybrid-driven underwater glider[J]. China Ocean Engineering, 2011, 25(1): 97-112. DOI:10.1007/s13344-011-0008-7 |
| [7] |
JAVAID M Y, OVINIS M, HASHIM F B M, et al. Effect of wing form on the hydrodynamic characteristics and dynamic stability of an underwater glider[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(4): 382-389. DOI:10.1016/j.ijnaoe.2016.09.010 |
| [8] |
李靖璐, 王鹏, 牛宏磊, 等. 自由变形在水翼外形优化设计中的应用[J]. 哈尔滨工程大学学报, 2020, 41(9): 1249-1254. LI J L, WANG P, NIU H L, et al. Application of free-form deformation method in the shape optimization design of hydrofoil[J]. Journal of Harbin Engineering University, 2020, 41(9): 1249-1254. (in Chinese) |
| [9] |
WU Q J, WU H Y, JIANG Z H, et al. Multi-objective optimization and driving mechanism design for controllable wings of underwater gliders[J]. Ocean Engineering, 2023, 286: 115534. DOI:10.1016/j.oceaneng.2023.115534 |
| [10] |
杨明. 长航程水下滑翔机系统设计及关键参数优化研究[D]. 天津: 天津大学, 2021. YANG M. System design and key parameter optimization of a long-voyage underwater glider[D]. Tianjin: Tianjin University, 2021. (in Chinese) |
| [11] |
WU H Y, NIU W D, ZHANG Y L, et al. A hybrid polynomial-based optimization method for underwater gliders with parameter uncertainty[J]. Tianjin: Applied Ocean Research, 2023, 133: 103486. DOI:10.1016/j.apor.2023.103486 |
| [12] |
SONG Y, WANG Y H, YANG S Q, et al. Sensitivity analysis and parameter optimization of energy consumption for underwater gliders[J]. Energy, 2020, 191: 116506. DOI:10.1016/j.energy.2019.116506 |
| [13] |
吴青建, 吴宏宇, 江智宏, 等. 面向水下定点探测的水下滑翔机控制参数优化[J]. 清华大学学报(自然科学版), 2023, 63(1): 62-70. WU Q J, WU H Y, JIANG Z H, et al. Control parameter optimization of underwater gliders for underwater fixed-point exploration missions[J]. Journal of Tsinghua University (Science and Technology), 2023, 63(1): 62-70. (in Chinese) |
| [14] |
吴宏宇, 牛文栋, 宋扬, 等. 受最速降线启发的水下滑翔机运动轨迹设计[J/OL]. 机械工程学报: 1-11[2024-03-17]. http://kns.cnki.net/kcms/detail/11.2187.TH.20231005.1818.012.html. WU H Y, NIU W D, SONG Y, et al. Motion trajectory design for underwater gliders inspired by brachistochrone[J/OL]. Journal of Mechanical Engineering: 1-11[2024-03-17]. http://kns.cnki.net/kcms/detail/11.2187.TH.20231005.1818.012.html. (in Chinese) |
| [15] |
FU X Y, LEI L, YANG G, et al. Multi-objective shape optimization of autonomous underwater glider based on fast elitist non-dominated sorting genetic algorithm[J]. Ocean Engineering, 2018, 157: 339-349. DOI:10.1016/j.oceaneng.2018.03.055 |
| [16] |
YANG M, WANG Y H, YANG S Q, et al. Shape optimization of underwater glider based on approximate model technology[J]. Applied Ocean Research, 2021, 110: 102580. DOI:10.1016/j.apor.2021.102580 |
| [17] |
姜均喆. 水下滑翔机总体设计与水动力性能分析[D]. 上海: 上海交通大学, 2018. JIANG J Z. Design and hydrodynamic analysis of underwater glider[D]. Shanghai: Shanghai Jiao Tong University, 2018. (in Chinese) |
| [18] |
胡海豹, 宋保维, 潘光, 等. 回转体表面条纹沟槽减阻水洞实验研究[J]. 力学季刊, 2006, 27(2): 267-272. HU H B, SONG B W, PAN G, et al. Water tunnel experimental investigation on drag reduction in gyroidal objects with riblets surface[J]. Chinese Quarterly of Mechanics, 2006, 27(2): 267-272. DOI:10.3969/j.issn.0254-0053.2006.02.014 (in Chinese) |
| [19] |
杨海霞. 沟槽面湍流边界层减阻的数值研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. YANG H X. Numerical study of turbulent drag reduction over riblet surface[D]. Harbin: Harbin Engineering University, 2008. (in Chinese) |
| [20] |
王晋军, 兰世隆, 苗福友. 沟槽面湍流边界层减阻特性研究[J]. 中国造船, 2001, 42(4): 1-5. WANG J J, LAN S L, MIAO F Y. Drag-reduction characteristics of turbulent boundary layer flow over riblets surfaces[J]. Ship Building of China, 2001, 42(4): 1-5. DOI:10.3969/j.issn.1000-4882.2001.04.001 (in Chinese) |
| [21] |
张帅. 长航程水下滑翔机的减阻技术研究[D]. 天津: 天津大学, 2018. ZHANG S. Study on drag reduction technology of Long-voyage underwater glider[D]. Tianjin: Tianjin University, 2018. (in Chinese) |
| [22] |
BECHERT D W, BRUSE M, HAGE W, et al. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry[J]. Journal of Fluid Mechanics, 1997, 338: 59-87. DOI:10.1017/S0022112096004673 |
| [23] |
PARK S R, WALLACE J M. Flow alteration and drag reduction by riblets in a turbulent boundary layer[J]. AIAA Journal, 1994, 32(1): 31-38. DOI:10.2514/3.11947 |
| [24] |
BIXLER G D, BHUSHAN B. Fluid drag reduction with shark-skin riblet inspired microstructured surfaces[J]. Advanced Functional Materials, 2013, 23(36): 4507-4528. DOI:10.1002/adfm.201203683 |
| [25] |
BECHERT D, REIF W. On the drag reduction of the shark skin[C]//23rd Aerospace Sciences Meeting. Reno, USA: American Institute of Aeronautics and Astronautics, 1985.
|
| [26] |
刘宝胜, 吴为, 曾元松. 鲨鱼皮仿生结构应用及制造技术综述[J]. 塑性工程学报, 2014, 21(4): 56-62. LIU B S, WU W, ZENG Y S. Review on application and fabrication of shark skin bionic structure[J]. Journal of Plasticity Engineering, 2014, 21(4): 56-62. DOI:10.3969/j.issn.1007-2012.2014.04.012 (in Chinese) |
| [27] |
刁宏伟, 李宗吉, 王世哲, 等. 水下滑翔机研究现状及发展趋势[J]. 舰船科学技术, 2022, 44(6): 8-12. DIAO H W, LI Z J, WANG S Z, et al. The research status and development trend of underwater glider[J]. Ship Science and Technology, 2022, 44(6): 8-12. DOI:10.3404/j.issn.1672-7649.2022.06.002 (in Chinese) |
| [28] |
WU H Y, NIU W D, ZHANG Y L, et al. Multidisciplinary optimization-based path planning for underwater gliders executing multi-point exploration missions[J]. Ocean Engineering, 2022, 266: 113022. DOI:10.1016/j.oceaneng.2022.113022 |
| [29] |
武建国, 陈超英, 王树新, 等. 混合驱动水下滑翔器滑翔状态机翼水动力特性[J]. 天津大学学报, 2010, 43(1): 84-89. WU J G, CHEN C Y, WANG S X, et al. Hydrodynamic characteristics of the wings of hybrid-driven underwater glider in glide mode[J]. Journal of Tianjin University, 2010, 43(1): 84-89. (in Chinese) |



