离心泵广泛应用于清洁能源、先进动力和国防安全等领域。随着系统调节需求的增加，离心泵在设计工况点和一定区间的非设计工况点均需实现高效运行，因此亟需发展相应的设计方法。离心泵一元理论设计方法假定轴面速度沿叶轮过水断面均匀分布，主要包括模型相似法和速度系数法。二元理论设计方法假定轴面速度为有势流动或给定的某种有旋流动。吴仲华^[1]于1952年提出了基于两类相对流面的三元流动理论，自此三元理论设计方法开始蓬勃发展，例如Borges^[2]提出了全三维反问题设计方法并将其应用于水轮机设计，Zangeneh等^[3-5]提出了适用于可压缩流体的径流式和混流式叶轮机械全三维设计方法，Goto等^[6]在此基础上开发了包括三维几何建模、网格生成和流动数值模拟的水泵设计平台。

叶片载荷是旋转叶轮做功的核心参数，决定了叶轮做功的能力和效率。在三维反问题设计中，给定叶片载荷分布，结合轴面流场计算结果，可得到叶片三维几何形状。曹树良等^[7]提出了基于速度矩分布控制的混流泵叶轮设计方法，具有设计效率高、模块结构清晰等特点；邴浩等^[8]和韩亚东等^[9]进一步分析了速度矩分布参数对混流泵能量特性和流场特性的影响规律；谭磊等^[10]提出了离心泵叶轮正反迭代设计方法，将正问题流场计算和反问题叶片设计相结合，通过迭代收敛得到最终的叶轮设计方案。谭磊等^[11-12]进一步将叶片载荷控制方法应用于气液两相混输泵的叶轮和导叶设计，实现了提升效率和抑制压力脉动的目的；王福军等^[13]提出了离心泵叶轮交替加载设计方法，采用前盖板前加载和后盖板后加载的模式，以提升效率和抑制压力脉动；王超越等^[14]指出势转子焓梯度(RPG)是叶轮内二次流产生的主因，提出了通过调节RPG分布抑制二次流的广义交替加载技术；薛城等^[15]采用正交试验法优化控制叶片载荷的5个参数，使得叶轮流态得到明显改善。

已有的叶片载荷控制方法在提升离心泵效率和稳定性方面取得了很好的效果。当前，离心泵面临宽工况高效稳定运行的更高要求，因此本文基于三段四次函数控制叶片载荷分布，提出了一种离心泵叶轮的设计方法，应用该方法完成了一台比转速为102的离心泵叶轮设计，采用数值模拟分析其内部流动特性，搭建流体机械综合试验台测试其能量特性。

叶轮叶片载荷为叶片压力面与吸力面的压差，叶片载荷与速度矩关系如下：

其中：p⁺为压力面压力；p^-为吸力面压力；ρ为流体密度；B为叶轮的叶片数；W_m为轴面相对流速；C_u为周向速度；r为径向距离；m为轴面流线相对长度，$ m=\frac{l}{l_{\max }} $，l为轴面流线长度，l_max为叶片出口对应的轴面流线长度；$ \frac{\partial C_{\mathrm{u}} r}{\partial m} $为载荷分布，可表示为L(m)。

叶片骨线方程如下：

其中：φ为叶片包角，U为牵连速度，C_m为轴面速度。叶轮轴面流道形状确定后，流线上任意一点的U和C_m可相应求解，给定速度矩C_ur沿轴面流线的变化规律，可得到叶片三维几何形状。

因此，调节L(m)从叶轮进口到出口的变化规律，即可实现对叶轮三维造型的精确控制。

相对于速度矩，叶片载荷能更直观地描述叶片做功过程，并可实现对该过程的精细控制。将叶片载荷沿叶轮进口到出口分为进口段、中间段和出口段，每段给定四次函数型载荷分布规律，构建基于三段四次载荷控制的叶轮设计方法。L(m)的三段四次分布规律如下：

其中：m从叶片进口到出口的取值范围为[0, 1]；m₁、m₂分别为前、后控制点的轴面流线相对长度；a_i、b_i、c_i、d_i、e_i(i=1, 2, 3)分别为三段四次函数的系数，求解全部系数需给定如下约束条件：

1) 进口段：起点(进口)载荷值L₀=L(0)，前控制点载荷值L₁=L(m₁)，起点载荷的一阶梯度值$ K_0=\frac{\mathrm{d} L(0)}{\mathrm{d} l} $，前控制点载荷的一阶梯度值K₁= $\frac{\mathrm{d} L\left(m_1\right)}{\mathrm{d} l} $，起点载荷的二阶梯度值K₀₀= $K_{00}=\frac{\mathrm{d}^2 L(0)}{\mathrm{d} l^2} $。

2) 中间段：前控制点载荷值L₁=L(m₁)，后控制点载荷值L₂=L(m₂)，前控制点载荷的一阶梯度值$ K_1=\frac{\mathrm{d} L\left(m_1\right)}{\mathrm{d} l}$，后控制点载荷的一阶梯度值$ K_2=\frac{\mathrm{d} L\left(m_2\right)}{\mathrm{d} l} $，前控制点载荷的二阶梯度值$ K_{11}=\frac{\mathrm{d}^2 L\left(m_1\right)}{\mathrm{d} l^2} $。

3) 出口段：后控制点载荷值L₂=L(m₂)，终点(出口)载荷值L₃=L(1)，后控制点载荷的一阶梯度值$K_2=\frac{\mathrm{d} L\left(m_2\right)}{\mathrm{d} l} $，终点载荷的一阶梯度值$ K_3=\frac{\mathrm{d} L(1)}{\mathrm{d} l}$，后控制点载荷的二阶梯度值$ K_{22}=\frac{\mathrm{d}^2 L\left(m_2\right)}{\mathrm{d} l^2}$。

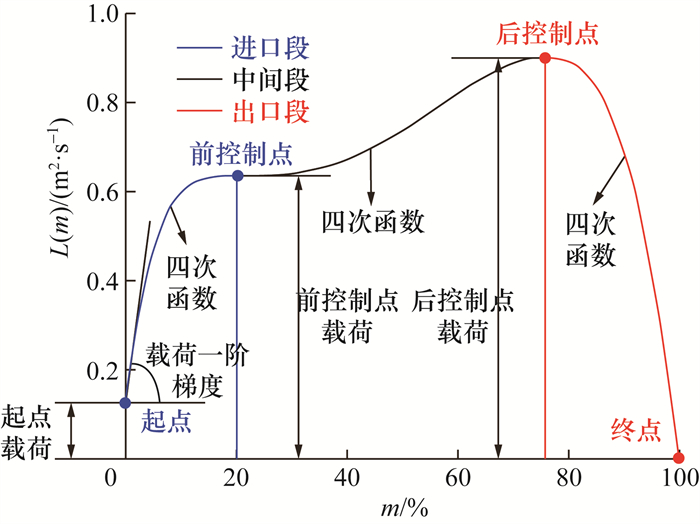
根据上述约束条件，可以获得三段四次函数的全部13个控制参数：m₁、m₂、L₀、L₁、L₂、L₃、K₀、K₁、K₂、K₃、K₀₀、K₁₁、K₂₂。设计过程中为各参数赋值即可求解式(3)中函数的全部系数，获得对应的三段四次载荷分布。本文针对一台比转速为102的离心泵叶轮，基于三段四次函数控制叶片载荷分布的示意图如图 1所示。由图可知，前、后控制点控制载荷进口段、中间段、出口段所占的轴面流线相对长度，改变L₀、L₁、L₂、L₃、K₀、K₁、K₂、K₃、K₀₀、K₁₁、K₂₂等参数可调整进口段、中间段、出口段载荷曲线的形状，实现载荷的精确控制。

图 1 三段四次载荷分布示意图

图选项

本文提出的设计方法的流程如下：1) 给定离心泵叶轮流道和叶片数；2) 划分轴面流道网格，求解轴面速度；3) 分别给定起点、前控制点、后控制点和终点的载荷、载荷一阶梯度值和载荷二阶梯度值；4) 求解四次函数待定系数，得到载荷分布规律；5) 根据载荷分布规律完成叶轮设计。

本文研究的离心泵的几何模型设计参数如表 1所示。

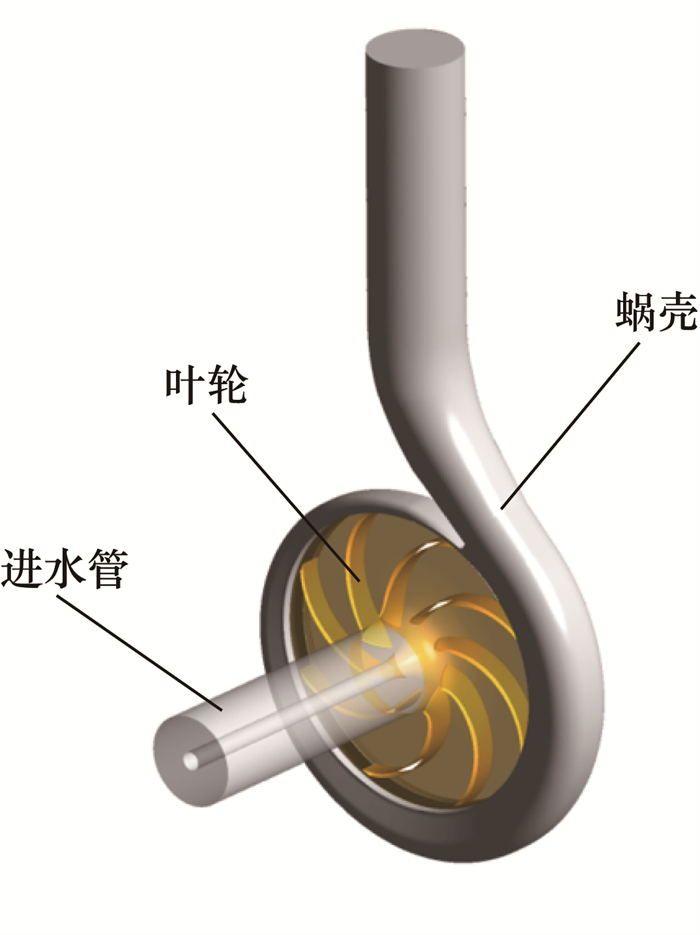
离心泵三维模型如图 2所示，主要包括进水管、叶轮和蜗壳。

图 2 离心泵三维模型

图选项

本文采用ANSYS CFX软件对离心泵开展数值模拟。由于RNG k-ε湍流模型能够较好地处理大曲率、强旋转、高应变率流动并广泛应用于离心泵性能预测^[16-17]，因此本文采用RNG k-ε湍流模型封闭Navier-Stokes方程。壁面设置为无滑移，进口边界条件为总压，出口边界条件为质量流量。静止和转动计算域之间采用冻结转子法连接。对流项和湍流数值求解均采用高分辨率格式。残差收敛精度为10^-5。

叶轮采用Turbogrid软件、进水管和蜗壳采用ICEM软件划分结构化网格。各部分网格质量均在0.4以上，满足网格质量要求。在网格无关性验证中，对4套不同数量的网格开展数值计算，结果如表 2所示。当总网格数量达到3 128 552个后，泵的扬程和效率变化不超过0.02%，满足无关性要求。因此，本文后续工作采用网格3开展研究。

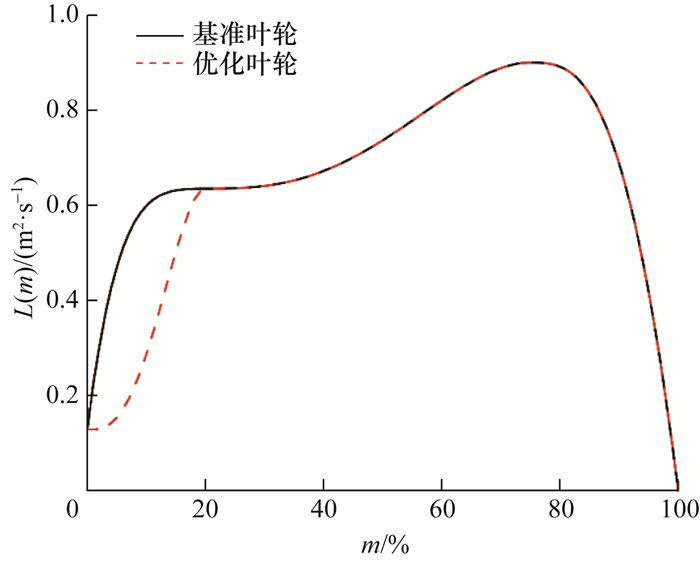
基准叶轮和优化叶轮的载荷分布规律如图 3所示。基准叶轮为课题组已有叶轮，保持基准叶轮载荷控制参数L₀、L₁、L₂、L₃、K₁、K₂、K₃、K₁₁、K₂₂不变，调整K₀、K₀₀得到优化叶轮。由图可知，基准叶轮进口段载荷从起点开始迅速上升，靠近前控制点附近平稳过渡；中间段载荷由前控制点缓慢上升，至后控制点处又趋于平稳；出口段载荷自后控制点起迅速下降至0。而优化叶轮进口段载荷在起点附近缓慢增大，靠近前控制点附近迅速上升。

图 3 不同载荷分布规律

图选项

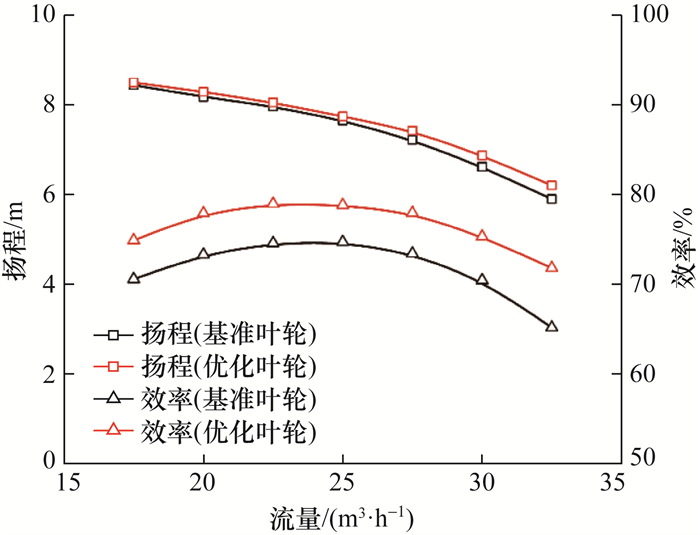
不同载荷分布规律下离心泵的能量特性如图 4所示。相比基准叶轮，优化叶轮的扬程几乎不变，在设计点的效率提高了4.11%，不同工况平均效率提高了5.35%。

图 4 不同载荷分布规律下离心泵的能量特性

图选项

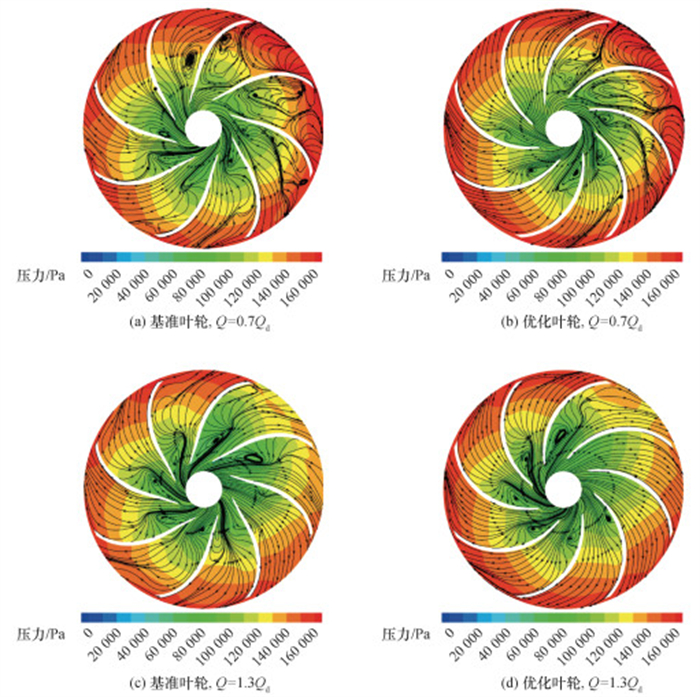
进一步选取50%叶高截面分析小流量(Q=0.7 Q_d)和大流量(Q=1.3 Q_d)工况下叶轮内部流场，如图 5所示。

图 5 叶轮内部压力和流线分布

图选项

在Q=0.7 Q_d工况下，基准叶轮内分离涡出现在叶片进口和叶片中部的吸力面侧，面积较大，部分漩涡甚至占据整个流道，导致泵的性能下降。优化叶轮内分离涡同样出现在叶轮进口和叶片中部的吸力面侧，但漩涡面积和强度显著减小。基准叶轮和优化叶轮内，沿进口到出口压力逐渐增大。基准叶轮出口处压力分布不均匀，沿流动方向的梯度变化较大，优化叶轮内压力分布更加均匀。

在Q=1.3 Q_d工况下，基准叶轮内分离涡出现在叶片进口吸力面侧，分布在各个流道。优化叶轮内叶轮进口吸力面侧同样存在分离涡，但其面积和数量明显减少，部分流道内的分离涡消失。

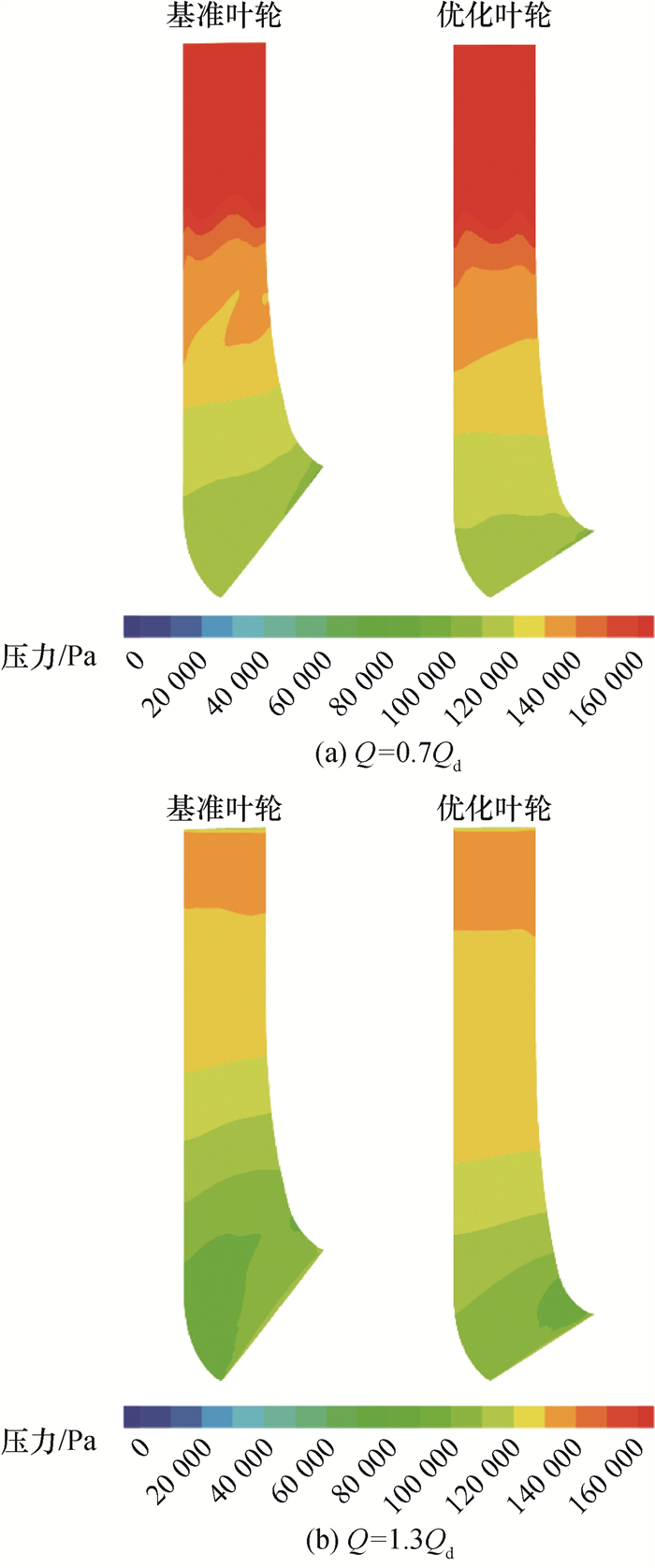
叶片表面压力分布如图 6所示。在Q=0.7 Q_d工况下，基准叶轮的压力在叶片中部存在明显不均匀区域，而优化叶轮的压力沿进口到出口均匀变化。在Q=1.3 Q_d工况下，基准叶轮压力在进口附近分布不均，轮毂侧低压区面积较大，而优化叶轮压力在进口附近的不均匀低压区显著缩小，叶片中后部压力缓慢增大。

图 6 叶片压力面的压力分布

图选项

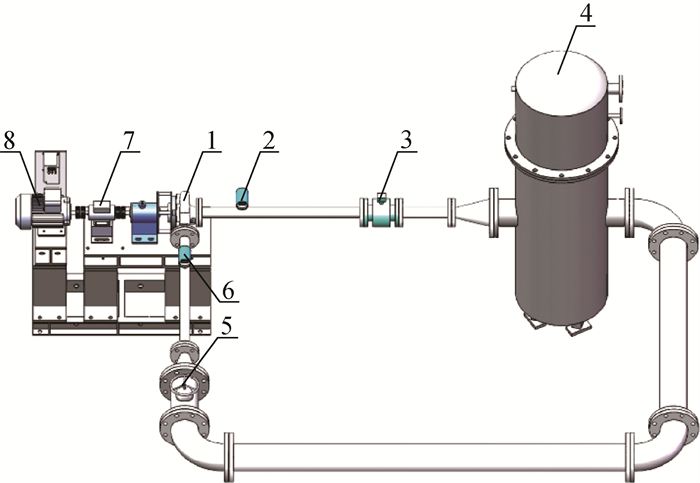
本文搭建了离心泵试验测量平台，位于清华大学能源与动力工程系中的水圈科学与水利工程全国重点实验室，主要由测试泵段、闭式管路、稳流罐和测量系统等组成，如图 7所示。测量仪器包括：电磁流量计，型号为KEFA，量程为0~200 m³/h，测量精度为0.3%；压力传感器，型号为Rosemount 3051，量程为0~200 kPa，测量精度为0.065%；转矩转速传感器，型号为ZH07-A-10，量程为0~10 N·m，测量精度为0.2%。测量过程中，离心泵启动并保持稳定转速后，调节阀门开度以调节流量，采用数据采集系统同步获取泵的进口压力、出口压力、流量、转速和扭矩等。

1—测试泵段；2—进口压力传感器；3—电磁流量计；4—水箱；5—出口球阀；6—出口压力传感器；7—转矩转速传感器；8—驱动电机 图 7 离心泵试验测量平台

图选项

采用五轴加工方法对优化叶轮进行加工，叶轮实物如图 8所示。

图 8 离心泵叶轮实物图

图选项

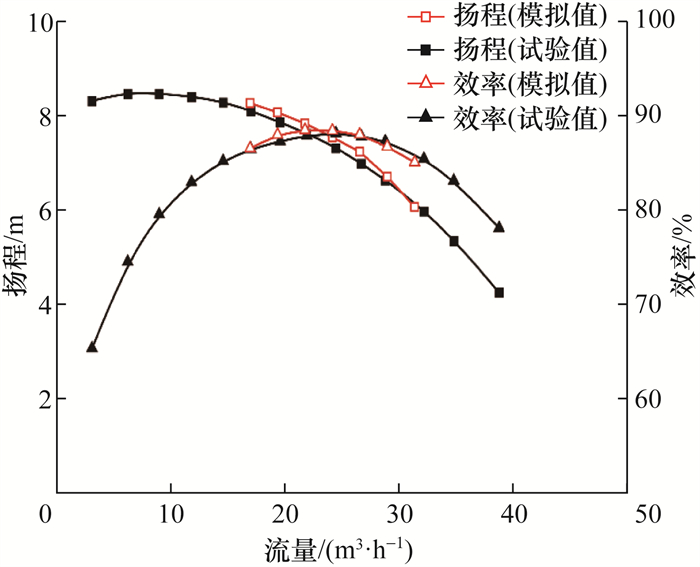
离心泵的流量-扬程和流量-效率曲线如图 9所示。由图可知，基于本文三段四次载荷控制方法设计的离心泵高效运行区平坦宽广，离心泵的最高效率为78.20%，对应的流量为25.32 m³/h，扬程为7.49 m，满足设计要求。

图 9 离心泵的数值模拟与试验测量结果

图选项

同时，将离心泵的数值模拟结果与试验测量结果进行对比，发现两者吻合较好，扬程和效率误差小于5%，验证了数值计算方法的可靠性和准确性。

本文提出了一种基于三段四次载荷控制的离心泵叶轮设计方法，对一台离心泵开展了叶轮设计、数值模拟和试验测量工作，主要结论如下：

1) 将叶片载荷沿叶轮进口到出口分为进口段、中间段和出口段三段，每段给定四次函数型载荷分布规律，构建了基于三段四次载荷控制的离心泵叶轮设计方法，能够实现叶轮三维造型的精确控制。

2) 载荷分布规律对离心泵能量特性和内部流场特性影响较大，进口段载荷在起点附近缓慢增大有利于提升内部流场均匀性，优化叶片表面压力分布，并提升离心泵效率。

3) 试验测量结果表明，离心泵高效运行区平坦宽广，满足设计要求。