2. 清华大学 水利水电工程系, 水沙科学与水利水电工程国家重点实验室, 北京 100084
2. State Key Laboratory of Hydroscience and Engineering, Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, China
桶形基础是海洋工程中被广泛使用的一种基础形式[1-2]。其中,插入式钢圆筒结构形式简单,便于快速施工,建成的码头、防波堤、护岸、围堰等建筑物稳定性良好,因此越来越多地被应用到海洋工程中[3-8]。制作完成的钢圆筒需要采用施工手段插入土中,一般采用低成本、高工效的振动式沉桩方法,其工作原理为:振动锤与桩刚性连接形成一个振动体系,振动锤通过以相同的角速度转动多组成对的偏心轮获得正弦振动力,进而带动桩体振动,桩体的振动使桩体周围的土层弱化或液化,桩受到的沉入阻力减小,桩锤体系在自重和激振力的作用下沉入土层 [8-11]。钢圆筒能否通过振动沉桩方法沉入土中指定深度,与钢圆筒自身构造、振动锤型号及数量、场地土层条件等多种因素有关。目前,针对钢圆筒振沉能力的定量评估方法已有大量研究成果[3, 12-16]。
近年来,中国多次采用大直径钢圆筒快速成岛的方法建设人工岛,取得了巨大的成功[17-19]。在类似人工岛建设这样的大型工程中,往往需要采用超大直径的钢圆筒,而钢圆筒直径是制约振沉能力的重要因素之一。钢圆筒直径越大,其侧表面积越大,端部面积也越大,在沉入过程中将受到更大的动侧壁摩阻力和端部阻力,因此越难沉入土中。在给定的场地条件、激振条件和钢圆筒构造下,存在一个最大的可沉入钢圆筒直径,超过这一直径的钢圆筒将不能沉入指定深度。在工程的设计阶段,应当充分考虑钢圆筒最大可沉入直径这一限制条件,以确保工程方案的合理性和可行性。然而,目前鲜有文献对此课题进行研究。
在评估钢圆筒的振沉能力时,场地土层条件的获取较为困难,需要进行大量土工试验。振沉分析所需的土层参数主要是土层的抗剪强度指标,要精确获得这些指标往往需要对大量的原状试样进行室内三轴试验,经济成本与时间成本都十分高昂。原位测试相比室内试验可以更经济、更快速地获取土层信息并为工程设计提供依据。标准贯入试验(standard penetration test, SPT)是目前岩土工程中最常用的原位测试方法之一,该试验得到的土层参数,标贯击数N,反映了土层的密实程度,可以用于快速估计土层的模量和抗剪强度指标。国内外的大量研究表明,标贯击数与抗剪强度指标存在显著的相关性,并已提出多种经验公式进行定量描述[20-25]。
本文提出了一种基于标贯击数快速评估给定土层条件下钢圆筒振沉能力并确定钢圆筒最大可沉入直径的方法,可以快速确定当前的钢圆筒构造、振动锤型号等方案在目标场地的可行性,为钢圆筒结构设计及优化提供参考。基于该方法,本文进一步讨论了不同土层性质及土层的分层情况下土层标贯击数对钢圆筒振沉能力的影响,相关的研究结果可以为定性判断钢圆筒沉入的难易程度提供参考。
1 钢圆筒振沉能力的计算方法国内外的文献已提出多种定量计算钢圆筒振沉能力的方法。本文将以中华人民共和国交通运输部发布的《插入式钢圆筒结构设计与施工规范》(JTS 167-13-2019)[3]建议的振沉能力计算方法为基础,对钢圆筒的振沉能力进行评估。按照该规范的要求,钢圆筒的振沉能力验算应包括激振力的验算和钢圆筒振幅的验算两部分。
1.1 激振力的验算钢圆筒振动下沉过程中的沉入动力为振动系统自身重力和振动锤锤组产生的激振力,沉入阻力为端部所受的土体施加的端部阻力和侧壁受到的土体施加的动侧壁摩阻力。激振力验算的目的在于评估当前选用的振动锤锤组方案所能施加的最大激振力能否满足振沉全过程中沉入动力始终大于沉入阻力的要求。
根据《插入式钢圆筒结构设计与施工规范》(JTS 167-13-2019)[3]中激振力验算部分的相关规定,要使钢圆筒顺利沉入水下指定深度,振沉期间的激振力应当满足
| $ F>K\left(Q_{\mathrm{SV}}+Q_{\mathrm{R}}\right) . $ | (1) |
其中:F表示振动锤锤组施加的激振力(kN);QSV表示钢圆筒沉入时所受动侧壁摩阻力(kN);QR表示钢圆筒沉入时所受的端部阻力(kN);K为激振力富裕系数,一般取1.2~1.5,有助沉措施时可以取小值。
端部阻力QR包括所有构件的端部受到的土体阻力,可以按照公式
动侧壁摩阻力QSV可通过钢圆筒所受的极限侧摩阻力QS折减得到。极限侧摩阻力QS按照
| $ \mu>\mu_{\min }+\left(1-\mu_{\min }\right) \mathrm{e}^{-0.52 \eta} . $ | (2) |
其中η=a/g是振动加速度幅值a与重力加速度g的比值。理论而言,振动加速度幅值应通过Newton第二定律按照a = F/m0求得(其中m0为钢圆筒与振沉设备中参与振动部分的质量之和,kg),但在设计时并不知道当前施加的激振力F的大小,因此以动侧壁摩阻力QSV代替激振力F计算振动加速度,这样得到的振动加速度比实际的小,是一种偏于安全的做法。又根据QSV=μQS得到
| $ \eta=\left(\mu Q_{\mathrm{S}}\right) / G_0 . $ | (3) |
其中G0=m0g是钢圆筒与振沉设备中参与振动部分的重量之和。联立方程(2)和(3)即可以求得各土层的摩阻力降低系数μj。
1.2 钢圆筒振幅的验算根据《插入式钢圆筒结构设计与施工规范》(JTS 167-13-2019)[3]中钢圆筒振幅验算的相关规定,振沉过程中钢圆筒振幅需大于各土层要求的最小振幅。
钢圆筒振幅为
| $ A=2 M / G_0 . $ | (4) |
式中M为锤组可提供的最大偏心力矩(kN·m)。
钢圆筒在不同土层中振沉所需的最小振幅与土层性质及土层的标贯击数N有关,如表 1所示。
2 标贯击数与抗剪强度指标的关联
振沉能力的计算使用到的土层参数主要是土层的抗剪强度指标:黏土采用不排水抗剪强度cu,砂土采用有效摩擦角φ′。要精确地获取场地土层的抗剪强度指标,需要取得各土层的代表性原状土样开展三轴试验等室内试验,时间成本高昂,不利于工程项目的快速推进。标准贯入试验是一种能够快速获取土层性质的原位测试方法,利用获得的标贯击数N换算成为抗剪强度指标可以更快速地对钢圆筒的振沉能力进行评估,进而论证所选方案的可行性。
学者们已经开展过大量的将土层标贯击数N与黏土不排水抗剪强度cu或砂土有效摩擦角φ′关联起来的研究并建立了经验公式,其中应用比较广泛的经验公式有Hara等[20]1974年提出的将cu与修正为标准应力波能量比的标贯击数N60关联起来的公式cu/pa=0.29N600.72,以及Kulhawy和Mayne[21]1990年提出的将φ′与N60关联起来的公式tan φ′=(N60/(12.2+20.3(σ′/pa)))0.34。其中:pa是标准大气压,可以取100 kPa;σ′为上覆有效应力。
由于中国工程中往往采用标贯击数N而不是N60进行设计,且不同国家、地区的土层性质存在差异,本文参考上述经验公式,直接建立关联标贯击数N与抗剪强度指标的经验公式:
| $ c_{\mathrm{u}}=a N^b . $ | (5) |
| $ \tan \varphi^{\prime}=d\left(N /\left(12.2+20.3\left(\sigma^{\prime} / p_{\mathrm{a}}\right)\right)\right)^f. $ | (6) |
根据工程建设场地或其附近区域已有的地质勘探资料可以标定上述经验公式中的参数a、b、d、f。
下面以国内某工程的实地情况为例,说明上述参数a、b、d、f具体的标定过程。该工程已通过地质勘探获得各土层的有效容重、标贯击数和抗剪强度指标,如表 2和图 1所示。
| 层厚/m | 有效容重/ (kN·m-3) | 黏土不排水抗剪强度cu/kPa | 砂土有效摩擦角φ′/(°) |
| 1.2 | 7.3 | 6 | |
| 0.6 | 8.1 | 39 | |
| 2.4 | 8.8 | 25 | |
| 0.8 | 8.5 | 35 | |
| 2.6 | 8.8 | 30 | |
| 2.7 | 9.0 | 35 | |
| 4.0 | 9.1 | 60 | |
| 1.3 | 9.2 | 20 | |
| 1.9 | 9.0 | 73 | |
| 2.0 | 8.9 | 76 | |
| 9.7 | 9.3 | 35 | |
| 2.5 | 9.2 | 135 | 25 |
| 2.4 | 9.5 | 120 | |
| 1.8 | 9.4 | 30 | |
| 5.4 | 9.7 | 130 |
|
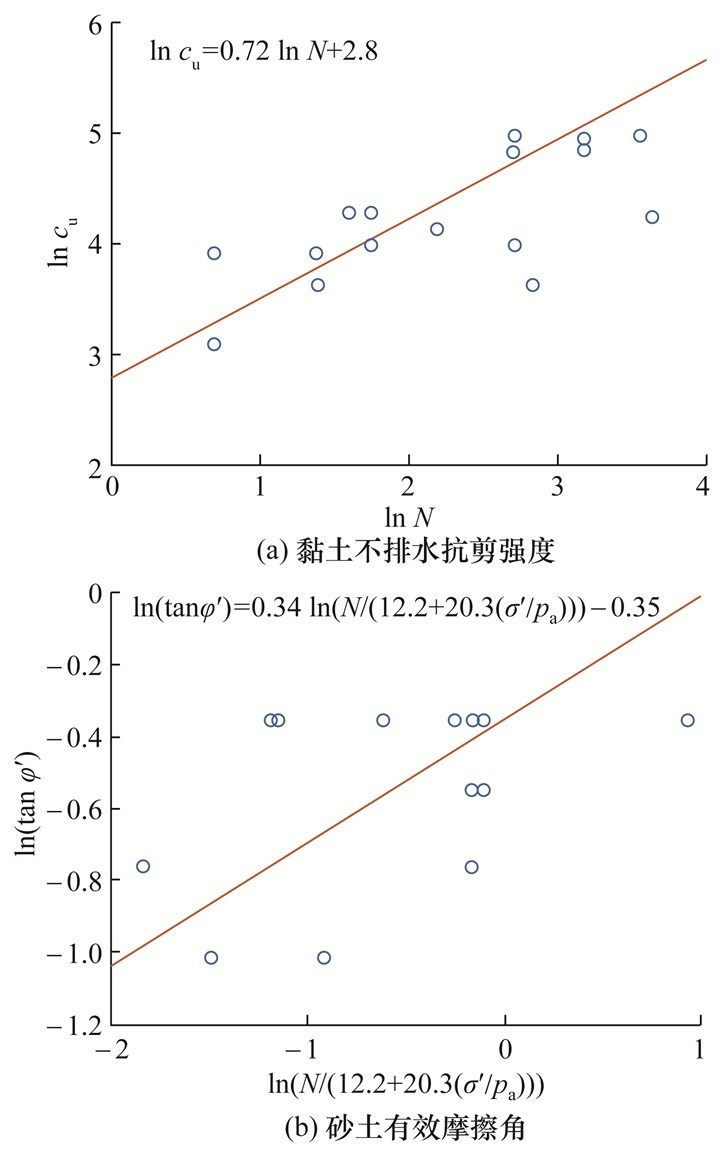
| 图 1 标贯击数与抗剪强度指标的经验关联公式参数标定 |
式(5)和(6)两边取对数可得ln cu=blnN+ln a和ln(tanφ′)=fln(N/(12.2+20.3(σ′/pa)))+ln d,通过拟合直线即可标定参数。如图 1所示,根据地勘资料,通过拟合可以确定4个参数:a=e2.8、b=0.72、d=e-0.35、f=0.34。
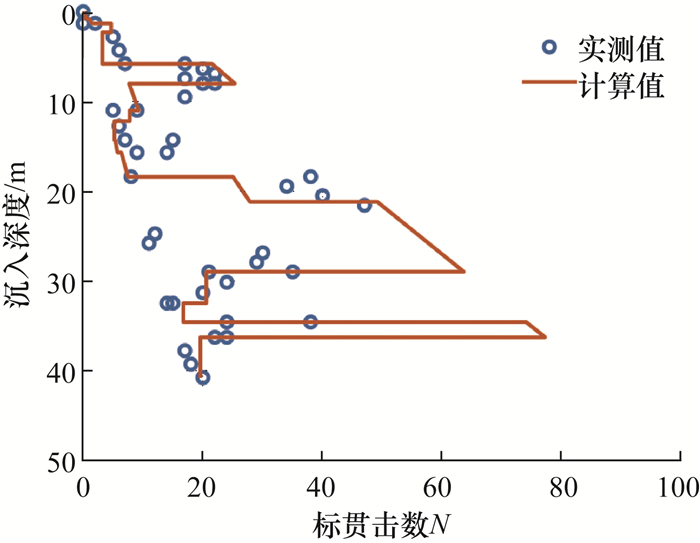
如图 2所示,使用式(5)和(6)由抗剪强度指标计算得到的标贯击数与实测标贯击数可以良好对应。当标贯击数较大时,由抗剪强度指标计算得到的标贯击数值与实际值偏离较大。这是因为式(5)和(6)主要是基于标贯击数较小时的数据得到的,对于标贯击数较大的情况,适用性较差。但是,工程中使用的钢圆筒沉入深度通常较浅,在本文计算示例中设计沉入深度为15 m,振沉过程中贯穿的土层的标贯击数较小,因此适用本文提出的方法。
|
| 图 2 标贯击数经验公式计算值与实测值的对比 |
通过已有数据标定得到经验公式的4个参数后,即可按照式(5)和(6)建立该区域内土层标贯击数与抗剪强度指标的关系。在该区域开展钢圆筒沉入选址工作时,只需在新场地上开展标准贯入试验并通过上述关系将获得的标贯击数换算成各土层的抗剪强度指标,即可快速地对钢圆筒的振沉能力进行评估。
3 通过标贯击数确定钢圆筒最大可沉入直径钢圆筒的直径越大,其侧面积和底面积越大,在振沉中受到的动侧壁摩阻力和端部阻力越大,振沉难度越大。因此,在一定的施工条件下,存在钢圆筒最大可沉入直径,超过此直径的钢圆筒将不能沉入预定深度。
3.1 计算思路根据《插入式钢圆筒结构设计与施工规范》(JTS 167-13-2019)[3]对振沉能力计算的相关规定,分析标贯击数和钢圆筒直径对钢圆筒振沉能力的影响,如图 3所示。
|
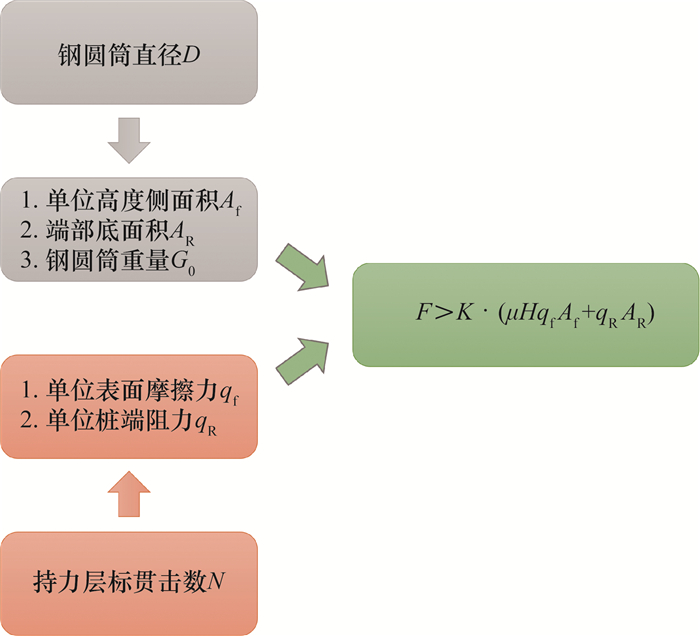
| 图 3 标贯击数N与钢圆筒直径D在激振力验算中的关联 |
首先,对激振力进行验算。在激振力验算中,钢圆筒直径增大产生的影响包含两个方面:1) 增大了钢圆筒与土接触的侧壁面积和端部面积,进而增大了侧壁摩阻力和端部阻力;2) 引起钢圆筒质量增加,降低了振动加速度,从而使周围土体弱化的程度降低,侧壁摩阻力折减程度降低。这两种影响均表现为沉入阻力随钢圆筒直径增大而增大。土层的标贯击数则反映了土层的抗剪强度,标贯击数越高表明土层越坚实,抗剪强度指标越高,单位侧壁摩阻力和单位桩端阻力越高,钢圆筒越难沉入。如图 3所示,钢圆筒直径和土层标贯击数通过规范规定的判别条件相互关联。本文选取K=1.5,根据式(1),在给定的土层条件下,可以得到唯一的钢圆筒最大可沉入直径。
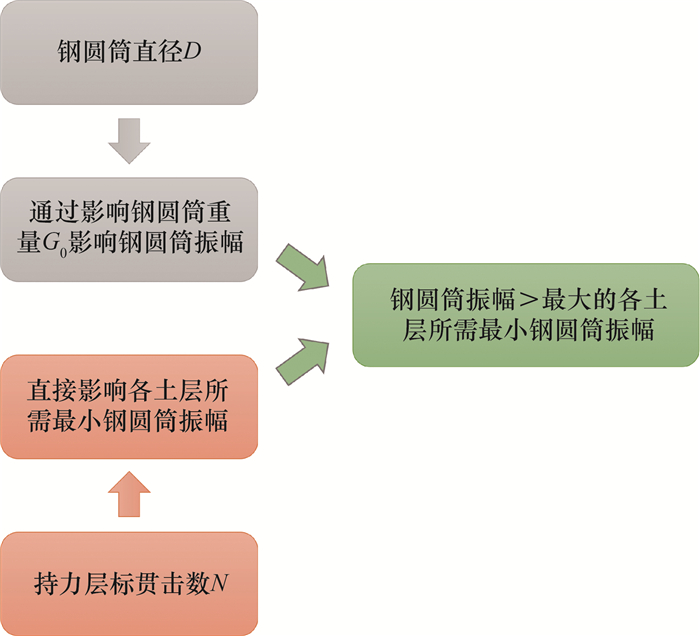
其次,考虑钢圆筒振幅的要求。根据式(4),钢圆筒直径不同,钢圆筒重量不同,而标贯击数则直接影响沉入各土层所需要的最小钢圆筒振幅。两者对钢圆筒振幅验算的影响如图 4所示。在给定的土层条件下,可以得到唯一的钢圆筒最大可沉入直径。
|
| 图 4 标贯击数N与钢圆筒直径D在振幅验算中的关联 |
要使钢圆筒沉入指定位置,需同时满足激振力的要求和振幅的要求,因此应选取上述两方面验算得到的钢圆筒最大可沉入直径中的较小值作为最终的钢圆筒最大可沉入直径。本文以一个具体的计算模型为例,具体呈现该计算方法的流程。
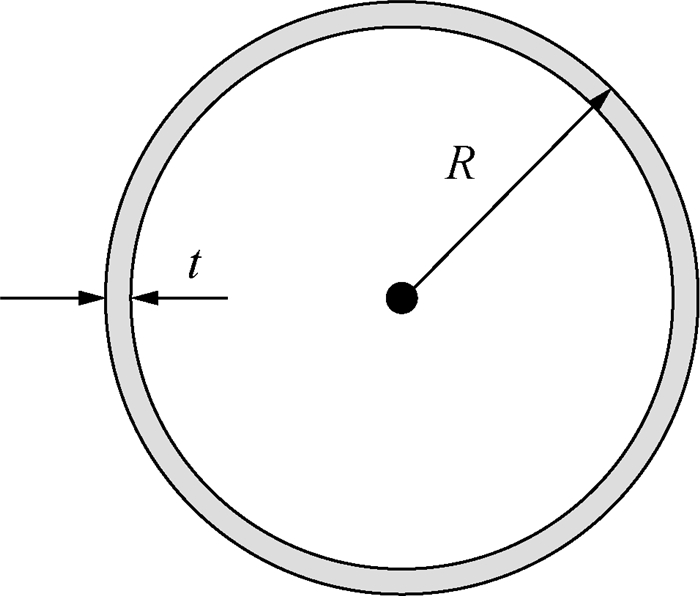
3.2 计算模型在实际工程中,采用的钢圆筒常常带有环肋、纵肋等附属构件以提高钢圆筒强度,从而避免钢圆筒在振沉或正常运行过程中出现破坏或屈曲。本文为方便分析钢圆筒最大可沉入直径,不考虑钢圆筒直径对附属结构尺寸的影响。假设钢圆筒模型为无任何附属构件的薄壁钢圆筒,且筒壁厚度处处相等。一个无附属构件的钢圆筒的俯视图如图 5所示。本文后续分析中仅考虑直径D=2R(R即为钢圆筒半径)的影响,厚度t和高度H保持不变。
|
| 图 5 无附属构件的钢圆筒的俯视图 |
无附属构件的钢圆筒单位高度侧壁面积为Af=2πR,端部面积近似为AR=2πtR,重量为G0=ρ0g·2πtHR,其中ρ0为钢材密度,可按7 850 kg/m3取值[27]。可见,无附属构件的钢圆筒的单位高度侧壁面积、端部面积及重量均与半径R成正比,即与直径D成正比。对于有附属构件的钢圆筒,可以认为上述结论也近似成立。本文假设所采用的钢圆筒厚度t为0.05 m,高度H为15 m。
液压振动锤是一种适应水下施工的振动锤[8],常用于钢圆筒振沉。本文考虑振动锤锤组方案为12台APE-600液压振动锤联动。该型号振动锤的主要参数见表 3[28]。振沉设备(不含钢圆筒)中除了液压振动锤外,还包含夹具等其他部件,振沉设备中参与振动部分的总质量为620 t。本文假设不同直径的钢圆筒振沉设备中参与振动部分的质量相同。
本文默认所有土层都在水下。本文除了分析沉入深度对振沉的影响的部分外,其他分析中钢圆筒预定沉入深度均设定为15 m。
3.3 计算示例与现场验证当土层条件得到确定后,即可使用本文3.2节的计算模型计算钢圆筒最大可沉入直径。本文第2章介绍了国内某工程的地质勘探结果,并标定了由标贯击数换算抗剪强度指标所需的参数。下面以该场地为例,基于获得的土层标贯击数数据,评估该场地中钢圆筒最大可沉入直径。
按照2.1节的计算思路计算钢圆筒最大可沉入直径。1) 根据激振力验算方法计算最大可沉入直径。先假设一个初始的钢圆筒直径(例如24 m),在此直径的基础上计算激振力富裕系数K。若K>1.5,则使用更大的直径再次进行计算;若K<1.5则使用较小的直径再次进行计算;多次迭代直至K与1.5足够接近,这时得到的钢圆筒直径即为给定土层条件下满足激振力验算要求的钢圆筒最大可沉入直径Dmax, 1。2) 根据钢圆筒振幅验算方法进行最大可沉入直径计算。根据土层标贯击数,确定所有要穿过的土层中所需的最小振幅,求解出可沉入的最大钢圆筒质量,进而算出满足钢圆筒振幅验算要求的钢圆筒最大可沉入直径Dmax, 2。钢圆筒直径为Dmax=min(Dmax, 1,Dmax, 2),可以同时满足激振力验算要求和钢圆筒振幅要求,即为钢圆筒最大可沉入直径。
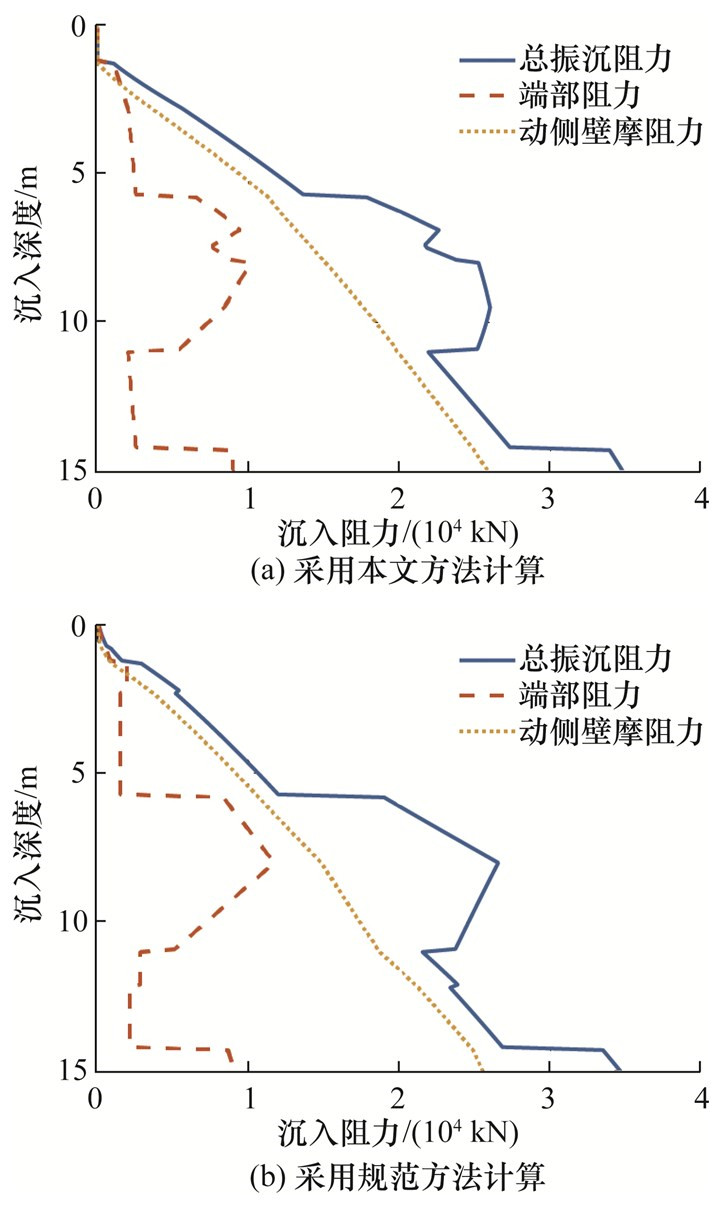
经计算,该场地条件下Dmax, 1=27.703 m,Dmax, 2=45.611 m,即该场地的钢圆筒最大可沉入直径为Dmax=27.703 m。当直径等于Dmax的钢圆筒沉入该场地时,沉入阻力随沉入深度的变化如图 6a所示。总振沉阻力为动侧壁摩阻力和端部阻力的总和。此时总振沉阻力在钢圆筒沉入最终深度15 m时取得最大值,为34 763 kN,恰使激振力富裕系数为1.5。
|
| 图 6 直径为27.703 m的钢圆筒振沉时所受沉入阻力 |
使用规范方法(直接使用土层的抗剪强度指标)对直径为D=27.703 m的钢圆筒进行计算,得到的沉入阻力随沉入深度的变化如图 6b所示,富裕系数K=1.51。对比图 6a和6b可以看到,本文提出的方法计算得到的各项沉入阻力随沉入深度的变化与规范方法的计算结果基本一致。
由图 6所示的沉入阻力随沉入深度变化曲线可知,随着沉入土中的钢圆筒部分越来越多,钢圆筒与土接触的侧面积越来越大,因此受到的动侧壁摩阻力单调增大;而钢圆筒受到的端部阻力主要与钢圆筒筒底目前所处的土层有关,因此在振沉过程中波动变化,即在坚实土层中钢圆筒受到的端部阻力较大、在软弱土层中受到的端部阻力则较小。
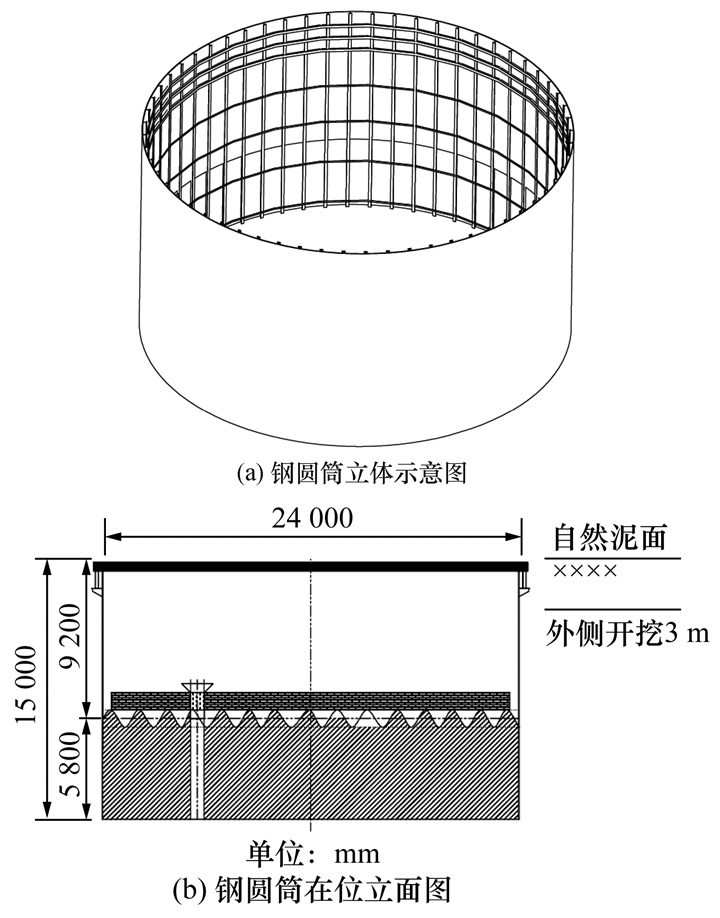
根据该工程的场地条件,最终采用直径为24 m的钢圆筒,预定沉入深度为15 m。如图 7所示,振沉前开挖3 m,振入到指定深度后内部开挖安装底板、顶板等。经过上述计算流程得到总振沉阻力在钢圆筒沉入最终深度15 m时取得最大值,为30 962 kN。现场实际采用的最大激振力为28 500 kN,相对误差为8%且计算偏保守。可见,本文提出的方法基本可靠。
|
| 图 7 某工程实际采用的钢圆筒 |
3.4 钢圆筒最大可沉入直径与均匀土层的标贯击数的关系
3.3节的计算示例使用了实际工程场地的复杂成层土层。本节采用概化的成层土层分析土层性质及土层的分层情况对振沉能力的影响。考虑一个土层土质及标贯击数沿深度不变的理想化场地模型,对于每一个确定的土层标贯击数N,有唯一的钢圆筒最大可沉入直径Dmax与之对应,可以绘制N-Dmax曲线,直观地呈现土层标贯击数与钢圆筒最大可沉入直径的关系。下文将假设土层标贯击数与抗剪强度指标间的关系符合经验公式(5)和(6),并采用本文第2章中标定得到的参数。下文中提到的黏土和砂土均指理想的黏土和理想的砂土,即黏土有效摩擦角φ′=0;砂土不排水抗剪强度cu=0。在不确定土层类型时,对某一标贯击数随深度的分布,应分别考虑黏土和砂土,取最不利的情况得到的最大可沉入直径作为该标贯击数对应的最大可沉入直径。
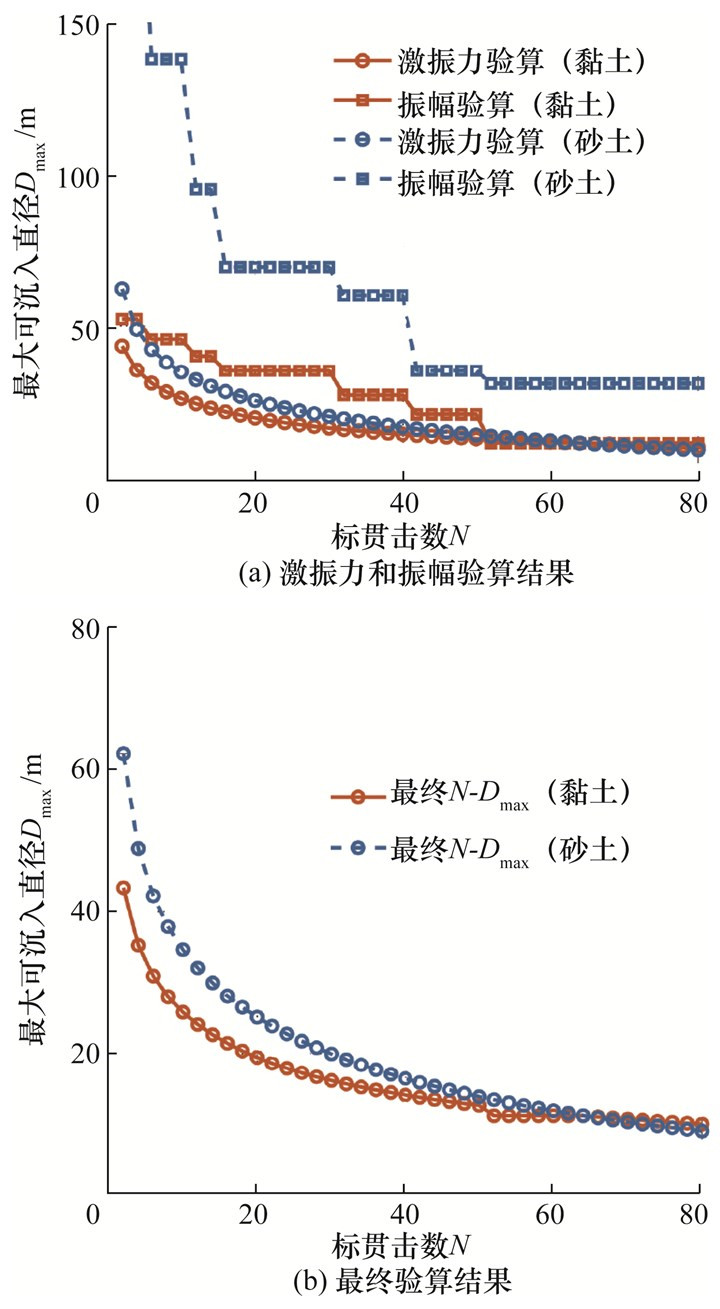
3.4.1 土层性质的影响即使标贯击数完全相同,黏土和砂土在钢圆筒振沉期间产生的阻力也存在显著不同。分别绘制出具有单一标贯击数的均匀黏土土层和砂土土层的N-Dmax曲线,如图 8所示。在激振力验算方面,当土层标贯击数较小时,砂土层中的钢圆筒最大可沉入直径比黏土层中的大;当土层标贯击数较大时,黏土层中的钢圆筒最大可沉入直径则比砂土层中的大。在钢圆筒振幅验算方面,从表 1所示的各类土层所需的最小钢圆筒振幅中可以看到,相同标贯击数下,砂土层要求的最小钢圆筒振幅比黏土层小很多,这表明钢圆筒在砂土层中更容易沉入,更大直径的钢圆筒可以满足要求。同时考虑激振力验算的要求和钢圆筒振幅的要求,可以发现在该工况下,激振力的要求是主导因素。
|
| 图 8 均匀黏土和砂土中的N-Dmax关系(预定沉入深度15 m) |
3.4.2 预定沉入深度的影响
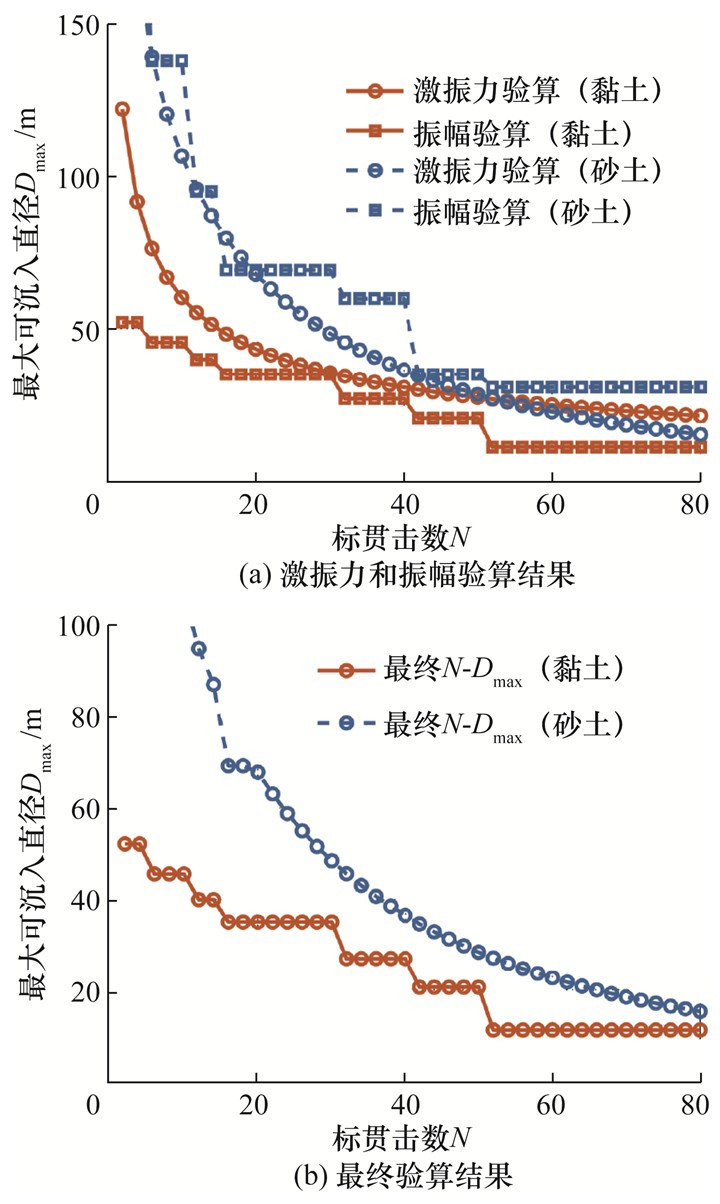
考虑部分钢圆筒沉入土中的情况。将钢圆筒的预定沉入深度设为5 m,绘制出此工况下的N-Dmax曲线,如图 9所示。由于计算模型中采用的是均匀土层,钢圆筒振幅验算与沉入深度无关,因此预定沉入深度为5 m时通过振幅验算得到的N-Dmax曲线与预定沉入深度为15 m时一致。在激振力验算方面,当预定沉入深度减小时,钢圆筒在振沉过程中受到的沉入阻力减小,因此预定沉入深度为5 m时通过激振力验算得到的N-Dmax曲线比预定沉入深度为15 m时显著要高。预定沉入深度为5 m时的N-Dmax曲线主要受振幅验算要求的控制。
|
| 图 9 均匀黏土和砂土中的N-Dmax关系(预定沉入深度5 m) |
总之,当预定沉入深度较浅时振幅验算的要求起主导作用,当预定沉入深度较深时激振力验算的要求起主导作用。
3.5 钢圆筒最大可沉入直径与含软弱或坚硬夹层的土层的标贯击数的关系实际的工程场地中的土层往往是成层土层,相比于均匀土层,钢圆筒的振沉问题更为复杂。为了分析成层土层中标贯击数对钢圆筒最大可沉入直径的影响,本节将讨论含有软弱或坚硬夹层的简化的土层模型,分析钢圆筒最大可沉入直径与软弱或坚硬夹层中的标贯击数的关系。由于钢圆筒的预定沉入深度为15 m,深度超过15 m的土层对振沉过程没有影响,因此仅对0~15 m的土层情况进行说明,同时为方便分析,假设标贯击数为16的砂土层中含标贯击数不同的砂土夹层。
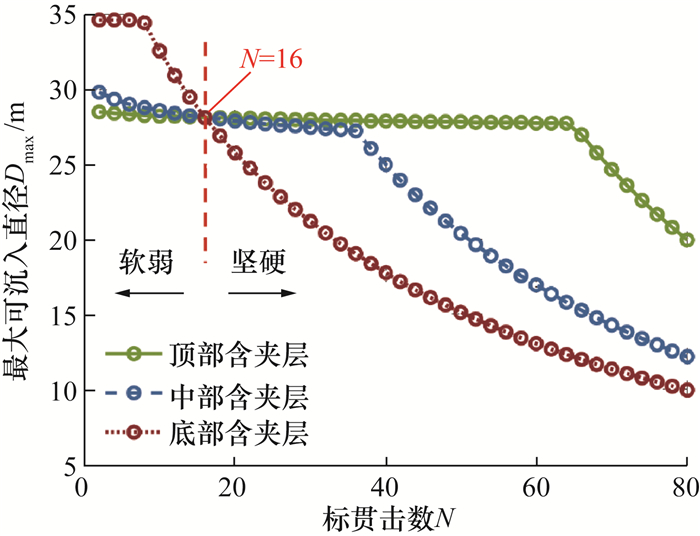
3.5.1 夹层位置的影响假设夹层厚度为3 m,分析夹层处于土层顶部(0~3 m)、中部(6~9 m)和底部(12~15 m)时夹层标贯击数N与钢圆筒最大可沉入直径Dmax的关系,由N-Dmax曲线表示,此处N表示夹层的标贯击数,其他土层的标贯击数为16。计算结果如图 10所示。
|
| 图 10 夹层处于不同位置时的N-Dmax曲线对比 |
这3种工况下均为激振力验算的要求起主导作用。最终得到的3条N-Dmax曲线在N=16处相交,此时夹层与其他土层的标贯击数一样,等价于标贯击数为16的均匀土层。夹层的标贯击数N<16表示存在软弱夹层,钢圆筒最大可沉入直径比均匀土层大;反之,夹层的标贯击数N>16则增大了振沉难度,钢圆筒最大可沉入直径比均匀土层小。对比夹层位置不同时的N-Dmax曲线可以发现,夹层位置显著影响钢圆筒的振沉能力,且夹层位置越接近底部对钢圆筒振沉的影响越大。
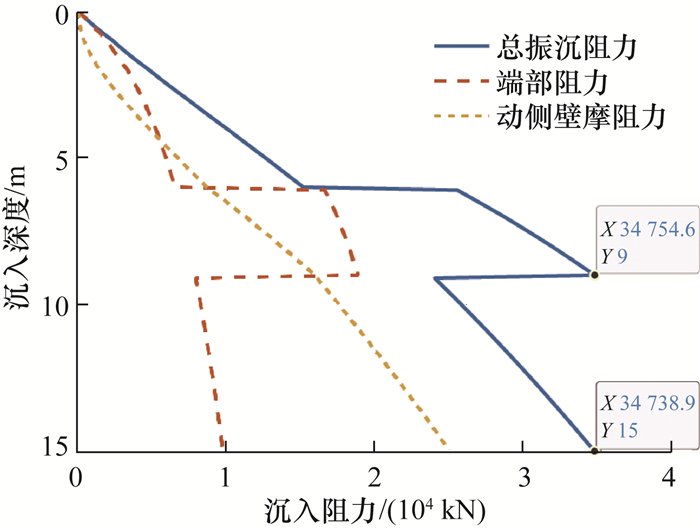
图 10所示的N-Dmax曲线均存在一个明显的转折点:当N较小时,Dmax随N的变化较缓慢,但当N超过临界值Nc时,Dmax随N的增大迅速减小。为探究这一现象,选取土层中部含夹层的情况进行分析,其临界标贯击数为Nc=36,对应的钢圆筒最大可沉入直径为Dmax=27.2 m。绘制出该工况下沉入阻力随沉入深度的变化,如图 11所示。
|
| 图 11 夹层标贯击数等于临界标贯击数时具有最大可沉入直径的钢圆筒在振沉过程中受到的阻力 |
由图 11可见,当夹层的标贯击数等于临界标贯击数Nc时,钢圆筒在沉入夹层底部时的总振沉阻力与沉入预定深度时的总振沉阻力接近。当夹层标贯击数小于临界标贯击数Nc时,振沉过程中总振沉阻力的最大值出现在沉入15 m时,此时钢圆筒的底部已经穿过夹层,因此夹层只通过影响动侧壁摩阻力而影响最终的振沉能力,振沉能力随标贯击数的变化较不显著;而当夹层标贯击数大于临界标贯击数Nc时,振沉过程中总振沉阻力的最大值将出现在沉入9 m时(夹层底部),因此振沉能力随标贯击数的增大显著减小。同理,当土层为软弱夹层且夹层不位于钢圆筒预定沉入深度时,夹层只通过影响动侧壁摩阻力影响振沉能力,此时软弱夹层对振沉能力的影响不显著。
夹层位于不同位置时,N-Dmax曲线的临界标贯击数Nc不同,夹层所处的位置越浅,临界标贯击数Nc越大。因此,当坚硬夹层位于较浅位置时,只有标贯击数很大的坚硬夹层对振沉能力有显著影响。
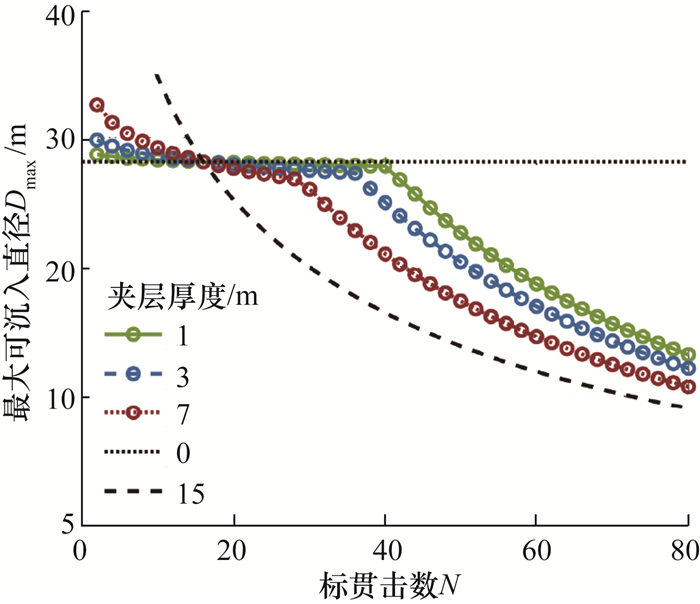
3.5.2 夹层厚度的影响为探究夹层厚度对N-Dmax曲线的影响,假设夹层位于土层中部,分析夹层厚度为1 m(夹层位于7~8 m)、3 m(夹层位于6~9 m)、7 m(夹层位于4~11 m)时夹层标贯击数N与钢圆筒最大可沉入直径Dmax的关系,其结果见图 12的N-Dmax曲线。
|
| 图 12 夹层具有不同厚度时的N-Dmax曲线对比(夹层中心深度:7.5 m) |
从图 12可以看到,夹层的厚度越大,对钢圆筒振沉能力的影响越大。图 12中还绘制出了夹层厚度为0 m和夹层厚度为15 m两种极端的情况。夹层厚度为0 m,即没有夹层,此时土层为标贯击数为16的砂土层,钢圆筒最大可沉入直径约为28.125 m,在图 12中是一条水平线。当夹层厚度为15 m时,整个土层即为标贯击数更大的均匀土层,此时得到的N-Dmax曲线与图 7中砂土的N-Dmax曲线相同。当夹层为其他厚度时,得到的N-Dmax曲线位于夹层厚度为0 m的N-Dmax曲线和夹层厚度为15 m的N-Dmax曲线之间,且随着厚度的增加,逐渐向夹层厚度为15 m的N-Dmax曲线靠近。
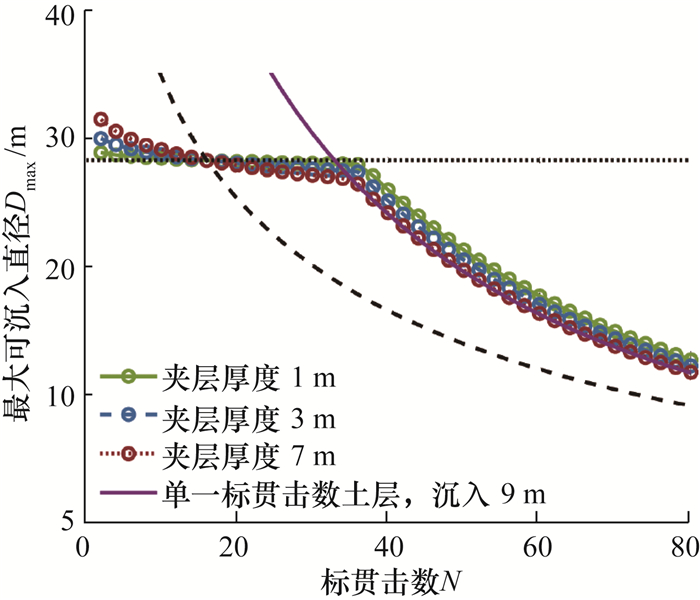
为排除夹层底部位置的影响,假设夹层底部位于9 m位置处不变,分析夹层厚度为1 m (夹层位于8~9 m)、3 m(夹层位于6~9 m)、7 m(夹层位于2~9 m)时夹层标贯击数N与钢圆筒最大可沉入直径Dmax的关系,其结果见图 13的N-Dmax曲线。图 13中夹层厚度为3 m的N-Dmax曲线与图 12中夹层厚度为3 m的N-Dmax曲线是一样的。
|
| 图 13 夹层具有不同厚度时的N-Dmax曲线对比(夹层底部深度:9.0 m) |
对比图 13和12可以发现,当夹层标贯击数小于临界标贯击数Nc时,夹层厚度和夹层底部位置均对N-Dmax曲线产生较轻微的影响,且两者影响程度接近;而当夹层标贯击数大于临界标贯击数Nc时,夹层底部位置对N-Dmax曲线的影响显著大于夹层厚度对N-Dmax曲线的影响。
4 结论本文提出了一种基于土层标贯击数估计钢圆筒最大可沉入直径的方法,该方法可以根据标贯试验的结果快速评估钢圆筒设计方案的可行性,为钢圆筒结构设计、优化提供参考。在此方法的基础上,本文建立了简化的计算模型,讨论了不同土层性质及土层的分层情况下的土层标贯击数对钢圆筒最大可沉入直径的影响,并得出如下结论:
1) 根据国内某工程现场的地勘结果和施工条件,本文提出的方法计算得到的最大可振入钢圆筒直径为27.7 m,对应的总振沉阻力曲线与规范方法计算结果基本一致。现场采用的钢圆筒直径为24 m,本文方法计算得到最大总阻力与现场记录的最大激振力相对误差为8%且计算偏保守。本文提出的方法基本可靠。
2) 对于具有相同标贯击数的黏土土层和砂土土层,当标贯击数较小时,黏土土层对钢圆筒振沉的阻碍作用更大,钢圆筒最大可沉入直径更小;当标贯击数较大时,砂土土层对钢圆筒振沉的阻碍作用更大。
3) 当钢圆筒的预定沉入深度较浅时,钢圆筒振幅验算的要求为钢圆筒振沉分析中的主导因素;当钢圆筒的预定沉入深度较深时,激振力验算的要求为钢圆筒振沉分析中的主导因素。
4) 当土层中含有软弱或坚硬夹层时,夹层的存在对振沉能力的影响程度与夹层的标贯击数有关,存在一个临界标贯击数:当夹层标贯击数小于这一临界值时,夹层的存在对振沉能力的影响较小;当夹层标贯击数大于这一临界值时,夹层的存在对振沉能力影响较大,钢圆筒最大可沉入直径随夹层标贯击数的增大迅速减小。夹层底部位置越深、夹层厚度越厚,夹层对振沉能力的影响越大,临界标贯击数越小。
| [1] |
杨春宝, 张建民, 王睿. 海上风电吸力桶基础地震分析[J]. 清华大学学报(自然科学版), 2017, 57(11): 1207-1211. YANG C B, ZHANG J M, WANG R. Seismic analysis of a suction caisson foundation for offshore wind turbines[J]. Journal of Tsinghua University (Science and Technology), 2017, 57(11): 1207-1211. DOI:10.16511/j.cnki.qhdxxb.2017.26.063 (in Chinese) |
| [2] |
王贺, 王睿, 张建民. 砂土中吸力桶安装过程离心机试验和数值模拟研究[J]. 中国科学: 技术科学, 2022, 52(12): 1792-1801. WANG H, WANG R, ZHANG J M. Centrifuge experiment and numerical simulation of suction caisson installation in sand[J]. Scientia Sinica Technologica, 2022, 52(12): 1792-1801. (in Chinese) |
| [3] |
中华人民共和国交通运输部. 插入式钢圆筒结构设计与施工规范: JTS 167-13-2019[S]. 北京: 人民交通出版社, 2019. Ministry of Transport of the People's Republic of China. Design and construction code of embedded steelplate cylinder structure: JTS 167-13-2019[S]. Beijing: China Communications Press, 2019. (in Chinese) |
| [4] |
杨晓非, 彭翔. 可速建速拆式临时码头设计选型与施工[J]. 建筑技术开发, 2018, 45(9): 41-43. YANG X F, PENG X. Design selection and construction of disassembled temporary wharf[J]. Building Technology Development, 2018, 45(9): 41-43. (in Chinese) |
| [5] |
宋波, 冯国俊, 王荣. 基于标准化水平残余位移的沉入式钢圆筒防波堤抗震性能研究[J]. 工程力学, 2018, 35(10): 183-192. SONG B, FENG G J, WANG R. Study on the aseismic performance of embedded steel cylinder breakwater for backfill sand foundation based on normalized residual horizontal displacement[J]. Engineering Mechanics, 2018, 35(10): 183-192. DOI:10.6052/j.issn.1000-4750.2017.08.0627 (in Chinese) |
| [6] |
李伟仪, 卢永昌. 插入式大直径钢圆筒岸壁结构的设计实践及应用前景[J]. 水运工程, 2004, 362(3): 24-29. LI W Y, LU Y C. Design and application prospect of large-diameter steel cylinder quay structure[J]. Port & Waterway Engineering, 2004, 362(3): 24-29. (in Chinese) |
| [7] |
黄明华, 汤小明, 刘世松. 填海造岛超大直径薄壁钢圆筒制作技术[J]. 钢结构, 2018, 33(6): 80-84. HUANG M H, TANG X M, LIU S S. Manufacturing technology of super large diameter thin-walled steel cylinder for artificial island[J]. Steel Construction, 2018, 33(6): 80-84. (in Chinese) |
| [8] |
刘宝河, 边强, 袁孟全. 振动沉桩锤的选型及应用[J]. 中国港湾建设, 2008(3): 38-41, 78. LIU B H, BIAN Q, YUAN M Q. Selection and application of vibratory piling hammers[J]. China Harbour Engineering, 2008(3): 38-41, 78. (in Chinese) |
| [9] |
林煌超. 饱和砂土层中钢管桩高频液压振动沉桩机理研究[D]. 昆明: 云南大学, 2018. LIN H C. Study on mechanism of high-frequency hydraulic vibration sinking of steel pipe pile in saturated sand layer[D]. Kunming: Yunnan University, 2018. (in Chinese) |
| [10] |
陈福全, 汪金卫, 李大勇, 等. 高频液压振动锤打桩的应用概况与研究进展[J]. 岩土工程学报, 2011, 33(S2): 224-231. CHEN F Q, WANG J W, LI D Y, et al. Application and advance of vibratory driving techniques using high-frequency hydraulic vibratory hammer[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 224-231. (in Chinese) |
| [11] |
罗春雷, 刘丹. 国外振动沉桩建模分析方法[J]. 建筑机械, 2005(6): 62-66. LUO C L, LIU D. Overseas analysis of vibratory pile driving[J]. Construction Machinery, 2005(6): 62-66. (in Chinese) |
| [12] |
SMITH E A L. Pile-driving analysis by the wave equation[J]. Journal of the Soil Mechanics and Foundations Division, 1960, 86(4): 35-61. DOI:10.1061/JSFEAQ.0000281 |
| [13] |
WONG D, O'Neill M W, VIPULANANDAN C. Modelling of vibratory pile driving in sand[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1992, 16(3): 189-210. DOI:10.1002/nag.1610160303 |
| [14] |
汪金卫, 陈福全, 简洪钰. 高频液压振动锤打桩的可打入性分析模型[J]. 福建工程学院学报, 2009, 7(1): 9-15. WANG J W, CHEN F Q, JIAN H Y. The models for vibratory driveability of piles by vibratory hammer[J]. Journal of Fujian University of Technology, 2009, 7(1): 9-15. (in Chinese) |
| [15] |
胥新伟, 刘亚平, 黎双邵. 大直径钢圆筒振沉计算方法[J]. 中国港湾建设, 2014(10): 14-16. XU X W, LIU Y P, LI S S. Calculating method for vibro-sinking large diameter steel caissons[J]. China Harbour Engineering, 2014(10): 14-16. (in Chinese) |
| [16] |
胥新伟, 刘亚平, 高潮. 大直径钢圆筒振动下沉可行性分析方法[J]. 中国港湾建设, 2016, 36(4): 9-11. XU X W, LIU Y P, GAO C. Feasibility analyzing method of vibration sinking of large diameter steel caissons[J]. China Harbour Engineering, 2016, 36(4): 9-11. (in Chinese) |
| [17] |
付院平, 李家林, 黄涛, 等. 人工岛围护结构钢圆筒及副格振沉装备与施工技术[J]. 中国港湾建设, 2019, 39(3): 52-56. FU Y P, LI J L, HUANG T, et al. Equipment and construction technology of steel cylinder and deputy vibration and sinking of enclosure structure of artificial island[J]. China Harbour Engineering, 2019, 39(3): 52-56. (in Chinese) |
| [18] |
刘健, 夏丰勇, 唐一夫. 深中通道西人工岛总体设计及大直径钢圆筒快速成岛技[J]. 水运工程, 2021(6): 13-19. LIU J, XIA F Y, TANG Y F. Overall design of western artificial island of Shenzhen-Zhongshan Link and rapid island-formation technology by large-diameter steel cylinder[J]. Port & Waterway Engineering, 2021(6): 13-19. (in Chinese) |
| [19] |
唐云, 李洋, 樊亮亮. 香港机场第三跑道填海工程插入式钢圆筒结构设计[J]. 水运工程, 2020(9): 180-185. TANG Y, LI Y, FAN L L. Design of inserted steel cylinder structure for third runway reclamation project of Hong Kong Airport[J]. Port & Waterway Engineering, 2020(9): 180-185. (in Chinese) |
| [20] |
HARA A, OHTA T, NIWA M, et al. Shear modulus and shear strength of cohesive soils[J]. Soils and Foundations, 1974, 14(3): 1-12. |
| [21] |
KULHAWY F H, MAYNE P W. Manual on estimating soil properties for foundation design[M]. Palo Alto, USA: Electric Power Research Institute, 1990.
|
| [22] |
HETTIARACHCHI H, BROWN T. Use of SPT blow counts to estimate shear strength properties of soils: Energy balance approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(6): 830-834. |
| [23] |
张占荣, 刘庆辉, 赵勇. 基于标贯试验特性的土体力学参数估计[J]. 勘察科学技术, 2010(6): 18-21. ZHANG Z R, LIU Q H, ZHAO Y. Estimation of soil mechanical parameters based on standard penetration test characteristics[J]. Site Investigation Science and Technology, 2010(6): 18-21. (in Chinese) |
| [24] |
胡增辉, 李家奇, 李晓昭, 等. 利用标准贯入试验确定粘性土的不排水抗剪强度[J]. 地下空间与工程学报, 2011, 7(S2): 1577-1582, 1588. HU Z H, LI J Q, LI X Z, et al. Determination of undrained shear strength of clayey soils by SPT value[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(S2): 1577-1582, 1588. (in Chinese) |
| [25] |
郭淋, 王春艳, 张飞, 等. 标贯试验N值与土体物理力学参数的相关性分析[J]. 安全与环境工程, 2012, 19(4): 148-152. GUO L, WANG C Y, ZHANG F, et al. Correlation analysis of SPT N-value and geotechnical physical mechanic parameters[J]. Safety and Environmental Engineering, 2012, 19(4): 148-152. (in Chinese) |
| [26] |
American Petroleum Institute. Geotechnical and foundation design considerations: API RP 2GEO-2014[S]. Washington, DC, USA: American Petroleum Institute, 2014.
|
| [27] |
中华人民共和国住房和城乡建设部. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2018. Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture Publishing, 2018. (in Chinese) |
| [28] |
上海振力工程机械设备有限公司. APE600液压振动锤[EB/OL]. [2022-08-18]. http://www.apezhenli.com/ape-400-%e5%9e%8b%e5%8f%b7-2/. Shanghai Zhenli Engineering Machinery Equipment Co., Ltd. Model 600 hydraulic vibratory hammer[EB/OL]. [2022-08-18]. http://www.apezhenli.com/ape-400-%e5%9e%8b%e5%8f%b7-2/. (in Chinese) |


