2. 中国矿业大学(北京) 矿山与城市固废资源化工程研究中心, 北京 100083;
3. 北京工业职业技术学院 建筑与测绘工程学院, 北京 100042
2. Engineering Research Center for Mining and Urban Solid Waste Recycling, China University of Mining and Technology (Beijing), Beijing 100083, China;
3. School of Architecture and Surveying Engineering, Beijing Polytechnic College, Beijing 100042, China
破碎作业是现代矿业及岩土工程中的关键环节之一。岩石作为一种天然介质,是破碎作业中最常见的材料。岩石破碎作业是通过外界各种形式的能量输入,使岩石按照后续工艺的需要破碎成生产要求的粒度的过程。岩石破碎的本质是岩石在外部能量驱动下的状态宏观失稳现象的演化[1-2],同时岩石破碎亦是能量释放和耗散综合作用的结果,即能量释放直接导致岩石宏观破坏,而能量耗散则致使岩石发生塑性变形或损伤劣化。
近年来,岩石在各行业的需求量呈现出日益增多趋势。但是,岩石破碎过程的单位破碎能耗过高,导致能量消耗巨大。据国家统计局数据,破碎、磨矿作业消耗的能量可达全国总能源消耗的1.15%以上,然而破碎过程中能量利用效率较低,在矿石破碎中约为3%~5%[3-4]。近些年国家大力实施能耗“双控”管理,提出持续提高能源利用效率、不断提高绿色发展水平的目标。因此,开展岩石高效破碎理论与技术研究具有重要意义。
在岩石破碎过程中,外部加载方式是影响岩石力学特性与破裂行为的重要因素。在工业中常采用机械力破碎,加载方式主要为挤压、劈裂、折断、研磨、冲击及振动等[5],其中振动、冲击是最常用的加载方式,如锤式破碎机、振动破碎机、反击式破碎机等。国内外许多学者针对岩石的振动、冲击加载方式进行了大量探索。有的学者采用应力波的冲击加载方式,常见的实验设备是Hopkinson压杆。例如,Wang等[6]采用分离式Hopkinson压杆,研究了煤在反复冲击载荷作用下的破坏模式和断裂机理;李成杰等[7]采用分离式Hopkinson压杆,分析了煤、岩单体及组合体试件的能量耗散与破碎特征。有的学者采用机械冲击加载破碎试验方法,常用的设备为落锤冲击实验机。例如,Gan等[8]采用落锤冲击实验机对不规则磁铁矿进行单颗粒破碎试验,研究了矿石的形状和尺寸对破碎能量的影响;周强等[9]采用落锤冲击实验机对无烟煤和矸石进行破碎试验,研究了不同冲击比能下煤岩颗粒破碎的分形演化规律。随着现代科技的不断融入,许多新型测试设备也应用到各种科研活动中。例如,Zhang等[10]研究了超声振动激励下脆性红砂岩的断裂特性及能量耗散;尹崧宇[11]采用超声波振动破碎岩石装置,研究了超声振动下花岗岩的开裂条件、裂纹扩展特性等。
综上所述,目前已有的研究在岩石的强度特性、变形特征、能量演化等方面取得了富有成效的进展,但主要集中于单一加载方式,即只有岩石振动或冲击加载,鲜有研究涉及振动载荷对岩石冲击过程中破裂特征的影响,尤其缺少定量表征。目前在实际工程应用中,岩石冲击破碎过程也往往伴随着振动作用。例如,选矿工业中常见的惯性圆锥破碎机。同时,受限于目前的实验设备和测试手段,关于岩石破裂过程的研究主要关注宏观破坏特征及能量耗散特征,无法真正揭示岩石细观层面的力学特征,而细观层面的力学特征往往是宏观层面现象的内在原因。除此之外,能量利用效率是影响岩石损伤劣化效果的主要因素,而目前对于岩石破裂过程中断裂能采用间接计算方法获得[12-13],由于忽略了岩石破裂过程中产生的热能、声能、电磁辐射能、摩擦能及阻尼能等各种耗散能,计算结果误差较大。综上可知,研究振动载荷对青砂岩冲击裂纹扩展及能量利用效率的影响,既能全面适应现代化矿山建设与高效、节能、绿色生产的需求,亦具有重要的学术价值。
由于岩石受外部荷载作用发生破裂是一个连续介质离散化的过程,目前常规的数值模拟方法(有限单元法、有限差分法、块体离散单元法等)在分析岩石破裂问题时均带有局限性,而颗粒流离散元法可以分析岩石材料从线弹性阶段至断裂破坏的大变形过程,模拟裂纹的萌生、扩展及贯通过程,有效处理非连续介质力学问题[14],可以更加准确地研究岩石各种破碎行为。此外,利用颗粒流程序(particle flow code,PFC) 的颗粒黏结模型研究岩石细观力学响应已经得到了国际岩石力学界的普遍认同[15]。鉴于此,本文以岩石破碎作业中常见的准脆性物料——青砂岩为研究对象,采用颗粒流程序的平行黏结模型,通过冲击、振动冲击复合两种加载方式对青砂岩在破坏过程中裂纹扩展、能量利用效率进行对比分析。该研究不仅初步探索了振动载荷对青砂岩冲击裂纹扩展及能量利用效率的影响,还可为岩石破碎工艺参数的合理选择提供参考。
1 试验材料及参数标定 1.1 试验材料试验所采用的青砂岩岩样取自四川省自贡市,主要含硅、钙、黏土和氧化铁,是典型的脆性材料。为减小岩样离散性及节理特性对试验结果的影响,选取同一块岩石制作试件,沿垂直层理密集布孔钻取岩芯,加工成直径为50 mm、长度为100 mm的标准试件,平均密度为2.294 g/mm3。试件两端面的平行度、垂直度均控制在±0.02 mm以内,加工后的试件如图 1所示。采用中国科学院武汉岩土力学研究所研制的RMT-150B岩石力学实验系统分别进行单轴与假三轴压缩试验,得到青砂岩试件力学参数测试结果,如表 1所示。

|
| 图 1 青砂岩试件 |
1.2 本构模型
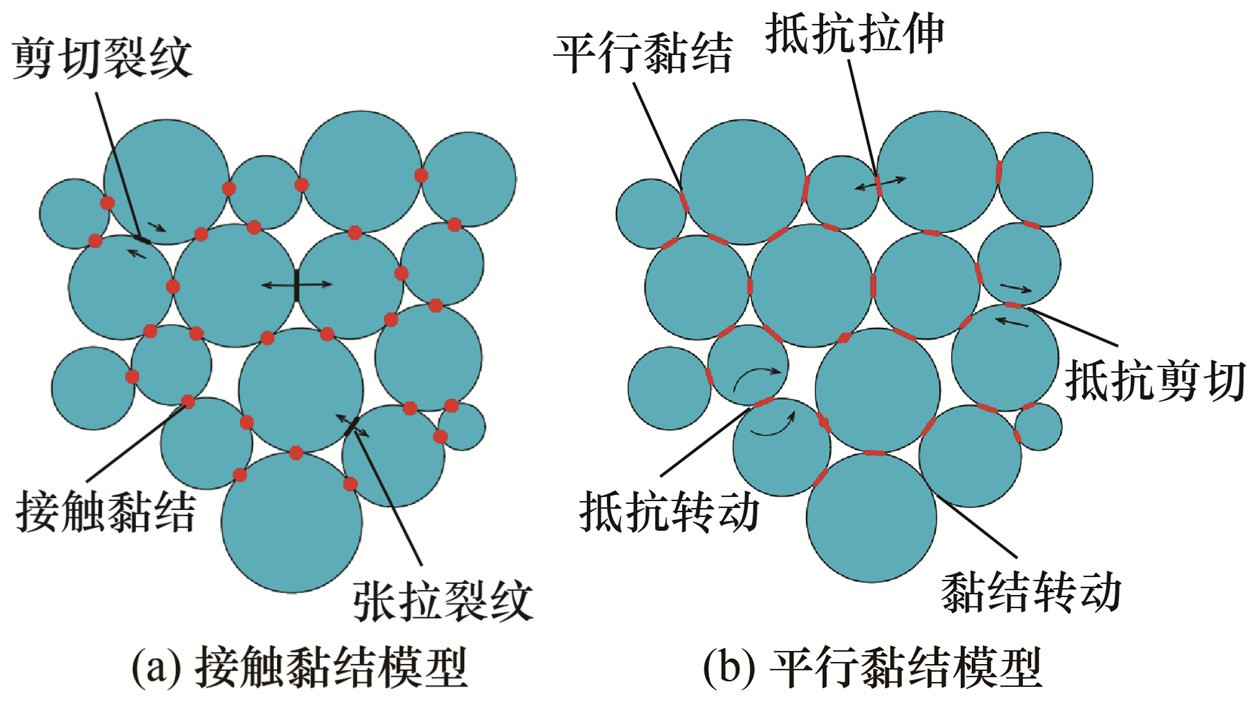
离散单元法克服了传统宏观连续性假设的局限性,可从细观角度研究岩石材料的宏观力学行为,建立岩石材料细观-宏观特征之间的关系[16]。颗粒流程序属于离散单元法,通过定义颗粒间的黏结接触模型,使颗粒间产生相互作用力,来模拟岩石的力学性质。黏结颗粒的接触方式如图 2[17]所示。接触黏结方式中,颗粒间通过一点发生接触,仅能传递力矢量;平行黏结方式中,颗粒间的接触方式是面接触,可同时实现力和力矩矢量的传递。相比而言,平行黏结方式更适合模拟岩石等脆性介质[17]。因此,本文青砂岩颗粒接触本构模型采用了平行黏结模型[18],如图 3[13]所示。图中:kn为法向刚度,ks为切向刚度,kn为平行黏结法向刚度,ks为平行黏结切向刚度,μ为颗粒摩擦系数,c为平行黏结切向强度,ϕ为摩擦角,gs为颗粒接触黏结间隙,σn为平行黏结法向强度。
1.3 细观参数标定
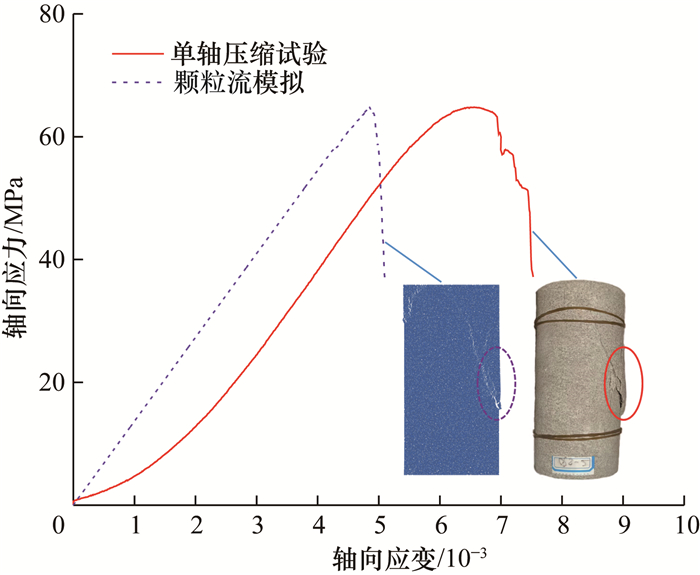
颗粒流程序采用细观力学参数表征颗粒及黏结的力学性质,细观参数决定着颗粒材料的宏观力学响应[19],因此细观参数选取的正确性与合理性是反映材料真实力学特性的基本前提。根据青砂岩试件的单轴抗压强度、弹性模量及Poisson比等宏观参数,采用“试错法”[20],经多次赋值,得到青砂岩试件的平行黏结模型细观参数标定结果(表 2)以及室内试验与参数标定结果对比(表 3)。由表 3可知,参数标定所得青砂岩试件单轴抗压峰值强度与室内试验结果相对差为0.082%,小于文[21]中0.840%、文[13] 中0.220%;弹性模量与室内试验结果相对差为0.724%,小于文[21]中的1.800%、文[13]中1.900%;Poisson比与室内试验结果相对差为0.284%。可见,参数标定结果与室内试验所得的青砂岩应力-应变曲线与破坏特征呈现出较好的一致性[22](图 4),因此本文青砂岩颗粒流模拟的细观参数设置具有合理性。
| 有效模量/GPa | 刚度比 | 平行黏结有效模量/GPa | 平行黏结刚度比 | 法向黏结强度/MPa | 切向黏结强度/MPa | 接触黏结间隙/mm | 摩擦角/ (°) | 阻尼系数 | 摩擦系数 |
| 7.580 | 3.600 | 7.580 | 3.600 | 30.200 | 19.084 | 0.050 | 37.700 | 0.700 | 0.300 |
| 数据类型 | 峰值强度/MPa | 弹性模量/GPa | Poisson比 |
| 室内试验 | 64.772 | 13.536 | 0.352 |
| 参数标定 | 64.825 | 13.634 | 0.353 |
| 相对差/% | 0.082 | 0.724 | 0.284 |
2 模拟方案
本文基于惯性圆锥破碎机在冲击加载、振动冲击复合加载方式下建立颗粒流数值模型。该破碎机主要依靠强烈振动产生的简谐振动力和可调节的冲击力,对各种岩石进行选择性破碎,相较于其他破碎方式,具有能耗较低、破碎力大、破碎机比大、产品粒度细且均匀等优点[5]。此外,在实际工业生产应用过程中,由于破碎岩石存在大小差异性及形状不规则性,不利于颗粒流分析。因此,本文简化青砂岩为规则形状,建立与室内试验试件尺寸相同的二维颗粒流计算模型,尺寸为50 mm(直径)×100 mm(高度)。冲击试块采用钢块,材质为Q235-A,尺寸为70 mm(直径)×20 mm(高度)。青砂岩冲击力与振动作用力受载长度均为50 mm。
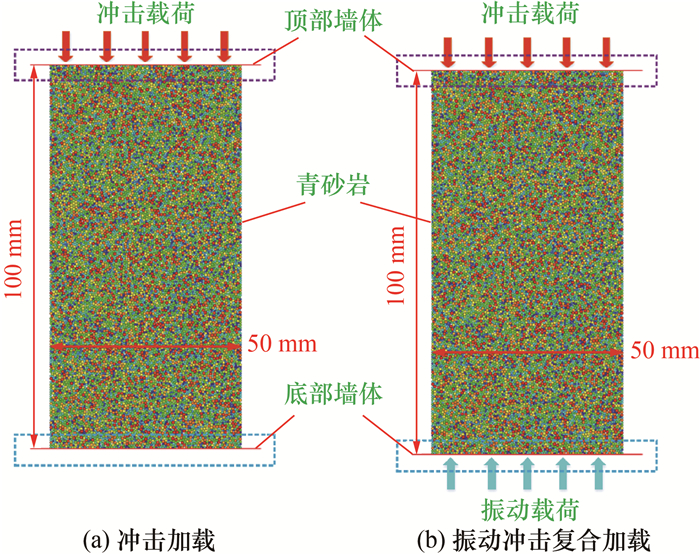
根据实际破碎工况,在青砂岩模型建立后,删除两侧约束,保留顶部和底部边界墙体约束。模型边界条件及载荷施加区域如图 5所示。在冲击加载方式下(图 5a),利用内嵌的FISH语言编写程序对青砂岩模型载荷区域的顶部墙体施加不同加载速度的冲击载荷,对底部墙体进行固定设置;在振动冲击复合加载方式下(图 5b),利用内嵌的FISH语言编写程序对青砂岩模型载荷区域的顶部墙体施加不同加载速度的冲击载荷,对底部墙体施加不同振幅与振动频率的振动载荷。
|
| 图 5 青砂岩模型边界条件及载荷施加示意 |
青砂岩模拟方案主要分为两种加载方式(表 4):
| 加载方式 | 冲击速度/(m·s-1) | 振幅/mm | 振动频率/Hz | ||||||||||||
| 10 | 15 | 20 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 5 | 10 | 15 | 20 | 25 | |||
| 冲击加载 |  |
||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
| 振动冲击复合加载 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||||
注: 与 与 采用正交方法组合。 采用正交方法组合。 |
|||||||||||||||
1) 冲击加载。冲击试块以不同的冲击速度冲击青砂岩试件,接触瞬时速度分别为10、15、20 m/s,冲击加载时间设置为0.1 ms。
2) 振动冲击复合加载。冲击试块以不同的冲击速度冲击青砂岩试件,接触瞬时速度分别为10、15、20 m/s,同时青砂岩底部进行振动加载,振幅分别设置为0.5、1、1.5、2、2.5 mm,每个振幅分别设置振动频率为5、10、15、20、25 Hz,振动冲击复合加载时间设置为0.1 ms。
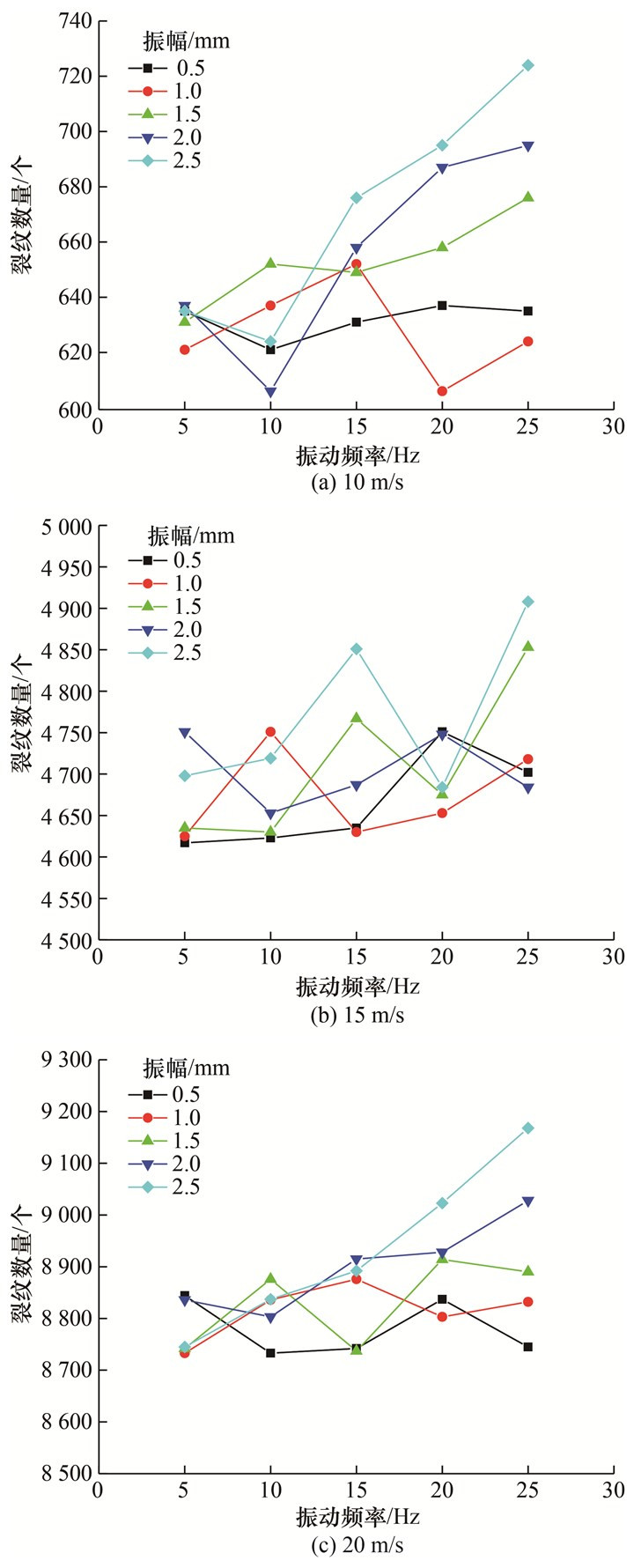
3 结果与分析 3.1 裂纹扩展规律在岩石损伤劣化过程中,岩石内部产生的宏观裂纹是由微观裂纹不断萌生、延伸、相互贯通所导致的,因此裂纹数量是衡量破裂效果的一个重要指标。振动冲击复合作用下,冲击速度为10、15、20 m/s,振动频率为5、10、15、20、25 Hz,振幅为0.5、1.0、1.5、2.0、2.5 mm时,青砂岩裂纹数量统计如图 6所示。
|
| 图 6 不同冲击速度下青砂岩裂纹数量 |
1) 随着冲击速度的增加,青砂岩裂纹数量显著增加。例如,在振动频率为25 Hz、振幅为2.5 mm条件下,冲击速度为10 m/s时,青砂岩的裂纹数量为724个;在冲击速度为15、20 m/s时,裂纹数量分别为4 908、9 168个,增幅分别为577.9%、1 166.3%。
2) 在相同的冲击速度、振幅作用下,改变振动频率,青砂岩的裂纹数量表现出上下波动现象,但总体上裂纹数量呈现出增大趋势,但增幅相对较小。例如,在冲击速度为20 m/s、振幅为2.5 mm条件下,振动频率为5 Hz时,青砂岩的裂纹数量为8 745个;而在振动频率分别为10、15、20、25 Hz时,裂纹数量分别为8 837、8 892、9 023、9 168个,增幅分别为1.1%、1.7%、3.2%、4.8%。
3) 在相同的冲击速度、振动频率下,改变振幅,青砂岩在振动频率较低时,裂纹较为集中,而随着振动频率增大,裂纹表现出分散现象,但总体上裂纹数量呈现出增大趋势,增幅较小。例如,在冲击速度为20 m/s、振动频率为25 Hz条件下,振幅为0.5 mm时,青砂岩的裂纹数量为8 745个;而在振幅分别为1.0、1.5、2.0、2.5 mm时,裂纹数量分别为8 832、8 890、9 028、9 168个,增幅分别为1.0%、1.7%、3.2%、4.8%。
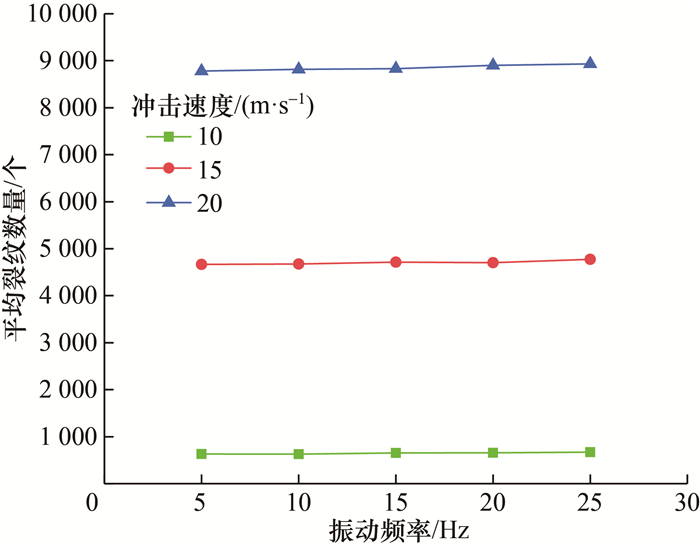
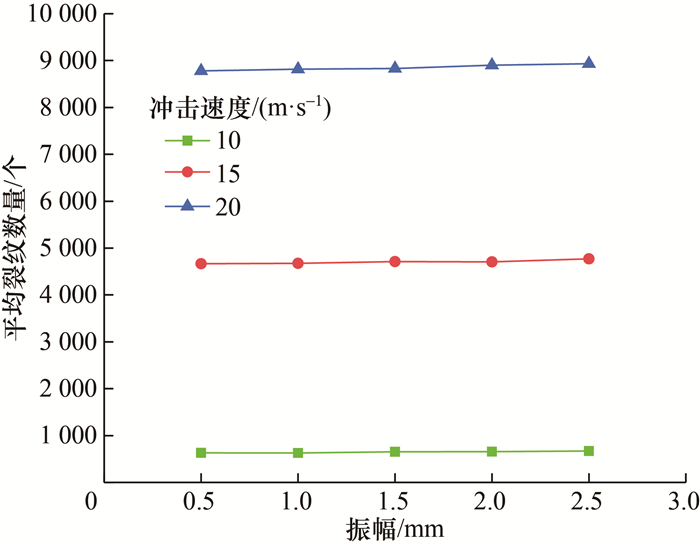
对图 6中不同冲击速度下青砂岩裂纹数量的数据进行统计处理,得出冲击速度为10、15、20 m/s时,不同振动频率、振幅作用下青砂岩平均裂纹数量分别如图 7、8所示。
|
| 图 7 不同振动频率下青砂岩平均裂纹数量 |
|
| 图 8 不同振幅下青砂岩平均裂纹数量 |
1) 不同振动频率和振幅下青砂岩平均裂纹数量相似,呈近乎直线形状,但随着冲击速度的增大,平均裂纹数量明显增大。例如,在振动频率为15 Hz、冲击速度为10 m/s时,青砂岩的平均裂纹数量为653个;而在冲击速度为15、20 m/s时,平均裂纹数量分别为4 714、8 832个,增幅分别为621.7%、1 252.2%,表明冲击速度对裂纹数量的影响远大于振动加载。
2) 振动频率分别为5、10、15、20、25 Hz,与振幅分别为0.5、1.0、1.5、2.0、2.5 mm时,平均裂纹数量差异较小,主要原因是在此振动频率与振幅作用下,破碎机对青砂岩底部产生的振动冲击力相差较小。
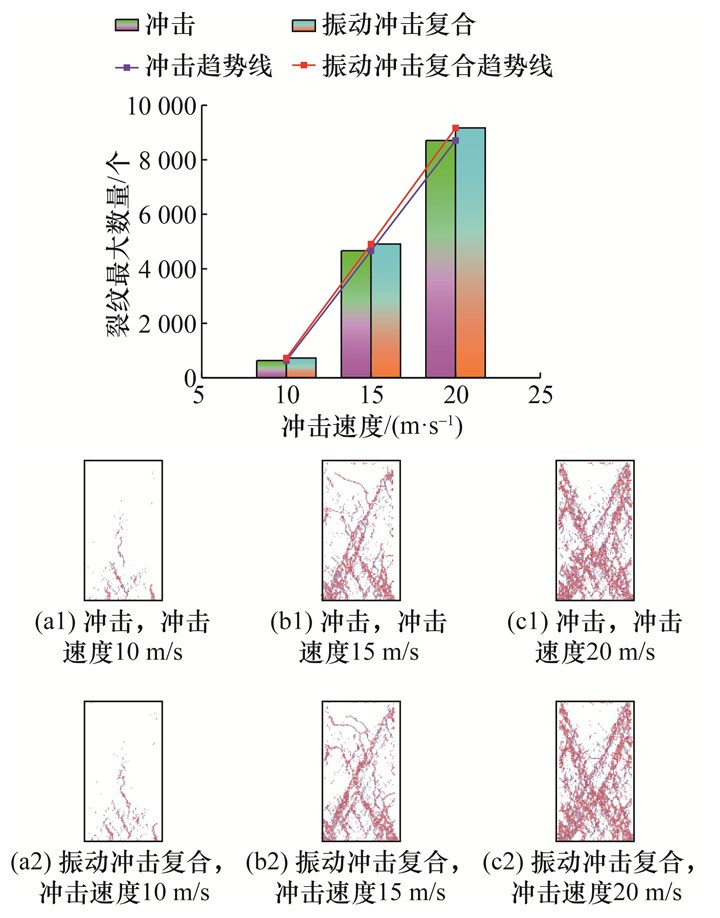
为进一步分析振动载荷对青砂岩裂纹数量的影响,冲击、振动冲击复合作用下裂纹最大数量和裂纹分布特点对比如图 9所示,其中裂纹分布特点中,红色、浅紫色分别表示拉伸裂纹、剪切裂纹。
|
| 图 9 不同加载方式下青砂岩裂纹最大数量和裂纹分布特点对比 |
1) 冲击、振动冲击复合作用下,青砂岩裂纹最大数量均呈接近直线形增加趋势,但振动冲击复合作用下裂纹最大数量增长速度明显大于冲击作用。在相同的冲击速度下,与冲击作用相比,振动冲击复合作用下的裂纹最大数量增幅逐渐变小,在冲击速度分别为10、15、20 m/s时,振动冲击复合裂纹最大数量的增幅分别为14.557%、5.322%、5.282%。
2) 在青砂岩的破裂过程中,微观裂纹破坏表现为颗粒间黏结键的断裂,可分为拉伸型断裂和剪切型断裂,进而表现出拉伸型微裂纹和剪切型微裂纹。冲击、振动冲击复合作用下,裂纹分布极为相似,由青砂岩下部向上端与两侧延伸,最后裂纹呈X状共轭斜面断裂特征,同时拉伸裂纹的数量多于剪切裂纹,说明拉伸裂纹在青砂岩的最终破坏过程中起主要作用,这与文[13]对于裂纹数量演化特征的研究结果一致。
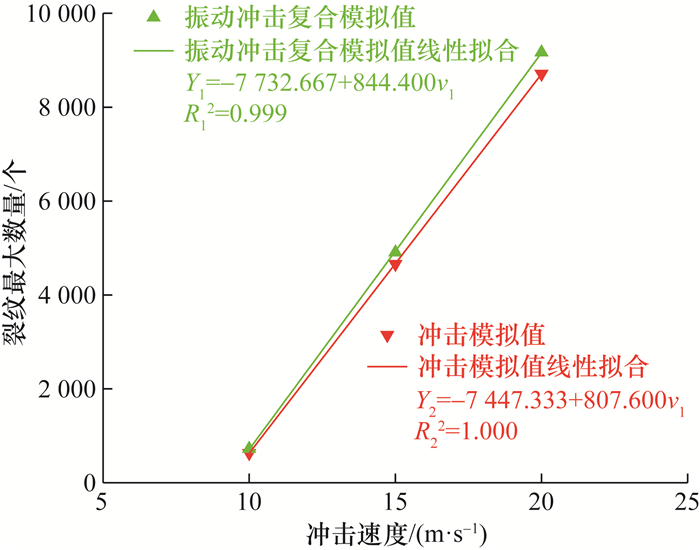
对冲击、振动冲击复合作用下青砂岩裂纹最大数量的模拟值进行线性拟合,得到图 10所示的拟合线。可见,冲击、振动冲击复合作用下裂纹最大数量与冲击速度近似符合直线关系,且振动冲击复合作用下的斜率明显大于冲击作用,说明在振动冲击复合作用下,振动载荷对于青砂岩裂纹数量的增加起到一定辅助作用,裂纹最大数量的增加量与冲击速度的关系可以表示为
| $ \Delta Y=Y_1-Y_2=-285.334+364.800 v_1 . $ | (1) |
|
| 图 10 青砂岩裂纹最大数量线性拟合 |
其中:v1为冲击速度,Y1、Y2分别为振动冲击复合、冲击作用下的裂纹最大数量。
3.2 能量利用效率断裂能是岩石破裂过程中用于裂纹生成最有效的能量,而能量利用效率对于节能降耗具有重要意义。青砂岩在冲击、振动冲击复合加载作用下,主要输入能量来自于冲击载荷和振动载荷,而颗粒之间的黏结键断裂所消耗的能量为断裂能,其具体计算过程如下:
1) 冲击输入能量。
冲击输入能量主要取决于冲击试块质量与冲击速度,
| $ E_1=\frac{1}{2} m_1 v_1^2 . $ | (2) |
其中m1为冲击试块质量,取值为10.990 kg。
2) 振动输入能量。
设定青砂岩试件速度为简谐振动的最大速度。青砂岩试件底部在振动冲击瞬间的位移为
| $ x=A \sin \omega t . $ | (3) |
其中:A为振幅,ω为角速度,t为时间。
振动过程中,振动速度为
| $ v_2=\dot{x}=A \omega \cos \omega t . $ | (4) |
在冲击时间0 ~ t内,振动冲击复合作用下总输入能量为
| $ \begin{gathered} E_2=F \cdot \mathrm{~d} x=m_2 \frac{\mathrm{~d} v_2}{\mathrm{~d} t} \cdot \mathrm{~d} x= \\ \int_0^t\left[\frac{1}{2} m_2 A^2 \omega^3 \sin 2 \omega t\right] \mathrm{d} t= \\ -\left.\frac{1}{4} m_2 A^2 \omega^2 \cdot \cos 2 \omega t\right|_0 ^t= \\ \frac{1}{4} m_2 A^2 \omega^2(1-\cos 2 \omega t). \end{gathered} $ | (5) |
其中:F为青砂岩试件振动作用力;m2为青砂岩试件质量,取值为11.470 kg。
3) 能量利用效率。
在青砂岩颗粒流模拟中,颗粒之间的有效黏结可以阻止相对切向和法向运动,其中法向平行黏结力Fn、切向平行黏结力Fs和法向平行黏结力矩Tn、切向平行黏结力矩 Ts,按式(6)随着时间的增加而变化[23]。
| $ \left\{\begin{array}{l} {\rm{ \mathsf{ δ}}} \bar{F}_n=-v_n \bar{k}_n \bar{A} {\rm{ \mathsf{ δ}}} t ; \\ {\rm{ \mathsf{ δ}}} \overline{\boldsymbol{F}}_s=-\boldsymbol{v}_s \bar{k}_s \bar{A} {\rm{ \mathsf{ δ}}} t ; \\ {\rm{ \mathsf{ δ}}} \bar{T}_n=-\omega_n \bar{k}_s \bar{J} {\rm{ \mathsf{ δ}}} t ; \\ {\rm{ \mathsf{ δ}}} \overline{\boldsymbol{T}}_s=-\frac{1}{2} \boldsymbol{\omega}_s \bar{k}_n \bar{J} {\rm{ \mathsf{ δ}}} t . \end{array}\right. $ | (6) |
其中:A为平行黏结键的横截面积,J为平行黏结键截面的极性惯性矩,vn和vs分别为破碎颗粒的法向速度和切向速度,ωn和ωs分别为切向角速度和法向角速度,δt为时步。
青砂岩颗粒之间的平行黏结键在颗粒接触区域的黏结间隙范围之内传递力与力矩。限制总法向力、切向力使青砂岩颗粒在黏结强度范围内发生接触。当最大法向应力或者最大切向应力超过了青砂岩的法向黏结强度δmax与切向黏结强度τmax时,颗粒之间的平行黏结键就会被破坏[24],即
| $ \left\{\begin{array}{l} \delta_{\max }<\frac{\bar{F}_n}{\bar{A}}+\bar{\beta} \frac{\left\|\overline{\boldsymbol{M}}_{\mathrm{b}}\right\| \bar{R}}{\bar{I}} ; \\ \tau_{\max }<\frac{\left\|\overline{\boldsymbol{F}}_s\right\|}{\bar{A}}+\bar{\beta} \frac{\left|\bar{M}_{\mathrm{t}}\right| \bar{R}}{\bar{J}} . \end{array}\right. $ | (7) |
其中:R为平行黏结半径,I为平行黏结键横截面的惯性矩,Mb为平行黏结键扭矩,Mt为平行黏结键力矩,β为力矩贡献因子。
此时平行黏结键断裂所消耗的能量即为青砂岩在外部加载下破碎时的黏结破坏能,也称为断裂能[13-14],其计算公式为
| $ E_{\mathrm{d}}=\frac{1}{2}\left[\frac{\bar{F}_n^2}{\bar{k}_n \bar{A}}+\frac{\left\|\overline{\boldsymbol{F}}_s\right\|^2}{\bar{k}_s \bar{A}}+\frac{\bar{M}_{\mathrm{t}}^2}{\bar{k}_s \bar{J}}+\frac{\left\|\overline{\boldsymbol{M}}_{\mathrm{b}}\right\|^2}{\bar{k}_n \bar{I}}\right] . $ | (8) |
由式(2)和(5)可得出振动输入能量占比,
| $ \lambda=\frac{E_2}{E_1+E_2}=\frac{m_2 A^2 \omega^2(1-\cos 2 \omega t)}{2 m_1 v_1^2+m_2 A^2 \omega^2(1-\cos 2 \omega t)} . $ | (9) |
由式(8)得出冲击、振动冲击复合作用下的断裂能分别为Ed1、Ed2,结合式(2)、(5)得出冲击、振动冲击复合作用下能量利用效率η1、η2分别为:
| $ \eta_1=\frac{E_{\mathrm{d} 1}}{E_1}=\frac{2 E_{\mathrm{dl}}}{m_1 v_1{ }^2} . $ | (10) |
| $ \eta_2=\frac{E_{\mathrm{d} 2}}{E_1+E_2}=\frac{4 E_{\mathrm{d} 2}}{2 m_1 v_1^2+m_2 A^2 \omega^2(1-\cos 2 \omega t)} . $ | (11) |
由式(10)与(11)得到振动载荷对冲击破坏过程中能量利用效率增幅γ为
| $ \begin{gathered} \gamma=\frac{\eta_2-\eta_1}{\eta_1}= \\ \frac{2 m_1 v_1^2\left(E_{\mathrm{d} 2}-E_{\mathrm{d} 1}\right)-2 E_{\mathrm{d} 1} m_2 A^2 \omega^2(1-\cos 2 \omega t)}{E_{\mathrm{d} 1}\left[2 m_1 v_1^2+m_2 A^2 \omega^2(1-\cos 2 \omega t)\right]} . \end{gathered} $ | (12) |
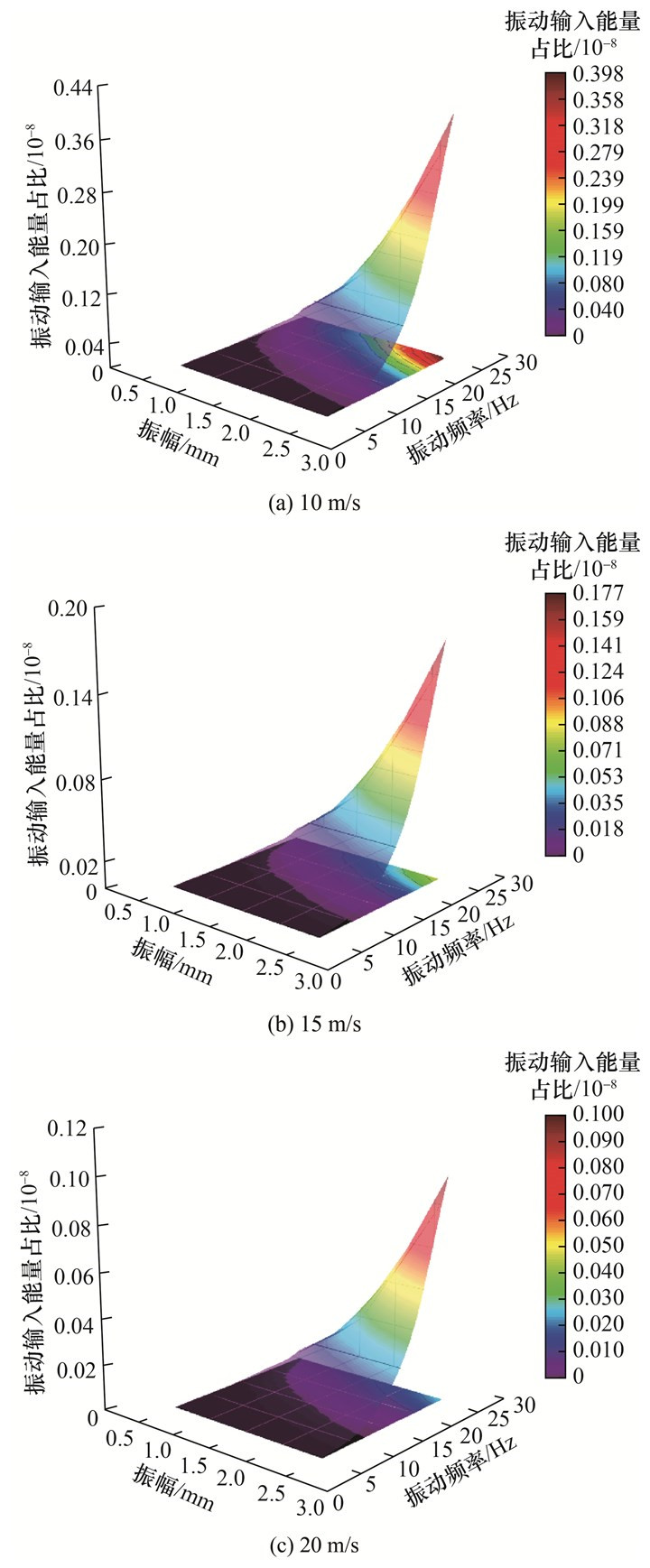
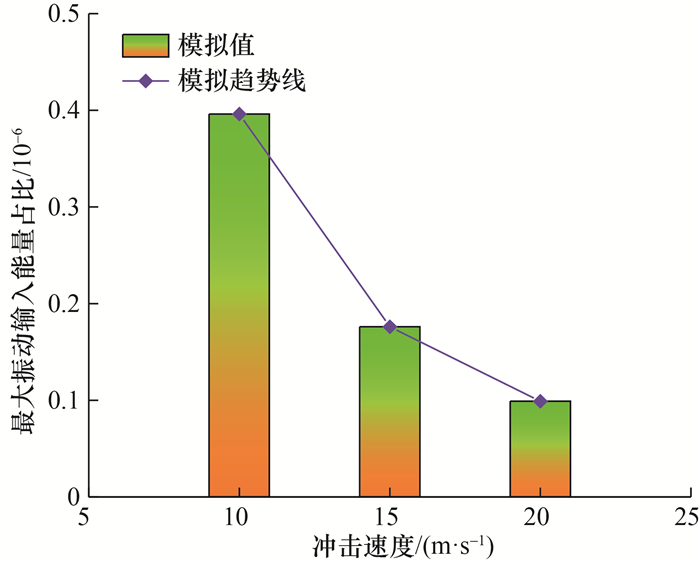
根据式(9)得出青砂岩振动输入能量占比,结果如图 11所示。在相同冲击速度下,随着振动频率与振幅的增加,青砂岩振动输入能量占比呈现出增加趋势,但随着冲击速度的增加,青砂岩振动输入能量在总输入能量中的占比呈现出下降趋势。不同冲击速度下青砂岩最大振动输入能量占比如图 12所示。随着冲击速度的增加,青砂岩最大振动输入能量占比减小,这是由于青砂岩振动输入能量较小,而随着冲击速度的增加,冲击输入能量的增幅远远大于振动输入能量的增幅。
|
| 图 11 不同冲击速度下青砂岩振动输入能量占比 |
|
| 图 12 不同冲击速度下青砂岩最大振动输入能量占比 |
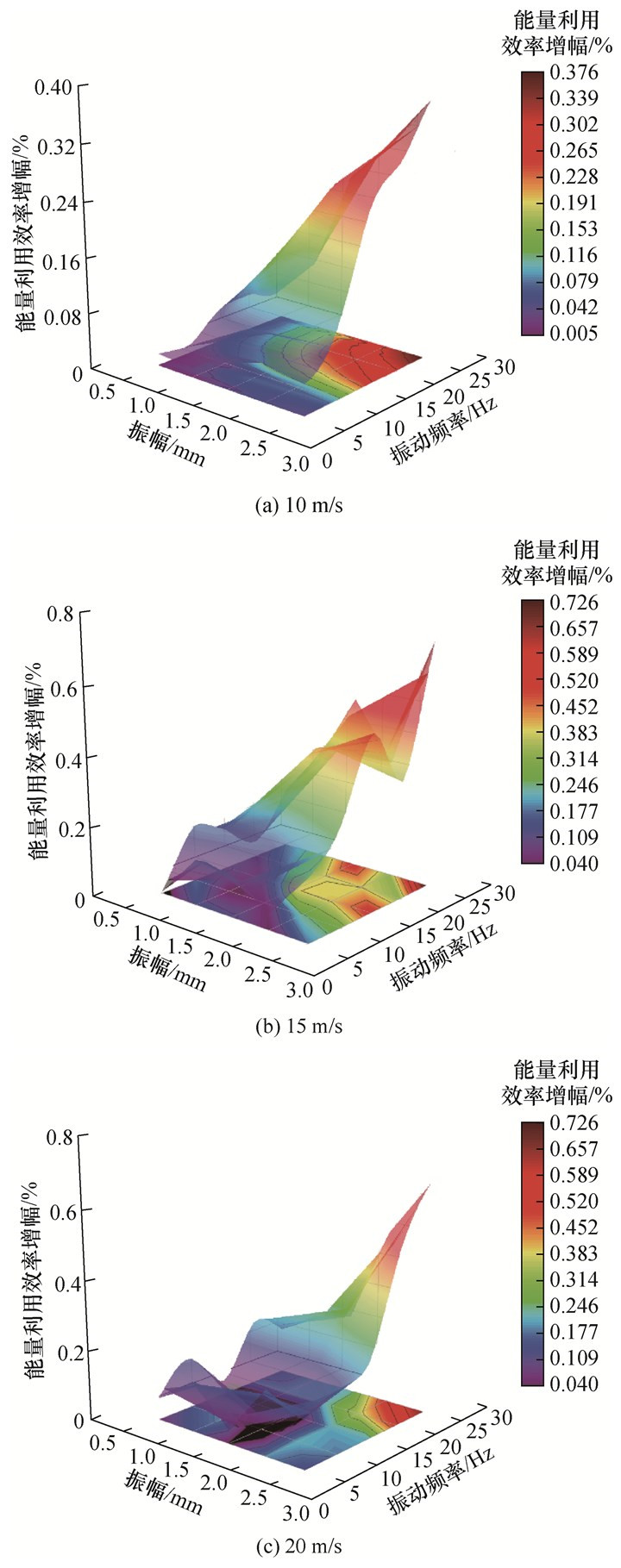
根据式(12),通过对冲击、振动冲击复合作用下青砂岩能量利用效率进行对比,得出青砂岩能量利用效率增幅,如图 13所示。在相同冲击速度下,随着振动频率和振幅增加,振动冲击复合作用下能量利用效率的增幅存在波动现象。
|
| 图 13 不同冲击速度下青砂岩能量利用效率增幅 |
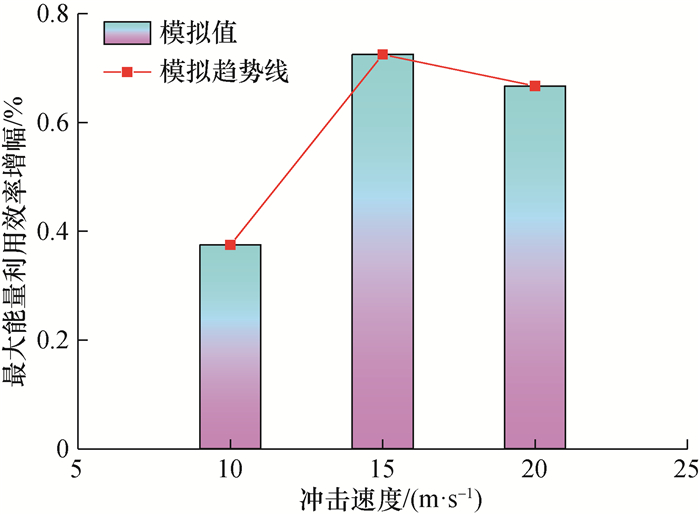
不同冲击速度下青砂岩最大能量利用效率增幅如图 14所示。随着冲击速度的增加,最大能量利用效率增幅呈现出先增加而后降低的趋势。这是由于从能量角度看,在外部载荷作用下青砂岩的变形破坏为典型的物理变化,本质是将积聚的机械能转化为耗散能的动态过程。当冲击速度较小时,在振动激励下,青砂岩颗粒的振动使岩石颗粒之间产生更大的拉伸力,加速了颗粒黏结键的破坏,使输入能量以裂纹和损伤形式耗散,青砂岩内部微裂纹萌生、扩展和贯通破坏加剧。但是,随着冲击速度增大,输入能量逐渐以热能、声能、动能、电磁辐射能、摩擦能等形式向外界释放耗散,断裂能所占比例的增加相对较小,因此最大能量利用效率增幅呈现出下降趋势。
|
| 图 14 不同冲击速度下青砂岩最大能量利用效率增幅 |
综上可知,与冲击作用相比,在振动冲击复合作用下,由于振动输入能量占比小,相对而言,振动载荷(增加振动频率或振幅)能显著提高能量利用效率。当冲击速度为15 m/s时,最大振动输入能量占比为0.176×10-6,青砂岩最大能量利用效率增幅为0.725%。这也说明冲击作用对于能量利用效率的增幅起到主要作用,而振动载荷对于能量利用效率的增幅起到一定的辅助作用。因此,在实际岩石破碎工程应用中,适当增加振动载荷(振动频率或者振幅),在一定程度上有利于加剧岩石的损伤劣化,有助于以较低的能量输入显著提高岩石能量利用效率增幅,从而对破碎作业节能及降耗起到一定的辅助作用。
4 结论本文结合室内试验与细观参数标定,建立青砂岩宏-细观力学响应关系,对比分析了冲击、振动冲击复合加载下的裂纹扩展及能量利用效率。在参数标定过程中综合考虑了弹性模量、峰值强度及Poisson比等室内试验测试参数,保证了细观参数设置的合理性。本文研究了振动载荷对青砂岩裂纹数量扩展的影响,建立了振动载荷作用下裂纹增加数量与冲击速度的定量关系。结合理论分析与颗粒流模拟,通过编写FISH语言程序,采用直接计算方法,探索发现振动载荷对能量利用效率增幅的显著影响:在相同冲击速度作用下,增加振动频率或振幅,青砂岩裂纹数量与能量利用效率的增幅总体上均呈现出增大趋势。两种加载方式下,随冲击速度的增大,青砂岩裂纹最大数量均呈接近直线形增长,拉伸裂纹的数量居多,裂纹的分布均呈X状共轭斜面特征,但振动冲击复合加载下裂纹增长速度相对较大;振动载荷对最大能量利用效率的增幅呈现出先快速增加后减小的趋势,最大增幅为0.725%。
但本研究仍存在不足之处,比如岩石破裂时间较短(一般为μs级),而能量变化对环境反应较为敏感,在真实试验条件下难以实现相同的研究环境,且存在能量观测手段的诸多限制,虽然颗粒流模拟可以弥补室内试验难以获取裂纹动态扩展过程中断裂能的缺陷,但尚缺乏深入的试验验证,因此后续工作将结合物理试验、数值模拟与测试技术,从宏-细-微观多尺度探索岩石的破裂机制及能量演化特征。
| [1] |
谢和平, 彭瑞东, 鞠杨, 等. 岩石破坏的能量分析初探[J]. 岩石力学与工程学报, 2005, 24(15): 2603-2608. XIE H P, PENG R D, JU Y, et al. On energy analysis of rock failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2603-2608. (in Chinese) |
| [2] |
HOEK E, BIENIAWSKI Z T. Brittle fracture propagation in rock under compression[J]. International Journal of Fracture Mechanics, 1965, 1(3): 137-155. DOI:10.1007/BF00186851 |
| [3] |
YAHYAEI M, HILDEN M, SHI F, et al. Comminution[M]. Cham, Switzerland: Springer International Publishing, 2016.
|
| [4] |
ZHANG Z X, OUCHTERLONY F. Energy requirement for rock breakage in laboratory experiments and engineering operations: A review[J]. Rock Mechanics and Rock Engineering, 2022, 55(2): 629-667. DOI:10.1007/s00603-021-02687-6 |
| [5] |
夏晓鸥, 罗秀建. 惯性圆锥破碎机[M]. 北京: 冶金工业出版社, 2015. XIA X O, LUO X J. Inertia cone crusher[M]. Beijing: Metallurgical Industry Press, 2015. (in Chinese) |
| [6] |
WANG K, FENG G R, QI T Y, et al. Experimental investigation on dynamic mechanical characteristics and fracture mechanism of coal under repeated impact loads[J]. Arabian Journal of Geosciences, 2021, 14(14): 1311. DOI:10.1007/s12517-021-07680-5 |
| [7] |
李成杰, 徐颖, 叶洲元. 冲击荷载下类煤岩组合体能量耗散与破碎特性分析[J]. 岩土工程学报, 2020, 42(5): 981-988. LI C J, XU Y, YE Z Y. Energy dissipation and crushing characteristics of coal-rock-like combined body under impact loading[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 981-988. (in Chinese) |
| [8] |
GAN D Q, GAO F, ZHANG Y P, et al. Effects of the shape and size of irregular particles on specific breakage energy under drop weight impact[J]. Shock and Vibration, 2019, 2019: 2318571. DOI:10.1155/2019/2318571 |
| [9] |
周强, 潘永泰, 郭庆, 等. 不同冲击比能下煤岩颗粒破碎的分形演化[J]. 煤炭工程, 2020, 52(4): 143-148. ZHOU Q, PAN Y T, GUO Q, et al. Fractal evolution of particle fragmentation of ore and rock under different impact energy[J]. Coal Engineering, 2020, 52(4): 143-148. (in Chinese) |
| [10] |
ZHANG L, WANG X F, WANG J Y, et al. Research on fracture characteristics and energy dissipation of hard rock under the excitation of ultrasonic vibration[J]. Geofluids, 2022, 2022: 8351316. |
| [11] |
尹崧宇. 超声波振动下花岗岩裂纹变化特性的研究[D]. 长春: 吉林大学, 2017. YIN S Y. Research on the characteristics of granite crack variation under ultrasonic vibration[D]. Changchun: Jilin University, 2017. (in Chinese) |
| [12] |
GUO Q, PAN Y T, ZHOU Q, et al. Kinetic energy calculation in granite particles comminution considering movement characteristics and spatial distribution[J]. Minerals, 2021, 11(2): 217. DOI:10.3390/min11020217 |
| [13] |
张磊. 超声振动激励下坚硬岩石高效破碎基础研究[D]. 徐州: 中国矿业大学, 2021. ZHANG L. Basic research on high efficient crushing of hard rock under ultrasonic vibration excitation[D]. Xuzhou: China University of Mining and Technology, 2021. (in Chinese) |
| [14] |
石崇, 张强, 王盛年. 颗粒流(PFC5.0)数值模拟技术及应用[M]. 北京: 中国建筑工业出版社, 2018. SHI C, ZHANG Q, WANG S N. Numerical simulation technology and application with particle flow code (PFC5.0)[M]. Beijing: China Architecture & Building Press, 2018. (in Chinese) |
| [15] |
POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364. DOI:10.1016/j.ijrmms.2004.09.011 |
| [16] |
阿比尔的, 郑颖人, 冯夏庭, 等. 平行黏结模型宏细观力学参数相关性研究[J]. 岩土力学, 2018, 39(4): 1289-1301. ERDI A, ZHENG Y R, FENG X T, et al. Relationship between particle micro and macro mechanical parameters of parallel-bond model[J]. Rock and Soil Mechanics, 2018, 39(4): 1289-1301. (in Chinese) |
| [17] |
程爱平, 舒鹏飞, 邓代强, 等. 单轴压缩下尾砂胶结充填体细观能量耗散与损伤表征研究[J]. 采矿与安全工程学报, 2022, 39(6): 1227-1234. CHENG A P, SHU P F, DENG D Q, et al. Study on mesoscale energy dissipation and damage characterization of cemented tailings backfill under uniaxial compression[J]. Journal of Mining & Safety Engineering, 2022, 39(6): 1227-1234. (in Chinese) |
| [18] |
徐小敏, 凌道盛, 陈云敏, 等. 基于线性接触模型的颗粒材料细-宏观弹性常数相关关系研究[J]. 岩土工程学报, 2010, 32(7): 991-998. XU X M, LING D S, CHEN Y M, et al. Correlation of microscopic and macroscopic elastic constants of granular materials based on linear contact model[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 991-998. (in Chinese) |
| [19] |
佟安, 张军徽, 武娜. 红砂岩单轴压缩宏细观参数映射关系研究[J]. 力学与实践, 2020, 42(2): 202-208. TONG A, ZHANG J H, WU N. Macro and microscopic parameter mapping relationship for red sandstone[J]. Mechanics in Engineering, 2020, 42(2): 202-208. (in Chinese) |
| [20] |
龚囱, 包涵, 王文杰, 等. 红砂岩破坏过程声发射震源演化规律及其主频特征[J]. 煤炭学报, 2022, 47(6): 2326-2339. GONG C, BAO H, WANG W J, et al. Evolution law and dominant frequency characteristics of acoustic emission sources during red sandstone failure process[J]. Journal of China Coal Society, 2022, 47(6): 2326-2339. (in Chinese) |
| [21] |
于利强, 姚强岭, 徐强, 等. 加载速率影响下裂隙细砂岩裂纹扩展试验及数值模拟研究[J]. 煤炭学报, 2021, 46(11): 3488-3501. YU L Q, YAO Q L, XU Q, et al. Experimental and numerical simulation study on crack propagation of fractured fine sandstone under the influence of loading rate[J]. Journal of China Coal Society, 2021, 46(11): 3488-3501. (in Chinese) |
| [22] |
赵环帅, 潘永泰, 余超, 等. 锤式破碎机冲击速率对青砂岩破碎效果及能量利用效率的影响[J/OL]. 煤炭科学技术, 2024: 1-13. [2024-04-15]. http://kns.cnki.net/kcms/detail/11.2402.TD.20240205.1820.005.html. ZHAO H S, PAN Y T, YU C, et al. The influence of impact velocities of hammer crusher on the crushing effect and utilization efficiency of fracture energy in green sandstone[J/OL]. Coal Science and Technology, 2024: 1-13. [2024-04-15]. http://kns.cnki.net/kcms/detail/11.2402.TD.20240205.1820.005.html. (in Chinese) |
| [23] |
丁桐桐, 徐建华, 李远安, 等. 基于离散单元法的立轴冲击破碎机成砂率数值计算[J]. 应用力学学报, 2021, 38(5): 2018-2024. DING T T, XU J H, LI Y A, et al. Numerical calculation of sand formation rate of vertical shaft impact crusher based on discrete element method[J]. Chinese Journal of Applied Mechanics, 2021, 38(5): 2018-2024. (in Chinese) |
| [24] |
LIN Z Y, WANG Y S, TANG C S, et al. Discrete element modelling of desiccation cracking in thin clay layer under different basal boundary conditions[J]. Computers and Geotechnics, 2021, 130: 103931. |