2. 清华大学 水圈科学与水利工程全国重点实验室, 北京 100084;
3. 清华大学 水利部水圈科学重点实验室, 北京 100084;
4. 北京科技大学 土木与资源工程学院, 北京 100083;
5. 北京科技大学 金属矿山高效开采与安全教育部重点实验室, 北京 100083
2. State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China;
3. Key Laboratory of Hydrosphere Sciences of the Ministry of Water Resources, Tsinghua University, Beijing 100084, China;
4. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China;
5. Key Laboratory of Ministry for Efficient Mining and Safety of Metal Mines, University of Science and Technology Beijing, Beijing 100083, China
深部煤层开采面临着与浅部开采不同的“三高一扰动”复杂环境属性,各种地质灾害呈现突变性、复杂性及破坏性高的态势[1-3]。传统方法监测困难且解围措施控制效果不佳,严重制约了煤炭资源的安全高效开采[4-5]。相关研究表明[6-9]:深部动力灾害频发与地应力场的复杂性分布密切相关,特别是在含隐伏断层带的深部采场区域,断层受开采扰动影响而活化并释放能量是诱发冲击地压及矿震的主要因素,且地应力状态与断层滑移失稳密切相关。因此,阐明深部非连续区域的地应力分布规律对于工程防灾减灾工程至关重要。现场实测是获得地应力资料最直接的方法,但工程地质条件及高昂造价的限制,无法大规模开展测量[5, 10-11]。且深部岩体处于“三高”的赋存环境中,地应力场具有显著的非线性与非连续性特征,使测量结果离散且数据有效利用率降低[12]。因此,根据现场地应力测点数据,充分考虑深部地质特性,采用基于数值仿真的数据驱动的方法反演地应力场已成为学者们研究的重点。
在含隐伏断层区域地应力场分布规律的研究方面,学者们取得了丰硕的成果。陈世杰等[13]定性分析断层对地应力场方向的影响规律,分别建立金川矿区地下厂房大尺度连续分布地质模型及小尺度含断裂构造的精细化模型,并采用等效构造作用载荷的二次反演分析方法,获得了精细模型反演结果并全面解释了区域实测主应力异常现象。裴启涛等[14]以断层、节理等非线性构造显著的乌东德水电站区域的地层为研究背景,采用有限差分与离散元相结合的方法,对地应力场进行多尺度反演。陈爽等[15]建立了考虑断层及破碎带影响的地应力场反演方法,对断层带施加挤压力和压扭力以模拟断层错动机实现局部应力场调整,从而明显提高了反演精度。寇昊等[16]提出了考虑走滑断裂活动影响的公路隧道初始地应力场反演方法,采用位移载荷对模拟断裂带两侧岩体的相对挤压及滑动作用,获得了符合跨断层岩体区域的地应力场分布规律。吕进国等[17]对沿断层不同方向的开采工况进行了数值模拟,揭示了开采扰动对断层面上的法向应力和切向应力影响规律。
虽然上述方法对断层局部区域的地应力场分布规律进行了有效的解析,但无法反演出整个断层等非连续构造区域的地应力场的分布特征。为此,本文提出了适用于深部煤层非连续区的地应力场的反演方法,考虑深部地质体的正断层、逆断层和走滑断层区域的地应力场稳定性分布规律,建立了基于地应力场侧压力系数的稳定性判定式。针对深部地应力场的非线性和非连续特征,采用了一种将全模拟工况测点应力作为序列而进行拟合训练的深度学习算法——长短时记忆(long short-term memory,LSTM)神经网络。以上海庙矿区鹰骏二号井田主副井空间分布区域为例,反演得到了深部煤层非连续区域地应力场分布,从而有效指导工程设计与施工。
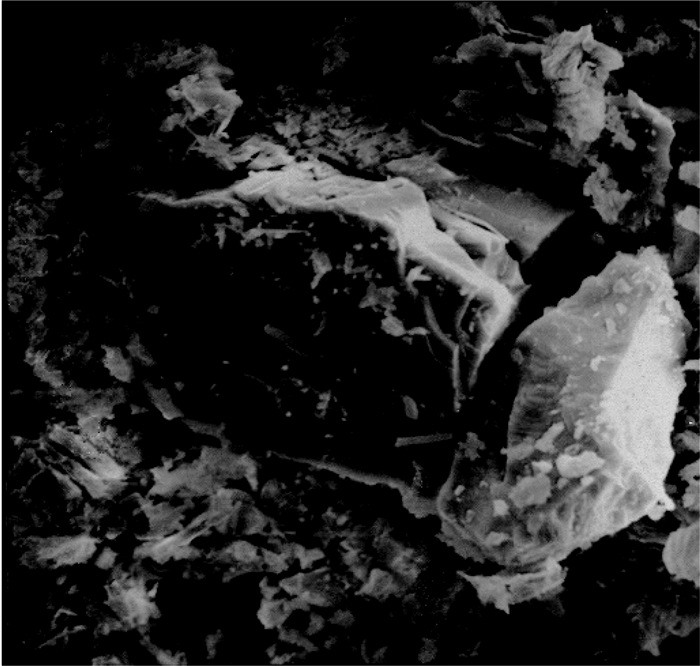
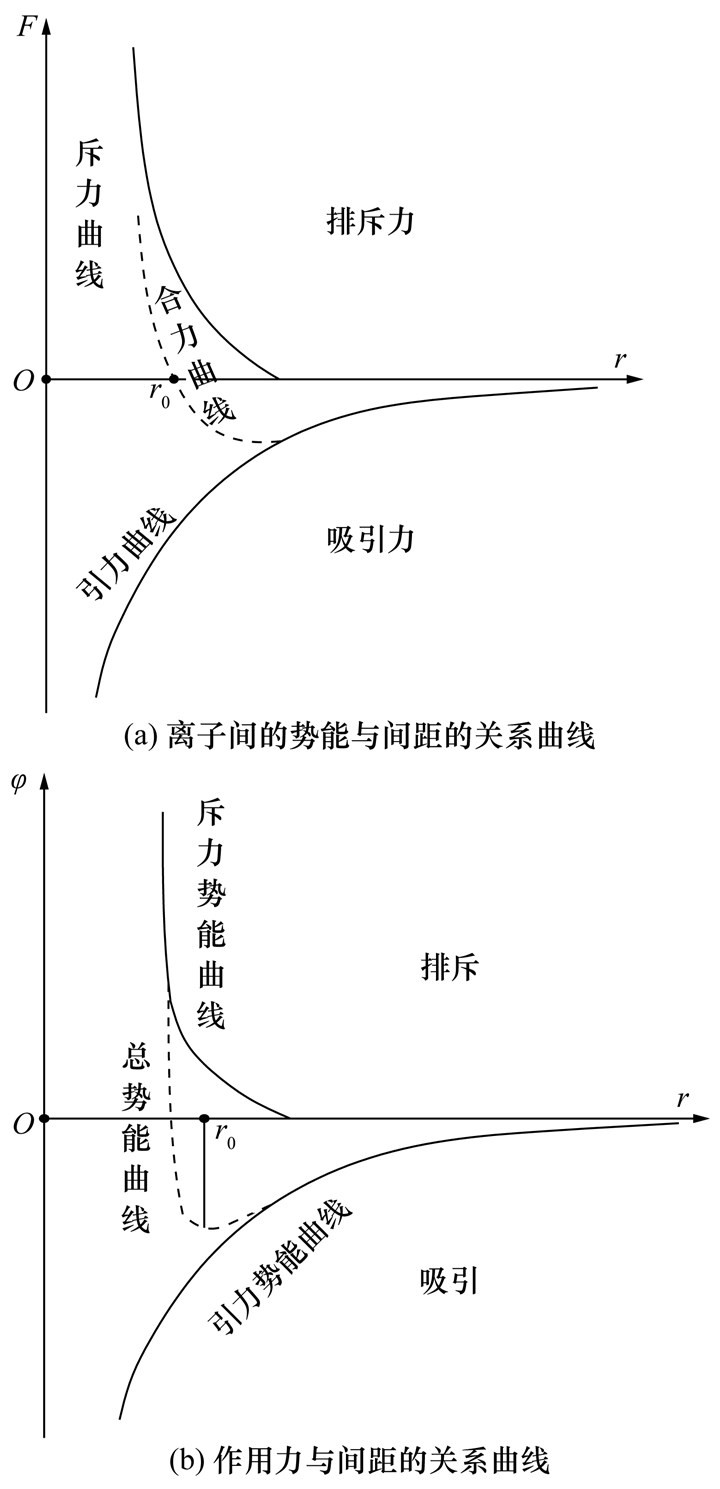
1 深部非连续区域地应力分布特征 1.1 深部地应力场宏观与微观特征地应力场的显著尺度特征可归因于岩体在微观和宏观上的表征状态及物质组成。在微观尺度上,岩体是多种矿物晶粒组成的集合体,以图 1中鹰骏二号井田深部岩石在电镜扫描下石英晶粒为例,微观应力场是由晶粒离子所构成的电磁场叠加而形成的。图 2中,未受工程扰动时,晶体内离子在电磁力作用下处于受力平衡状态,此时离子间距r = r0,总势能为0。当发生外界扰动或构造运动时,离子间距、合力变化和势能增加,之后离子会致力于回到稳定能量位置,而产生一种附加的电磁力,使离子处于受力不平衡状态。离子为达到新的平稳态往往会进行晶粒转动、晶面滑动、晶粒剪裂和破碎等方式解除部分附加电磁力,剩余未解除电磁力便形成微观地应力场[18]。
|
| 图 2 晶粒中离子势能和作用力与间距的变化关系 |
地应力场在宏观上连续充满于整个地质体,具有在时间上稳定且非独立的特征,量值和方向可视为有界和非连续的单值有势函数。岩体在外力作用下产生局部地应力场,通过应力波形式在岩体中逐步传播,局部地应力场的分布特征与岩体自身性质、岩石变形及断裂特征等因素密切相关。
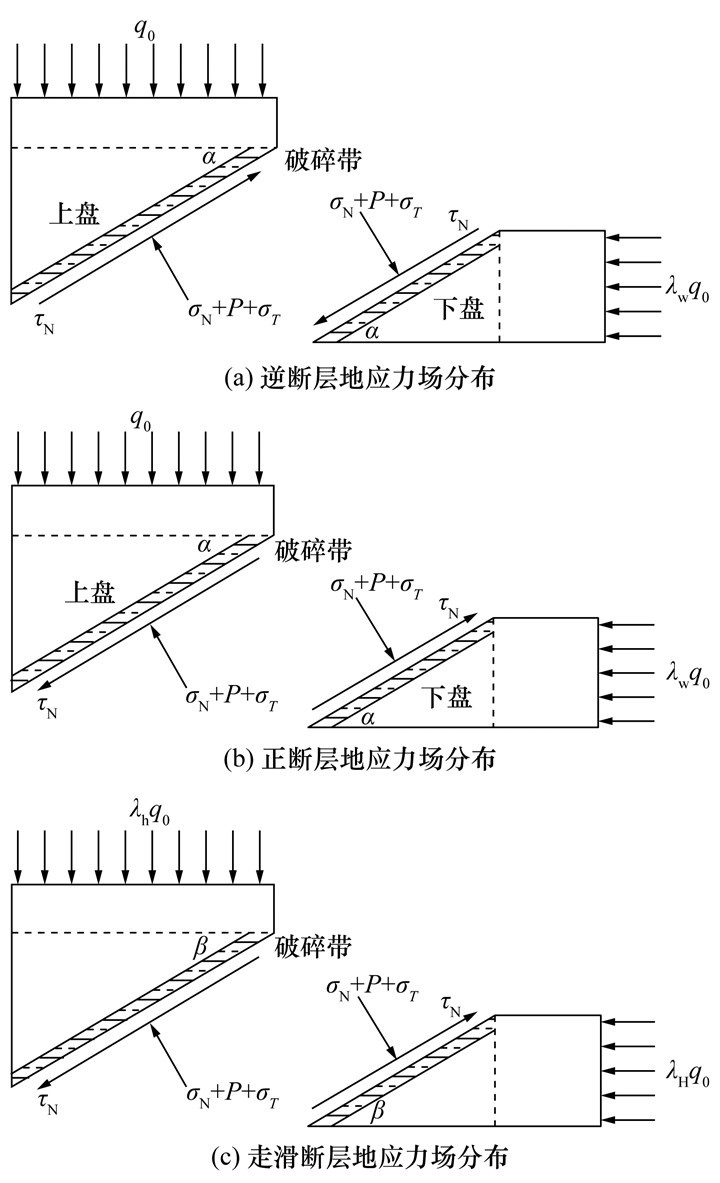
1.2 深部非连接构造区应力场界定范围根据Anderson断层理论,地应力场可分为逆断型地应力结构、正断型地应力结构及走滑型地应力结构3类[20-21]。针对3种断层滑移模式,建立图 3的地应力场分布模型。
|
| 图 3 3种断层的地应力场分布 |
图 3中,P为断层破裂带内液体及瓦斯等流体压力;σT为温度应力,由下覆含水层中温度较高岩溶水等通过裂隙涌入断层破裂带内所形成热膨胀力;σN和τN分别为断层面切向应力和法向应力;q0为上覆岩层重量;λH和λh分别为最大和最小水平主应力与垂直主应力的侧压系数;α和β分别为断层倾角和走向角;λvv为垂直于断层面处的水平应力与竖直应力之比。
根据Mohr应力圆关系,λvv可由λH和λh确定:
| $ \lambda_{\mathrm{vv}}=\frac{\left(\lambda_{\mathrm{H}}+\lambda_{\mathrm{h}}\right)}{2}-\frac{\left(\lambda_{\mathrm{H}}-\lambda_{\mathrm{h}}\right)}{2} \cos 2 \beta . $ | (1) |
根据平衡理论,并通过对图 3中的3种断层区域的地应力场分析,可获得逆断层、正断层及走滑断层切向应力和法向应力分量,分别为:
| $ \left\{\begin{array}{l} \sigma_{\mathrm{N}}=\frac{q_0\left(1+\lambda_{\mathrm{vv}}\right)-2\left(P+\sigma_T\right)}{2}-\frac{q_0\left(\lambda_{\mathrm{vv}}-1\right)}{2} \cos 2 \alpha, \\ \tau_{\mathrm{N}}=\frac{q_0\left(\lambda_{\mathrm{vv}}-1\right)}{2} \sin 2 \alpha, \end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l} \sigma_{\mathrm{N}}=\frac{q_0\left(1+\lambda_{\mathrm{vv}}\right)-2\left(P+\sigma_T\right)}{2}+\frac{q_0\left(1-\lambda_{\mathrm{vv}}\right)}{2} \cos 2 \alpha, \\ \tau_{\mathrm{N}}=\frac{q_0\left(1-\lambda_{\mathrm{vv}}\right)}{2} \sin 2 \alpha, \end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l} \sigma_{\mathrm{N}}=\left(\frac{\lambda_{\mathrm{h}} q_0-\lambda_{\mathrm{H}} q_0}{2}\right) \cos 2 \beta+\frac{\lambda_{\mathrm{H}} q_0+\lambda_{\mathrm{h}} q_0}{2}-P-\sigma_T, \\ \tau_{\mathrm{N}}=\frac{\lambda_{\mathrm{H}} q_0-\lambda_{\mathrm{h}} q_0}{2} \sin 2 \beta . \end{array}\right. $ | (4) |
结合式(2)—(4),并通过对比式(5)的直线型Mohr-Coulomb屈服准则,可得到逆断层、正断层和走滑断层区地应力场的稳定性判别式分别为式(6)、(7)和(8)。
| $ \tau_{\mathrm{N}}=c+\left(\sigma_{\mathrm{N}}-P-\sigma_T\right) \tan \varphi . $ | (5) |
其中:c为岩体黏结力,φ为岩体的内摩擦因数。
| $ \lambda_{\mathrm{H}}>-\frac{(1+\cos 2 \beta)}{(1-\cos 2 \beta)} \lambda_{\mathrm{h}}+\frac{2(1-\sin \varphi)}{(1+\sin \varphi)(1-\cos 2 \beta)}-\frac{4 c \cos \varphi-4\left(P+\sigma_T\right) \sin \varphi}{q_0(1+\sin \varphi)(1-\cos 2 \beta)}, \quad \lambda_{\mathrm{H}}>\lambda_{\mathrm{h}}>1 ; $ | (6) |
| $ \lambda_{\mathrm{H}} \leqslant-\frac{(1+\cos 2 \beta)}{(1-\cos 2 \beta)} \lambda_{\mathrm{h}}+\frac{2(1+\sin \varphi)}{(1-\sin \varphi)(1-\cos 2 \beta)}+\frac{4 c \cos \varphi-4\left(P+\sigma_T\right) \sin \varphi}{q_0(1-\sin \varphi)(1-\cos 2 \beta)}, \quad 1 \geqslant \lambda_{\mathrm{H}}>\lambda_{\mathrm{h}} ; $ | (7) |
| $ \lambda_{\mathrm{H}} \leqslant \frac{(1+\sin \varphi)}{(1-\sin \varphi)} \lambda_{\mathrm{h}}+\frac{2 c \cos \varphi-2 \sin \varphi\left(P+\sigma_T\right)}{q_0(1-\sin \varphi)}, \quad \lambda_{\mathrm{H}}>1>\lambda_{\mathrm{h}} . $ | (8) |
地应力场反演计算归属于Hilbert空间上寻找最佳逼近元的问题[9, 22],具体求解步骤为:首先,在有限元计算模型各边界施加不同的应力(位移)载荷条件去产生由应力数据组成的子空间,并对研究区域的不同类型的断层地应力分布范围进行界定,筛选出合理的计算工况;然后,分别将计算工况的地应力数据与实测地应力数据整理,组成Hilbert空间上的子集空间,若由实测数据组成的子集空间维度小于计算应力子空间维度,采用多元线性回归、遗传算法等方法即可获得较高的反演精度。但深部地层受特殊地质环境、多变的岩体属性和显著的多场耦合效应等因素影响,实测地应力数据具有高维度、非线性等特征,组成的子空间维度往往高于计算应力子空间维度,无疑给寻优带来了巨大困难。因此,建立基于LSTM神经网络算法的深部地应力场反演方法可实现样本子空间降维和各基底子空间(计算应力子空间)深度优化,从而明显反演精度。
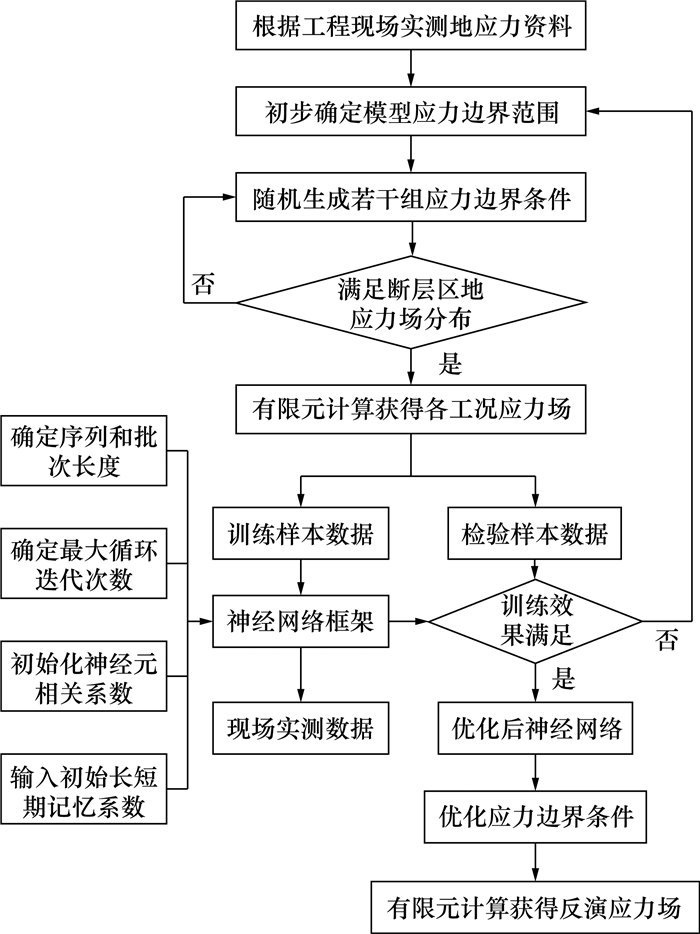
图 4中,该反演方法总体流程包括有限元计算模型构建、非连续构造区应力场界定、地应力数据获取、神经网络算法模型训练、模型测试及模型应用。
|
| 图 4 基于LSTM神经网络的反演方法 |
2.2 LSTM神经网络算法
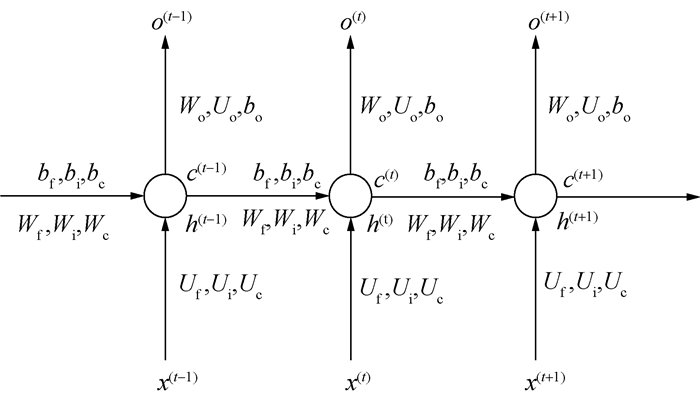
LSTM神经网络是将各计算工况的测点应力资料及现场实测数据分别作为训练样本及预测样本,并将训练样本视为不同序列,以循环学习方式更新权值与偏置值等,基本结构如图 5所示。该算法具有坚实理论基础,对序列“记忆”问题有广泛适用性,可解决传统网络算法长期记忆能力不足、梯度消失及爆炸等问题[23-24]。在高维度、非线性的深部应力场反演中,该算法的计算误差值可逐渐趋于零,具有稳定收敛与预测精度高等优点。
|
| 图 5 LSTM神经网络结构及信息序列学习 |
图 5中,x(·)、c(·)、h(·)和o(·)分别为不同时刻输入值、长期记忆状态、短期记忆状态和输出值。Wf和Uf为遗忘门的权值,bf为遗忘门的偏置值。Wi、Wc、Ui、Uc为输入门的权值,bi和bc为输入门的偏置值。Wo和Uo为输出门的权值,bo为输出门偏置值。
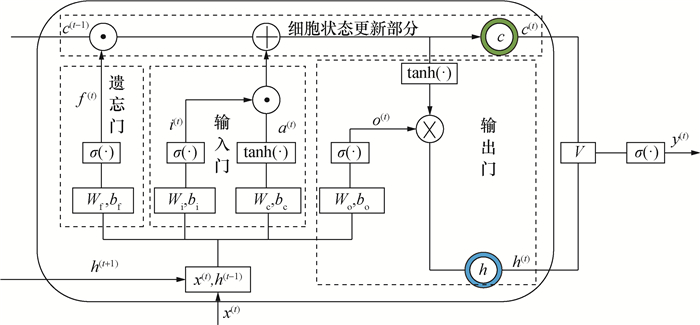
神经网络算法模型中的遗忘门、输入门、细胞状态更新部分和输出门4个学习体的拓扑结构如图 6所示。
|
| 图 6 学习体的拓扑结构 |
图 6中,Sigmoid和tanh激活函数分别为式(9)和(10)。各部分学习体作用见表 1,其中⊙为向量对应元素相乘符号。
| $ \sigma(z) =\frac{1}{1+\mathrm{e}^{-z}} , $ | (9) |
| $ \operatorname{tanh}(z) =\frac{\mathrm{e}^z-\mathrm{e}^{-z}}{\mathrm{e}^z+\mathrm{e}^{-z}}. $ | (10) |
| 学习体 | 计算公式 | 主要功能 |
| 遗忘门 | f(t)=σ(Wfh(t-1)+Ufx(t)+bf) | 输入量包括先前地层应力记忆状态h(t-1)和当前测点地应力数据x(t),通过式(9)的sigmoid激活函数,获得遗忘门输出量f(t),达到剔除误差较大的应力数据,提高整体地应力场的反演精度 |
| 输入门 | i(t)=σ(Wih(t-1)+Uix(t)+bi) a(t)=tanh(Wch(t-1)+Ucx(t)+bc) |
输出量为i(t)和tanh激活函数(见式(10))的输出量a(t),可综合分析处理当前地应力信息与先前地应力记忆信息,从而完成地应力信息充分挖掘 |
| 细胞状态更新部分 | c(t)=c(t-1)⊙f(t)+i(t)⊙a(t) | 该部分的作用是更新并保持长期优良地应力数据记忆状态,即结合当前及先前应力数据资料进行深度学习,并以一定的概率控制是否遗忘先前训练样本信息c(t-1),从而优化地应力资料记忆信息c(t) |
| 输出门 | o(t)=σ(Woh(t-1)+Uox(t)+bo) h(t)=o(t)⊙tanh(c(t)) |
该部分的作用是综合地应力的学习资料o(t)及先前地应力记忆信息资料c(t),更新整体记忆信息h(t) |
通过对表 1中的各学习体依次计算,可得到短期记忆信息h(t),从而可得到算法拟合值y(t):
| $ y^{(t)}=\sigma\left(V h^{(t)}+c\right) . $ | (11) |
其中:V和c分别为输出层神经元权值和阈值。
采用误差反向传播算法[25]对模型中的各参数训练与优化,形成式(12)的算法拟合值与实际值误差平方和最小化形式的目标函数。
| $ E_{\mathrm{d}}=\frac{1}{2} \sum\limits_{i=1}^N\left(y_i-\hat{y}_i\right)^2 . $ | (12) |
其中:Ed的误差平方值,yi和
基于各模拟工况的应力测点数值序列,各参数的优化采用式(13)的误差反向传播的随机梯度下降算法[25]。
| $ \theta_j^{n+1}=\theta_j^n-\alpha \frac{\partial E_{\mathrm{d}}}{\partial \theta_j^n} . $ | (13) |
其中:α为更新系数;θjn+1和θjn分别为第(n+1)次和第n次迭代步中待优化参数,包括Wf、Uf、bf、Wi、Wc、Ui、Uc、bi、bc、Wo、Uo、bo、c(t)、h(t)。
3 鹰骏二号井田地应力计算模型 3.1 工程概况及构造历史鹰骏二号井田位于华北板块西部的鄂尔多斯盆地边缘,地形北高南低,东高西低,呈缓波状起伏,海拔高度范围为1 316~1 379 m。井田全部被新生界中的第四系全新统、中更新统和上更新统地层及第三系地层所覆盖,岩层以砂岩、沉积碎屑岩、粉砂岩、泥岩等为主。含水层以裂隙充水为主,总体为弱至中等富水性,地下水补给条件差,水文地质边界较复杂。含煤地层为侏罗系延安组,平均厚度为263.91 m,可采煤层有9层(八煤和十五煤等)。煤层总体缓倾斜,走向近南北方向,倾角为5°~30°,顶底板多为中硬细粒砂岩和软弱的粉砂岩等。新上海庙背斜、清水营向斜及背斜等构造轴向均为近南北方向,井田断层较发育,共有38条断层,以东北或北北东走向的逆断层为主。
区域构造应力场复杂多变,在印支期受由南向北推挤作用,在印支亚旋回的早期,区域升降运动使得缺失早三叠世沉积,但原有构造格局没有显著改变,沉积了三叠系中、上统。在印支亚旋回晚期,由于区域出现大规模上升运动,造成了延长组瓦窑堡组及早侏罗世富县组在矿区内剥蚀殆尽,延安组与下伏延长组间假整合接触。在燕山期,受北西—南东向应力场作用,由南东向北西推挤而产生了一系列北西向构造。在燕山亚旋回早期,升降运动沉积了侏罗系中统延安组、直罗组和安定组。燕山亚旋回的中期,构造运动剧烈,形成一系列近南北走向的褶曲及断裂,并以角度不整合沉积于前期地层之上。在燕山亚旋回的晚期,地层在前期构造格局的基础上,再度褶皱隆起,之后区域构造趋于稳定。在喜山运动时期,受南西向北东推挤作用,造成区内一些具右行张扭性质的近南北向断裂构造及呈右行排列的低角度宽缓褶皱。在喜山旋回时期,升降运动强烈,沉积厚度达3 000 m。第四纪、古近纪时,构造运动相对较弱,地层仅有小型褶曲及断裂。
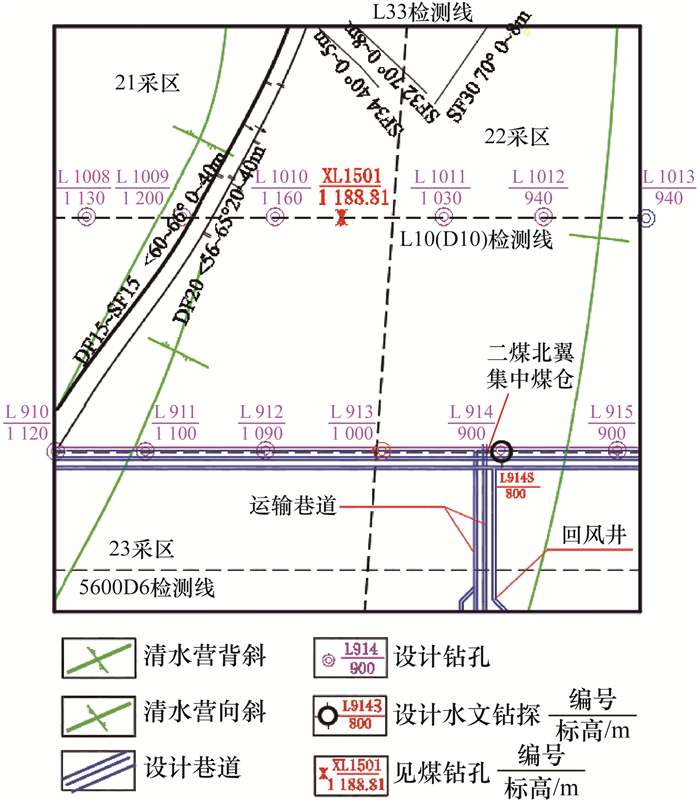
3.2 建模区域确定及模型建立为减少矿井保护煤柱压煤量和优化矿井运输系统及深部开采工作效率,将主、副、风井及工业广场布置在井田中部清水营背斜核部的上方,选取的建模区域如图 7所示。
|
| 图 7 建模区域 |
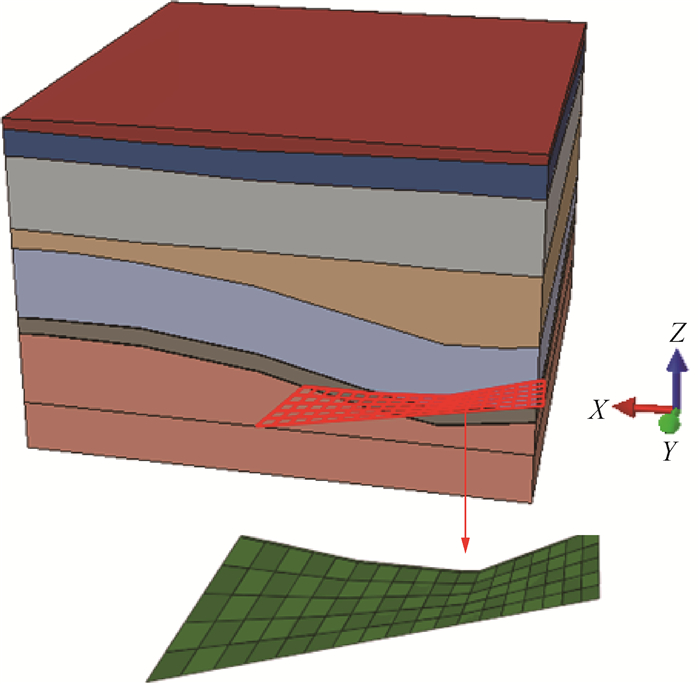
将地层及断层坐标整理,采用Civil3D软件建模并导入ABAQUS软件中,形成图 8的地质模型。地质体划分9层,包括7个岩层及2个深部可采煤层(八煤和十五煤)。模型中红色面为DF15与SF15大型正断层带,该断层带位于井田中部,向南北两端逐渐延伸尖灭,错断清水营背斜核部残余煤系地层。走向方位为北东向,倾向北西向,倾角约22°,落差0~20 m,延展长度约540 m。另外,小型断层SF34、SF32和SF30在模型中已概化,但需按式(6)—(8)对区域应力场进行合理性判定。
|
| 图 8 三维地质模型 |
在地质模型中,X轴范围为4 000~6 000 m,表征为东西向,西起清水营向斜、东至清水营背斜东。Y轴为南北向,范围为0~2 000 m,南起5600D6勘探线,北至D10勘探线以北500 m。Z轴为竖直向,由地表(约1 360 m水平)到0 m水平,深度约为1 360 m。
由于井田地层岩性复杂且变异性大,概化后的地层力学参数参考来自现场的不同深度和岩性的岩石室内试验结果,参考文[5],确定出煤层及岩土体物理力学参数如表 2所示。大型断层破碎带采用嵌入cohesive单元层方式模拟,结构面法向及切向刚度为5 GPa,破裂带填充物密度为1 600 kg·m-3。
| 地层 | 密度/(kg·m-3) | 弹性模量/GPa | Poisson比 | 黏聚力/MPa | 内摩擦角/(°) | 抗拉强度/MPa |
| 第一层 | 2 200 | 3.060 | 0.212 | 1.350 | 36.000 | 0.840 |
| 第二层 | 2 250 | 5.670 | 0.460 | 1.920 | 42.610 | 1.280 |
| 第三层 | 2 310 | 7.220 | 0.235 | 2.170 | 40.020 | 0.840 |
| 第四层 | 2 310 | 7.220 | 0.235 | 2.190 | 38.130 | 0.840 |
| 第五层 | 2 360 | 9.905 | 0.232 | 2.170 | 40.020 | 1.385 |
| 八煤 | 1 540 | 5.000 | 0.400 | 1.400 | 30.000 | 0.800 |
| 第七层 | 2 230 | 5.600 | 0.184 | 1.920 | 42.610 | 1.430 |
| 十五煤 | 1 540 | 5.000 | 0.400 | 1.400 | 30.000 | 0.800 |
| 第九层 | 2 270 | 5.570 | 0.214 | 1.940 | 48.190 | 1.270 |
3.3 区域地应力场测量结果
由于深部地层具有显著的非连续性,且岩性变化较大,为保证测点位于主要工业设施场地和首采区,选取L911及L1012勘探孔开展水压致裂法测量地应力。测量时保证各测段岩性不同,尽可能避开含水层、煤层顶底板及断层破裂带。两测段破裂形态为直立裂缝,方向为N223.0°E、N269.0°E。舍去测量中操作误差较大测段后,结果如表 3和4所示。其中,SH、Sh和Sv分别为最大水平主应力、最小水平主应力和竖直应力。
| 测点编号 | 测段深度/ m | 主应力值/MPa | ||
| SH | Sh | Sv | ||
| L911-1 | 256.54 | 8.64 | 4.56 | 5.64 |
| L911-2 | 351.63 | 12.12 | 6.51 | 7.74 |
| L911-3 | 445.56 | 15.62 | 9.63 | 9.80 |
| L911-4 | 513.15 | 17.50 | 10.77 | 11.29 |
| L911-5 | 634.53 | 21.81 | 13.23 | 13.96 |
| L911-6 | 702.65 | 23.65 | 13.82 | 15.46 |
| L911-7 | 756.24 | 25.94 | 16.13 | 16.64 |
| 测点编号 | 测段深度/ m | 主应力值/MPa | ||
| SH | Sh | Sv | ||
| L1012-1 | 189.73 | 6.79 | 3.28 | 4.17 |
| L1012-2 | 284.55 | 9.09 | 5.01 | 6.26 |
| L1012-3 | 365.85 | 12.22 | 6.19 | 8.05 |
| L1012-4 | 501.35 | 16.35 | 8.87 | 11.03 |
| L1012-5 | 609.75 | 19.70 | 11.16 | 13.41 |
| L1012-6 | 704.65 | 22.68 | 13.83 | 15.50 |
4 地应力反演分析 4.1 地应力场反演计算流程
1) 约束模型下表面的竖向位移,上地表设置为无约束的自由面,并分别在垂直于X轴且与X=4 000为交点的模型竖向表面(简称“X=4 000面”)和Y轴且与Y=0为交点的模型竖向表面(简称“Y=0面”)施加法向约束,在垂直于X轴且与X=6 000为交点的模型竖向表面(简称“X=6 000面”)和Y轴且与Y=2 000为交点的模型竖向表面(简称“Y=2 000面”)施加10组不同量值的均匀压应力及线性增加的压应力边界条件,并在模型整体施加10组不同重力加速度,从而获得10组计算工况条件下的地应力场。
2) 对未进行断层建模的中小型SF34、SF32和SF30断层的地质条件进行解译,根据式(6)—(8)对各断层区域的应力场范围进行合理界定。即取各计算工况的对应断层位置的应力值,与式(6)—(8) 对比验证是否满足应力场稳定性条件,筛选出不满足的计算工况,进行模型边界条件重新选取并计算,直到10组计算工况均满足断层应力的界定范围。
3) 将10组工况测点应力值作为训练样本输入量,边界条件、重力加速度作为训练样本输出量,代入LSTM算法中训练,隐含层节点个数设置为20,序列长度设置为5,控制系数更新的批次长度设置为20,循环训练次数设置为30。
4) 将工程现场测点应力数据代入优化后的LSTM算法中,输出量是能够反映实际应力场的边界条件,如式(14)所示,而重力加速度为9.732 m/s2。将式(14)的最优化边界条件代入的LSTM算法模型中,可计算出区域地应力场。
| $ \left\{\begin{array}{l} p_x(h)=1.756 \times 10^4 h+5.149 \times 10^6, \\ p_{x y}(h)=-3.509 \times 10^2 h+2.749 \times 10^4, \\ p_y(h)=1.311 \times 10^4 h+2.101 \times 10^6, \\ p_{y x}(h)=-2.402 \times 10^2 h-4.887 \times 10^5 . \end{array}\right. $ | (14) |
其中:h为岩体埋深,单位为m;px(h)和py(h)分别为X=4 000面和Y=0面的挤压载荷条件,以挤压地应力为正;pxy(h)和pyz(h)分别为X=4 000面和Y=0面的水平剪切载荷条件,分别以Y和X轴的指向为正,单位为Pa。
4.2 地应力场反演结果分析1) 测点地应力的实测值和反演值比较。
表 5和6分别为L911钻孔和L1012钻孔测点地应力分量反演值,与表 3和4对应的实测值比较可知,测点地应力反演值与实测值吻合度高,平均误差为12.897%,相关系数为0.945,误差值的标准差为2.000,反演精度较高,结果可靠。
| 测点编号 | 测段深度/ m | 主应力值/MPa | ||
| SH | Sh | Sv | ||
| L911-1 | 256.54 | 11.72 | 4.31 | 5.03 |
| L911-2 | 351.63 | 12.85 | 6.66 | 6.86 |
| L911-3 | 445.56 | 14.00 | 8.91 | 8.49 |
| L911-4 | 513.15 | 14.27 | 10.09 | 10.13 |
| L911-5 | 634.53 | 15.54 | 12.16 | 12.30 |
| L911-6 | 702.65 | 20.19 | 15.93 | 14.07 |
| L911-7 | 756.24 | 20.76 | 16.74 | 15.21 |
| 测点编号 | 测段深度/ m | 主应力值/MPa | ||
| SH | Sh | Sv | ||
| L1012-1 | 256.54 | 9.25 | 4.92 | 4.08 |
| L1012-2 | 351.63 | 10.83 | 5.89 | 6.23 |
| L1012-3 | 445.56 | 11.88 | 6.92 | 8.62 |
| L1012-4 | 513.15 | 13.17 | 7.83 | 11.19 |
| L1012-5 | 634.53 | 18.14 | 10.77 | 15.27 |
| L1012-6 | 702.65 | 20.28 | 11.93 | 17.93 |
2) 区域地应力场分布规律。
基于区域地应力场反演结果,研究井田开采区的初始地应力场分布,以期为主副井合理支护以及巷道合理规划等工程提供依据。
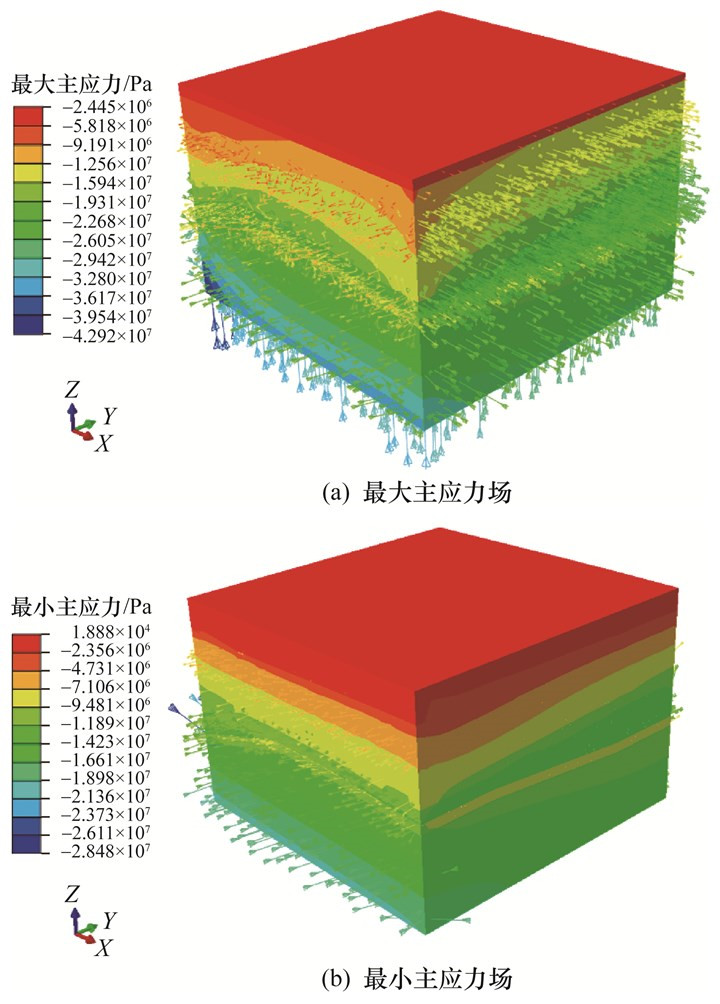
图 9中,最大主地应力场在浅部以水平为主,分带不明显,深部以竖向为主,分层明显,范围为1.63~40.52 MPa。DF15大型断层区域的最大主地应力范围为2.68~27.22 MPa,与围岩相比,断层带内地应力降低、断层尖灭端地应力集中,且地应力方向沿着断层走向偏转。另外,最小主地应力场以水平为主,最大值为26.90 MPa,地表因高程差异出现少许拉应力区,竖向分层现象明显、水平分带不明显。区域地应力场具有显著的煤矿沉积特征,白垩系、侏罗系、三叠系地层的主副竖井应重视NWW~SSW弧度的稳定性,及时卸压支护,且巷道轴线方向应布置在南南西至北西西方向(223°~269°)。
|
| 图 9 矿区主应力场分布矢量图 |
3) 主采煤层及顶底板地应力场分布规律。
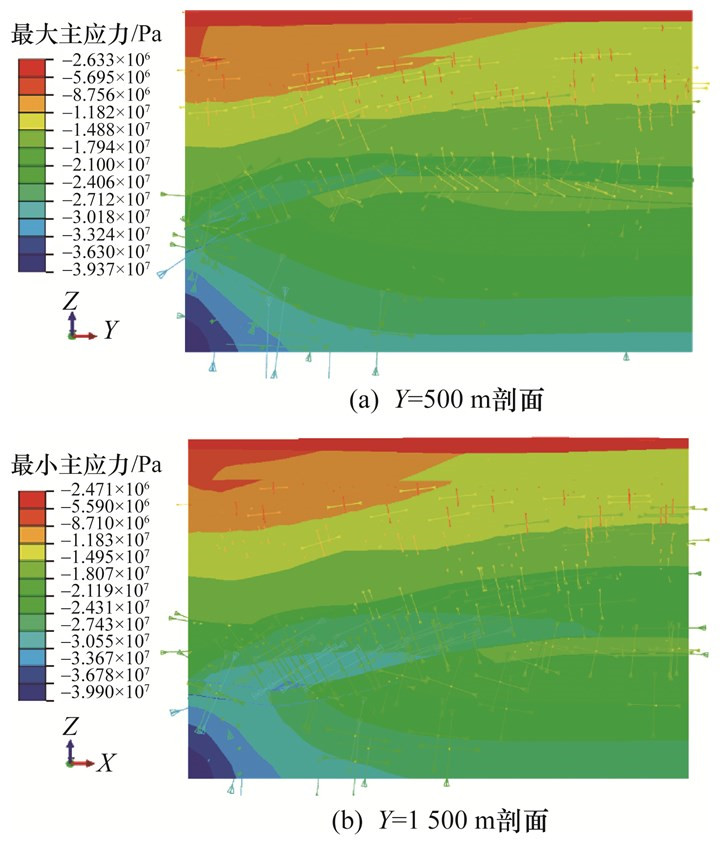
沿模型东西向选取典型剖面Y=500 m和Y=1 500 m,分别得到图 10和11最大地应力场矢量图。
|
| 图 10 模型东西向典型剖面主应力矢量图 |
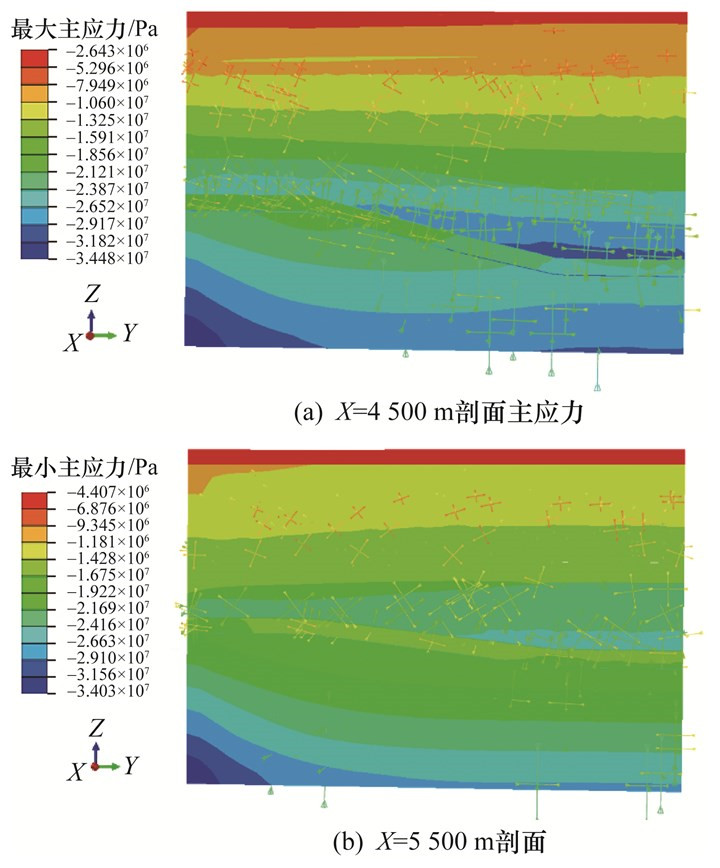
|
| 图 11 模型南北向典型剖面主应力矢量图 |
图 10中,八煤顶板多数区域应力值变化较小,主应力范围为19.7~26.19 MPa,方向大致平行于煤层倾向。位于清水营背斜核部的煤层顶板应力集中,最大值达到35.32 MPa,这与燕山亚旋回期地层上升并受到来自东西方向上的挤压力作用密切相关。底板岩体应力值小于顶板岩石应力值,这由于八煤底板岩体以砂岩等软岩为主而不利于应力积累。鉴于软岩渗透性相对较大且下覆岩层存在含水层,可初步断定煤层底板及巷道易出现涌水现象,采场及巷道的底板需加强防水处理。在八煤开采过程中,注意背斜核部顶板岩层应力集中带来冲击倾向性问题,及时采取爆破或大钻孔卸压等措施。十五煤的顶板岩层为八煤的底板岩层,防水也是该煤层开采及巷道安全性的重点,底板岩石应力量值变化小,最大主应力方向近似垂直于煤层倾向。
图 11分别为模型南北向典型剖面X=4 500 m和X=5 500 m的区域地应力场分布。由图 11可知,地应力集中区域为八煤顶板岩层,底板岩层地应力较小,八煤和顶底板区域的最大主应力在水平与竖直2个方向均存在,表明矿区的在先前经历过较强的构造运动作用,岩体各向异性明显。十五煤层区域应力变化相对较小,这表明该煤层沉积阶段,构造运动相对较弱,沉积作用相对明显。
5 结论本文根据深部煤层地应力场显著的非连续和非线性特征,界定了深部逆断层、正断层及走滑断层区域地应力场分布范围,建立了基于LTMS神经网络算法的反演方法,并以上海庙矿区鹰骏二号井田主副井区域为例采用了该方法。主要结论如下:
1) 上海庙矿区鹰骏二号地应力反演精度较高,因此,考虑断层构造区域地应力场的分布规律对于提高深部应力场的反演精度至关重要,有效验证了该方法的有效性。
2) 深部十五煤层顶板及底板地应力较小,无应力集中区,上覆八层煤在沉积过程中受到水平方向上的挤压力作用产生倾斜产状,倾斜区顶板存在应力集中。DF15大型断层带的地应力场与区域地应力场相比,量值降低约5 MPa,并发生逆时针方向偏转。因此,对于井田深部煤层开采,可采用保护层开采方式,即先行开采下部的十五煤,为八煤的开采提供保护卸压作用,从而保证井田深部开采的安全性与可靠性。
3) 地质构造是影响矿山深部地应力场分布的主控因素。不同类型断层的区域应力场的量值和方向均会发生变化,正断层区地应力场出现显著的地应力衰减现象,逆断层区域地应力场增幅显著,走滑断层区域的岩体剪切地应力值有所增加。褶皱构造主要控制水平地应力场分布;与同深度水平条件下的连续性沉降地层地应力场相比,背斜及内弧轴部区段地应力相对较大,而向斜外弧区段地应力相对较小。
| [1] |
谢和平. 深部岩体力学与开采理论研究进展[J]. 煤炭学报, 2019, 44(5): 1283-1305. XIE H P. Research review of the state key research development program of China: Deep rock mechanics and mining theory[J]. Journal of China Coal Society, 2019, 44(5): 1283-1305. (in Chinese) |
| [2] |
谢和平, 李存宝, 高明忠, 等. 深部原位岩石力学构想与初步探索[J]. 岩石力学与工程学报, 2021, 40(2): 217-232. XIE H P, LI C B, GAO M Z, et al. Conceptualization and preliminary research on deep in situ rock mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(2): 217-232. (in Chinese) |
| [3] |
周家兴. 基于深度学习的深部复杂地应力场反演算法研究[D]. 北京: 北京科技大学, 2022. ZHOU J X. Research on inversion algorithm of deep complex in-situ stress field based on depth learning[D]. Beijing: University of Science and Technology Beijing, 2022. (in Chinese) |
| [4] |
薛成春, 曹安业, 牛风卫, 等. 深部不规则孤岛煤柱区冲击地压机理及防治[J]. 采矿与安全工程学报, 2021, 38(3): 479-486. XUE C C, CAO A Y, NIU F W, et al. Mechanism and prevention of rock burst in deep irregular isolated coal pillar[J]. Journal of Mining & Safety Engineering, 2021, 38(3): 479-486. (in Chinese) |
| [5] |
李飞, 周家兴, 王金安. 深部多场耦合作用的非线性地应力构建方法[J]. 煤炭学报, 2021, 46(S1): 116-129. LI F, ZHOU J X, WANG J A. Method of nonlinear in-situ stress construction with deep multi-field coupling[J]. Journal of China Coal Society, 2021, 46(S1): 116-129. (in Chinese) |
| [6] |
贺虎. 煤矿覆岩空间结构演化与诱冲机制研究[J]. 煤炭学报, 2012, 37(7): 1245-1246. HE H. Research on the evolution mechanism of spatial structure of overlying strata and rockburst inducing in coal mine[J]. Journal of China Coal Society, 2012, 37(7): 1245-1246. (in Chinese) |
| [7] |
韩科明, 于秋鸽, 张华兴, 等. 上下盘开采影响下断层滑移失稳力学机制[J]. 煤炭学报, 2020, 45(4): 1327-1335. HAN K M, YU Q G, ZHANG H X, et al. Mechanism of fault activation when mining on hanging-wall and foot-wall[J]. Journal of China Coal Society, 2020, 45(4): 1327-1335. (in Chinese) |
| [8] |
高明忠, 王明耀, 谢晶, 等. 深部煤岩原位扰动力学行为研究[J]. 煤炭学报, 2020, 45(8): 2691-2703. GAO M Z, WANG M Y, XIE J, et al. In-situ disturbed mechanical behavior of deep coal rock[J]. Journal of China Coal Society, 2020, 45(8): 2691-2703. (in Chinese) |
| [9] |
周家兴, 王金安, 李飞. 深部工程岩体温度与渗流耦合作用下复杂应力场反演方法[J/OL]. 工程力学. DOI: 10.6052/j.issn.1000-4750.2022.05.0495. ZHOU J X, WANG J A, LI F. Inversion method for complex stress field under coupling effect of temperature and seepage in deep engineering rock mass[J/OL]. Engineering Mechanics. DOI: 10.6052/j.issn.1000-4750.2022.05.0495.(inChinese) |
| [10] |
李飞, 周家兴, 王金安. 基于稀少样本数据的地应力场反演重构方法[J]. 煤炭学报, 2019, 44(5): 1421-1431. LI F, ZHOU J X, WANG J A. Back-analysis and reconstruction method of in-situ stress field based on limited sample data[J]. Journal of China Coal Society, 2019, 44(5): 1421-1431. (in Chinese) |
| [11] |
王金安, 李飞. 复杂地应力场反演优化算法及研究新进展[J]. 中国矿业大学学报, 2015, 44(2): 189-205. WANG J A, LI F. Review of inverse optimal algorithm of in-situ stress filed and new achievement[J]. Journal of China University of Mining & Technology, 2015, 44(2): 189-205. (in Chinese) |
| [12] |
刘泉声, 王栋, 朱元广, 等. 支持向量回归算法在地应力场反演中的应用[J]. 岩土力学, 2020, 41(S1): 319-328. LIU Q S, WANG D, ZHU Y G, et al. Application of support vector regression algorithm in inversion of geostress field[J]. Rock and Soil Mechanics, 2020, 41(S1): 319-328. (in Chinese) |
| [13] |
陈世杰, 肖明, 陈俊涛, 等. 断层对地应力场方向的扰动规律及反演分析方法[J]. 岩石力学与工程学报, 2020, 39(7): 1434-1444. CHEN S J, XIAO M, CHEN J T, et al. Disturbance law of faults to in-situ stress field directions and its inversion analysis method[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(7): 1434-1444. (in Chinese) |
| [14] |
裴启涛, 丁秀丽, 卢波, 等. 考虑地应力分布形式的坝址区初始应力场二次反演方法[J]. 岩土力学, 2016, 37(10): 2961-2970. PEI Q T, DING X L, LU B, et al. Two-stage back analysis method of initial geostress field in dam areas considering distribution characteristics of geostress[J]. Rock and Soil Mechanics, 2016, 37(10): 2961-2970. (in Chinese) |
| [15] |
陈爽, 白根铭, 肖畅, 等. 断层构造对高地应力隧道初始地应力场影响分析[J]. 中国安全科学学报, 2023, 33(2): 146-151. CHEN S, BAI G M, XIAO C, et al. Analysis of influence of fault structure on initial ground stress field of high ground stress tunnel[J]. China Safety Science Journal, 2023, 33(2): 146-151. (in Chinese) |
| [16] |
寇昊, 何川, 吴枋胤, 等. 考虑走滑断裂活动影响的公路隧道初始地应力场反演分析[J]. 中国公路学报, 2022, 35(9): 321-330. KOU H, HE C, WU F Y, et al. Inversion analysis of initial geostress field of highway tunnel considering influence of strike-slip fault activity[J]. China Journal of Highway and Transport, 2022, 35(9): 321-330. (in Chinese) |
| [17] |
吕进国, 姜耀东, 李守国, 等. 巨厚坚硬顶板条件下断层诱冲特征及机制[J]. 煤炭学报, 2014, 39(10): 1961-1969. LÜ J G, JIANG Y D, LI S G, et al. Characteristics and mechanism research of coal bumps induced by faults based on extra thick and hard roof[J]. Journal of China Coal Society, 2014, 39(10): 1961-1969. (in Chinese) |
| [18] |
安欧. 构造应力场[M]. 2版. 北京: 地震出版社, 2021. AN O. Structural stress field[M]. 2nd ed. Beijing: Seismological Press, 2021. (in Chinese) |
| [19] |
周勇. 弱胶结极松软地层井巷工程围岩稳定性及控制技术研究[D]. 北京: 北京科技大学, 2022. ZHOU Y. Study on stability and control technology of tunnel surrounding rock in weak cementation and extremely soft stratum[D]. Beijing: University of Science and Technology Beijing, 2022. (in Chinese) |
| [20] |
李鹏, 郭奇峰, 苗胜军, 等. 浅部和深部工程区地应力场及断裂稳定性比较[J]. 哈尔滨工业大学学报, 2017, 49(9): 10-16. LI P, GUO Q F, MIAO S J, et al. Comparisons of in-situ stress fields and stability of faults in shallow and deep engineering areas[J]. Journal of Harbin Institute of Technology, 2017, 49(9): 10-16. (in Chinese) |
| [21] |
林远东, 涂敏, 付宝杰, 等. 断层自锁与活化的力学机理及稳定性控制[J]. 采矿与安全工程学报, 2019, 36(5): 898-905. LIN Y D, TU M, FU B J, et al. Mechanical mechanisms of fault self-locking and activation and its stability control[J]. Journal of Mining & Safety Engineering, 2019, 36(5): 898-905. (in Chinese) |
| [22] |
刘培德. 泛函分析基础[M]. 北京: 科学出版社, 2006. LIU P D. Fundamentals of generalized functional analysis[M]. Beijing: Science Press, 2006. (in Chinese) |
| [23] |
CAI T, DENG Z W, PARK Y, et al. Acquisition of kHz-frequency two-dimensional surface temperature field using phosphor thermometry and proper orthogonal decomposition assisted long short-term memory neural networks[J]. International Journal of Heat and Mass Transfer, 2021, 165: 120662. |
| [24] |
尹学振, 赵慧, 赵俊保, 等. 多神经网络协作的军事领域命名实体识别[J]. 清华大学学报(自然科学版), 2020, 60(8): 648-655. YIN X Z, ZHAO H, ZHAO J B, et al. Multi-neural network collaboration for Chinese military named entity recognition[J]. Journal of Tsinghua University (Science and Technology), 2020, 60(8): 648-655. DOI:10.16511/j.cnki.qhdxxb.2020.25.004 (in Chinese) |
| [25] |
邓建华. 深度学习: 原理、模型与实践[M]. 北京: 人民邮电出版社, 2021. DENG J H. Deep learning: Principles, models and practice[M]. Beijing: Posts & Telecom Press, 2021. (in Chinese) |