2. 西安科技大学 计算机科学与技术学院,西安 710054
2. College of Computer Science and Technology, Xi'an University of Science and Technology, Xi'an 710054, China
注塑成型是将黏弹性聚合物熔体注入模具后固化成型的一类加工方法。塑料制品的强度、韧性等性能受熔体内部微观分子结构的影响,因此研究注塑成型过程中的微观分子结构演化对于优化制品性能、提高生产效率具有重要意义。由于注塑成型实验操作成本高、设计周期长,且聚合物熔体内部存在复杂的流变特性和微观分子结构演化,数值模拟已成为研究黏弹性注塑成型的重要手段。
对于注塑成型的数值模拟,传统的有限元法(finite element method, FEM)、有限体积法(finite volume method, FVM)和有限差分法(finite difference method, FDM) 等网格类数值方法已经得到了应用[1-3]。然而,注塑成型过程涉及复杂的前沿界面,因此该问题的数值模拟还需要施加额外的界面追踪技术[4-5],致使其程序编制复杂、实施过程繁琐。近40年来,一种基于Lagrange描述的无网格粒子类方法,光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法,由于免去了生成网格的繁琐操作,避免了传统网格的缠结和扭曲且方便追踪熔体前沿界面,逐渐成为计算流体力学领域的新兴数值方法[6]。Lucy等[7-8]于1977年首次提出了SPH方法,并应用于天体物理学问题。Monaghan[9]给出了Navier-Stokes方程的对称化SPH离散公式,并推广到溃坝流等自由表面流动问题的数值模拟中。Ellero等[10]基于SPH方法数值模拟了低Reynolds数下的黏弹性Poiseuille流,其中流体的黏弹特性通过Oldroyd-B模型和上随体Maxwell模型进行建模和计算。关于SPH方法的更详细介绍,可参阅Liu等[11]的综述论文。
注塑成型过程本质上是黏弹性流体的流动过程,已有不少学者开展了黏弹性流体的SPH数值模拟研究。除了上述Ellero等[10]的研究工作外,Ghysels等[12]通过SPH方法将植物细胞建模为黏弹性流体,模拟了细胞变形问题。Hashemi等[13]采用弱可压缩SPH方法模拟了含有圆柱体和豆状截面柱体的黏弹性流体流动问题。Vázquez-Quesada等[14]基于SPH方法模拟了黏弹性流体在通道内绕圆柱流动问题,并分析了Weissenberg数的影响。Bao等[15]提出了一种具有可变光滑长度的SPH方法,实现了虚拟手术训练系统中的黏弹性血液流动的数值模拟。Heck等[16]提出了具有扩展边界条件的SPH方法,模拟了黏弹性细胞相互作用过程。Dos Santos Brito等[17]使用SPH方法模拟黏弹性流体,开发了OpenMP的并行CPU版本和CUDA的并行GPU版本,提高了数值模拟效率。Vahabi等[18]基于修正的弱可压缩SPH方法,对Giesekus模型的黏弹性流体中单个气泡的上升和变形进行了数值模拟。Moinfar等[19]通过弱可压缩SPH方法,基于Giesekus模型研究了黏弹性液滴变形问题。
对于注塑成型流动问题,也有一些学者利用SPH方法开展了相关的数值模拟。例如,Cleary等[20]基于SPH方法模拟了大型汽车铸件的注塑过程,很好地捕捉了流体运动和飞溅等关键信息。Vesenjak等[21]研究了SPH方法模拟黏性流体填充蜂窝结构的流动过程。Hou等[22]提出了压力边界技术,使用修正的SPH方法模拟了管道快速填充过程。Xu等[23]用改进的SPH方法研究了Cross黏性流体的三维Z形模具注塑成型问题,分析了注塑过程的流体变化情况。Robinson等[24]模拟了流体注入含有颗粒的圆柱形空腔过程,分析了注射流速和注射直径等工艺参数对颗粒分布的影响。He等[25]采用SPH方法研究了短纤维聚合物复合材料的三维注塑成型问题。上述研究工作表明,SPH方法可成功应用于注塑成型问题的数值模拟,但这些研究工作大多局限于注塑成型的宏观模拟。事实上,塑料制品的性能与熔体内部微观分子结构密切相关。目前,从微观分子结构角度对黏弹性注塑成型问题进行数值模拟的文献报道并不多见,因此探索注塑成型模拟的微宏观耦合计算方法、开展注塑成型过程的多尺度数值模拟具有重要的学术和应用价值。
本文基于珠-簧链模型,提出了一种多尺度SPH方法对黏弹性注塑成型过程进行数值模拟研究,并通过模拟黏弹性Couette流,验证了该方法的有效性。然后,将多尺度SPH方法扩展到C形腔和N形腔注塑成型问题,通过加密粒子间距和增加珠-簧链模型数量,验证了本文方法的数值收敛性。本研究展示了第一法向应力差、分子链拉伸量和构象厚度等成型过程中的微宏观物理信息,分析了分子链珠子数、最大拉伸量、溶剂黏度与总黏度之比、Reynolds数和Weissenberg数等流变参数对成型过程的影响。
1 控制方程在Lagrange坐标系中,等温黏弹性流体所涉及的质量和动量守恒方程分别为:
| $ \frac{\mathrm{d} \rho}{\mathrm{d} t}=-\rho \nabla \cdot \boldsymbol{u}, $ | (1) |
| $ \frac{\mathrm{d} \boldsymbol{u}}{\mathrm{d} t}=\frac{1}{\rho} \nabla \cdot \boldsymbol{\sigma}. $ | (2) |
其中:ρ是黏弹性流体的密度,t是时间,u是流体速度。σ是总应力张量,由压力p、黏性应力和弹性应力τ 3部分构成,
| $ \boldsymbol{\sigma}=-p \boldsymbol{I}+2 \eta_{\mathrm{s}} \boldsymbol{d}+\boldsymbol{\tau} . $ | (3) |
其中:I为单位矩阵,ηs为溶剂黏度。d为形变率张量,
| $ \boldsymbol{d}=\frac{1}{2}\left(\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right) . $ | (4) |
综合式(2)—(4),动量守恒方程可写为
| $ \frac{\mathrm{d} \boldsymbol{u}}{\mathrm{d} t}=-\frac{1}{\rho} \nabla p+\frac{\eta_{\mathrm{s}}}{\rho} \nabla^2 \boldsymbol{u}+\frac{1}{\rho} \nabla \cdot \boldsymbol{\tau} . $ | (5) |
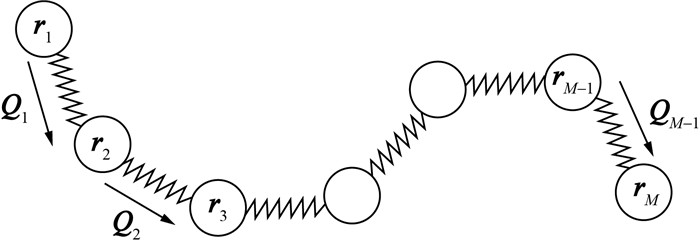
为了求解弹性应力τ,已有的研究[13, 18]通常采用本构方程进行计算。本文基于珠-簧链模型求解弹性应力,可以计算得到聚合物熔体内部的一些微观分子信息。一个流体粒子由Nb个珠-簧链模型组成,每一个珠-簧链模型由M-1个质量可忽略的弹簧和M个质量为mb的珠子组成,如图 1所示。弹簧用于描述聚合物分子链的弹性力,而珠子与分子链的黏性有关。为了更好地描述珠-簧链模型中的分子信息,引入构型向量Q,将第i和i +1个珠子之间的弹簧构型向量设为Qi=ri+1-ri(i=1, 2, …, M-1),其中ri(i=1, 2, …, M)为第i个珠子的位置向量。
|
| 图 1 珠-簧链模型 |
对珠-簧链模型的弹簧受力情况进行分析。构型向量Qi与分子链中每根弹簧所受的弹性约束 FiE相关,
| $ \overline{\boldsymbol{F}}_i^{\mathrm{E}}= \begin{cases}-2 \boldsymbol{F}_i+\boldsymbol{F}_{i+1}, & i=1 ; \\ \boldsymbol{F}_{i-1}-2 \boldsymbol{F}_i+\boldsymbol{F}_{i+1}, & i=2, 3, \cdots, M-2 ; \\ \boldsymbol{F}_{i-1}-2 \boldsymbol{F}_i, & i=M-1 .\end{cases} $ | (6) |
其中:Fi为珠-簧链模型中第i个和第i+1个珠子间弹簧所受的弹簧力。本文分别采用Hookean珠-簧链和有限拉伸非线性弹性(finitely extensible nonlinear elastic, FENE) 珠-簧链求解弹簧力Fi。Hookean模型和FENE模型中的弹簧力分别是线性和非线性的,并且前者等价于Oldroyd-B本构方程。两者的无量纲弹簧力分别表示为:
| $ \boldsymbol{F}_i(\boldsymbol{Q})=\boldsymbol{Q}_i, $ | (7) |
| $ \boldsymbol{F}_i(\boldsymbol{Q})=\frac{\boldsymbol{Q}_i}{1-\boldsymbol{Q}_i^2 / b} . $ | (8) |
其中:b=HQ02/(kBT)为无量纲最大拉伸长度的平方,H表示弹性常数,Q0为每段弹簧的最大拉伸长度,kB为Boltzmann常数,T为绝对温度。
在Brown构型场方法中,有相同初始构型且受到相同随机力的构型向量Qi形成一个构型场。Brown构型场方法基于Nb个连续构型向量Qi的变化来描述聚合物动力学行为。根据该方法,分子链模型的第i个构型向量Qi的演化方程可写为[26]
| $ \begin{gathered} \mathrm{d} \boldsymbol{Q}_i(\boldsymbol{x}, t)=\left[-\boldsymbol{u}(\boldsymbol{x}, t) \cdot \nabla \boldsymbol{Q}_i(\boldsymbol{x}, t)+\right. \\ \left.\boldsymbol{\kappa}(\boldsymbol{x}, t) \cdot \boldsymbol{Q}_i(\boldsymbol{x}, t)+\frac{1}{4 W i} \overline{\boldsymbol{F}}_i^{\mathrm{E}}\right] \mathrm{d} t+ \\ \sqrt{\frac{1}{2 W i}}\left(\mathrm{~d} \boldsymbol{W}_{i+1}(t)-\mathrm{d} \boldsymbol{W}_i(t)\right) . \end{gathered} $ | (9) |
其中 κ =(▽u)T为速度梯度的转置。Wi=λu/L为无量纲Weissenberg数,λ为珠-簧链模型的松弛时间,u为特征速度,L为特征长度。Wi表示Wiener过程的随机向量,其每个分量均是一个Gauss随机数。
对于珠-簧链模型构型场演化方程(9)的求解,采用三步半隐式校正算法[27]。该算法可以避免非物理解的出现,且有较好的计算稳定性和鲁棒性。根据Kramers表达式计算聚合物弹性应力,
| $ \boldsymbol{\tau}=\frac{1-\beta}{W i^*} \sum\limits_{j=1}^{M-1}\left(-\boldsymbol{I}+\frac{1}{N_{\mathrm{b}}}\left(\sum\limits_{i=1}^{N_{\mathrm{b}}} \boldsymbol{Q}_{i, j} \boldsymbol{F}\left(\boldsymbol{Q}_{i, j}\right)\right)\right) . $ | (10) |
其中:Wi*=Wi(M2-1)/(3+15/b),β表示溶剂黏度与总黏度之比。
1.2 状态方程对于弱可压缩SPH算法,流体压力通过状态方程中粒子密度的变化进行计算。本文采用的状态方程为[28]
| $ p(\rho)=c^2\left(\rho-\rho_0\right) \text {. } $ | (11) |
其中: ρ0为流体的初始密度,c为流体中的声速。在SPH方法中,声速值的选择非常重要: 声速值过小会导致压力波动,计算不稳定;过大会导致时间步长缩小,计算效率低。通常情况下,声速c一般取值为流体最大速度的10倍。本文使用弱可压缩SPH算法,在模拟过程中粒子质量保持不变,遵循质量守恒。
2 多尺度SPH方法 2.1 SPH离散SPH方法将流体域Ω离散成有限数量且均匀分布的粒子,其相关物理量通过插值近似来定义。对于任意函数f(x),以积分形式作插值近似,
| $ \langle f(\boldsymbol{x})\rangle=\int_{\mathit{\Omega }} f\left(\boldsymbol{x}^{\prime}\right) W\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}, h\right) \mathrm{d} \boldsymbol{x}^{\prime}. $ | (12) |
其中: 〈f(x)〉表示函数f(x)的近似估计,W(x-x′, h)为光滑函数,h是光滑长度,决定了光滑函数的影响域。同理,通过分部积分,可得▽f(x)的积分形式为
| $ \langle\nabla f(\boldsymbol{x})\rangle=-\int_{\mathit{\Omega }} f\left(\boldsymbol{x}^{\prime}\right) \nabla W\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}, h\right) \mathrm{d} \boldsymbol{x}^{\prime} . $ | (13) |
对积分表达式(13)进行粒子近似,将它转化为光滑函数影响域内的所有粒子叠加求和的离散形式。设粒子j在粒子i的支持域内,并且其质量为mj、密度为ρj以及函数值为f(xj),则式(12)和(13)的离散化粒子近似表达式可分别表示为:
| $ \left\langle f\left(\boldsymbol{x}_i\right)\right\rangle=\sum\limits_{j=1}^N \frac{m_j}{\rho_j} f\left(\boldsymbol{x}_j\right) W_{i j} \text {, } $ | (14) |
| $ \left\langle\nabla f\left(\boldsymbol{x}_i\right)\right\rangle=\sum\limits_{j=1}^N \frac{m_j}{\rho_j} f\left(\boldsymbol{x}_j\right) \nabla_i W_{i j} \text {. } $ | (15) |
本文采用五次样条光滑函数。该函数的二阶导数是连续的,从而保证了数值模拟具有良好的精度和计算稳定性[29]。五次样条函数的表达式为
| $ \begin{gathered} W(R, h)=\alpha_d \cdot \\ \begin{cases}(3-R)^5-6(2-R)^5+15(1-R)^5, & 0 \leqslant R <1 ; \\ (3-R)^5-6(2-R)^5, & 1 \leqslant R <2 ; \\ (3-R)^5, & 2 \leqslant R <3 ; \\ 0, & R \geqslant 3 .\end{cases} \end{gathered} $ | (16) |
其中:
在SPH方法中,为了保证粒子间的作用满足Newton第三定律的要求,通常需要将式(14)和(15)代入一些不同定义式进行适当的数学处理。由此,可推导出质量和动量守恒方程多种不同的离散格式。对于质量守恒方程,常用离散格式之一为[30]
| $ \left(\frac{\mathrm{d} \rho}{\mathrm{d} t}\right)_i=\sum\limits_j m_j\left(\boldsymbol{u}_i-\boldsymbol{u}_j\right) \nabla_i W_{i j} . $ | (17) |
该格式为反对称离散格式,能够降低由粒子的非连续性产生的误差。
对于动量守恒方程中的压力梯度项和弹性应力项,通常采用对称离散格式,使线性动量和角动量保持精确守恒。对于黏性项,采用Shao和Lo[31]提出的离散格式。由此,动量守恒方程的SPH离散格式最终写为
| $ \begin{gathered} \left(\frac{\mathrm{d} \boldsymbol{u}}{\mathrm{d} t}\right)_i=\sum\limits_j m_j\left(-\left(\frac{p_i}{\rho_i^2}+\frac{p_j}{\rho_j^2}\right) \nabla_i W_{i j}+\right. \\ \left.\frac{8 \eta_{\mathrm{s}}}{\left(\rho_i+\rho_j\right)^2} \frac{\boldsymbol{r}_{i j} \cdot \nabla_i W_{i j}}{\left|\boldsymbol{r}_{i j}\right|^2+\varphi^2}\left(\boldsymbol{u}_i-\boldsymbol{u}_j\right)+\left(\frac{\boldsymbol{\tau}_{p, i}}{\rho_i^2}+\frac{\boldsymbol{\tau}_{p, j}}{\rho_i^2}\right) \nabla_i W_{i j}\right) . \end{gathered} $ | (18) |
rij表示为粒子i的位置向量与粒子j的位置向量的差。此外,对于式(4)中速度梯度和式(9)中构型场梯度的SPH离散,本文使用如下的反对称离散格式:
| $ \left(\frac{\partial A}{\partial x}\right)_i=\sum\limits_j \frac{m_j}{\rho_j}\left(A_j-A_i\right) \frac{\partial W_{i j}}{\partial x_i}, $ | (19) |
| $ \left(\frac{\partial A}{\partial y}\right)_i=\sum\limits_j \frac{m_j}{\rho_j}\left(A_j-A_i\right) \frac{\partial W_{i j}}{\partial y_i} . $ | (20) |
其中A表示速度u或构型向量Q在x、y方向的分量。
2.2 珠-簧链模型的分子信息传统的宏观方法通常采用本构方程来描述流体的黏弹性行为,然而宏观本构方程中的参数大多是经验参数,很难从机理上解释熔体分子结构对宏观流动的影响。本文使用珠-簧链模型对黏弹性注塑成型过程进行数值模拟,可计算得到传统宏观方法所不能获得的一些微观分子信息。除了对成型过程中的第一法向应力差进行分析外,本文特别提取了成型过程中的分子链拉伸量和分子链构象厚度,并进行了可视化。
分子链拉伸量S的定义为沿主流方向上珠子与珠子之间的最大长度,即分子链在流动方向上的投影长度。于是,单个分子链拉伸量S的计算公式[32]可写为
| $ \bar{S}=\max \left(r_{i, x}\right)-\min \left(r_{i, x}\right) . $ | (21) |
其中ri, x是珠子i沿x方向的位置。对S进行系综平均,得到稳态分子链拉伸量,
| $ S=\frac{1}{M} \sum\limits_{n=1}^M \bar{S}_n. $ | (22) |
分子链构象厚度δy的定义为分子链在速度梯度方向上的厚度,通常用于检测分子链在运动过程中是否存在自由旋转。为了计算δy,先定义回旋半径张量[32]G为
| $ \boldsymbol{G}=\frac{1}{2 M^2}\left[\sum\limits_{i=1}^M \sum\limits_{j=1}^M\left(\boldsymbol{r}_i-\boldsymbol{r}_j\right)\left(\boldsymbol{r}_i-\boldsymbol{r}_j\right)\right] . $ | (23) |
分子链构象厚度δy计算公式为[32]
| $ \delta_y=\sqrt{G_{y y}} \text {. } $ | (24) |
其中Gyy是回旋半径张量G在y方向上的分量。
2.3 珠-簧链模型的参数选择对于不同珠子数的珠-簧链模型,它们之间的等价关系可用最大拉伸量(长度尺度)和特征松弛时间(时间尺度)来表示。
对于含有M个珠子的珠-簧链模型,每根弹簧的最大拉伸长度可表示为
| $ b=\frac{b_{\max }}{M-1}, $ | (25) |
其中bmax是FENE珠-簧链的最大拉伸量。
特征松弛时间λ的定义为
| $ \lambda=\frac{\lambda^*}{a}. $ | (26) |
其中:
| $ a=\left(\frac{b_{\max }+7}{15 b_{\max }}\right)\left(\frac{b}{b+5}\right)\left(\left(2 M^2+7\right)-\frac{12\left(M^2+1\right)}{M(b+7)}\right), $ | (27) |
λ*表示与具有M个珠子的珠-簧链模型等价的哑铃特征松弛时间。
此外,为了提高SPH方法的计算精度,本文在求解控制方程时,采用了核梯度修正技术[33-34]。同时,对于固壁边界的处理,本文采用了由边界粒子和虚拟粒子两类粒子组成的增强型边界处理技术。关于核梯度修正和增强型边界处理技术的更多内容,可参阅本文作者之前的研究工作[35]。
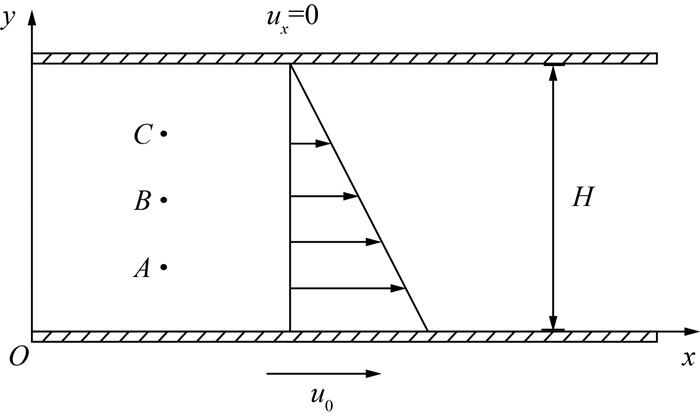
3 数值算例与分析 3.1 Couette流为了验证多尺度SPH方法的有效性,首先对黏弹性Couette流进行模拟。图 2给出了该问题的计算模型。流体位于两块无限大的平板之间,两平板的距离设置为H=1 m。在初始时刻,流体和平板均是静止的;当t>0 s时,下平板突然以恒定速度u0=1 m·s-1沿x轴正方向运动。运动过程中,相同y坐标的流体运动情况相同,因此左右边界施加周期边界条件。于是,平板长度可取为L=1 m。为了更好地分析数值模拟中流动物理量随时间的演变,选取A、B和C 3点,它们到下平板的距离分别为0.25H、0.5H和0.75H。
|
| 图 2 黏弹性Couette流的计算模型 |
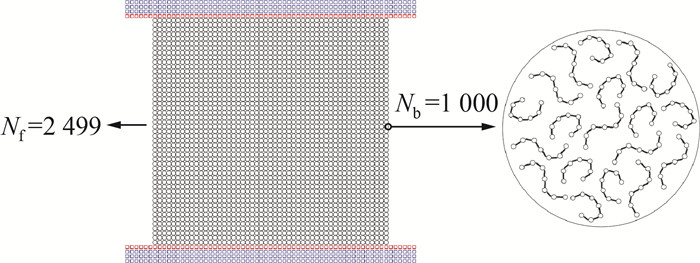
研究过程中,根据弹簧力和珠子数的不同,由简入繁,逐步进行模拟。首先考虑珠子数M=2和弹簧力是线性的模型,即Hookean哑铃模型。该模型等价于Oldroyd-B本构模型,因此对于该问题,存在速度的解析解用于验证算法的有效性。模拟过程中,流体密度ρ=1.0 kg·m-3,Reynolds数Re=ρuL/η=1.5, Weissenberg数Wi=λu/L=10.0,溶剂黏度与总黏度之比β=0.1。粒子初始间距Δx=0.02 m,光滑长度h=1.3Δx,时间步长Δt=1.0×10-4 s。对于该问题的微宏观耦合计算,图 3给出了Couette流的粒子分布示意图,其中使用了Nf=2 499个流体粒子,而每个流体粒子中包含Nb=1 000个珠-簧链模型。
|
| 图 3 黏弹性Couette流的粒子分布和珠-簧链模型示意图 |
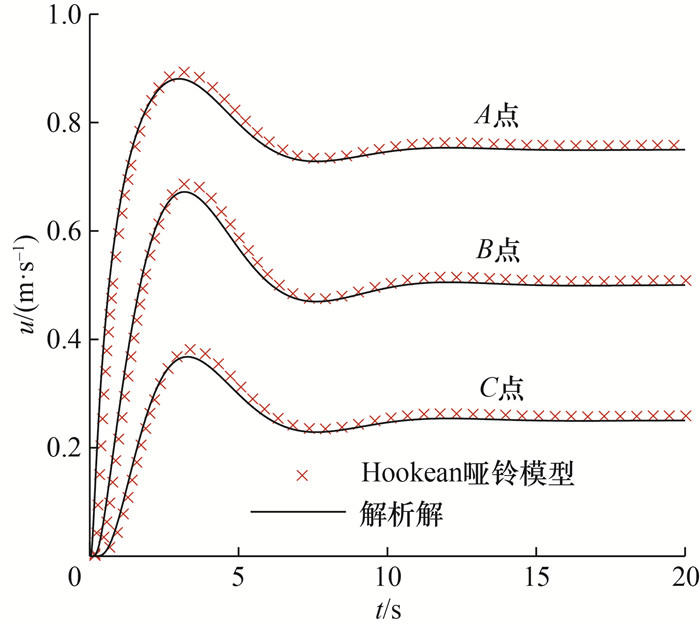
图 4展示了速度u水平分量在A、B、C 3个监测点处随时间的变化情况,并将SPH结果与解析解进行了比较。由图 4可见,两者吻合较好,验证了本文提出的多尺度SPH方法模拟黏弹性流体流动问题的有效性。此外,流体的弹性作用引起了速度过冲现象。越靠近下平板的流体,其流动速度越大,并且越接近于下平板移动速度。
|
| 图 4 基于Hookean哑铃模型的黏弹性Couette流的SPH数值解与解析解的比较 |
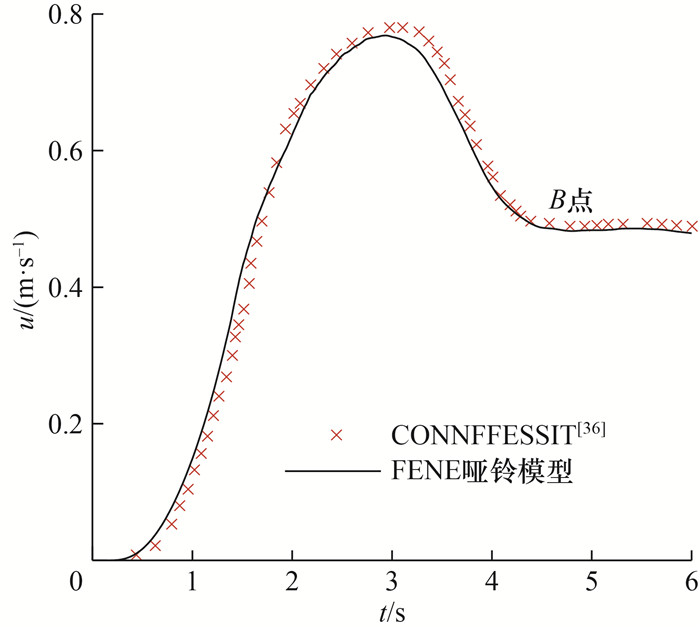
接着,考虑珠子数M=2和弹簧力是非线性的模型,即FENE哑铃模型。对于该问题,Laso和Ottinger[36]基于CONNFFESSIT方法使用了50 000个哑铃数目进行了模拟。为了验证所提算法的有效性,本文使用和文[36]相同的物理参数,即ρ=1.275 7 kg·m-3,Re=1.275 7,Wi=49.62,β=0.052 1。FENE哑铃模型中弹簧的最大拉伸长度设置为bmax=50,而其余参数均保持与Hookean哑铃模型相同。可见,由于本文使用了系综平均技术计算弹性应力,因此能够使用比文[36]更少的哑铃数目,得到精确稳定的弹性应力。
图 5展示了本文多尺度SPH方法和CONNFFESSIT方法模拟Couette流在B点处的速度u水平分量随时间的变化情况。可以看出,B点处的速度先增大后减小,存在明显的速度过冲现象。本文多尺度SPH方法很好地捕捉到了黏弹性流体的复杂流变特性。同时,计算结果与文[36]基本一致,进一步验证了本文方法的有效性。
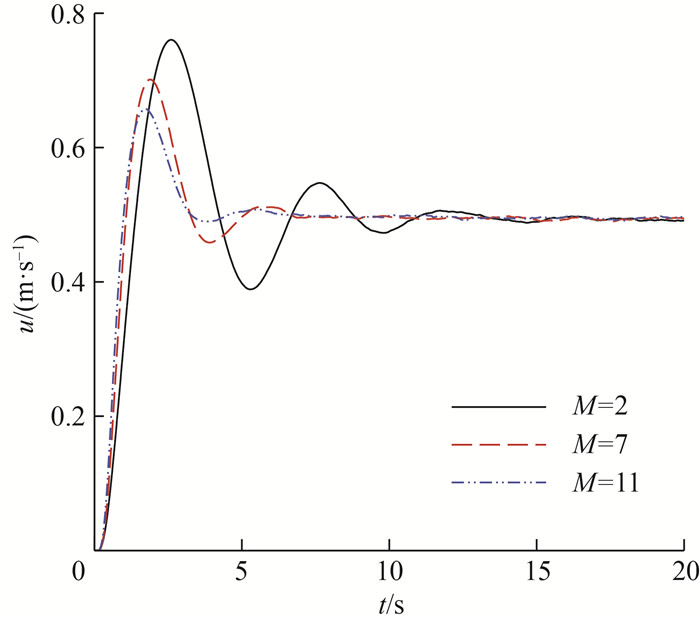
最后,扩展到FENE链模型进行模拟。相较于Hookean和FENE哑铃模型,FENE链模型在一定程度上克服了哑铃模型相对粗糙、不能模拟较宽时间尺度流动问题的缺陷。加之,FENE链模型能够更形象地描述大分子链在流场中的运动状态(如链的拉伸和翻滚等行为),因此能够更加合理地预测聚合物溶液的复杂流变特性。在模拟过程中,各物理参数分别取值如下:ρ=1.0 kg·m-3,Re=1.5,Wi=10.0,β=0.1,Δx=0.02 m,h=1.3Δx。每根弹簧的拉伸量设置为b=50。同时,为了观察不同珠子数对黏弹性流体流动过程的影响,选用M=2、7和11这3种不同数量的珠子数进行模拟。图 6给出了B点处计算得到的速度随时间的变化情况。可以看出,B点处的速度先增大后减小,表明对于复杂的FENE链模型,本文多尺度SPH方法依然能够很好地捕捉黏弹性流体特有的速度过冲现象。另外,M值越小,发生速度过冲现象越延迟,达到稳态所需的时间越长,过冲趋势也越明显。尤其M=2的流动情形,可以观察到多次明显的速度过冲现象。随M值增大,速度波动变化逐渐减小。特别是,M=7与11的流动行为几乎相同,表明使用M=7已经能够合理地描述黏弹性流体的复杂流变特性。总之,本文多尺度SPH方法能够很好地预测黏弹性流体的速度过冲现象,验证了算法的有效性。
|
| 图 6 不同珠子数M模拟时B点处的速度变化 |
3.2 C形腔注塑成型
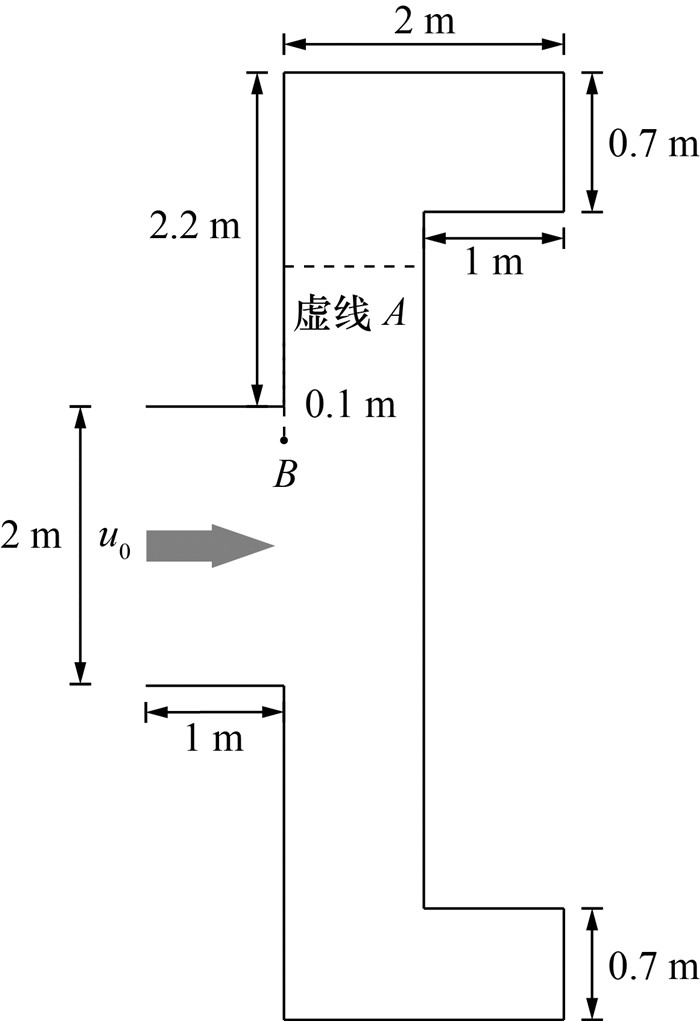
应用多尺度SPH方法对二维C形腔黏弹性注塑成型问题进行数值模拟。图 7描述了该问题的几何模型。在注塑过程中,有一个注射入口,其宽度L=2 m。注入速度u0=1 m·s-1,熔体密度ρ=1 000 kg·m-3。各无量纲参数取值为:Re=2,Wi=0.2,β=0.5。在入口横截面方向布置49层流体粒子,此时初始粒子间距为Δx=0.04 m。当空腔完全填充时,SPH流体粒子总数为Nf=9 849。在本例中,采用FENE链模型(M=7),最大拉伸量为bmax=300。每个粒子中的珠-簧链模型数为Nb=1 000。光滑长度h=1.3Δx,时间步长Δt=2.5×10-5 s。
|
| 图 7 C形腔注塑成型的计算模型 |
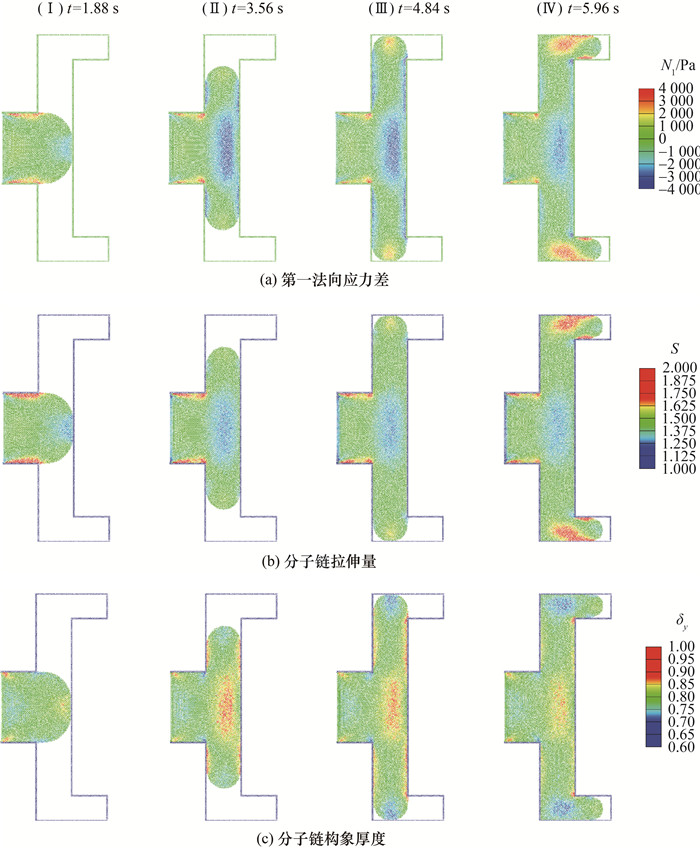
由于本文基于FENE链模型对C形腔注塑成型问题进行模拟研究,因此不仅可以得到成型过程中的第一法向应力差等宏观物理信息,还可得到聚合物的分子链拉伸量和构象厚度等微观分子信息。图 8展示了t=1.88 s、3.56 s、4.84 s和5.96 s 4个时刻的第一法向应力差、分子链拉伸量和构象厚度变化情况。可以看到,熔体刚开始从入口缓慢注入,在水平管道内向右移动。在t=1.88 s时刻,熔体触碰右壁。之后水平管腔内熔体分成两部分,沿右侧竖直管道上下流动。在t=4.84 s时刻,上下熔体分支分别触碰到上下水平腔壁,之后两个熔体分支继续沿管道向右流动。随着熔体继续注入,整个C形腔被完全填充。图 8a展示了第一法向应力差随熔体流动的变化情况。可以看到,入口水平管道中,靠近上下水平腔壁处的熔体第一法向应力差较大。之后熔体触碰到右壁后,熔体逐渐被压缩,该处的第一法向应力差绝对值增大。在竖直管道中,靠近腔壁的熔体,第一法向应力差绝对值较大,其方向与正方向相反。随着C形腔填充完毕,在水平分支管道中,靠近上下水平腔壁的第一法向应力差较大,方向为正。图 8b为分子链拉伸量随熔体流动的变化情况。随着熔体注入空腔,熔体内的珠-簧链一直存在拉伸行为,并且入口水平管道中的熔体离上下腔壁越近,拉伸量越大。在t=1.88 s时刻,熔体触碰到右壁后,靠近腔壁的黏弹性熔体分子链被压缩,拉伸量减小。之后,分支触碰上下腔壁向右流动,弯角外侧有强烈的拉伸现象,此时靠近腔壁的熔体分子链拉伸量增大。图 8c为熔体的分子链构象厚度变化情况。最初熔体注入时,熔体前端以及靠近入口腔壁处的分子链构象厚度较大。水平流动的熔体接触右腔壁后,构象厚度突然增大。随着上下分支继续注入,靠近腔壁两侧的熔体分子链构象厚度较大。
|
| 图 8 C形腔黏弹性注塑成型的多尺度SPH模拟 |
3.2.1 算法收敛性
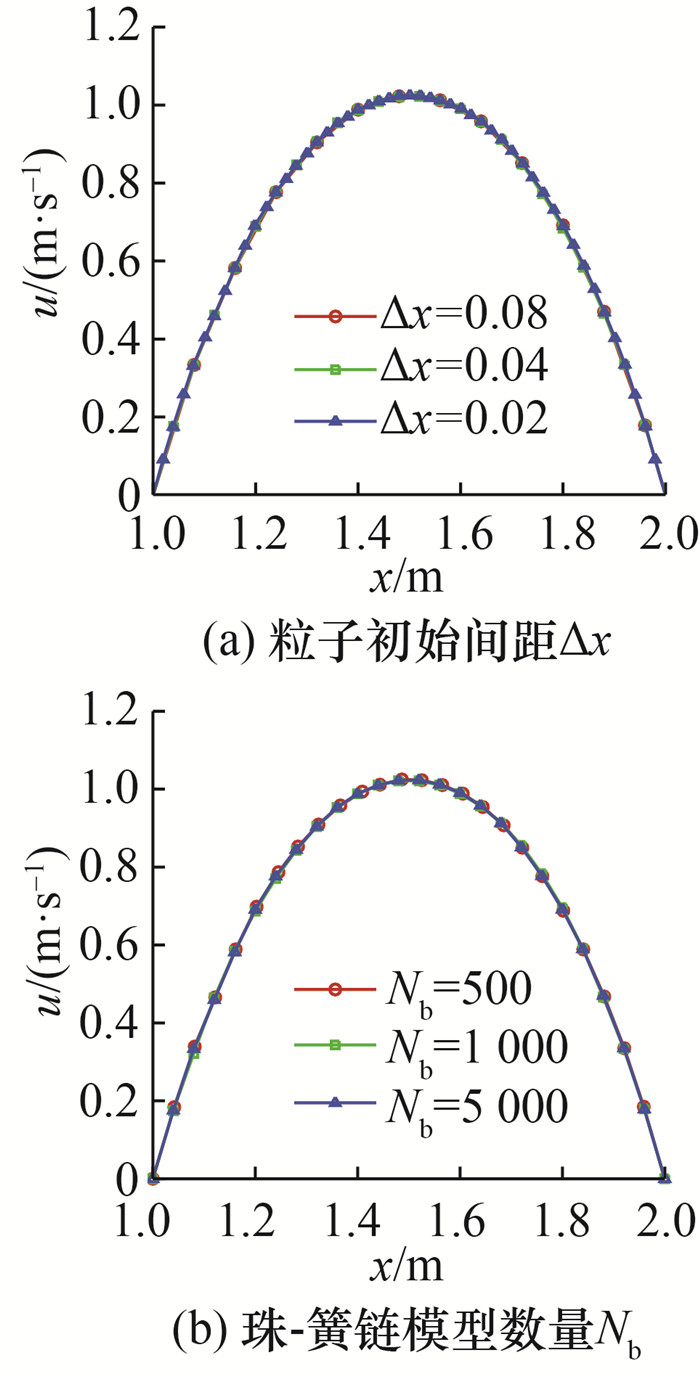
目前,尚未见到应用其他数值方法对黏弹性注塑成型问题进行微宏观模拟的文献报道。因此,本文通过评价多尺度SPH方法模拟C形腔黏弹性注塑成型过程的数值收敛性,来验证算法的准确性和有效性。具体来讲,本文通过更改SPH流体粒子数Nf(宏观尺度)和每个粒子中的珠-簧链模型数Nb(微观尺度)来核验SPH数值解的变化。对于Nf,分别采用3种不同的粒子初始间距,即Δx=0.08、0.04和0.02 m进行计算。这3种粒子间距对应SPH流体粒子总数分别为Nf=3 509、9 849和39 699。对于Nb,分别采用Nb=500、1 000和5 000,其他物理参数保持不变。在研究过程中,为了定量地评估黏弹性注塑成型过程多尺度算法的数值收敛性,提取了t=4.5 s时刻熔体上分支沿竖直管道向上流动的速度分布(见图 7中的虚线A)。如图 9所示,无论是用3种不同的粒子初始间距Δx,还是用3种不同的珠-簧链模型数Nb,计算得到的虚线A处的熔体速度均大致相同,表明本文多尺度SPH方法的数值收敛性良好。
|
| 图 9 t=4.5 s时竖直通道的速度分布变化情况 |
3.2.2 流变参数对流动的影响
由于所用SPH流体粒子数Nf和珠-簧链模型数Nb越多,模拟时间越长,因此对于后续的模拟,本文使用Nf=9 849和Nb=1 000进行计算。
1) 珠子数M对流动的影响。
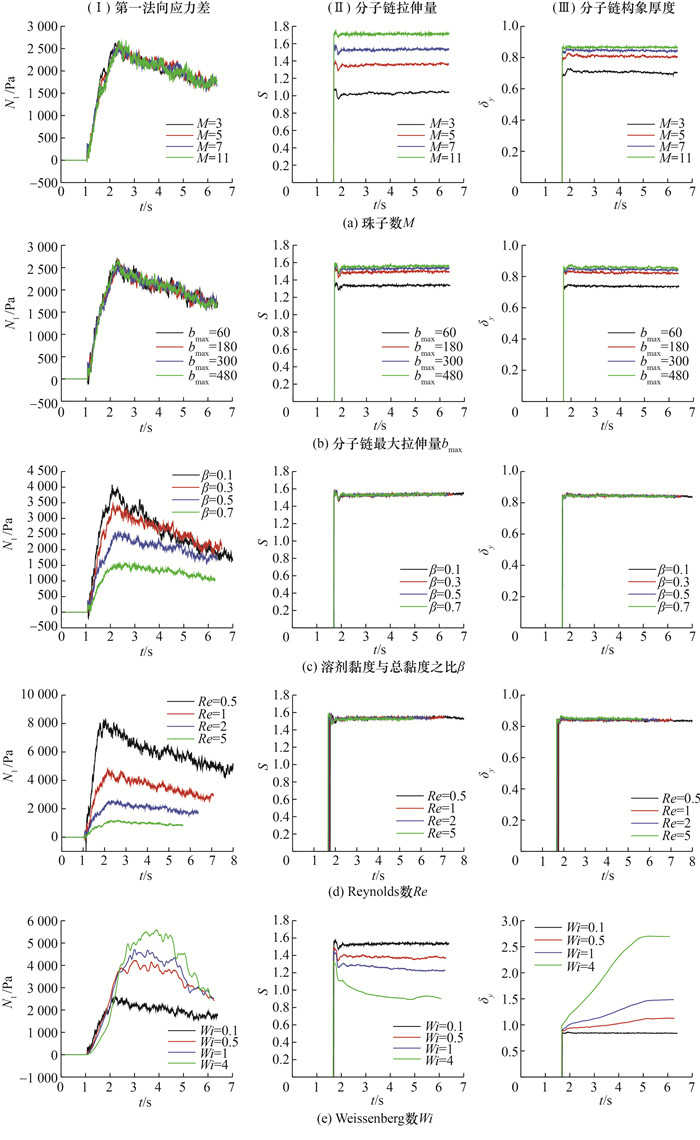
为了研究珠子数M对C形腔各分子信息的变化趋势的影响,分别考虑了M=3、5、7和11时的4种情况。图 10a展示了图 7中的B点处不同珠子数M的微宏观信息随时间变化情况。可以看出,M越大,第一法向应力差波动越剧烈,但不同M获得的第一法向应力差的变化趋势几乎一致,这表明珠子数M对第一法向应力差的影响不大。对于微观分子信息,随着M的增大,分子链拉伸量和分子链构象厚度均增大。这是因为M越大,分配给每根弹簧上的拉伸量越大,导致分子链拉伸量越大,而分子链的长度越长,构象厚度也越大。
|
| 图 10 不同流变参数对流动的影响 |
2) 最大拉伸量bmax对流动的影响。
图 10b显示了最大拉伸量bmax对C形腔各分子信息变化趋势的影响,分别考虑了每根弹簧的拉伸量b=10、30、50和80。珠子数M取值为7,对应珠-簧链模型的最大拉伸量分别为bmax=60、180、300和480的4种情况。可以看出,不同bmax对第一法向应力差的影响很小,可以忽略不计。bmax变化对分子链拉伸量和构象厚度的影响较大。bmax越大,达到稳态的分子链拉伸量和构象厚度越大,但是两者的变化增量均逐渐减小。
3) 溶剂黏度与总黏度之比β对流动的影响。
溶剂黏度与总黏度之比β对C形腔各分子信息的影响如图 10c所示,分析了β=0.1、0.3、0.5和0.7的4种情况。不同β值对第一法向应力差的影响较大。β值越大,第一法向应力差的最大值越小,并且达到峰值之后下降幅度越小。这是因为溶剂黏度与总黏度之比β越大,溶剂黏度越大,流体越近似于Newton流体,弹性越小,因此第一法向应力差过冲现象越弱。不同β值对分子链拉伸量和构象厚度的影响则非常小,这表明β不是影响微观分子信息变化的主要原因。
4) Reynolds数(Re)对流动的影响。
为分析Re对C形腔各分子信息的变化趋势的影响,分别考虑了Re=0.5、1、2和5时的4种情况。图 10d给出了不同Reynolds数在B点处的微宏观信息随时间变化情况。Re越大,C形腔填充完毕所需时间越短。可以看出,第一法向应力差受到Re的影响。Re越大,第一法向应力差达到的峰值越小,达到峰值所需时间越长,并且达到峰值之后下降幅度越小,即随着Re增大,第一法向应力差过冲现象越弱。该现象可以解释为Re越大,流体黏性力影响越弱,聚合物黏度也越弱,因此第一法向应力差也越小。Re对分子链拉伸量和构象厚度的影响很小,采用不同Re计算得到的微观分子信息几乎相同。
5) Weissenberg数Wi对流动的影响。
图 10e给出了不同Weissenberg数Wi在B点处的微宏观信息随时间变化情况,分别考虑了Wi=0.1、0.5、1和4时的4种情况。Wi越大,C形腔填充完毕所需时间越短,但是相较Re,Wi对时间的影响较小。可以看出,Wi越大,第一法向应力差的峰值越大,达到峰值的时间越长,达到峰值之后下降幅度越大,并且数值振荡越紊乱。另外,随着Wi增大,分子链拉伸量越小,甚至当Wi=4时,出现了数值不稳定现象。这是由于Wi越大,其黏性作用越弱,存在剪切变稀现象,因此分子链拉伸量越小。Wi对分子链构象厚度也有显著的影响,即Wi值越大,分子链构象厚度越大,上升幅度越明显,达到稳态所需时间越长。
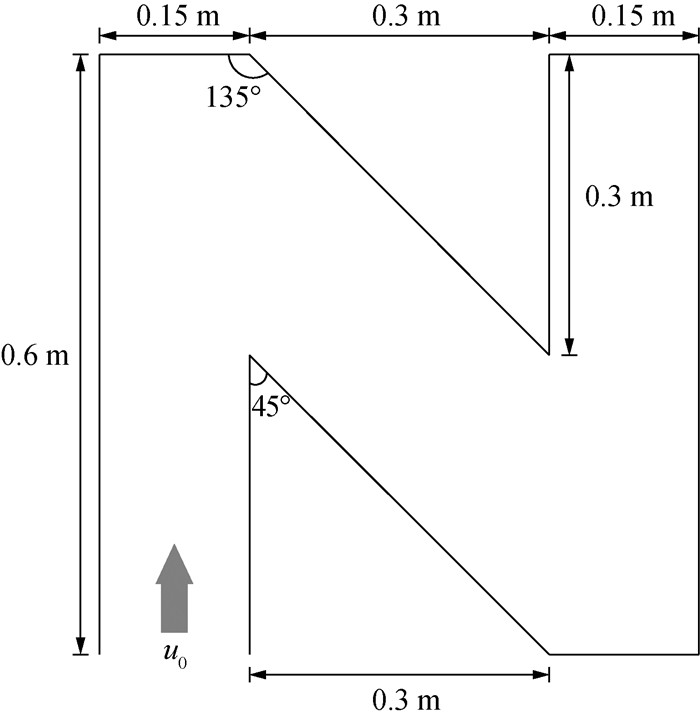
3.3 N形腔注塑成型本文选取的最后一个数值算例是N形腔黏弹性注塑成型。该问题的几何模型如图 11所示。模型左下方有一个宽度L=0.15 m的注射口。熔体密度ρ=1 000 kg·m-3,注入速度u0=1 m·s-1。Reynolds数、Weissenberg数和溶剂黏度比分别设置为Re=7.5、Wi=13、β=0.5。初始粒子间距设置为Δx=0.003 m,此时沿注射入口横截面有49个流体粒子,因此用于完全填充空腔的SPH流体粒子数量为Nf= 39 249,固壁粒子和虚粒子的数量分别为1 033和11 798。为保持数值稳定,时间步长设置为Δt=2.0× 10-5 s,光滑长度取h=1.3Δx。选用FENE珠-簧链进行计算,珠-簧链的最大拉伸量为bmax=300。
|
| 图 11 N形腔注塑成型的计算模型 |
图 12显示了5个不同时刻t=0.3、0.66、0.9、1.64和2.0 s下的N形腔黏弹性注塑成型的第一法向应力差、分子链拉伸量和构象厚度的分布。最初,熔体以稳定的注射速度从左下入口缓慢注入。注入初期,熔体沿腔壁向上移动。在t=0.66 s时刻,熔体到达左侧水平腔顶。由于熔体具有黏弹性,即使右边没有腔壁,熔体只是向右边轻微倾斜。熔体将左上方空腔填充完毕之后沿着上部倾斜腔壁向右下方移动。随着填充继续,熔体触碰到右侧垂直腔壁,之后填充右下方空腔。右下方空腔填充完毕后,熔体沿右侧垂直管道向上移动,最终将整个空腔填充完毕。从图 12a中可以看到,左侧竖直管道处,熔体越靠近左右腔壁,第一法向应力差绝对值越大。之后随着熔体的不断填充,左上方空腔和倾斜管道拐角处的第一法向应力差较大。图 12b显示,注入初期,熔体前端和靠近入口腔壁处的分子链拉伸量较大。之后,熔体前端的拉伸量越来越大。在t=0.9 s时,熔体将左上方空腔填充完全。t=1.64 s时刻,熔体填充到右下方空腔,倾斜管道内填充完毕,此时左上方空腔中心处的分子链拉伸量较大,同时靠近倾斜管道下部腔壁的分子链拉伸量较大。如图 12c所示,熔体沿着左侧竖直管道流动时,靠近左右腔壁的熔体分子链构象厚度较大,管道中间的熔体构象厚度较小。填充完毕后,倾斜管道上部腔壁附近和右侧竖直管道右侧腔壁附近的熔体构象厚度较大,其值约为1.25,而左上方空腔顶端的熔体构象厚度一直较小。

|
| 图 12 N形腔黏弹性注塑成型的多尺度SPH模拟 |
4 结论
本文提出了一种多尺度SPH方法,宏观尺度上基于SPH方法求解控制方程,微观尺度上基于Brown构型场的珠-簧链模型求解弹性应力,并且开展了不同注塑形状的模拟实验,展示了注塑过程中的微宏观物理信息,分析了不同流变参数的变化规律。主要结论如下:
1) 对于黏弹性Couette流的多尺度SPH模拟,选用3种珠-簧链模型进行计算,并将SPH数值解与解析解或文献结果进行比较,结果表明本文所提出的多尺度SPH方法求解黏弹性流动问题是准确且有效的。
2) 构建了C形腔和N形腔黏弹性注塑成型模型,开展了相应的多尺度SPH模拟研究。使用不同粒子初始间距和珠-簧链模型数量进行计算,表明本文所提出的多尺度SPH方法求解注塑成型问题是数值收敛的。另外,深入讨论了不同流变参数对微宏观物理信息的影响,发现:M和bmax越大,分子链拉伸量和构象厚度的稳态值越大;β和Re越大,第一法向应力差达到的峰值越小,过冲现象越弱;Wi越大,第一法向应力差峰值越大,数值越震荡,分子链拉伸量越小,分子链构象厚度越大。
3) 本文所提出的多尺度SPH方法能够稳定、准确地模拟黏弹性注塑成型过程,同时能够计算得到传统宏观方法无法获得的一些微观分子信息,为黏弹性注塑成型过程的多尺度模拟研究提供了一种新的研究思路和方法。
| [1] |
LI X J, HE J H. Variational multi-scale finite element method for the two-phase flow of polymer melt filling process[J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2020, 30(3): 1407-1426. DOI:10.1108/HFF-07-2019-0599 |
| [2] |
QUAGLIATO L, LEE J, FONSECA J H, et al. Influences of stress triaxiality and local fiber orientation on the failure strain for injection-molded carbon fiber reinforced polyamide-6[J]. Engineering Fracture Mechanics, 2021, 250: 107784. DOI:10.1016/j.engfracmech.2021.107784 |
| [3] |
XIONG M X, WANG Y H, LIEW J Y R. Evaluation on thermal behavior of concrete-filled steel tubular columns based on modified finite difference method[J]. Advances in Structural Engineering, 2016, 19(5): 746-761. DOI:10.1177/1369433215622864 |
| [4] |
RANADE R, HILL C, PATHAK J. DiscretizationNet: A machine-learning based solver for Navier-Stokes equations using finite volume discretization[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 378: 113722. DOI:10.1016/j.cma.2021.113722 |
| [5] |
GUO Q, RUI H X, LI X L. Modified marker and cell schemes for Stokes equations with Dirichlet boundary condition[J]. Mathematical Methods in the Applied Sciences, 2022, 45(16): 10384-10407. DOI:10.1002/mma.8374 |
| [6] |
魏建国, 韩江, 侯庆志, 等. 声道中气动声学问题的光滑粒子动力学模拟[J]. 清华大学学报(自然科学版), 2016, 56(11): 1242-1248. WEI J G, HAN J, HOU Q Z, et al. SPH simulations of aeroacoustic problems in vocal tracts[J]. Journal of Tsinghua University (Science and Technology), 2016, 56(11): 1242-1248. (in Chinese) |
| [7] |
LUCY L B. A numerical approach to the testing of the fission hypothesis[J]. Astronomical Journal, 1977, 82: 1013-1024. DOI:10.1086/112164 |
| [8] |
GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3): 375-389. DOI:10.1093/mnras/181.3.375 |
| [9] |
MONAGHAN J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics, 1994, 110(2): 399-406. DOI:10.1006/jcph.1994.1034 |
| [10] |
ELLERO M, TANNER R I. SPH simulations of transient viscoelastic flows at low Reynolds number[J]. Journal of Non-Newtonian Fluid Mechanics, 2005, 132(1-3): 61-72. DOI:10.1016/j.jnnfm.2005.08.012 |
| [11] |
LIU M B, LIU G R. Smoothed particle hydrodynamics (SPH): An overview and recent developments[J]. Archives of Computational Methods in Engineering, 2010, 17(1): 25-76. DOI:10.1007/s11831-010-9040-7 |
| [12] |
GHYSELS P, SAMAEY G, VAN LIEDEKERKE P, et al. Multiscale modeling of viscoelastic plant tissue[J]. International Journal for Multiscale Computational Engineering, 2010, 8(4): 379-396. DOI:10.1615/IntJMultCompEng.v8.i4.30 |
| [13] |
HASHEMI M R, FATEHI R, MANZARI M T. SPH simulation of interacting solid bodies suspended in a shear flow of an Oldroyd-B fluid[J]. Journal of Non-Newtonian Fluid Mechanics, 2011, 166(21-22): 1239-1252. DOI:10.1016/j.jnnfm.2011.08.002 |
| [14] |
VÁZQUEZ-QUESADA A, ELLERO M. SPH simulations of a viscoelastic flow around a periodic array of cylinders confined in a channel[J]. Journal of Non-Newtonian Fluid Mechanics, 2012, 167-168: 1-8. DOI:10.1016/j.jnnfm.2011.09.002 |
| [15] |
BAO Y D, WU D M. Virtual training system with physical viscoelastic model and blood flow simulation based on a range-based SPH method[J]. Journal of Biomimetics, Biomaterials and Biomedical Engineering, 2015, 25: 41-53. DOI:10.4028/www.scientific.net/JBBBE.25.41 |
| [16] |
HECK T, SMEETS B, VANMAERCKE S, et al. Modeling extracellular matrix viscoelasticity using smoothed particle hydrodynamics with improved boundary treatment[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 322: 515-540. DOI:10.1016/j.cma.2017.04.031 |
| [17] |
DOS SANTOS BRITO C J, VIEIRA-E-SILVA A L B, ALMEIDA M W S, et al. Large viscoelastic fluid simulation on GPU [C]//2017 16th Brazilian Symposium on Computer Games and Digital Entertainment (SBGames). Curitiba, Brazil: IEEE, 2017: 134-143.
|
| [18] |
VAHABI M, KAMKARI B. Simulating gas bubble shape during its rise in a confined polymeric solution by WC-SPH[J]. European Journal of Mechanics-B/Fluids, 2019, 75: 1-14. DOI:10.1016/j.euromechflu.2018.12.003 |
| [19] |
MOINFAR Z, VAHABI S, VAHABI M. Numerical simulation of drop deformation under simple shear flow of Giesekus fluids by SPH[J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2023, 33(1): 263-281. DOI:10.1108/HFF-01-2022-0067 |
| [20] |
CLEARY P W, HA J, PRAKASH M, et al. 3D SPH flow predictions and validation for high pressure die casting of automotive components[J]. Applied Mathematical Modelling, 2006, 30(11): 1406-1427. DOI:10.1016/j.apm.2006.03.012 |
| [21] |
VESENJAK M, REN Z. Application aspects of the meshless SPH method[J]. Journal of the Serbian Society for Computational Mechanics, 2007, 1(1): 74-86. |
| [22] |
HOU Q, ZHANG L X, TIJSSELING A S, et al. Rapid filling of pipelines with the SPH particle method[J]. Procedia Engineering, 2012, 31: 38-43. |
| [23] |
XU X Y, OUYANG J, YANG B X, et al. SPH simulations of three-dimensional non-Newtonian free surface flows[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 256: 101-116. DOI:10.1016/j.cma.2012.12.017 |
| [24] |
ROBINSON M, LUDING S, RAMAIOLI M. SPH-DEM simulations of grain dispersion by liquid injection[J]. AIP Conference Proceedings, 2013, 1542(1): 1122-1125. |
| [25] |
HE L P, LU G, CHEN D C, et al. Three-dimensional smoothed particle hydrodynamics simulation for injection molding flow of short fiber-reinforced polymer composites[J]. Modelling and Simulation in Materials Science and Engineering, 2017, 25(5): 055007. DOI:10.1088/1361-651X/aa6dc9 |
| [26] |
XU X Y, YU P. A multiscale SPH method for simulating transient viscoelastic flows using bead-spring chain model[J]. Journal of Non-Newtonian Fluid Mechanics, 2016, 229: 27-42. DOI:10.1016/j.jnnfm.2016.01.005 |
| [27] |
KAILASHAM R, CHAKRABARTI R, PRAKASH J R. Shear viscosity for finitely extensible chains with fluctuating internal friction and hydrodynamic interactions[J]. Journal of Rheology, 2023, 67(1): 105-123. DOI:10.1122/8.0000498 |
| [28] |
SUN P N, PILLOTON C, ANTUONO M, et al. Inclusion of an acoustic damper term in weakly-compressible SPH models[J]. Journal of Computational Physics, 2023, 483: 112056. DOI:10.1016/j.jcp.2023.112056 |
| [29] |
MUTA A, RAMACHANDRAN P. Efficient and accurate adaptive resolution for weakly-compressible SPH[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 395: 115019. DOI:10.1016/j.cma.2022.115019 |
| [30] |
XU X Y, OUYANG J, LI W M, et al. SPH simulations of 2D transient viscoelastic flows using Brownian configuration fields[J]. Journal of Non-Newtonian Fluid Mechanics, 2014, 208-209: 59-71. DOI:10.1016/j.jnnfm.2014.04.005 |
| [31] |
SHAO S D, LO E Y M. Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface[J]. Advances in Water Resources, 2003, 26(7): 787-800. DOI:10.1016/S0309-1708(03)00030-7 |
| [32] |
BONVIN J C. Numerical simulation of viscoelastic fluids with mesoscopic models [D]. Lausanne, Switzerland: EPFL, 2000.
|
| [33] |
LIU M B, LIU G R. Restoring particle consistency in smoothed particle hydrodynamics[J]. Applied Numerical Mathematics, 2006, 56(1): 19-36. DOI:10.1016/j.apnum.2005.02.012 |
| [34] |
LIU M B, SHAO J R, LI H Q. An SPH model for free surface flows with moving rigid objects[J]. International Journal for Numerical Methods in Fluids, 2014, 74(9): 684-697. DOI:10.1002/fld.3868 |
| [35] |
许晓阳, 周亚丽, 余鹏. eXtended Pom-Pom黏弹性流体的改进光滑粒子动力学模拟[J]. 物理学报, 2023, 72(3): 034701. XU X Y, ZHOU Y L, YU P. Improved smoothed particle dynamics simulation of eXtended Pom-Pom viscoelastic fluid[J]. Acta Physica Sinica, 2023, 72(3): 034701. (in Chinese) |
| [36] |
LASO M, ÖTTINGER H C. Calculation of viscoelastic flow using molecular models: The CONNFFESSIT approach[J]. Journal of Non-Newtonian Fluid Mechanics, 1993, 47: 1-20. DOI:10.1016/0377-0257(93)80042-A |