2. 清华大学 航天航空学院, 北京 100084
2. School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
上层大气层飞行器一般指在100~200 km高空长期在轨运行的飞行器[1-2]。相对于现有的低轨卫星,上层大气层飞行器具有诸多优势,最重要的优点就是飞行高度的降低能显著提高地面观测和军事侦察的空间分辨率[3-4]。此外,飞行高度的降低还能有效降低发射成本、减小通信损失、带来更加安全的运行环境,因为轨道高度的降低能减小与空间碎片碰撞的风险和宇宙射线的辐射强度[5]。
但是,上层大气层飞行器的研制面临很多技术挑战。比如,上层大气层驻留的稀薄大气会产生阻力,导致飞行器轨道衰减,降低飞行器寿命[6]。因此,需要提供一套有效的推进系统来抵消稀薄大气阻力。电推进技术虽然比冲高,却需要携带大量的推进剂,导致飞行器质量剧烈增加,难以应用于上层大气层飞行器的阻力补偿[7]。吸气式电推进技术收集并压缩上层大气,利用太阳能将其电离成离子,然后加速排出产生推力[8]。相对于常规的电推进技术,吸气式电推进技术直接使用上层大气作为推进剂,就地取材、变废为宝,不需要额外携带推进剂,能大幅度降低飞行器质量[9],是上层大气层飞行器克服大气阻力的理想推进系统。
吸气式电推进系统由气体收集增压进气道和电推进器构成,前者实现上层大气的收集和压缩,后者负责电离、加速和排出气体产生推力[10]。进气道直接为电离推进器提供推进剂,从上游决定了推进系统的整体性能[11]。Singh等[12]对吸气式电推进系统作了全面的综述,把吸气式电推进系统的研究分为两个时期:冷战时期和当代。冷战时期吸气式电推进系统的研制是为了降低登月任务的推进成本,系统通常都庞大而复杂,一般利用核能作为能源[13-14]。当代的吸气式电推进系统大多是为了抵消超低轨飞行器的阻力,体积较小,使用太阳能作为能源[15]。目前,国内外学者在气体收集增压进气道设计方面都做了大量的工作,文[16-17]综述了相关研究成果。
2003年,日本宇航探索局(Japan Aerospace Exploration Agency, JAXA) 的Nishiyama[8]首次提出吸气式等离子体发动机(air-breathing ion engine, ABIE) 的概念,用于超低轨航天器大气阻力补偿。他还完成了吸气式等离子体发动机的概念设计,包含进气道和电子回旋共振等离子体发动机两部分,前者由准直器和反射器组成。此后,JAXA的Tagawa等[18]对该等离子体发动机进行了实验测试,采用激光爆振束来模拟140~200 km高度的N2组分,结果表明准直器有助于维持N2的压力。Jackson和Marshall[15]也设计了一套吸气式电推进系统,目的是抵消运行在120~300 km高度的上层大气观测卫星CubeSats受到的大气阻力。他们主要关注进气道的收集效率和电推进器的电离效率。欧洲学者在吸气式电推进系统进气道的设计和研究方面也做了一系列工作,比如,Romano等[19-20]为现有的射频等离子体推进器设计了进气道,考虑了气固相互作用(gas-surface interaction, GSI) 为完全漫反射和纯镜面反射两种极端情形;SITAEL公司的Andreussi等[21]基于圆柱和圆锥的初始几何外形,以气体收集效率和压缩因子作为目标函数,对进气道外形进行了单目标和多目标优化,优化后的收集效率不小于25%,压缩因子不低于100。
国内的研究机构几乎与国外同步开展了吸气式电推进系统进气道设计方面的工作。比如,兰州空间物理所的Li等[22]设计了直径为0.5 m的进气道,利用涡轮实现主动增压,气体收集效率达到了57%,涡轮增压显著提高了压缩因子。此外,国防科技大学的吴建军团队[23-24]设计了由捕获段、网格式管道和圆形管道构成的进气道,并评估了其性能,结果表明抛物型捕获段、蜂窝状网格管道和一定长度的圆形管道的组合可获得较好的性能。中国航天空气动力技术研究院的靳旭红等[25]对比了简单斜面型、传统外凹型和内凹型进气道的性能,发现内凹型进气道的收集和压缩性能最好。他们还研究不同飞行高度下进气道的性能[26],发现飞行高度的升高会削弱进气道的压缩和收集性能。
总结现有文献中的吸气式电推进系统进气道设计工作可以发现,进气道设计虽然多种多样,但是GSI模型均为完全漫反射或纯镜面反射。上层大气层GSI的真实物理和化学过程非常复杂,包括吸附、在壁面迁移、解吸附过程,还包括入射气体分子与吸附在壁面上气体分子的碰撞过程,以及原子氧对壁面的侵蚀过程[27],远非简单的漫反射或镜面反射模型所能刻画[28]。近年来,虽然分子动力学手段被广泛用于GSI模拟,但是分子动力学模拟的时间和空间尺度十分有限,因此仍然不存在准确描述上层大气层GSI的模型[29]。在这种情况下,研究GSI模型对进气道收集和压缩性能的影响尤其具有指导意义。
因此,本文采用直接模拟Monte Carlo (direct simulation Monte Carlo, DSMC) 方法对吸气式电推进系统的进气道内流问题进行系统的数值模拟,考虑GSI模型对进气道内流特征的影响,探索进气道压缩和收集性能随着GSI模型参数的变化规律,并从气体动理论的角度阐明其作用机理,为吸气式电推进系统的进气道设计提供参考。
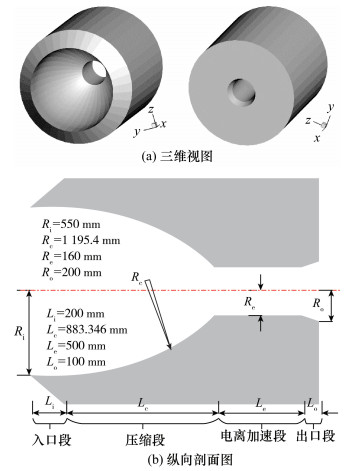
1 流动问题吸气式电推进系统的进气道一般由入口段、压缩段、电离加速段和出口段构成,如图 1所示。高速上层大气通过入口段进入进气道并在压缩段被压缩,之后进入电离加速段被电离成离子并实现加速,最后通过出口段排出。本文的目标是评估进气道的压缩和收集性能,故而仅仅关注中性气体的流动,因为中性气体的流动直接影响推进剂的电离效率[30]。
|
| 图 1 进气道几何外形 |
1.1 进气道外形
本文研究的吸气式电推进系统进气道如图 1所示。考虑到内凹型压缩段能获得较好的气体收集和压缩性能[25],因此该进气道压缩段的轮廓线是内凹的圆弧,这与航空领域传统的外凹型有所不同。
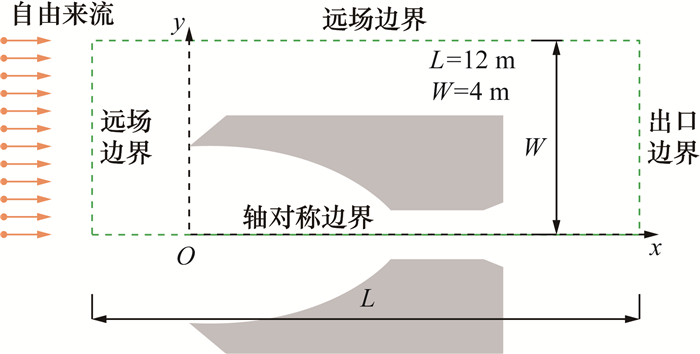
1.2 边界条件图 2是坐标系、计算域和边界条件示意图。坐标原点位于进气道入口段前端面的中心,x轴平行于进气道对称轴,沿流向为正,y轴为径向。计算域轴向和径向尺寸分别为12 m和4 m,超过进气道尺寸的7倍,可以认为足够大。计算域的左端和上端均为远场边界,仿真分子可以自由进出,右端为出口边界,下端为轴对称边界。来流气体为180 km高空的上层大气,速度为7 760 m/s,接近亚轨道速度,进气道表面温度为300 K。根据“美国标准大气(1976)”,来流气体组分、数密度n∞和温度T∞列于表 1中。
|
| 图 2 计算域和边界条件示意图 |
考虑到Maxwell模型在稀薄流模拟中应用最广泛,且具有简洁的形式和满足互易性原理[28],本文采用Maxwell模型来模拟上层大气与进气道表面之间的相互作用。Maxwell模型为漫反射和镜面反射的加权平均,即σ部分的入射分子发生漫反射,剩下的1-σ部分发生镜面反射,其中σ为Maxwell适应系数[29]。本文考虑4个适应系数,即σ=1.0、0.8、0.5和0.2,通过改变Maxwell适应系数σ,采用参数化研究来评估GSI模型对进气道内流特征和进气道性能的影响。
2 计算方法及验证确认 2.1 计算方法稀薄气体流动模拟使用最广泛的方法是Bird[31]提出的DSMC方法。DSMC方法中的分子混沌和稀疏气体假设(即气体分子之间的距离远大于其直径)实现了气体分子运动和碰撞的解耦。分子每运动一个时间步长之后再进行碰撞,分子运动的模拟采用确定论的方法,分子碰撞的模拟则采用概率论的方法[32]。DSMC方法通过仿真分子来实现气体流动的计算,每一个仿真分子代表大量真实气体分子,具有位置、速度和内能等属性。随着模拟过程的进行,通过跟踪仿真分子的轨迹、计算仿真分子之间的碰撞以及仿真分子和固体表面之间的相互作用,实现仿真分子信息的不断更新[33]。计算足够多的时间步以保证流场收敛之后,统计出速度、温度、压力等流场宏观量和表面压力、热流等气动表面量[32]。
基于DSMC方法,本文作者所在的课题组开发了一套通用的三维并行稀薄气体流动分析软件,其核心求解模块为基于自适应非结构/直角网格的DSMC程序[34]。该软件已成功应用于中国的大量航天器中,包括探月工程三期返回舱、火星着陆巡视器和小行星探测器返回舱等。在该DSMC软件中,气体分子模型为变径硬球(variable hard sphere, VHS) 模型[32],气体分子之间的碰撞采用非时间计数(no time counter, NTC) 技术[32]进行模拟,气体分子之间的内能交换模型为Larsen-Borgnakke模型[35]。
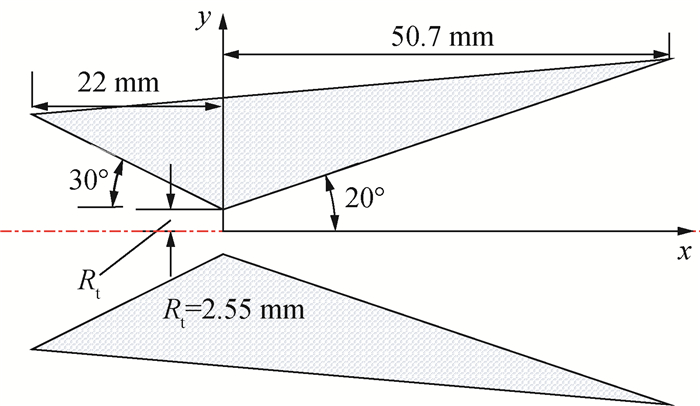
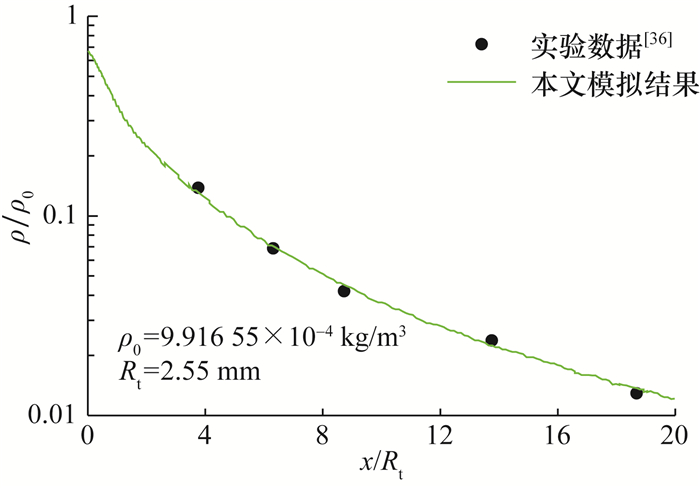
2.2 方法验证验证算例为Rothe低推力喷管内流动问题[36],其几何外形和尺寸如图 3[36]所示。Rothe喷管包括亚声速收缩段和超声速扩张段,收缩段半锥角为30°,扩张段半锥角为20°,喉部半径Rt=2.55 mm。实验气体为纯N2,总压p0=88 Pa,总温T0=300 K。喷管表面为漫反射等温表面,温度与气体总温相等。选择该喷管作为验证算例的原因如下:1) Rothe喷管存在详细的流场密度实验数据[36],是低Reynolds数流动的经典验证算例;2) 该问题是典型的低密度管道内流问题,与本文的进气道内流相似,作为验证算例更有说服力。
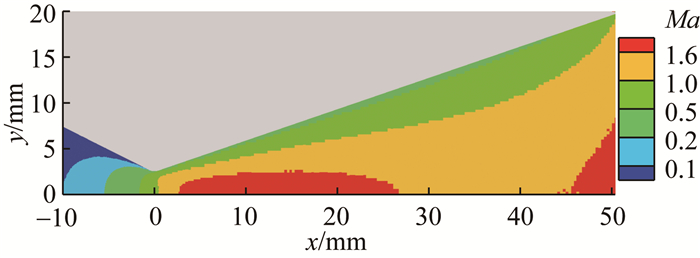
图 4是喷管内部Mach数等值线,表明本文的DSMC方法能准确捕捉喷管内部边界层的亚声速区域,以及在喷管出口后缘终止的声速线。图 5是气体质量密度沿着喷管对称轴的分布,本文的模拟结果与Rothe的实验数据[36]一致,定量验证了本文所采用DSMC方法的可靠性和准确性。
|
| 图 4 喷管流场Mach数等值线 |
|
| 图 5 密度沿着喷管对称轴的分布 |
2.3 方法确认
准确的DSMC模拟要求网格尺寸不能大于当地分子平均自由程,时间步长不能大于当地分子平均碰撞时间[32]。此外,还需要确认每个网格单元的仿真分子数足够多,流场采样之前和采样期间的时间步长数量足够大。因此,设计了3个算例(V1、V2和V3)对网格单元数量Nc、时间步长大小Δt、每个网格单元内的仿真分子数Npc、采样之前的时间步长数量Ntb和采样期间的时间步长数量Nts进行确认。所有确认算例的GSI模型均为漫反射,具体的计算参数列于表 2中。
| 算例 | Nc | Δt/s | Npc | Ntb | Nts |
| V1 | 16 275 | 1.5×10-6 | 100 | 120 000 | 60 000 |
| V2 | 28 006 | 1.0×10-6 | 50 | 100 000 | 40 000 |
| V3 | 28 006 | 1.0×10-6 | 100 | 120 000 | 60 000 |
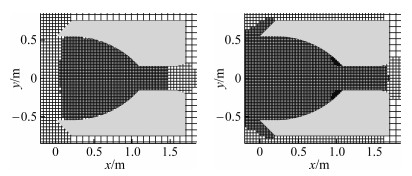
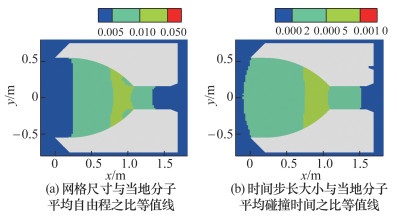
图 6是算例V1和V3的网格示意图。2套网格都在进气道的压缩段和电离加速段实现了自适应加密。图 7a是算例V3中网格尺寸与当地分子平均自由程之比等值线,图 7b是时间步长大小与当地分子平均碰撞时间之比等值线。显然,网格尺寸不到分子平均自由程的1/20,满足DSMC模拟中分子碰撞对的选择要求;时间步长比分子平均碰撞时间低3个量级,满足DSMC模拟中分子运动和碰撞解耦的要求。
|
| 图 6 算例V1和V3的计算网格 |
|
| 图 7 算例V3中网格尺寸与分子平均自由程之比等值线和时间步长与分子平均碰撞时间之比等值线 |
为了对计算结果进行定量确认,令表面压力和剪切应力分别为p和τ,表面压力系数和表面摩擦力系数的定义为
| $ \begin{aligned} & C_p=\left(p-p_{\infty}\right) /\left(0.5 \rho_{\infty} u_{\infty}^2\right), \\ & C_f=\tau /\left(0.5 \rho_{\infty} u_{\infty}^2\right) . \end{aligned} $ | (1) |
式中:p∞为来流压力,ρ∞为来流质量密度,u∞为来流速度。
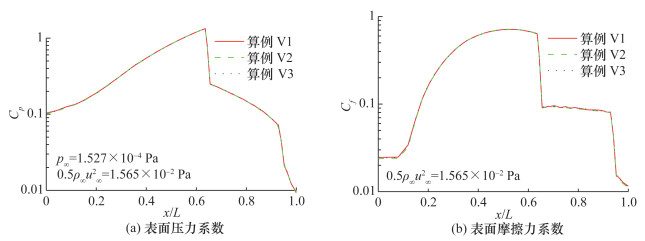
图 8是进气道表面压力系数和表面摩擦力系数分布,采用进气道长度对横坐标进行了量纲归一化。无论是表面压力系数还是表面摩擦力系数,3个算例得出的结果均没有差异,定量确认了计算结果对于网格单元尺寸、时间步长大小、仿真分子数和采样时间步数的无关性,故后续的计算均采用算例V3的参数。
|
| 图 8 确认算例的进气道表面特性分布 |
3 结果和讨论 3.1 流场压力等值线
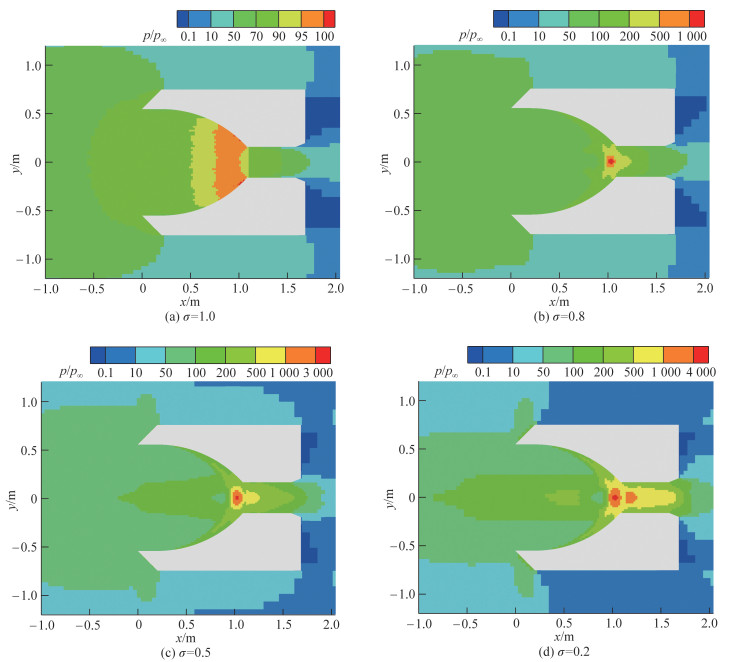
表征进气道压缩性能的参数是压缩因子,即当地压力与来流压力之比。图 9给出了压缩因子等值线,考虑了σ=1.0、0.8、0.5和0.2这4个GSI适应系数。
|
| 图 9 压缩因子p/p∞等值线 |
对于完全漫反射(σ=1.0)的情况,高速、低密度的上层大气进入进气道之后实现了一定程度的压缩,压缩段右部一大片区域的压缩因子最大,接近100,电离加速段左部区域的压缩因子也在70以上。当适应系数降低到0.8时,即80%的气体分子在进气道表面发生漫反射、另外20%发生镜面反射,压缩因子分布发生了明显的变化。在内凹型压缩段发生镜面反射的气体分子汇聚进入电离加速段,压缩因子峰值超过了1 000,且分布在极小的区域内。此时,电离加速段左部区域的压缩因子超过了100。
当适应系数进一步继续降低到0.5时,即一半气体分子发生漫反射、另外一半发生镜面反射,增强的镜面反射汇聚作用使得压缩因子峰值超过了3 000,电离加速段大部分区域的压缩因子也超过了200。当适应系数继续降低到0.2时,即镜面反射的比例升高到80%,汇聚作用进一步增强,压缩因子峰值增大到4 000以上,电离加速段大部分区域的压缩因子也超过了500。此外,对于适应系数σ=0.8、0.5和0.2的情况,适应系数峰值都仅仅分布在极小区域,且中心位置均相同,坐标为(1.029 8 m, 0 m),说明该中心位置就是内凹型压缩段的焦点。
对比上述4个适应系数对应的压缩因子分布,容易发现适应系数的降低能明显提升进气道的压缩性能,不但提高了压缩因子峰值,还增大了整个电离加速段的压缩因子。在内凹型压缩段发生镜面反射的气体分子都汇聚到焦点位置,这正是适应系数的降低能提升进气道压缩性能的机理。适应系数的降低不但增大了进气道的压缩因子,还使得高压区域向右移动,即从压缩段向电离加速段移动,更加有利于被压缩的中性气体在电离加速段实现高效电离。
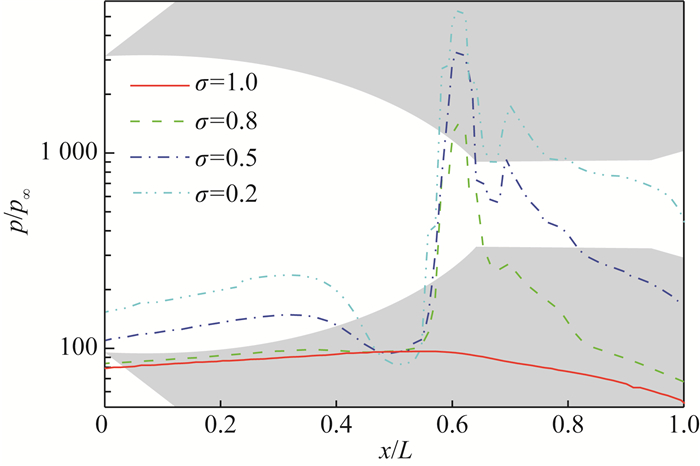
3.2 对称轴压力分布对气体压力进行定量分析,图 10进一步给出了压缩因子沿着进气道对称轴的分布,采用进气道长度对横坐标进行了量纲归一化处理。为了更加清晰地展现进气道压力分布,图 10中还叠加了进气道几何轮廓图。
|
| 图 10 进气道对称轴压力分布 |
观察图 10可以发现,随着GSI适应系数的降低,即镜面反射占比的增加,电离加速段的压缩因子和压缩因子峰值均明显增大。该变化规律与图 9中的压缩因子等值线一致。此外,对于GSI中存在镜面反射的情形(σ=0.8、0.5和0.2),压缩因子存在2个局部峰值:第1个峰值位于内凹压缩段的焦点x=1.029 8 m (即x/L=0.612),前面已经提到过;第2个局部峰值位于x=1.168 9 m (即x/L=0.694)。气体分子通过焦点(第1压力峰值点)之后继续运动,直至与电离加速段壁面碰撞,部分速度矢量相近的气体分子发生镜面反射后再次汇聚到达第2峰值点。
从进气道的压缩性能而言,GSI为完全漫反射时,压缩因子较小,不超过100,且压缩因子较大区域位于压缩段,而不是电离加速段。因此,当进气道表面GSI十分接近漫反射时,应特别留意进气道的压缩性能,因为电离加速段气体压力绝对值太低会导致中性气体的电离效率很低,甚至无法启动[7]。此时,可以考虑把中性气体的电离过程放在压缩段尾部进行,以充分利用该位置较高的压缩因子。
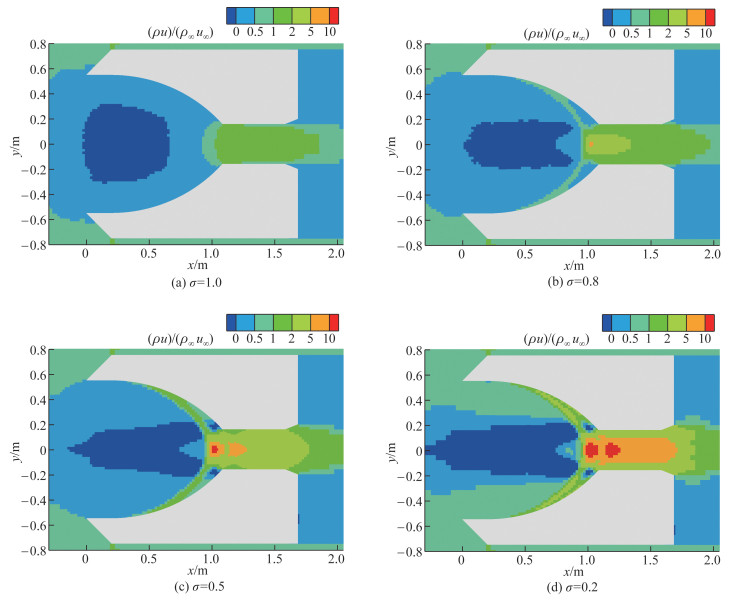
3.3 质量通量等值线表征进气道收集性能的参数是质量通量(单位时间通过单位面积的气体质量),即气体质量密度与流向速度的乘积。图 11给出了量纲为1的质量通量(当地质量通量与来流质量通量之比) 的等值线。
|
| 图 11 量纲为1的质量通量(ρu)/(ρ∞u∞)等值线 |
显然,随着GSI适应系数的降低,通过进气道电离加速段的量纲为1的质量通量明显增大,质量通量峰值也有所增大:GSI为完全漫反射(σ=1.0)时,电离加速段的质量通量低于来流的2倍;GSI中镜面反射的比例变成20%(σ=0.8)时,电离加速段入口中心区域的质量通量增大到来流的2倍以上;GSI中镜面反射比例提高至一半(σ=0.5)时,整个电离加速段的质量通量均大于来流的2倍;GSI中镜面反射比例继续提高至80%(σ=0.2)时,电离加速段大部分区域的质量通量进一步增大到来流的5倍以上。
GSI适应系数的降低,即镜面反射比例的升高,能增大进气道气体质量通量的机制就是内凹型压缩段对发生镜面反射气体分子的汇聚作用。具体而言,由于极低的气体密度和极高的来流速度,进入进气道的气体分子几乎都在做平行于对称轴的自由分子运动,在内凹型压缩段壁面发生镜面反射之后通过焦点进入电离加速段。正是由于内凹型压缩段和镜面反射的汇聚作用,质量通量在压缩段末端的焦点处存在峰值;同样,由于气体分子通过焦点之后继续在电离加速段壁面发生镜面反射,再次汇聚产生了第2质量通量峰值点,这个结果与压力分布类似。
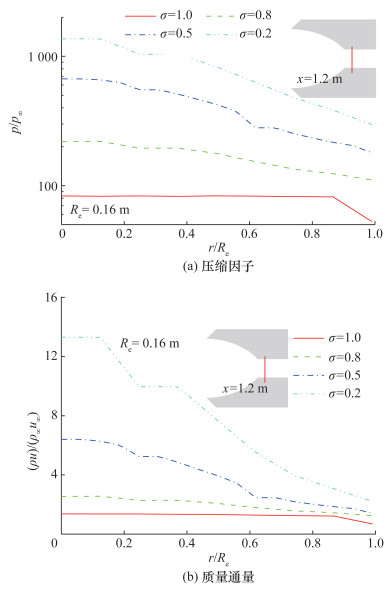
3.4 电离加速段流场剖面压缩后的中性气体主要是在电离加速段电离,因此电离加速段的气体压力和质量通量至关重要。图 12是电离加速段x=1.2 m截面的压缩因子和量纲为1的质量通量剖面图,采用电离加速段半径Re对横坐标进行了量纲归一化处理。为了提升数据可视化效果,图 12中还给出了该截面的示意图。
|
| 图 12 电离加速段x=1.2 m截面流场剖面图 |
显然,随着GSI适应系数的降低,即镜面反射比例的升高,压缩因子和质量通量都明显增大。GSI为完全漫反射(σ=1.0)时,压缩因子低于100,质量通量低于来流的2倍;GSI中镜面反射的比例为80%(σ=0.2)时,压缩因子增大到300左右,质量通量增大到来流的8倍左右。这个结果定量证实了GSI适应系数的降低有助于提升进气道的收集和压缩性能。
3.5 进气道性能评估最后,对进气道的压缩性能和收集性能进行定量评估。表 3列出了σ=1.0、0.8、0.5和0.2这4个GSI适应系数对应的气体压缩因子和收集效率。表 3中的压缩因子为电离加速段x=1.2 m截面的气体平均压力与来流压力的比值,收集效率为通过进气道的气体流率与进入进气道入口的气体流率之比;此外,还列出了其他适应系数对应的压缩因子和收集效率相对于完全漫反射(σ=1.0)工况的变化率。
| σ | 压缩因子 | 收集效率 | |||
| 绝对值 | 变化率/% | 绝对值/% | 变化率/% | ||
| 1.0 | 82.145 | 10.76 | |||
| 0.8 | 156.969 | 91.09 | 15.51 | 44.09 | |
| 0.5 | 336.135 | 309.20 | 25.86 | 140.28 | |
| 0.2 | 683.764 | 732.38 | 52.27 | 385.66 | |
表 3中的数据再次定量证实了GSI适应系数的降低,即GSI中镜面反射比例的升高,有助于提升进气道的收集和压缩性能:GSI为完全漫反射时,压缩因子和收集效率分别只有80和10%左右;适应系数降低到0.8时,压缩因子增大到150,增长率约为90%,收集效率上升到15%,增长率约为44%;适应系数继续降低到0.5时,压缩因子和收集效率分别超过330和25%;适应系数进一步降低到0.2时,压缩因子增大到680以上,增加了7倍多,收集效率超过50%,增长了将近4倍。
上述结果表明,GSI适应系数对进气道的压缩性能和收集性能具有巨大影响,也给吸气式电推进系统进气道的设计提供了新的思路。不同于临近空间超燃冲压发动机进气道单一的几何外形设计,上层大气层吸气式电推进系统的进气道应该采取几何外形/表面材料相互耦合的设计思路。从几何外形的角度,需要采用内凹型压缩段的进气道;从表面材料的角度,需要通过材料选取或表面加工来降低GSI适应系数,使得GSI尽量接近镜面反射。
对于常用的金属回转体内表面,采用从μm到nm尺度的分级抛光加工方法能大幅度降低表面粗糙度,从而降低GSI适应系数。具体的加工方案为:首先采用超精密车削、超精密磨削进行表面μm级加工,然后采用激光抛光技术进行表面nm级加工,最后采用氩离子抛光、单点金刚石车削技术进行超精密抛光。然而,上层大气包含大量的原子氧,会严重侵蚀进气道表面,导致其表面粗糙度增加,从而降低性能[37]。目前常用的原子氧防护方法有两种:采用抗原子氧侵蚀材料和增加抗原子氧防护涂层。前者主要有金属铝、氧化铝、有机硅、癸硼烷基聚合物、硼-硅聚合物、含氟聚合物以及含磷聚合物等材料,后者主要包括含有有机硅的防护涂层和含有无机氧化物的防护涂层[38]。无论是抗原子氧侵蚀材料还是抗原子氧防护涂层,都能显著提升进气道表面的抗原子氧侵蚀能力[39],从而保证进气道的压缩和收集性能。
4 结论采用DSMC方法对吸气式电推进系统的进气道内流问题进行了系统的数值模拟,考虑GSI模型对进气道内流特征的影响,探索进气道压缩和收集性能随着GSI适应系数的变化规律,并从气体动理论的角度阐明其作用机理,得到结论如下:
1) GSI模型对进气道的压缩性能具有巨大的影响,适应系数的降低,即GSI中镜面反射比例的升高,不但能显著提高压缩因子,适应系数从1.0降低到0.2导致压缩因子增大7倍多,还使得高压区域向右移动至电离加速段,有利于中性气体的高效电离。
2) GSI模型显著影响进气道的收集性能,适应系数的降低能明显提高进气道的气体质量通量和收集效率,适应系数从1.0降低到0.2导致收集效率增大将近4倍。
3) GSI适应系数的降低,即GSI中镜面反射比例的升高,增大进气道压力和质量通量的机制是气体分子在内凹型压缩段壁面发生镜面反射之后汇聚通过焦点,并进入电离加速段。
4) 上层大气层吸气式电推进系统的进气道应该采取几何外形/表面材料相互耦合的设计思路,不仅采用内凹型压缩段的进气道,还需要通过材料选取或表面加工降低GSI适应系数,使得GSI尽量接近镜面反射。
| [1] |
沈清, 黄飞, 程晓丽, 等. 飞行器上层大气层空气动力特性探讨[J]. 气体物理, 2021, 6(1): 1-9. SHEN Q, HUANG F, CHENG X L, et al. On characteristics of upper atmosphere aerodynamics of flying vehicles[J]. Physics of Gases, 2021, 6(1): 1-9. (in Chinese) |
| [2] |
CHEN Z, HUANG F, JIN X H, et al. A novel lightweight aerodynamic design for the wings of hypersonic vehicles cruising in the upper atmosphere[J]. Aerospace Science and Technology, 2021, 109: 106418. DOI:10.1016/j.ast.2020.106418 |
| [3] |
CRISP N H, ROBERTS P C E, LIVADIOTTI S, et al. The benefits of very low earth orbit for earth observation missions[J]. Progress in Aerospace Sciences, 2020, 117: 100619. DOI:10.1016/j.paerosci.2020.100619 |
| [4] |
靳旭红, 黄飞, 程晓丽, 等. 超低地球轨道卫星大气阻力预测与影响因素分析[J]. 清华大学学报(自然科学版), 2020, 60(3): 219-226. JIN X H, HUANG F, CHENG X L, et al. Atmospheric drag on satellites flying in lower low-earth orbit[J]. Journal of Tsinghua University (Science & Technology), 2020, 60(3): 219-226. (in Chinese) |
| [5] |
CRISP N H, ROBERTS P C E, LIVADIOTTI S, et al. In-orbit aerodynamic coefficient measurements using SOAR (satellite for orbital aerodynamics research)[J]. Acta Astronautica, 2021, 180: 85-99. DOI:10.1016/j.actaastro.2020.12.024 |
| [6] |
PRIETO D M, GRAZIANO B P, ROBERTS P C E. Spacecraft drag modelling[J]. Progress in Aerospace Sciences, 2014, 64: 56-65. DOI:10.1016/j.paerosci.2013.09.001 |
| [7] |
GARRIGUES L. Computational study of Hall-effect thruster with ambient atmospheric gas as propellant[J]. Journal of Propulsion and Power, 2012, 28(2): 344-354. DOI:10.2514/1.B34307 |
| [8] |
NISHIYAMA K. Air breathing ion engine concept[C]//Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation. Bremen, Germany: AIAA, 2003: 1-8.
|
| [9] |
PEKKER L, KEIDAR M. Analysis of airbreathing Hall-effect thrusters[J]. Journal of Propulsion and Power, 2012, 28(6): 1399-1405. DOI:10.2514/1.B34441 |
| [10] |
靳旭红, 程晓丽, 沈清, 等. 吸气式电推进系统进气道气体流动数值分析[J]. 中国科学: 物理学力学天文学, 2024, 54(3): 234712. JIN X H, CHENG X L, SHEN Q, et al. Numerical analysis of inlet flows in an atmosphere-breathing electric propulsion system[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2024, 54(3): 234712. (in Chinese) |
| [11] |
ROMANO F, CHAN Y A, HERDRICH G, et al. RF helicon-based inductive plasma thruster (IPT) design for an atmosphere-breathing electric propulsion system (ABEP)[J]. Acta Astronautica, 2020, 176: 476-483. DOI:10.1016/j.actaastro.2020.07.008 |
| [12] |
SINGH L A, WALKER M L R. A review of research in low earth orbit propellant collection[J]. Progress in Aerospace Sciences, 2015, 75: 15-25. DOI:10.1016/j.paerosci.2015.03.001 |
| [13] |
BERNER F, CAMAC M. Air scooping vehicle[J]. Planetary and Space Science, 1961, 4: 159-183. DOI:10.1016/0032-0633(61)90130-1 |
| [14] |
DEMETRIADES S T. A novel system for space flight using a propulsive fluid accumulator[J]. Journal of the British Interplanetary Society, 1959, 17: 114-119. |
| [15] |
JACKSON S W, MARSHALL R. Conceptual design of an air-breathing electric thruster for CubeSat applications[J]. Journal of Spacecraft and Rockets, 2018, 55(3): 632-639. DOI:10.2514/1.A33993 |
| [16] |
WU J J, ZHENG P, ZHANG Y, et al. Recent development of intake devices for atmosphere-breathing electric propulsion system[J]. Progress in Aerospace Sciences, 2022, 133: 100848. DOI:10.1016/j.paerosci.2022.100848 |
| [17] |
ANDREUSSI T, FERRATO E, GIANNETTI V. A review of air-breathing electric propulsion: From mission studies to technology verification[J]. Journal of Electric Propulsion, 2022, 1(1): 31. DOI:10.1007/s44205-022-00024-9 |
| [18] |
TAGAWA M, YOKOTA K, NISHIYAMA K, et al. Experimental study of air breathing ion engine using laser detonation beam source[J]. Journal of Propulsion and Power, 2013, 29(3): 501-506. DOI:10.2514/1.B34530 |
| [19] |
ROMANO F, MASSUTI-BALLESTER B, BINDER T, et al. System analysis and test-bed for an atmosphere-breathing electric propulsion system using an inductive plasma thruster[J]. Acta Astronautica, 2018, 147: 114-126. DOI:10.1016/j.actaastro.2018.03.031 |
| [20] |
ROMANO F, ESPINOSA-OROZCO J, PFEIFFER M, et al. Intake design for an atmosphere-breathing electric propulsion system (ABEP)[J]. Acta Astronautica, 2021, 187: 225-235. DOI:10.1016/j.actaastro.2021.06.033 |
| [21] |
ANDREUSSI T, FERRATO E, PAISSONI C A, et al. The AETHER project: Development of air-breathing electric propulsion for VLEO missions[J]. CEAS Space Journal, 2022, 14(4): 717-740. DOI:10.1007/s12567-022-00442-3 |
| [22] |
LI Y W, CHEN X, LI D M, et al. Design and analysis of vacuum air-intake device used in air-breathing electric propulsion[J]. Vacuum, 2015, 120: 89-95. DOI:10.3969/j.issn.1002-8935.2015.02.018 |
| [23] |
ZHENG P, WU J J, WU B Q, et al. Design and numerical investigation on the intake of atmosphere-breathing electric propulsion[J]. Acta Astronautica, 2021, 188: 215-228. DOI:10.1016/j.actaastro.2021.07.036 |
| [24] |
ZHENG P, WU J J, ZHANG Y, et al. Design and optimization of vacuum intake for atmosphere-breathing electric propulsion (ABEP) system[J]. Vacuum, 2022, 195: 110652. DOI:10.1016/j.vacuum.2021.110652 |
| [25] |
JIN X H, MIAO W B, CHENG X L, et al. Monte Carlo simulation of inlet flows in atmosphere-breathing electric propulsion[J]. AIAA Journal, 2024, 62(2): 518-529. DOI:10.2514/1.J062718 |
| [26] |
JIN X H, CHENG X L, HUANG Y Q, et al. Numerical analysis of inlet flows at different altitudes in the upper atmosphere[J]. Physics of Fluids, 2023, 35(9): 093605. DOI:10.1063/5.0160002 |
| [27] |
LIANG Z, KEBLINSKI P. Parametric studies of the thermal and momentum accommodation of monoatomic and diatomic gases on solid surfaces[J]. International Journal of Heat and Mass Transfer, 2014, 78: 161-169. DOI:10.1016/j.ijheatmasstransfer.2014.06.038 |
| [28] |
靳旭红, 黄飞, 程晓丽, 等. Maxwell气固相互作用模型对稀薄高超声速凹腔绕流流动特征和热环境的影响[J]. 航空学报, 2021, 42(3): 124118. JIN X H, HUANG F, CHENG X L, et al. Effect of Maxwell gas-surface interaction models on flow characteristics and thermodynamic properties of rarefied hypersonic cavity flows[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(3): 124118. (in Chinese) |
| [29] |
LIVADIONTTI S, CRISP N H, ROBERTS P C E, et al. A review of gas-surface interaction models for orbital aerodynamics applications[J]. Progress in Aerospace Sciences, 2020, 119: 100675. DOI:10.1016/j.paerosci.2020.100675 |
| [30] |
BOYD I D, VAN GILDER D B, LIU X M. Monte Carlo simulation of neutral xenon flows in electric propulsion devices[J]. Journal of Propulsion and Power, 1998, 14(6): 1009-1015. DOI:10.2514/2.5366 |
| [31] |
BIRD G A. Approach to translational equilibrium in a rigid sphere gas[J]. Physics of Fluids, 1963, 6(10): 1518-1519. DOI:10.1063/1.1710976 |
| [32] |
BIRD G A. Molecular gas dynamics and the direct simulation of gas flows[M]. New York, USA: Oxford University Press, 1994: 340-346.
|
| [33] |
BIRD G A. Monte Carlo simulation of gas flows[J]. Annual Review of Fluid Mechanics, 1978, 10: 11-31. DOI:10.1146/annurev.fl.10.010178.000303 |
| [34] |
靳旭红, 黄飞, 程晓丽, 等. 稀薄流区高超声速飞行器表面缝隙流动结构及气动热环境的分子模拟[J]. 航空动力学报, 2019, 34(1): 201-209. JIN X H, HUANG F, CHENG X L, et al. Monte Carlo simulation for the flow-field structure and aerodynamic heating due to cavities on hypersonic vehicle surfaces in the rarefied flow regime[J]. Journal of Aerospace Power, 2019, 34(1): 201-209. (in Chinese) |
| [35] |
BORGNAKKE C, LARSEN P S. Statistical collision model for Monte Carlo simulation of polyatomic gas mixture[J]. Journal of Computational Physics, 1975, 18(4): 405-420. DOI:10.1016/0021-9991(75)90094-7 |
| [36] |
ROTHE D E. Electron-beam studies of viscous flow in supersonic nozzles[J]. AIAA Journal, 1971, 9(5): 804-811. DOI:10.2514/3.6279 |
| [37] |
贺金梅, 赵丹, 郑楠, 等. 航天材料的抗原子氧防护技术研究进展[J]. 现代化工, 2013, 33(8): 21-24, 26. HE J M, ZHAO D, ZHENG N, et al. Protection technology research progress of resistance to atomic oxygen on space materials[J]. Modern Chemical Industry, 2013, 33(8): 21-24, 26. DOI:10.3969/j.issn.0253-4320.2013.08.006 (in Chinese) |
| [38] |
李昊耕, 谷红宇, 章俞之, 等. 聚合物材料表面原子氧防护技术的研究进展[J]. 无机材料学报, 2019, 34(7): 685-693. LI H G, GU H Y, ZHANG Y Z, et al. Surface protection of polymer materials from atomic oxygen: A review[J]. Journal of Inorganic Materials, 2019, 34(7): 685-693. (in Chinese) |
| [39] |
袁璐, 许旻, 李毅, 等. 聚酰亚胺材料的抗原子氧防护技术研究进展[J/OL]. 材料导报, 2023: 1-17. (2023-12-21)[2024-02-02]. https://link.cnki.net/urlid/50.1078.TB.20231220.1641.008 YUAN L, XU M, LI Y, et al. Advanced progress of atomic oxygen resistant techniques on polyimide materials[J/OL]. Materials Reports, 2023: 1-17. (2023-12-21)[2024-02-02]. https://link.cnki.net/urlid/50.1078.TB.20231220.1641.008. (in Chinese) |