随着现代飞行器设计对机动性要求的提高，飞行器常常要经历大攻角与大舵偏角的飞行工况^[1]。例如，新一代空空导弹由于采用了升力面非常有限的气动布局，使增大攻角提高升力成为增强导弹机动能力的主要途径^[2]。飞行力学常用坐标系间的转换关系中含有包括攻角在内的8个角度，动力学方程中各个运动变量和作用力向不同坐标系的投影和坐标转换，使飞行动力学模型通常是复杂的非线性方程，因此在进行轨迹优化和飞行控制系统设计时要对其进行线性化处理。目前，国内外学者已在小扰动线性化^[3]、线性变参数模型^[4-6]以及反馈线性化^[7-10]等非线性模型线性化的方法和应用方面进行了较多研究。Hesse等^[11]研究了细长柔性翼飞行器非线性飞行动力学响应中结构变形的线性化，建立了完整保留刚性和弹性运动之间耦合的模型。李锋等^[12]采用小扰动法建立了考虑风场影响的临近空间太阳能飞行器线性化横航向动力学模型，解决了大多利用非线性模型研究风场影响的传统方法无法用于分析飞行器本体稳定性的问题。杜万闪等^[13]提出了反映相对滚转运动的8自由度组合式三体飞行器动力学模型，并采用小扰动法推导其状态空间形式的线性化动力学方程，进而分析了飞行器在不同配平状态的飞行动力学特性。仇靖雯等^[14]在对飞行器参考轨迹进行优化设计的基础上，将飞行器的非线性动力学模型沿参考轨迹进行线性化，建立了四翼变掠角飞行器的线性变参数模型。He等^[15]建立了气动弹性与飞行动力学耦合的大柔性飞行器非线性动力学模型，通过在非线性平衡点进行Taylor展开实现模型线性化，进而得到了一系列降阶的线性变参数模型。王乾等^[16]建立了抑制侧滑条件下无人机航迹跟踪侧向运动的非线性模型，再通过反馈线性化转化为带有扰动的线性模型，进一步优化得到了航迹跟踪反馈控制参数。

文[17]中给出了航天工程中常用的飞行器纵向动力学线性化模型。该模型是针对运载火箭建立的，使用了攻角与操纵机构摆动角为小量等假设。对于高超声速飞行器、战术导弹等对机动性要求较高的飞行器，其飞行条件已不满足上述假设，需要建立更加精细的线性化动力学模型。本文在文[18]建立的矢量形式的弹性飞行器飞行动力学模型的基础上，首先通过向指定坐标系投影得到矩阵形式的标量方程，然后采用小扰动法推导其在大攻角与大舵偏角条件下的高精度线性化形式，并与文[17]给出的航天工程中常用模型进行对比分析。

1 飞行器动力学方程的矩阵形式

将文[18]中给出的飞行器刚柔耦合飞行动力学的矢量方程分别向弹道系或本体系投影，得到矩阵形式的标量方程。在本文中，惯性系O_ax_ay_az_a、本体系O₁x₁y₁z₁与舵面系O_px_py_pz_p的定义与文[18]一致，弹道系O₂x₂y₂z₂采用飞行力学的常用定义^[19]。

将飞行器平动动力学方程投影到弹道系得

$ m \dot{\boldsymbol{V}}-\boldsymbol{A}_{21} \widetilde{\boldsymbol{S}} \boldsymbol{\dot{\omega}}_{\mathrm{c}}+\boldsymbol{A}_{21} \boldsymbol{C}_{\mathrm{i}} \ddot{\boldsymbol{q}}_{\mathrm{c}}=\boldsymbol{F}-\boldsymbol{Q}_{\rm t} . $

(1)

式中：A₂₁为本体系向弹道系转换的方向余弦阵；m为飞行器的总质量；S=(S_x S_y S_z)^T为飞行器相对本体系的总静矩在本体系的投影；矩阵上方的波浪号表示将该列阵变换为由其坐标组成的三阶反对称方阵；ω_c为本体系相对惯性系的转动角速度在本体系的投影；C_t为飞行器振动对平动的耦合系数矩阵，具体表达式见文[18]，记其第j(j=1, 2, …, s)列为(C_{tx, j}C_{ty, j}C_{tz, j})^T，s为截取的模态数；q_c=(q_{c, 1} q_{c, 2} … q_{c, s})^T为本体振动的模态坐标列阵；F=(F_x F_y F_z)^T为飞行器主动力的合力在弹道系的投影；Q_t=(Q_tx Q_ty Q_tz)^T为飞行器平动耦合惯性力的合力在弹道系的投影，是飞行器的姿态角速度、舵偏角速度、本体与舵面的静矩等参数的函数；$\dot{\boldsymbol{V}} $为飞行器的速度在惯性系中的绝对导数在弹道系的投影，与在弹道系中的相对导数$\frac{\delta \boldsymbol{V}}{\delta t}$的关系为

$ \dot{\boldsymbol{V}}=\frac{\delta \boldsymbol{V}}{\delta t}+\widetilde{\boldsymbol{\varOmega}} \boldsymbol{V} . $

(2)

式中：V=(V 0 0)^T为飞行器的速度在弹道系的投影；Ω为弹道系相对惯性系的转动角速度在弹道系的投影，

$ \boldsymbol{\varOmega}=\left[\begin{array}{c} -\dot{\theta} \sin \sigma \\ \dot{\sigma} \\ \dot{\theta} \cos \sigma \end{array}\right]. $

(3)

式中：θ为弹道倾角，σ为弹道偏角。将式(3)代入式(2)得

$ \dot{\boldsymbol{V}}=\left[\begin{array}{c} \dot{V} \\ V \dot{\theta} \cos \sigma \\ -V \dot{\sigma} \end{array}\right]. $

(4)

将飞行器姿态动力学方程投影到本体系得

$ \widetilde{\boldsymbol{S}} \boldsymbol{A}_{21}^{\mathrm{T}} \dot{\boldsymbol{V}}+\boldsymbol{J} \boldsymbol{\dot{\omega}}_{\mathrm{c}}+\boldsymbol{C}_{\mathrm{r}} \ddot{\boldsymbol{q}}_{\mathrm{c}}=\boldsymbol{T}-\boldsymbol{Q}_{\mathrm{r}} . $

(5)

式中：J为飞行器相对本体系的总惯量矩阵；C_r为飞行器振动对转动的耦合系数矩阵，具体表达式见文[18]，记其第j(j=1, 2, …, s)列为(C_{rx, j} C_{ry, j} C_{rz, j})^T；T为飞行器主动力矩的合力矩在本体系的投影；Q_r=(Q_rx Q_ry Q_rz)^T为飞行器转动耦合惯性力的合力在本体系的投影，是飞行器的姿态角速度、舵偏角速度、本体与舵面的转动惯量等参数的函数。

将飞行器振动动力学方程投影到本体系得

$ \boldsymbol{C}_{\mathrm{t}}^{\mathrm{T}} \boldsymbol{A}_{21}^{\mathrm{T}} \dot{\boldsymbol{V}}+\boldsymbol{C}_{\mathrm{r}}^{\mathrm{T}} \boldsymbol{\dot{\omega}}_{\mathrm{c}}+\boldsymbol{M}_{\mathrm{f}} \ddot{\boldsymbol{q}}_{\mathrm{c}}+\boldsymbol{C}_{\mathrm{c}} \dot{\boldsymbol{q}}_{\mathrm{c}}+\boldsymbol{K}_{\mathrm{c}} \boldsymbol{q}_{\mathrm{c}}=\boldsymbol{F}_{\mathrm{f}}-\boldsymbol{Q}_{\mathrm{f}}. $

(6)

式中：M_f为飞行器的模态质量矩阵，具体表达式见文[18]；C_c为飞行器本体的模态阻尼矩阵，K_c为模态刚度矩阵；F_f为飞行器的模态力在本体系的投影；Q_f=(Q_{f, 1} Q_{f, 2} … Q_{f, s})^T为飞行器振动耦合惯性力的合力在本体系的投影，是飞行器的姿态角速度、舵偏角速度、本体的模态矢量与模态坐标的导数等参数的函数。

2 飞行器纵向动力学模型的线性化 2.1 动力学方程的线性化方法

在第1章给出的矩阵形式的动力学方程中，每一个分量方程具有式(7)形式：

$ \sum\limits_{i=1}^{n} g_{i} \frac{\mathrm{d} y_{i}}{\mathrm{~d} t}=Q . $

(7)

式中：g_i(i=1, 2, …, n)和Q是状态变量y_i(i=1, 2, …, n)的函数。设未扰动运动中的状态变量为y_i=y_i0(t)，代入式(7)得

$ \sum\limits_{i=1}^{n} g_{i 0} \frac{\mathrm{d} y_{i 0}}{\mathrm{~d} t}=Q_{0} . $

(8)

其中：

$ \begin{aligned} g_{i 0} & =g_{i}\left(y_{10}, y_{20}, \cdots, y_{n 0}\right) ,\\ Q_{0} & =Q\left(y_{10}, y_{20}, \cdots, y_{n 0}\right). \end{aligned} $

将状态变量及其函数表示为未扰动运动中的值与偏量之和，

$ \begin{cases}y_{i}=y_{i 0}+\Delta y_{i} & (i=1, 2, \cdots, n), \\ g_{i}=g_{i 0}+\Delta g_{i} & (i=1, 2, \cdots, n), \\ Q=Q_{0}+\Delta Q.\end{cases} $

(9)

式中：Δg_i和ΔQ分别表示函数g_i和Q在扰动运动和未扰动运动中的差值。将g_i和Q在未扰动运动附近进行Taylor展开并只保留一阶项：

$ \Delta g_{i} =\sum\limits_{j=1}^{n}\left(\frac{\partial g_{i}}{\partial y_{j}}\right)_{0} \Delta y_{j} , $

(10)

$ \Delta Q =\sum\limits_{j=1}^{n}\left(\frac{\partial Q}{\partial y_{j}}\right)_{0} \Delta y_{j} . $

(11)

式中：$\left(\frac{\partial g_{i}}{\partial y_{j}}\right)_{0}(i, j=1, 2, \cdots, n)$和$\left(\frac{\partial Q}{\partial y_{j}}\right)_{0}(j=1, 2, \cdots, n)$分别表示偏导数$\frac{\partial g_{i}}{\partial y_{j}}$和$\frac{\partial Q}{\partial y_{j}}$在未扰动运动中的值。

将式(9)代入式(7)，根据式(8)消去等式中的部分未扰动运动量，并略去高阶小量$\Delta g_{i} \frac{\mathrm{d} \Delta y_{i}}{\mathrm{~d} t}$，得到式(7)的线性化增量形式为

$ \sum\limits_{i=1}^{n} g_{i 0} \frac{\mathrm{d} \Delta y_{i}}{\mathrm{~d} t}=\Delta Q-\sum\limits_{i=1}^{n} \Delta g_{i} \frac{\mathrm{d} y_{i 0}}{\mathrm{~d} t} . $

(12)

2.2 纵向动力学方程的线性化

在纵向动力学模型中，将侧滑角、速度倾斜角、弹道偏角以及飞行器的姿态角速度在本体系x轴和y轴的分量等运动参数视为小量，并忽略二阶及以上的小量。将式(1)的x方向的分量方程代入式(12)，等号右侧只保留主动力和耦合惯性力的偏量，

$ a_{11} \Delta \dot{V}+a_{12} \Delta \dot{\omega}_{\mathrm{c}z}+\sum\limits_{j=1}^{s} a_{13, j} \Delta \ddot{q}_{\mathrm{c}, j}=\Delta F_{x}-\Delta Q_{\mathrm{t} x} . $

(13)

其中：

$ \begin{gathered} a_{11}=m, \\ a_{12}=-\cos \alpha S_{y}-\sin \alpha S_{x}, \\ a_{13, j}=\cos \alpha C_{\mathrm{t} x, j}-\sin \alpha C_{\mathrm{t} y, j}. \end{gathered} $

式中：α为飞行器的攻角；ω_cz为本体系相对惯性系的转动角速度在本体系z轴的分量，在纵向运动中ω_cz=$\dot{\varphi}$，φ为俯仰角。

同样地，将式(1)的y方向的分量方程代入式(12)可得

$ a_{21} \Delta \dot{\theta}+a_{22} \Delta \dot{\omega}_{\mathrm{c}z}+\sum\limits_{j=1}^{s} a_{23, j} \Delta \ddot{q}_{\mathrm{c}, j}=\Delta F_{y}-\Delta Q_{\mathrm{t}y} . $

(14)

其中：

$ \begin{gathered} a_{21}=m V, \\ a_{22}=\cos \alpha S_{x}-\sin \alpha S_{y}, \\ a_{23, j}=\sin \alpha C_{\mathrm{t} x, j}+\cos \alpha C_{\mathrm{t} y, j}. \end{gathered} $

将式(5)的z方向的分量方程代入式(12)可得

$ \begin{gathered} a_{31} \Delta \dot{\omega}_{\mathrm{c}z}+a_{32} \Delta \dot{V}+a_{33} \Delta \dot{\theta}+\sum\limits_{j=1}^{s} a_{34, j} \Delta \ddot{q}_{\mathrm{c}, j}=\\ \Delta T_{z}-\Delta Q_{\mathrm{r} z} . \end{gathered} $

(15)

其中：

$ \begin{gathered} a_{31}=J_{z z}, \\ a_{32}=-\left(\cos \alpha S_{y}+\sin \alpha S_{x}\right), \\ a_{33}=V\left(\cos \alpha S_{x}-\sin \alpha S_{y}\right), \\ a_{34, j}=C_{\mathrm{r} z, j} . \end{gathered} $

式中J_zz为飞行器相对本体系z轴的总转动惯量。

将式(6)的第j(j=1, 2, …, s)个分量方程代入式(12)可得

$ \begin{gather*} \sum\limits_{k=1}^{s} a_{41, j k} \Delta \ddot{q}_{\mathrm{c}, k}+a_{42, j} \Delta \dot{V}+a_{43, j} \Delta \dot{\theta}+a_{44, j} \Delta \dot{\omega}_{\mathrm{c}z}= \\ \Delta F_{\mathrm{f}, j}-\Delta Q_{\mathrm{f}, j}-a_{45, j} \Delta \dot{q}_{\mathrm{c}, j}-a_{46, j} \Delta q_{\mathrm{c}, j} . \end{gather*} $

(16)

其中：

$ \begin{gathered} a_{41, j k}=M_{j k}, \\ a_{42, j}=\cos \alpha C_{\mathrm{t} x, j}-\sin \alpha C_{\mathrm{t} y, j}, \\ a_{43, j}=\left(\sin \alpha C_{\mathrm{t} x, j}+\cos \alpha C_{\mathrm{t} y, j}\right) V, \\ a_{44, j}=C_{\mathrm{r}z, j}, \\ a_{45, j}=C_{j}, \\ a_{46, j}=K_{j} . \end{gathered} $

式中：M_jk为飞行器的模态质量矩阵M_f的第j行第k列元素，C_j为飞行器本体的第j阶模态阻尼，K_j为第j阶模态刚度。

2.3 操纵机构摆动惯性力与力矩的线性化

当飞行器的舵面等操纵机构摆动时，将产生摆动惯性力，构成式(1)、(5)与(6)中耦合惯性力的一部分。设舵面绕本体系的z轴转动，仅考虑由摆动角加速度产生的惯性力与力矩，则舵面摆动惯性力在弹道系的投影P_t、摆动惯性力矩与模态力在本体系的投影P_r与P_f分别为：

$ \begin{gathered} \boldsymbol{P}_{\mathrm{t}}=\sum\limits_{i=1}^{n_{\mathrm{p}}} \boldsymbol{A}_{21}\left[-\widetilde{\left(\boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{S}_{\mathrm{p}, i}\right)}\left(\boldsymbol{A}_{1 \mathrm{p}, i} \dot{\boldsymbol{\omega}}_{\mathrm{p}, i}+\right.\right. \\ \left.\left.\widetilde{\boldsymbol{\omega}}_{\mathrm{c}} \boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{\omega}_{\mathrm{p}, i}\right)\right], \end{gathered} $

(17)

$ \begin{gathered} \boldsymbol{P}_{\mathrm{r}}=\sum\limits_{i=1}^{n_{\mathrm{p}}}\left[-\tilde{\boldsymbol{r}}_{\mathrm{cp}, i} \widetilde{\left(\boldsymbol{A}_{1\mathrm{p}, i} \boldsymbol{S}_{\mathrm{p}, i}\right)}\left(\boldsymbol{A}_{1 \mathrm{p}, i} \dot{\boldsymbol{\omega}}_{\mathrm{p}, i}+\right.\right. \\ \left.\widetilde{\boldsymbol{\omega}}_{\mathrm{c}} \boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{\omega}_{\mathrm{p}, i}\right)+ \\ \left.\boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{J}_{\mathrm{p}, i} \boldsymbol{A}_{1 \mathrm{p}, i}^{\mathrm{T}}\left(\boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{\omega}_{\mathrm{p}, i}+\widetilde{\boldsymbol{\omega}}_{\mathrm{c}} \boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{\omega}_{\mathrm{p}, i}\right)\right], \end{gathered} $

(18)

$ \begin{gathered} \boldsymbol{P}_{\mathrm{f}}=\sum\limits_{i=1}^{n_{\mathrm{p}}} \boldsymbol{\varPhi}_{\mathrm{c}, i}^{\mathrm{r}} \cdot \mathrm{T}\left[-\widetilde{\left(\boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{S}_{\mathrm{p}, i}\right)}\left(\boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{\dot{\omega}}_{\mathrm{p}, i}+\right.\right.\\ \left.\left.\widetilde{\boldsymbol{\omega}}_{\mathrm{c}} \boldsymbol{A}_{1 \mathrm{p}, i} \boldsymbol{\omega}_{\mathrm{p}, i}\right)\right] . \end{gathered} $

(19)

式中：$\boldsymbol{\omega}_{\mathrm{p}, i}=\left(\begin{array}{lll}0 & 0 & \dot{\alpha}_{\mathrm{p}, i}\end{array}\right)^{\mathrm{T}}$为第i个舵面系相对本体系的转动角速度在舵面系的投影，α_{p, i}为第i个舵面的舵偏角；$\boldsymbol{r}_{\mathrm{cp}, i}=\left(r_{\mathrm{cp} x, i} r_{\mathrm{cp} y, i} r_{\mathrm{cp}z, i}\right)^{\mathrm{T}}$为第i个舵面系原点相对本体系原点的矢径在本体系的投影；$\boldsymbol{S}_{\mathrm{p}, i}=\left(S_{\mathrm{p} x, i} S_{\mathrm{p} y, i} S_{\mathrm{p} z, i}\right)^{\mathrm{T}}$为第i个舵面相对舵面系的静矩在舵面系的投影；J_{p, i}为第i个舵面相对舵面系的惯量矩阵；Φ_{c, i}^r为本体上与第i个舵面连接点的模态矩阵，记其第j(j=1, 2, …, s)列为$\left(\varphi_{j x, i}^{\mathrm{r}} \varphi_{j y, i}^{\mathrm{r}} \varphi_{j z, i}^{\mathrm{r}}\right)^{\mathrm{T}}$；$\boldsymbol{A}_{1 \mathrm{p}, i}$为第i个舵面系向本体系转换的方向余弦阵；n_p为舵面的数量。

将摆动惯性力在弹道系x方向的投影P_tx代入式(11)可得

$ \Delta P_{\mathrm{t} x}=\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{11, i} \Delta \ddot{\alpha}_{\mathrm{p}, i}+\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{12, i} \Delta \alpha_{\mathrm{p}, i}+d_{13} \Delta \alpha . $

(20)

其中：

$ \begin{gathered} d_{11, i}=-\left(\cos \alpha \sin \alpha_{\mathrm{p}, i}+\sin \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} x, i}+ \\ \left(\sin \alpha \sin \alpha_{\mathrm{p}, i}-\cos \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} y, i} ,\\ d_{12, i}=\left[\left(\sin \alpha \sin \alpha_{\mathrm{p}, i}-\cos \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} x, i}+\right. \\ \left.\left(\cos \alpha \sin \alpha_{\mathrm{p}, i}+\sin \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} y, i}\right] \ddot{\alpha}_{\mathrm{p}, i} ,\\ d_{13}=\sum\limits_{i=1}^{n_{\mathrm{p}}}\left[\left(\sin \alpha \sin \alpha_{\mathrm{p}, i}-\cos \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} x, i}+\right.\\ \left.\left(\cos \alpha \sin \alpha_{\mathrm{p}, i}+\sin \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} y, i}\right] \ddot{\alpha}_{\mathrm{p}, i} . \end{gathered} $

将摆动惯性力在弹道系y方向的投影P_ty代入式(11)可得

$ \Delta P_{\mathrm{t} y}=\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{21, i} \Delta \ddot{\alpha}_{\mathrm{p}, i}+\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{22, i} \Delta \alpha_{\mathrm{p}, i}+d_{23} \Delta \alpha . $

(21)

其中：

$ \begin{gathered} d_{21, i}=\left(\cos \alpha \cos \alpha_{\mathrm{p}, i}-\sin \alpha \sin \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} x, i}- \\ \left(\cos \alpha \sin \alpha_{\mathrm{p}, i}+\sin \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} y, i} ,\\ d_{22, i}=\left[-\left(\cos \alpha \sin \alpha_{\mathrm{p}, i}+\sin \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} x, i}+\right.\\ \left.\left(\sin \alpha \sin \alpha_{\mathrm{p}, i}-\cos \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} y, i}\right] \ddot{\alpha}_{\mathrm{p}, i}, \\ d_{23}= \sum\limits_{i=1}^{n_{\mathrm{p}}}\left[-\left(\cos \alpha \sin \alpha_{\mathrm{p}, i}+\sin \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} x, i}+\right. \\ \left.\left(\sin \alpha \sin \alpha_{\mathrm{p}, i}-\cos \alpha \cos \alpha_{\mathrm{p}, i}\right) S_{\mathrm{p} y, i}\right] \ddot{\alpha}_{\mathrm{p}, i}. \end{gathered} $

将摆动惯性力矩在本体系z方向的投影P_rz代入式(11)可得

$ \Delta P_{\mathrm{r} z}=\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{31, i} \Delta \ddot{\alpha}_{\mathrm{p}, i}+\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{32, i} \Delta \alpha_{\mathrm{p}, i} . $

(22)

其中：

$ \begin{aligned} & d_{31, i}=r_{\mathrm{cp} x, i}\left(\cos \alpha_{\mathrm{p}, i} S_{\mathrm{p} x, i}-\sin \alpha_{\mathrm{p}, i} S_{\mathrm{p} y}\right)+ \\ & r_{\mathrm{cp} y, i}\left(\sin \alpha_{\mathrm{p}, i} S_{\mathrm{p} x, i}+\cos \alpha_{\mathrm{p}, i} S_{\mathrm{p} y, i}\right)+J_{\mathrm{pzz}, i}, \\ & d_{32, i}=\left[\left(\cos \alpha_{\mathrm{p}, i} r_{\mathrm{cp} y, i}-\sin \alpha_{\mathrm{p}, i} r_{\mathrm{cp} x, i}\right) S_{\mathrm{p} x, i}-\right. \\ & \left.\quad\left(\cos \alpha_{\mathrm{p}, i} r_{\mathrm{cp} x, i}+\sin \alpha_{\mathrm{p}, i} r_{\mathrm{cp} y, i}\right) S_{\mathrm{p} y, i}\right] \ddot{\alpha}_{\mathrm{p}, i}. \end{aligned} $

式中J_{pzz, i}为第i个舵面相对舵面系z轴的转动惯量。

将摆动模态力在本体系投影的第j个分量代入式(11)可得

$ \Delta P_{\mathrm{f}, j}=\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{41, i} \Delta \ddot{\alpha}_{\mathrm{p}, i}+\sum\limits_{i=1}^{n_{\mathrm{p}}} d_{42, i} \Delta \alpha_{\mathrm{p}, i} . $

(23)

其中：

$ \begin{aligned} d_{41, i}&=\sum\limits_{i=1}^{n_{\mathrm{p}}}\left[\varphi_{j y, i}^{\mathrm{r}}\left(\cos \alpha_{\mathrm{p}, i} S_{\mathrm{p} x, i}-\sin \alpha_{\mathrm{p}, i} S_{\mathrm{p} y, i}\right)-\right. \\ & \left.\varphi_{j x, i}^{\mathrm{r}}\left(\sin \alpha_{\mathrm{p}, i} S_{\mathrm{p} x, i}+\cos \alpha_{\mathrm{p}, i} S_{\mathrm{p} y, i}\right)\right], \\ d_{42, i}&=\sum\limits_{i=1}^{n_{\mathrm{p}}}\left[-\varphi_{j x, i}^{\mathrm{r}}\left(\cos \alpha_{\mathrm{p}, i} S_{\mathrm{p} x, i}-\sin \alpha_{\mathrm{p}, i} S_{\mathrm{p} y, i}\right)-\right. \\ & \left.\varphi_{j y, i}^{\mathrm{r}}\left(\sin \alpha_{\mathrm{p}, i} S_{\mathrm{p} x, i}+\cos \alpha_{\mathrm{p}, i} S_{\mathrm{p} y, i}\right)\right] \ddot{\alpha}_{\mathrm{p}, i} . \end{aligned} $

2.4 与航天工程中常用模型的对比

文[17]中建立的航天工程中常用的飞行器纵向动力学方程如下：

$ \begin{gathered} \Delta \dot{\theta}= c_{1} \Delta \alpha+c_{2} \Delta \theta+c_{4} \Delta \dot{\varphi}+c_{3} \Delta \delta_{\varphi}+ \\ c_{3}^{\prime \prime} \Delta \ddot{\delta}_{\varphi}+c_{1}^{\prime} \sum\limits_{k} \alpha_{w_{k}}+\bar{F}_{y}, \end{gathered} $

(24)

$ \begin{gathered} \Delta \ddot{\varphi}= -b_{1} \Delta \dot{\varphi}-b_{2}\left(\Delta \alpha+\sum\limits_{k} \alpha_{w_{k}}\right)- \\ b_{3} \Delta \delta_{\varphi}-b_{3}^{\prime \prime} \Delta \ddot{\delta}_{\varphi}-\bar{M}_{z} . \end{gathered} $

(25)

式中：δ_φ为操纵机构摆动发动机的摆角，α_wk为风干扰产生的附加攻角，F_y与M_z分别为结构干扰与发动机干扰的合成干扰力与力矩系数。

将式(14)与(24)对比，本文建立的平动动力学方程(14)中出现了与姿态运动相关的项$a_{22} \Delta \dot{\omega}_{\mathrm{c}z}$。将式(15)与(25)对比，本文建立的姿态动力学方程(15)中出现了与轨道运动相关的项$a_{32} \Delta \dot{V}$、$a_{33} \Delta \dot{\theta}$。这些姿轨耦合项的系数均与飞行器相对本体系的总静矩有关，当本体系原点置于飞行器质心时均取零值。但对于具有柔性主体结构、带有较重液体燃料的飞行器，受结构弹性振动、液体燃料晃动与消耗等因素的影响，飞行器的实际质心位置会随时间变化，与本体系原点不再重合，使静矩不再为零。保留上述各项，可以更充分地考虑由于静矩变化而产生的姿轨耦合对飞行器动力学特性的影响。此外，式(24)中的$c_{1} \Delta \alpha 、c_{2} \Delta \theta 、c_{4} \Delta \dot{\varphi}$与式(25)中的$b_{1} \Delta \dot{\varphi} 、b_{2}\left(\Delta \alpha+\sum\limits_{k} \alpha_{w_{k}}\right)$均由气动力、发动机推力或重力产生，将分别包含在式(14)与(15)中的主动力偏量与ΔF_y与ΔT_z中。

式(24)中的$c_{3}^{\prime \prime} \Delta \ddot{\delta}_{\varphi}$与式(25)中的$b_{3}^{\prime \prime} \Delta \ddot{\delta}_{\varphi}$分别为操纵机构摆动惯性力与力矩项，其系数表达式分别为：

$ c_{3}^{\prime \prime}=\frac{n_{\varphi} m_{\mathrm{R}} l_{\mathrm{R}}}{m V}, $

(26)

$ b_{3}^{\prime \prime}=\frac{1}{J_{z}}\left[n_{\varphi} m_{\mathrm{R}} l_{\mathrm{R}}\left(x_{\mathrm{R}}-x_{\varepsilon}\right)+n_{\varphi} J_{\mathrm{R}}\right] . $

(27)

式中：n_φ为控制俯仰运动的摆动发动机台数，与本文的n_p对应；m_R为单台摆动发动机的质量，l_R为摆动发动机质心至摆轴的距离，则m_Rl_R即表示摆动发动机相对摆轴的静矩，与本文的S_px对应；x_R与x_z分别为摆动发动机提点与火箭质心至理论尖端的距离，则x_R－x_z即为摆动发动机提点至火箭质心的距离，与本文的r_cpx对应；J_R为摆动发动机绕摆轴的转动惯量，与本文的J_pzz对应。

当将攻角和舵偏角视为小量时，与式(26)中c″₃对应的本文中的系数d_{21, i}/a₂₁可简化为

$ \frac{d_{21, i}^{\prime}}{a_{21}^{\prime}}=\frac{S_{\mathrm{p}x, i}}{m V} . $

(28)

由本文与文[17]的符号对应关系可得，式(28)与(26)等价。但是，将式(28)代入式(14)后与式(24)对比可发现，式(14)中的摆动惯性力项$d_{21, i}^{\prime} \Delta \ddot{\alpha}_{\text{p}, i}$与式(24)中的对应项$c_{3}^{\prime \prime} \Delta \ddot{\delta}_{\varphi}$相差一个负号，这是由于本文使用的坐标系定义使静矩S_px取负值，而文[17]中与之对应的静矩m_Rl_R为正值。

当将攻角和舵偏角视为小量时，与式(27)中b″₃对应的本文中的系数d_{31, i}/a₃₁可简化为

$ \frac{d_{31, i}^{\prime}}{a_{31}^{\prime}}=\frac{1}{J_{z z}}\left(r_{\mathrm{cp}x, i} S_{\mathrm{p}x, i}+r_{\mathrm{cp}y, i} S_{\mathrm{p} y, i}+J_{\mathrm{p} z z, i}\right) . $

(29)

将式(29)与(27)对比可知，本文给出的摆动惯性力矩项经简化后比文[17]的结果多出一项$r_{\mathrm{cp}y, i} S_{\mathrm{py}, i} \Delta \ddot{\alpha}_{\mathrm{p}, i}$。该项是由摆动惯性力在本体系x轴方向的分量产生的力矩，当摆动发动机与火箭本体的连接点位于火箭的纵向对称面x₁O₁z₁平面(r_cpy=0)，或摆动发动机的质心位于其随体系的x_pO_pz_p平面(S_py=0)时，该项力矩为零。考虑到运载火箭摆动发动机提点至火箭质心的距离远大于火箭的横截面半径(|r_cpx|≫|r_cpy|)，该力矩对于运载火箭亦可忽略。

与文[17]相比，本文给出的摆动惯性力与力矩的线性化表达式中，不仅含有舵偏角加速度的增量$\Delta \ddot{\alpha}_{\text{p}, i}$，还存在舵偏角的增量Δα_{p, i}与攻角的增量Δα。由式(17)与(18)可知，虽然这两个公式描述的摆动惯性力与力矩是由摆动角加速度产生的，但由于存在坐标转换以及变矢量的相对导数与绝对导数的代换关系，摆动惯性力与力矩在弹道系或本体系中的分量不仅是摆动角加速度的函数，也与飞行器的攻角、侧滑角、速度倾斜角、姿态角速度以及舵面摆动的角度与角速度有关。故摆动惯性力与力矩在相应坐标系的分量的增量表达式中，应包含摆动角加速度以及上述各角度与角速度的增量。与航天工程中常用模型相比，本文建立的模型考虑了飞行器攻角与舵偏角的扰动对舵面摆动惯性力与力矩在相应坐标系分量的影响。

3 算例分析

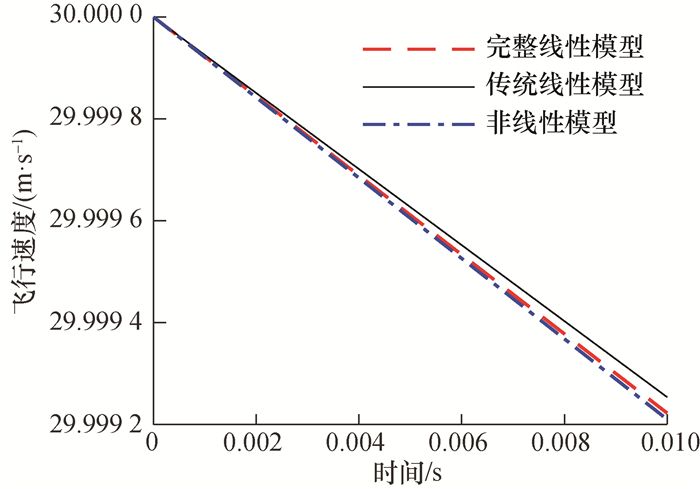
以由弹性本体和刚体舵面组成的刚柔耦合飞行器为例，采用系数冻结法在未扰动弹道上选取的特征点附近对线性化模型进行仿真分析。在选取的未扰动弹道特征点处，飞行器的速度为30 m/s，攻角为25°，舵偏角为15°，舵偏角加速度为150(°)/s²。将本文推导的未作角度简化的线性化模型记为完整线性模型，将把攻角和舵偏角均视为小量、摆动惯性力与力矩仅保留摆动角加速度的增量项、不考虑由静矩变化产生的姿轨耦合项的线性化模型记为传统线性模型。以原始的非线性模型直接计算得到的扰动运动变量值作为准确值，将线性化模型计算得到的运动变量增量值与对应时刻未扰动运动变量值的和作为线性化模型求解的扰动运动变量值。在无外力作用、耦合惯性力只保留舵面摆动惯性力、力矩与模态力，对舵偏角与舵偏角加速度施加5%的扰动量的条件下，完整线性模型、传统线性模型与非线性模型求解得到的飞行速度响应如图 1所示。

由图 1的速度响应曲线对比可知，完整线性模型的仿真结果比传统线性模型的更接近非线性模型的结果，即其仿真精度更高。以下以完整线性模型的仿真结果作为参考值，对比不同简化条件下线性化模型的仿真结果差异。

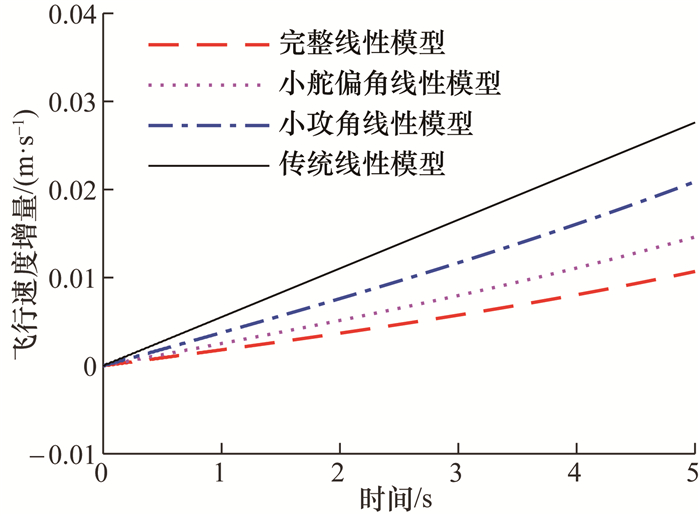
将仅把攻角或舵偏角视为小量的线性化模型分别记为小攻角线性模型和小舵偏角线性模型。在与上文相同的仿真条件下，小攻角线性模型、小舵偏角线性模型、传统线性模型与完整线性模型求解得到的飞行速度增量响应如图 2所示。

由图 2的速度增量响应曲线对比可知，在大攻角与大舵偏角条件下，简化的线性模型与完整线性模型的仿真结果差异明显，且将攻角和舵偏角均视为小量的模型的仿真误差最大。

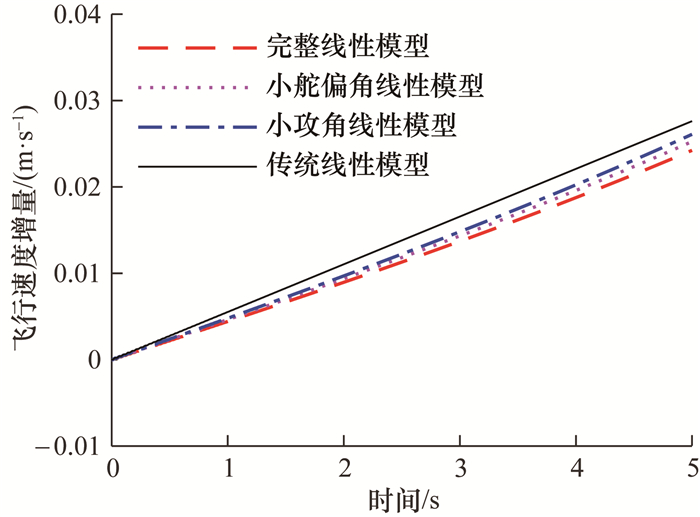
将未扰动弹道特征点的攻角与舵偏角均改为5°，其他条件保持不变，仍对舵偏角与舵偏角加速度施加5%的扰动量，小攻角线性模型、小舵偏角线性模型、传统线性模型与完整线性模型求解得到的飞行速度增量响应如图 3所示。

由图 3的速度增量响应曲线对比可知，当飞行器的攻角和舵偏角均较小时，简化的线性模型与完整线性模型的仿真结果较为接近，此时将攻角或舵偏角作为小量处理均不会导致线性化模型的仿真结果产生较大误差。

4 结论

本文研究了大攻角与大舵偏角条件下刚柔耦合飞行动力学模型的线性化问题，建立了高精度的飞行器纵向动力学线性化模型。与航天工程中常用模型相比，本文给出的操纵机构摆动惯性力与力矩的线性化表达式更为精细，可以精确描述飞行器攻角与舵偏角的扰动对摆动惯性力与力矩在相应坐标系分量的影响。

但本文尚未给出包括气动力在内的主动力的线性化表达式。在大攻角条件下，飞行器所受气动力可能表现出强非线性特征，此时是否仍能仅将其Taylor展开后的一阶项作为线性化结果有待进一步研究。