2. 北京工业大学 北京人工智能研究院, 北京计算智能与智能系统重点实验室, 北京 100124
2. Beijing Key Laboratory of Computational Intelligence and Intelligent System, Beijing Institute of Artificial Intelligence, Beijing University of Technology, Beijing 100124, China
为了方便处理日益复杂且危险的任务,四足机器人技术的发展愈发成熟,与仿人、六足机器人[1-2]相比,其独特的仿生结构在便于建模仿真的同时也能够产生更快速的运动,因此对四足机器人运动技能的研究受到广泛关注 [3],如波士顿动力公司的SpotMini、麻省理工学院的Cheetah[4-5]、苏黎世联邦理工学院的ANYmal[6]等。运动技能是指让四足机器人能够像动物一样自由运动,其主要评价指标为平衡性和动态运动能力、运动协调能力、在运动过程中对自身的控制能力,以及面对复杂地形时的运动稳定能力等。在深度强化学习技术逐渐兴起后,四足机器人的运动控制也由传统步态调制向自主学习转化[7],强化学习通过启发式方法让四足机器人与环境进行不断交互[8],对四足机器人状态以及当前采取的动作进行奖励或者惩罚,使四足机器人具有自我学习的能力[9]。然而针对四足机器人在复杂地形环境中的运动技能学习方面,由于高维连续状态的动作空间的存在,智能体与环境交互反馈耗时较长,训练策略僵化;并且机器人在与环境交互过程中具有随机性,训练效果会变得不稳定,同样导致训练时间的延长。针对这一问题的优化方向主要分为2类,一类是将步态调制算法当作教师信号的强化学习分层控制,通过下层控制器引导上层强化学习的训练方向[10-11],如Zhang等[12]提出一种基于轨迹跟踪器的分层强化学习控制算法,在四足机器人运动轨迹跟踪任务中表现出较好的效果;但该类算法需要针对特定的训练场景以及步态进行建模,过程较为复杂,削弱了算法的适用性。另一类是通过启发式算法(如遗传算法[13]、进化策略[14]等)对强化学习参数进行优化,可以减小强化学习算法对噪声和扰动的敏感性,如As等[15]通过遗传算法优化DDPG算法完成工业生产任务的技能学习;但该类算法的效果依赖于初始解和参数的选取,存在梯度计算,大大降低了算法的训练效率。
基于自适应协方差矩阵进化策略(covariance matrix adaptation evolutionary strategy, CMA-ES)是一种随机化的黑箱优化算法[16]。相比于步态调制算法,CMA-ES无须针对特定场景进行建模,大大减少了算法使用的复杂度;与传统的启发式算法不同,CMA-ES无须使用梯度计算就能对目标函数进行优化,可以自适应地调整参数,避免了算法对参数的依赖问题。
因此,本文提出一种基于优化并行的软演员-评论家(optimized parallelism soft actor-critic, OP-SAC) 算法,本算法通过CMA-ES与软演员-评论家(SAC)算法对四足机器人进行多线程的并行优化,采用知识共享策略,将二者的预测结果共同放入经验池中,降低经验池中数据的耦合性,通过知识继承将进化策略的结果继承到强化学习阶段,在训练方向上进行有效引导。本文设计仿真实验,将地形环境从平地扩展至斜坡进行算法训练。实验结果表明, 与其他基于进化策略的SAC算法相比,本文提出的方法训练出来的四足机器人能够以标准的对角小跑步态在斜坡地形上保持姿态稳定地快速协调运动,并且算法在训练效率上有大幅提高。
1 相关工作 1.1 协方差矩阵自适应进化策略CMA-ES是一种随机优化算法,利用正态分布
| $ \mathcal{N}\left(m^{(g)}, C^{(g)}\right) \sim m^{(g)}+\boldsymbol{B} \boldsymbol{D} \mathcal{N}(0, \boldsymbol{I}) . $ | (1) |
其中:m(g)表示均值,是第g代搜索分布的期望,m(g)∈Rn; C(g)是第g代的协方差矩阵,B为标准正交基,BBT=I, D为对角矩阵,D2=I。
进一步得到子代采样的基本公式为
| $ \begin{gather*} x_{k}^{(g+1)} \sim m^{(g)}+\sigma^{(g)} \boldsymbol{B} \boldsymbol{D} \mathcal{N}(0, \boldsymbol{I}), \\ k=1, 2, \cdots, \lambda . \end{gather*} $ | (2) |
其中:xk(g+1)是第g+1代的第k子代,xk(g+1)∈Rn, σ(g)是第g代的全局步长,λ≥2。
算法通过“(μ, λ)-ES”机制进行子代选择和重组,首先对种群中每个子代进行适应度计算,选择适应度最高的前μ个子代作为下一代(第g+1代)的亲本,利用这些优质个体的信息加权平均计算均值,如式(3)所示。
| $ m^{(g+1)}=\sum\limits_{i=1}^{\mu} \omega_{i} x_{i: \lambda}^{(g+1)}, \sum\limits_{i=1}^{\mu} \omega_{i}=1 . $ | (3) |
其中:μ为子代种群大小,μ≤λ; xi: λ(g+1)为第g+1代粒子中适应度最高的前μ个子代;ωi为第i个样本被分配的权重。适应度高的粒子会分配更大的样本权重,按照正态分布特性生成新的种群,具体的更新公式如式(4)所示。
| $ m^{(g+1)}=m^{(g)}+c_{m} \sum\limits_{i=1}^{\mu} \omega_{i}\left(x_{i: \lambda}^{(g+1)}-m^{(g)}\right) . $ | (4) |
其中:cm为种群迭代的更新系数,用来控制算法更新速度。这种更新方式可以保证下一代种群的中心是向着最优点的方向前进。算法中协方差矩阵的更新也是非常重要的。协方差矩阵采用“秩—1”更新和“秩—μ”更新结合的方式。
若采用“秩—1”更新,C(g)的更新公式如下:
| $ \boldsymbol{C}^{(g+1)}=\left(1-c_{1}\right) \boldsymbol{C}^{(g)}+c_{1} \boldsymbol{y}_{i: \lambda}^{(g+1)}\left(\boldsymbol{y}_{i: \lambda}^{(g+1)}\right)^{\mathrm{T}} . $ | (5) |
其中:c1为矩阵更新系数,yi: λ(g+1)是将第g+1种群进行正交操作后得到的子代种群。
若采用“秩—μ”更新,C(g)的更新公式如下:
| $ \begin{gather*} \boldsymbol{C}^{(g+1)}=\left(1-c_{\mu} \sum\limits_{i=1}^{\lambda} \omega_{i}\right) \boldsymbol{C}^{(g)}+ \\ c_{\mu} \sum\limits_{i=1}^{\lambda} \omega_{i} \boldsymbol{y}_{i: \lambda}^{(g+1)}\left(\boldsymbol{y}_{i: \lambda}^{(g+1)}\right)^{\mathrm{T}} . \end{gather*} $ | (6) |
其中cμ为矩阵更新系数。
将式(4)和(5)结合起来得到C(g)的更新公式如下:
| $ \begin{gather*} \boldsymbol{C}^{(g+1)}=\left(1-c_{1}-c_{\mu} \sum\limits_{i=1}^{\lambda} \omega_{i}\right) \boldsymbol{C}^{(g)}+ \\ c_{1} \boldsymbol{y}_{i: \lambda}^{(g+1)}\left(\boldsymbol{y}_{i: \lambda}^{(g+1)}\right)^{\mathrm{T}}+c_{\mu} \sum\limits_{i=1}^{\lambda} \omega_{i} \boldsymbol{y}_{i: \lambda}^{(g+1)}\left(\boldsymbol{y}_{i: \lambda}^{(g+1)}\right)^{\mathrm{T}} . \end{gather*} $ | (7) |
当c1=0时,更新规则退化为“秩—μ”更新,当cμ=0时,更新规则退化为“秩—1”更新,这种更新方式既有效利用了连续2代均值的偏差关系,又充分利用了种群中的信息,提高了算法的适用性。
CMA-ES采用累积步长控制,如果演化路径比预期的长,则步长增加;如果演化路径比预期的短, 则步长减小;在理想条件下,选择不会偏向演化路径的长度,并且该长度等于随机选择下的预期长度。因此步长的更新公式如下:
| $ \sigma^{(g+1)}=\sigma^{(g)} \exp \left[\frac{c_{\sigma}}{b_{\sigma}}\left(\frac{\left\|p_{\sigma}^{(g+1)}\right\|_{2}}{E\|N(0, 1)\|_{2}}-1\right)\right] . $ | (8) |
其中:cσ为步长更新系数,bσ为阻尼系数,pσ(g+1)为CMA-ES的演化路径,采用Euclid范数来表示演化路径的长度,E||N(0, 1)||2为演化路径的期望长度。
1.2 SAC算法SAC算法[17-18]是以Actor-Critic框架为基础,融合Soft Q-Learning中最大熵原理[19]的策略梯度算法,该算法与标准强化学习(RL)的不同之处在于将策略的熵整合到奖励目标中,如式(9)所示,通过在策略边界范围内用策略的期望熵来扩充目标从而支持随机策略,以期望同时最大化预期回报来鼓励智能体尽可能学习一个随机行为策略,避免智能体陷入局部最优策略。
| $ J(\theta)=\sum\limits_{t=1}^{T} E_{\left(s_{t}, a_{t}\right) \sim \rho_{\pi_{\theta}}}\left[r\left(s_{t}, a_{t}\right)+\alpha H\left(\pi_{\theta}\left(\cdot \mid s_{t}\right)\right)\right]. $ | (9) |
其中:J(θ)为SAC算法的优化目标;E(st, at)~ρπθ为奖励值的期望;ρπθ为智能体的策略边界,即智能体状态与动作可能取到的边界值;st, at分别为智能体在t时刻的状态和动作;r(st, at)为状态st下采取动作at获得的奖励;αH(πθ(·|st))是关于策略的熵;α为温度系数,主要定义熵在目标函数中的重要性。
在SAC算法中使用策略网络与价值网络分别表示基于最大熵的随机策略与状态动作值函数。SAC算法不直接对Soft Q函数、状态值函数和策略的收敛性进行评估和改进,将Soft Q函数和状态值函数建模为神经网络,将策略建模为具有由神经网络给出均值和协方差的Gauss分布。并交替使用随机梯度下降优化3个网络,分别是策略网络π、价值网络Q以及目标价值网络Q′。因此SAC算法主要学习以下目标函数:
1) 参数θ的Soft Q函数Qθ。Soft Q函数的参数可以通过Soft Bellman残差来训练,其目标函数为
| $ J_{Q}(\theta)=E_{\left(s_{t}, a_{t}\right) \sim D}\left[\frac{1}{2}\left(Q_{\theta}\left(s_{t}, a_{t}\right)-\hat{Q}\left(s_{t}, a_{t}\right)\right)^{2}\right]. $ | (10) |
其中:D为缓存器中采样的状态动作分布,
| $ \begin{gathered} \hat{\nabla}_{\theta} J_{Q}(\theta)=\nabla_{\theta} Q_{\theta}\left(s_{t}, a_{t}\right) \cdot \\ \left(Q_{\theta}\left(s_{t}, a_{t}\right)-r\left(s_{t}, a_{t}\right)-\gamma V\left(s_{t+1}\right)\right) . \end{gathered} $ | (11) |
其中:
2) 带有参数ϕ的策略πϕ。在Soft策略迭代过程中,为了能够保证新策略能够在软值上得到改善,选择使新、旧策略的KL散度值DKL最小的策略作为新策略。
| $ \pi_{\mathrm{new}}=\underset{\pi^{\prime} \in \varPi}{\operatorname{argmin}} D_{\mathrm{KL}}\left(\pi^{\prime}\left(\cdot \mid s_{t}\right) \| \frac{\exp \left(Q^{\pi_{\text {old }}}\left(s_{t}, \cdot\right)\right)}{Z^{\pi_{\text {old }}}\left(s_{t}\right)}\right) . $ | (12) |
其中:π′(·|st)为当前时刻智能体采取的策略,Zπold(st)为关于旧策略的归一化函数,Qπold(st, ·)为旧策略的价值函数。
但由于策略由神经网络估计得出,在进行参数更新的时候可进行微分,因此可以利用重参数化技巧重新定义策略的部分参数,降低神经网络估计出来的方差。以动作at为例,如式(13)所示,将其改写为由参数εt和st表示的函数fϕ。
| $ a_{t}=f_{\phi}\left(\varepsilon_{t}, s_{t}\right) . $ | (13) |
因此目标函数可以改写为式(14)。
| $ \begin{gather*} J_{\pi}(\phi)=E_{s_{t} \sim D, \varepsilon_{t} \sim N}\left\{\left[\log \pi_{\phi}\left(f_{\phi}\left(\varepsilon_{t}, s_{t}\right) \mid s_{t}\right)-\right.\right. \\ \left.\left.Q_{\theta}\left(s_{t}, f_{\phi}\left(\varepsilon_{t}, s_{t}\right)\right)\right]\right\} . \end{gather*} $ | (14) |
其中πϕ为参数化为ϕ的策略。
通过随机梯度下降对参数进行如下更新:
| $ \begin{gather*} \hat{\nabla}_{\phi} J_{\pi}(\phi)=\nabla_{\phi} \log \pi_{\phi}\left(a_{t} \mid s_{t}\right)+ \\ \left(\nabla_{a_{t}} \log \pi_{\phi}\left(a_{t} \mid s_{t}\right)-\nabla_{a_{t}} Q\left(s_{t}, a_{t}\right)\right) \nabla_{\phi} f_{\phi}\left(\varepsilon_{t}, s_{t}\right) . \end{gather*} $ | (15) |
其中:
除此之外,由于熵在任务之间和训练过程中都可能发生不可预测的变化,需要根据训练过程中的状态、策略等相关条件进行动态调整,通过删除策略、Soft Q函数和温度系数三者中的时间相关性来预测出平稳策略的近似值。因此除了价值网络和策略网络,该算法还通过最小化(10)中的对偶目标来学习α。
| $ J(\alpha)=E_{a_{t} \sim \pi_{t}}\left[-\alpha \log \pi_{t}\left(a_{t} \mid s_{t}\right)-\alpha H\right] . $ | (16) |
其中H表示探索过程中的熵。
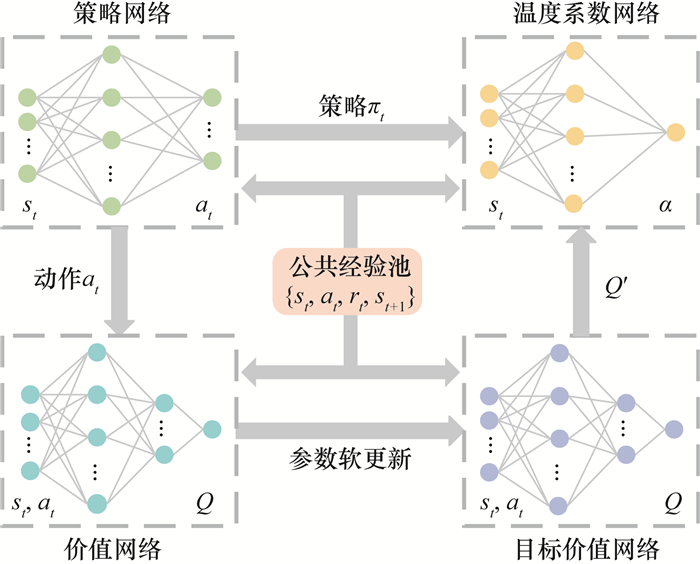
整个SAC算法的流程如图 1所示,智能体通过获取当前时刻状态st,经过策略网络生成所采取动作的分布,经采样得到对应动作at,再通过环境进入到下一个时间步的状态st+1和奖励值rt,通过价值网络得到对应的Q值与目标Q值Q′,同时将策略输入温度系数网络中预测出当前时刻的温度系数α。将上述过程采集到的数据{st, at, rt, st+1}存入训练样本池中,当样本池中样本数量大于256时,更新各个网络的参数,重复上述过程直到算法收敛。
|
| 图 1 SAC算法的训练流程图 |
2 基于OP-SAC算法的四足机器人运动技能学习
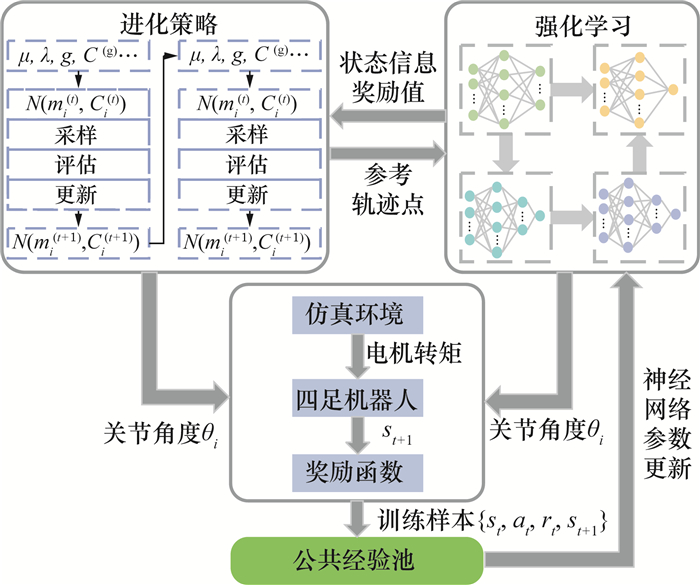
提高强化学习训练效率,使训练效果更加稳定是强化学习优化的目标之一,传统的启发式算法对强化学习训练效果的影响依赖于初始解与参数的选取,在计算上存在梯度计算,大大降低了算法的训练效率。为克服上述问题,本文提出一种基于优化并行的算法OP-SAC,该算法的整体结构如图 2所示,算法主要包含进化策略部分与强化学习部分,经过进化策略与强化学习的并行训练后得到机器人的期望关节角度,经过仿真环境使四足机器人完成动作后得到训练样本,存入样本{st, at, rt, st+1}的公共经验池中。
|
| 图 2 OP-SAC算法的整体框图 |
为验证所提算法的有效性,选用A1型机器人进行仿真验证,仿真模型来源于文[13]。该四足机器人的单腿有3个自由度,每个自由度通过电机输出力矩实现位置控制。足端设置有接触传感器,通过接触传感器的触发来判断四足机器人的运动状态是摆动相还是支撑相,通过接触点的数量判断四足机器人的步态类型。机器人内置惯性测量单元(IMU),用来测量位姿和加速度,同时设置距离传感器,测量机器人在运动过程中X、Y、Z轴上的位移。四足机器人的关键参数如表 1所示。
| 参数 | 取值 |
| 站立尺寸(长×宽×高)/(mm×mm×mm) | 370×270×295 |
| 质量/kg | 11 |
| 关节自由度 | 12 |
| 髋关节动作空间/(°) | -46~46 |
| 摆动关节动作空间/(°) | -60~240 |
| 膝关节动作空间/(°) | -154.5~-52.5 |
整个算法主要由2部分组成(见图 2),包括进化策略部分和强化学习部分。
在进化策略部分,本算法采用CMA-ES作为进化策略对四足机器人步态进行优化,首先将机器人参数信息与地形信息作为参数输入到算法中,然后使用CMA-ES算法得到当前环境下的参考轨迹点,并将其与上一回合训练得到的参考轨迹加权组合成一组新的轨迹集合,更新CMA-ES参数之后新的步态轨迹如式(17)所示。
| $ \text { point }_{\text {new }}=\varphi_{1} \text { point }_{t}+\varphi_{2} \text { point }_{t+1} . $ | (17) |
其中:pointt和pointt+1分别为当前时间步和上一时间步训练出来的参考轨迹点;φ1、φ2分别是新、旧参考轨迹点的融合的系数,二者之和为1。将新的参考轨迹输入SAC算法的训练回合中,更新现有SAC算法的神经网络参数得到新的奖励值与新的状态信息,通过选择选出适应度最高的μ个子代,重复上述过程,直到得出唯一最优解,并将其存储到缓冲区。
在强化学习部分,采用SAC算法对四足机器人进行训练,算法模型的状态空间维度为37,可表示为s={ϕi, ωi, ci, di, ϕp, ωp},包含各个关节电机的旋转角度ϕi和角速度ωi各12项,4项足端接触检测ci,3项距离传感器数据di,IMU测得的机器人姿态角ϕp与角速度ωp各3项。动作空间维度可表示为a={θ1, θ2, …, θi},此处i=12,θi分别为各个自由度电机需旋转的角度。策略网络的输入为状态观测空间的数据元组s,输出为四足机器人动作分布的均值与方差,可用于生成下一步的动作。当机器人做出动作之后进入下一时间步的状态,得到新的状态观测值,将其作为策略网络与价值网络的输入来预测下一步动作与Q值,同时更新网络参数。算法的最终目标为让四足机器人学会以最高速度稳定地在斜坡地形上行走[20],参考这个目标设置如下奖励函数进行模型训练。
1) 躯干速度奖励rtv。
| $ r_{t}^{v}=v_{\max }[1-\exp (-0.5 v)] . $ | (18) |
其中vmax和v分别为最大速度和当前速度。
2) 足端接触奖励rtc用于判断四足机器人行走过程中落地是否稳定,当四足机器人有2条以上的腿没有接触地面时,被认为步态不稳。
| $ r_{t}^{\mathrm{c}}=-\max \left(n_{\text {loss }}-2, 0\right) . $ | (19) |
其中nloss为四足机器人足端未接触地面的数量。
3) 姿态奖励rto控制四足机器人在行走过程中保持身体姿态稳定。
| $ r_{t}^{\rm o}=1-\tan \left[3.75\left(r^{2}+p^{2}\right)\right] . $ | (20) |
其中:r和p分别为四足机器人的偏航角和俯仰角。当四足机器人位姿出现偏差时奖励变小,偏差过大时奖励变为惩罚。
最后将所有奖励根据重要性进行加权求和,以期望训练效果达到最佳,其中R为整个奖励函数,kv、kc和ko分别为对应奖励的系数。
| $ R=k_{\mathrm{v}} r_{t}^{\mathrm{v}}+k_{\mathrm{c}} r_{t}^{\mathrm{c}}+k_{\mathrm{o}} r_{t}^{\mathrm{o}} . $ | (21) |
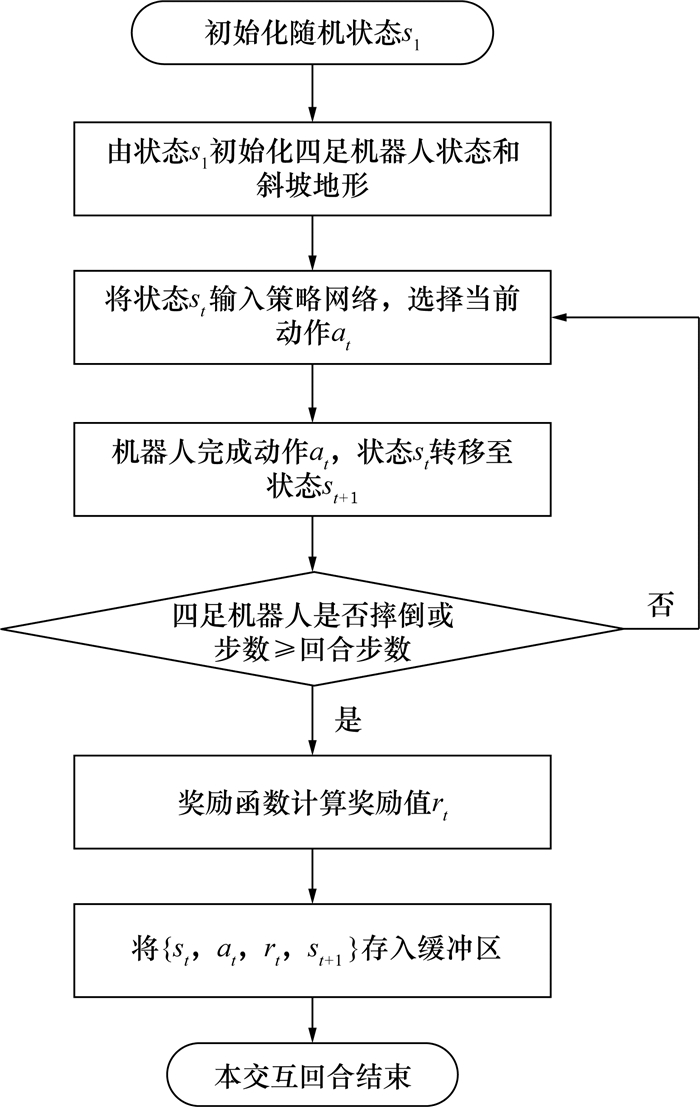
整个强化学习回合的交互过程如图 3所示。
|
| 图 3 四足机器人强化学习回合的交互过程 |
算法的整个训练过程由SAC算法与CMA-ES进行并行训练。所谓并行,是在训练过程中将强化学习和进化策略2种算法进行多线程同时训练,其中强化学习每隔50 000步将机器人当前状态与平均奖励值同步并继承给进化策略,CMA-ES训练10个回合后将参考轨迹点传递给SAC算法模块。二者只在知识共享和知识继承阶段进行策略信息传递,在此过程中,首先由SAC算法生成该回合的机器人动作与Q值,再通过奖励函数与Q值得出算法的平均奖励值,使机器人进入下一状态,将这个奖励值当作进化策略选择子代种群标准,并将此时的状态当作CMA-ES的输入,得到对应状态下的最优参考轨迹与最高适应度,经过式(17)得到新参考轨迹,将新的参考轨迹输入SAC算法训练回合中,经过迭代产生新的动作,再更新参数并将完整策略添加到经验池中,重复上述步骤,直到平均奖励值收敛。
采用知识共享策略,CMA-ES所产生的策略与强化学习的预测结果共享一个经验池,在进化学习部分,会计算CMA-ES所产生的可行解的最优部分,然后放入经验池中,降低经验池数据的耦合性。
采用知识继承策略,将CMA-ES的训练结果作为下次强化学习的输入,继承CMA-ES的最优策略在训练方向上进行有效引导,强化学习预测结果当作下次进化学习的初始化参数,学习的平均奖励值作为进化学习适应度的评价标准,避免随机初始化对进化策略产生的多余训练代价,大大改善四足机器人在复杂地形中步态学习的效率和效果。
3 实验结论 3.1 实验仿真建模本实验的仿真环境为pybullet框架,该仿真环境可以通过加载urdf文件任意构建四足机器人与地形环境,并在pytorch框架下对所提算法进行优化,然后对四足机器人进行训练。在仿真环境中设置机器人关节信息:关节间的摩擦系数为0.025;足端与地面的摩擦系数为1;仿真环境中单位时间步的间隔为2 ms;地形中斜面坡度为12°;电机的控制模式为位置控制,控制律为1.0。整个实验所用的计算机为搭载i7-9750H的笔记本电脑,无GPU加速。
为了验证所提算法的性能,本文从3个方面进行实验评估:1) 使用该算法对四足机器人步态学习进行训练,验证算法的可行性;2) 设计对比实验验证算法的优越性;3) 设计消融实验验证本文所提训练策略的有效性。
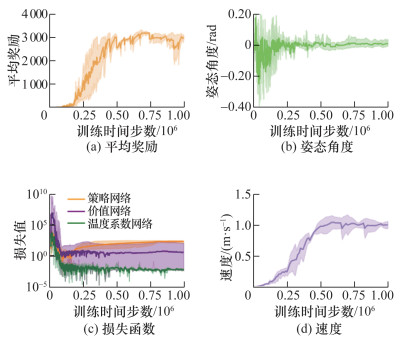
3.2 算法收敛性实验本算法在四足机器人环境中的训练结果如图 4所示,算法的训练时长为1×106个时间步,当训练至约4×105个时间步时,平均奖励值趋于收敛(见图 4a);四足机器人运动中的姿态角在训练初期来回摆动,机身不稳定;当训练稳定之后,姿态角稳定在0°左右(见图 4b),说明此时四足机器人在斜坡地形的运动策略已经训练完成,机身可以保持稳定;图 4c为训练过程中强化学习网络的损失函数变化,由图可知四足机器人在训练前期的损失函数已经收敛。训练稳定之后四足机器人的前进速度达到最大速度1.0 m/s(见图 4d)。
|
| 图 4 OP-SAC算法在四足机器人中的训练结果 |
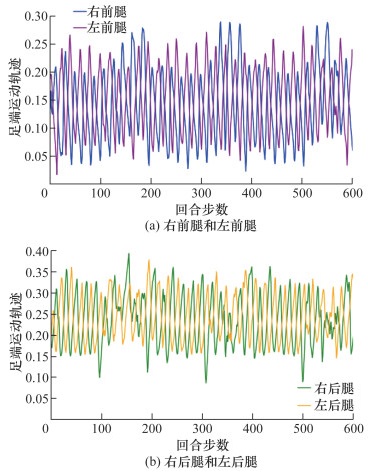
训练完成四足机器人的足端轨迹如图 5所示,由图可知,此时其左前腿(FL)与右后腿(FR)、右前腿(BR)与左后腿(BL)的运动轨迹一致,证明四足机器人的步态为对角小跑步态。由足端轨迹的高度(轨迹中最高点和最低点的绝对差值)可以看出,完成训练的四足机器人运动时抬腿高度几乎一致,说明此算法对四足机器人训练结果有效。
|
| 图 5 训练完成之后四足机器人的足端轨迹 |
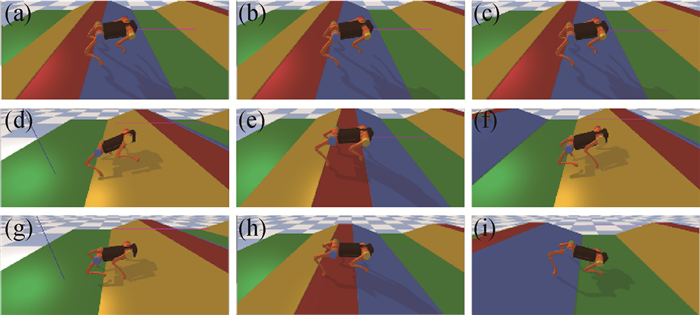
图 6a—6i所示为四足机器人在训练末期的一个回合中的运动过程,可以看出在训练末期的四足机器人已经可以稳定行走。
|
| 图 6 四足机器人在斜坡地形上的运动状态 |
3.3 对比实验 3.3.1 进化策略对比分析
实验选择SAC算法作为基础模型(baseline),将文[13]中的SAC算法、SAC算法与遗传算法(GA)的结合(SAC+GA)、SAC算法+简单进化策略(SimpleES)的结合算法(SAC+SimpleES)作为对照组,对照实验均在同一环境下进行,具体的参数设计如表 2所示。
| 参数 | 数值 |
| 策略网络学习率 | 0.000 3 |
| 评价网络学习率 | 0.000 3 |
| 折扣因子 | 0.95 |
| 软更新系数 | 0.005 |
| 批大小 | 256 |
| 回合最大步数 | 600 |
| 最大样本存储/条 | 1 000 000 |
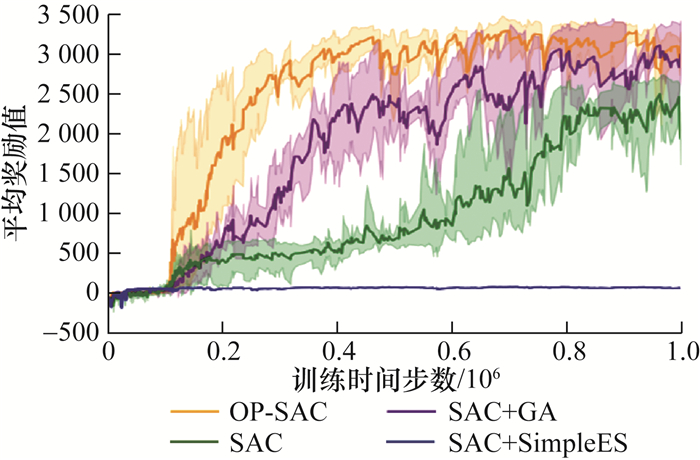
4种算法的平均奖励值对比如图 7所示。本文所提的OP-SAC算法的平均奖励值收敛最快,收敛时的值最高,在多组实验中方差最小,说明其策略的学习最为完整,策略训练效果最为稳定。
|
| 图 7 平均奖励值对比 |
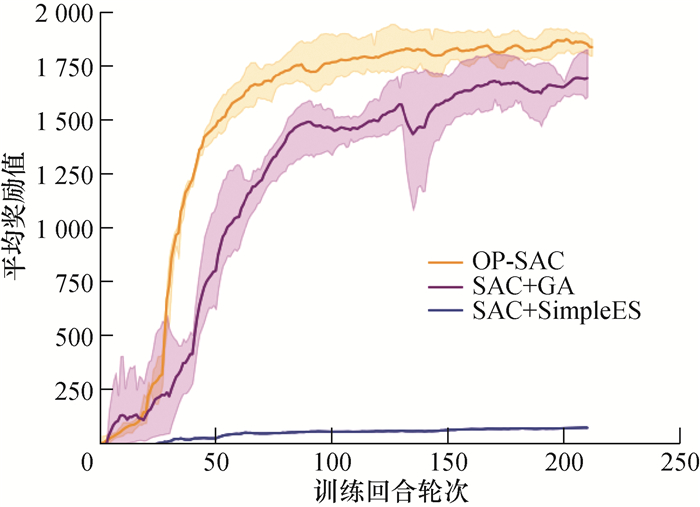
进化策略的平均奖励值对比如图 8所示,衡量进化策略在四足机器人训练过程中是否起到很好的效果。由于baseline中没有进化策略,不存在进化策略的平均奖励值,因此将OP-SAC算法与另外2种算法对比。由图可知,OP-SAC算法中进化策略的平均奖励值最高,说明CMA-ES能够有效地引导强化学习进行训练,且训练效果较为稳定。
|
| 图 8 不同进化策略的奖励对比 |
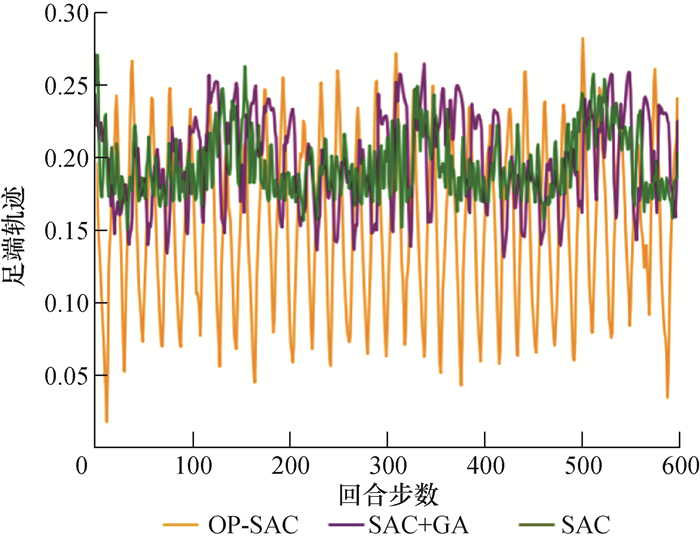
单腿的足端轨迹对比如图 9所示。由于SAC+Simple算法无法训练出稳定的策略,因此不进行足端轨迹与姿态角的对比实验。根据轨迹的高度可以看出,CMA-ES训练的步态能够正常地抬腿进行运动,而其他算法得到的步态足端抬升高度过低,存在机器人拖行现象。
|
| 图 9 四足机器人单腿足端轨迹对比 |
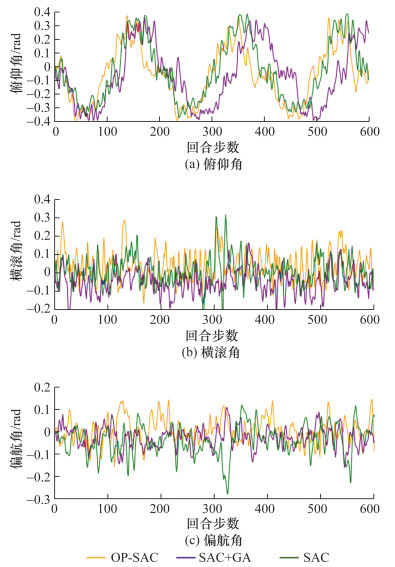
机器人姿态角对比如图 10所示,由图可知,本方法训练出来的机器人在运动过程中能够保持很小的身体晃动,整体姿态较为稳定。
|
| 图 10 四足机器人姿态角对比 |
3.3.2 主流算法对比分析
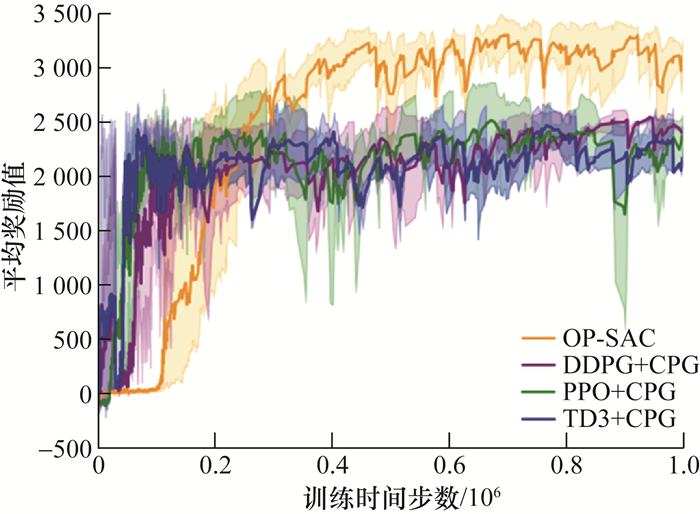
目前四足机器人运动控制中,强化学习与传统控制算法已经成为主流算法,在许多四足机器人控制中取得了优异的效果。为了进一步验证本算法的优越性,本小节设计对比实验将OP-SAC算法与3种主流强化学习(DDPG、PPO、TD3)分别结合CPG的算法进行平均奖励值的对比。由图 11可知,基于OP-SAC算法的训练至收敛速度较慢,但是收敛之后平均奖励值达到3 100,学习到的策略较为稳定,机器人能够在斜坡地形上实现稳定运动,综合运动能力较强。基于强化学习与CPG算法的训练结果平均奖励值收敛速度较快,但是收敛时的平均奖励值只达到2 000,通过仿真渲染发现机器人无法在斜坡地形上实现协调运动,虽然能够实现行走技能,但步态不和谐,没有学习到成熟的对角小跑步态。
|
| 图 11 主流算法平均奖励值对比 |
3.4 消融实验
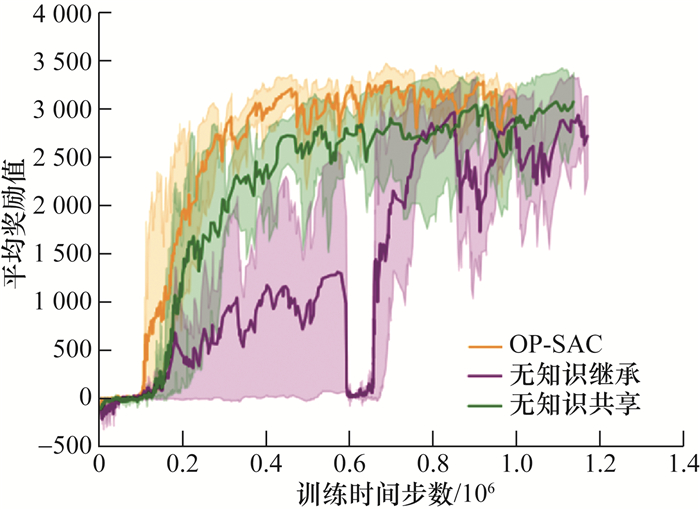
本文设计消融实验验证知识共享和知识继承策略在训练过程中对训练结果的影响,具体结果如图 12所示,当没有知识继承时,训练的速度较慢,同时在训练过程中出现平均奖励值急剧下降的问题,说明策略没有被智能体继承,影响训练效果;当没有采用知识共享时平均奖励值收敛速度较慢,在后期逐渐收敛至3 000,与本文提出的算法达到了一致。实验证明了本文提出的训练策略用于辅助四足机器人运动技能学习的有效性。
|
| 图 12 消融实验平均奖励值对比 |
4 结论
环境选择是自然界促进生物进化的方式,高等生物为了适应环境的变化,需要与环境交互并不断进化自身行为。为了使四足机器人具备更加精确的学习能力,本文受自然界生物进化的启发,提出一种基于优化并行的算法OP-SAC,将自适应协方差矩阵进化策略(CMA-ES)引入SAC算法中,使用交替训练、知识融合以及知识继承等策略强化四足机器人在复杂地形中的学习效果,提高训练效率。设计仿真实验验证算法效果。实验结果表明所提算法可以使四足机器人步态学习任务的奖励快速收敛,使其快速学会对角小跑步态;训练最初四足机器人步态不稳定,无法稳定行走,到后期可以在斜坡地面上稳定行走,四条腿的运动轨迹呈现节律信号。对比实验结果验证了本算法相比于其他主流控制算法在四足机器人运动技能学习方面性能的优越性;引入知识继承和知识共享策略可以进一步提高算法性能。后续研究有望改变四足机器人的运动状态,使其完成在复杂地形下的多种步态,同时可考虑在实物机器人中部署所提出的算法,完成实物实验。
| [1] |
付雯, 温浩, 黄俊珲, 等. 基于非线性动力学模型补偿的水下机械臂自适应滑模控制[J]. 清华大学学报(自然科学版), 2023, 63(7): 1068-1077. FU W, WEN H, HUANG J H, et al. Adaptive sliding mode control of underwater manipulator based on nonlinear dynamics model compensation[J]. Journal of Tsinghua University (Science and Technology), 2023, 63(7): 1068-1077. (in Chinese) |
| [2] |
刘志, 陈恳, 徐静. 基于模型和数据驱动的机器人6D位姿估计方法[J]. 清华大学学报(自然科学版), 2022, 62(3): 391-399. LIU Z, CHEN K, XU J. Data-driven method for 6D robot pose estimation[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(3): 391-399. (in Chinese) |
| [3] |
MCGHEE R B. Finite state control of quadruped locomotion[J]. Simulation, 1967, 9(3): 135-140. DOI:10.1177/003754976700900308 |
| [4] |
DI CARLO J, WENSING P M, KATZ B, et al. Dynamic locomotion in the MIT cheetah 3 through convex model-predictive control[C]//2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Madrid, Spain: IEEE, 2018: 1-9.
|
| [5] |
BLEDT G, POWELL M J, KATZ B, et al. MIT cheetah 3: Design and control of a robust, dynamic quadruped robot[C]//2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Madrid, Spain: IEEE, 2019: 2245-2252.
|
| [6] |
LEE J, HWANGBO J, WELLHAUSEN L, et al. Learning quadrupedal locomotion over challenging terrain[J]. Science Robotics, 2020, 5(47): eabc5986. DOI:10.1126/scirobotics.abc5986 |
| [7] |
KIM J, BA D X, YEOM H, et al. Gait optimization of a quadruped robot using evolutionary computation[J]. Journal of Bionic Engineering, 2021, 18(2): 306-318. DOI:10.1007/s42235-021-0026-y |
| [8] |
YIN F L, TANG A N, XU L W, et al. Run like a dog: Learning based whole-body control framework for quadruped gait style transfer[C]//2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Prague, Czech Republic: IEEE, 2021: 8508-8514.
|
| [9] |
SHENG J P, CHEN Y Y, FANG X, et al. Bio-inspired rhythmic locomotion for quadruped robots[J]. IEEE Robotics and Automation Letters, 2022, 7(3): 6782-6789. DOI:10.1109/LRA.2022.3177289 |
| [10] |
赵铭慧, 张雪波, 郭宪, 等. 基于分层强化学习的通用装配序列规划算法[J]. 控制与决策, 2022, 37(4): 861-870. ZHAO M H, ZHANG X B, GUO X, et al. A general assembly sequence planning algorithm based on hierarchical reinforcement learning[J]. Control and Decision, 2022, 37(4): 861-870. (in Chinese) |
| [11] |
韩连强, 陈学超, 余张国, 等. 面向离散地形的欠驱动双足机器人平衡控制方法[J]. 自动化学报, 2022, 48(9): 2164-2174. HAN L Q, CHEN X C, YU Z G, et al. Balance control of underactuated biped robot for discrete terrain[J]. Acta Automatica Sinica, 2022, 48(9): 2164-2174. (in Chinese) |
| [12] |
ZHANG X Y, GUO X, FANG Y C, et al. Reinforcement learning-based hierarchical control for path following of a salamander-like robot[C]//2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas, USA: IEEE, 2020: 6077-6083.
|
| [13] |
SHI H J, ZHOU B, ZENG H S, et al. Reinforcement learning with evolutionary trajectory generator: A general approach for quadrupedal locomotion[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 3085-3092. DOI:10.1109/LRA.2022.3145495 |
| [14] |
SHEN Y O, GAO X, LIANG Z W. Covariance matrix adaptation for multi-agent proximal policy optimization[C]//2023 35th Chinese Control and Decision Conference (CCDC). Yichang, China: IEEE, 2023: 4847-4852.
|
| [15] |
SEHGAL A, WARD N, LA H M, et al. GA+DDPG+HER: Genetic algorithm-based function optimizer in deep reinforcement learning for robotic manipulation tasks[C]//2022 Sixth IEEE International Conference on Robotic Computing (IRC). Naples, Italy: IEEE, 2022: 85-86.
|
| [16] |
DE SANT ANA P M, MARCHENKO N. Radio access scheduling using CMA-ES for optimized QoS in wireless networks[C]//2020 IEEE Globecom Workshops (GC Wkshps). Taipei, China: IEEE, 2020: 1-6.
|
| [17] |
WONG C C, CHIEN S Y, FENG H M, et al. Motion planning for dual-arm robot based on soft actor-critic[J]. IEEE Access, 2021, 9: 26871-26885. DOI:10.1109/ACCESS.2021.3056903 |
| [18] |
TANG H L, WANG A Q, XUE F, et al. A novel hierarchical soft actor-critic algorithm for multi-logistics robots task allocation[J]. IEEE Access, 2021, 9: 42568-42582. DOI:10.1109/ACCESS.2021.3062457 |
| [19] |
SHARMA K, SINGH B, HERMAN E, et al. Maximum information measure policies in reinforcement learning with deep energy-based model[C]//2021 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE). Dubai, United Arab Emirates: IEEE, 2021: 19-24.
|
| [20] |
TSOUNIS V, ALGE M, LEE J, et al. DeepGait: Planning and control of quadrupedal gaits using deep reinforcement learning[J]. IEEE Robotics and Automation Letters, 2020, 5(2): 3699-3706. DOI:10.1109/LRA.2020.2979660 |



