2. 清华大学 核能与新能源技术研究院, 北京 100084
2. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China
核电站事故可能导致大量放射性核素(包括131I、137Cs和惰性气体等裂变产物)的释放,对环境造成了严重污染。核应急工作应在事故早期对释放点位20 km内的重点区域进行快速且精确的放射性水平评估[1-6]。然而,由于核电站附近监测点空间分布不均,难以全面、有效地分析污染水平[3, 6]。因此,基于大气扩散模型建立核电站局地尺度辐射场,成为早期核事故评估的关键环节[2-3, 5-7]。
Lagrange扩散模型(粒子、烟团模型)广泛应用于放射性核素的局地尺度扩散模拟。该模型能持续追踪放射性核素在大气中的迁移轨迹,并支持高精度网格计算,避免了Euler模型的数值扩散问题[6, 8-9]。同时,Lagrange扩散模型能囊括三维时空变化的气象场,再现自然湍流效应,突破了传统Gauss烟羽模型只适用于稳定气象条件的限制,更适配包含复杂地形场景的核电站[10-12]。然而,粒子模型受制于传统计算机制(箱式计数法),通常需要大量的释放粒子[11]。虽然目前已有研究者提出了多种核密度估计法予以替代[7, 10-13],但依旧不能完全避免因网格精度产生较高的计算成本。烟团模型则基于Lagrange方法,认为释放后的污染物烟团在空间上进行平流传输,在横向和垂向服从Gauss分布的膨胀[14-15]。该处理方法使得烟团模型具有更低的计算成本,并保持了可接受的精度。
复杂地形易形成沟道流以及坡度流,导致放射性核素大气扩散出现分流以及层状分割现象[16]。因此,烟团模型必须具备分裂模式,以限制烟团在横风向的扩张,使其运动更加贴合实际风场变化,进而减少计算误差[14, 17]。国际上主要提出了2套烟团分裂方案,并分别应用到了Risø中尺度烟团(RIMPUFF)模型以及加州烟团(CALPUFF)模型中[18-20]。然而,由于各场景存在差异,启动分裂模式的阈值设定仍缺乏充分研究。
此外,风场偏差会严重恶化扩散结果[6]。因此,建立有效的风场模型也是辐射场建立的关键一环。Dong等[21-22]以及Liu等[23]基于三门核电风洞实验,验证了加州气象(CALMET)模型、质量守恒诊断风场(SWIFT)模型和RIMPUFF模型的组合效果,并指出风场诊断模型能有效反映复杂核电站的流场特征。因此,将风场诊断模型与烟团模型结合应用是必要的。
本文基于Fortran语言,开发了一款局地尺度Lagrange分裂烟团(SPUFF)扩散模型。该模型具备烟团分裂模块,具有加州气象模型CALMET的输入接口。随后,本文以CALMET模型驱动SPUFF扩散模型,基于三门核电风洞实验和福岛第一核电站事故的局地尺度模拟,分别对SPUFF扩散模型进行性能验证以及应用性评估。最后,本文在上述场景对水平分裂阈值开展了全面的敏感性分析,并推荐了参考范围,以指导烟团模型在核电站局地尺度扩散的应用。
1 研究方法 1.1 模型构建和评估本文将CALMET模型与SPUFF扩散模型进行组合应用。其中,首先基于CALMET模型采用两步法生成三维网格化诊断风场[7]。
第1步:通过输入高空气象数据,CALMET模型首先会生成初始风场,并根据地形运动学效应、坡度流以及阻挡效应进行调整。此外,在地形运动学效应调整中会应用三维散度最小化程序修正水平风场,以满足质量守恒的要求
| $ \frac{\mathrm{d} u}{\mathrm{~d} x}+\frac{\mathrm{d} v}{\mathrm{~d} y}+\frac{\mathrm{d} w}{\mathrm{~d} z} <\varepsilon . $ | (1) |
其中:u,v,w分别为网格点(x, y, z)在空间X,Y,Z方向的风速分量,m/s,在CALMET模型中,u, v具体设定在网格点上,w定义在垂直网格单元面上;ε为散度设定的最大值。
第2步:CALMET模型通过反距离法将测量数据引入第1步生成的风场,并随后进行平滑以及O'Brien调整。最后,三维散度最小化程序将再次应用,以得到最终风场。
在CALMET模型生成的诊断风场基础上,通过释放连续的Gauss烟团,利用SPUFF扩散模型针对可变释放率源项(点、体源)开展局地尺度大气扩散,以模拟放射性或非放射性的气体或气溶胶在大气中的迁移轨迹。其中,烟团的平流传输由CALMET模型输入的风场以及时间步长确定,即,
| $ x_{\mathrm{p} i}(t+\Delta t)=x_{\mathrm{p} i}(t)+u_{\mathrm{p} i} \Delta t . $ | (2) |
其中:xpi(t+Δt)和xpi(t)分别为第i个烟团在t+Δt时刻和t时刻(单位:s)的水平位置,m;upi为xpi处的风场,m/s。
SPUFF扩散模型包含了3种方法来计算烟羽抬升高度,分别依据文[26]、文[27]以及《制定地方大气污染物排放标准的技术方法》(GB/T 3840—1991)[28]。本文采用上述第3种方法来计算烟团的抬升高度。
烟团在下风距离位置d(单位:m)处的扩散参数采用了传统的Pasquill-Gifford(P-G)法[16, 18]确定。
| $ \sigma_{\mathrm{h}}=p_{\mathrm{h}} d^{q_{\mathrm{h}}}, $ | (3) |
| $ \sigma_{\mathrm{v}}=p_{\mathrm{v}} d^{q_\text{v}} . $ | (4) |
其中:σh和σv分别是水平和垂直方向的扩散参数,m;ph,qh,pv以及qv是与大气稳定度相关的参数并基于Karlsruhe-Jülich方案[16, 18]由大气稳定度(CALMET模型计算)以及释放高度共同确定。
当确定了经过Δt后的平流传输距离xpi(Δt),可由式(5)和(6)计算烟团在下一时刻所在位置xpi(t+Δt)的水平扩散参数σh(xpi(t+Δt))和垂直扩散参数σv(xpi(t+Δt))。
| $ \sigma_{\mathrm{h}}\left(x_{\mathrm{p} i}(t+\Delta t)\right)=\left(\sigma_{\mathrm{h}}\left(x_{\mathrm{p} i}(t)\right)^{\frac{1}{q_{\mathrm{h}}}}+p_{\mathrm{h}}^{\frac{1}{q_{\mathrm{h}}}} x_{\mathrm{p} i}(\Delta t)\right)^{q_{\mathrm{h}}}, $ | (5) |
| $ \sigma_{\mathrm{v}}\left(x_{\mathrm{p} i}(t+\Delta t)\right)=\left(\sigma_{\mathrm{v}}\left(x_{\mathrm{p} i}(t)\right)^{\frac{1}{q_{\mathrm{v}}}}+p_{\mathrm{v}}^{\frac{1}{q_{\mathrm{v}}}} x_{\mathrm{p} i}(\Delta t)\right)^{q_{\mathrm{v}}} . $ | (6) |
为适用于核电站等复杂地形场景,SPUFF扩散模型具备了烟团分裂功能。当初始烟团的水平扩散参数σh-in超过设定的阈值σh-max后,烟团将会分裂为5个新烟团(见图 1)[16, 18]。分裂生成的新烟团将满足以下条件:
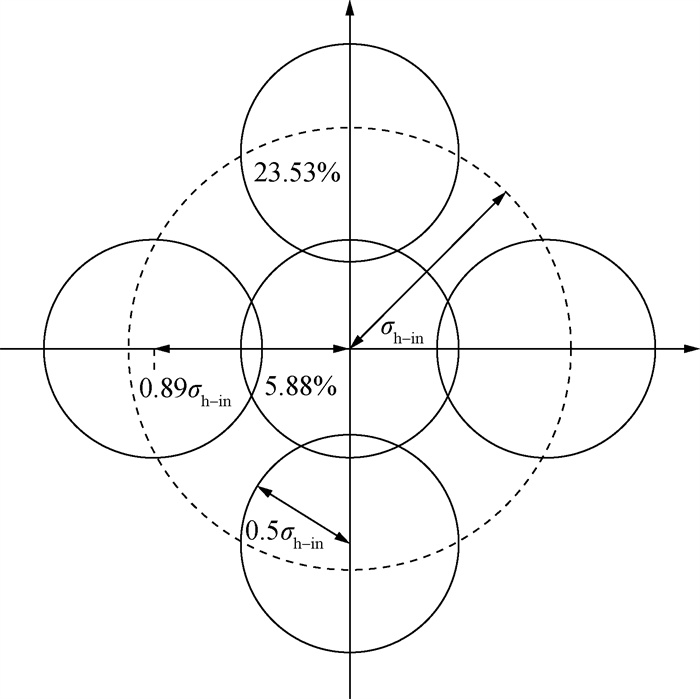
|
| 图 1 SPUFF扩散模型的烟团分裂模式 |
1) 新烟团的水平扩散参数为0.5σh-in;
2) 环绕烟团与中心烟团的质心距离为0.89σh-in;
3) 新烟团与初始烟团在初始烟团的中心处的空气活度浓度或空气质量浓度一致且满足质量守恒,即:中心烟团的质量为初始烟团的5.88%,环绕烟团的质量为初始烟团的23.53%。
SPUFF扩散模型通过对周围烟团的空气活度浓度或空气质量浓度贡献求和来计算网格点(x, y, z)的空气活度浓度或空气质量浓度,均以C(x, y, z)(Bq/m3或g/m3)表示。
| $ \begin{gathered} C(x, y, z)=\sum\limits_{i=1}^N \frac{Q(i) \Delta T}{(2 \pi)^{\frac{3}{2}} \sigma_{\mathrm{h}}^2(i) \sigma_{\mathrm{v}}(i)} \cdot \\ \exp \left(-\frac{1}{2}\left(\frac{\left(x-x_{\mathrm{c}}(i)\right)^2}{\sigma_{\mathrm{h}}^2(i)}+\frac{\left(y-y_{\mathrm{c}}(i)\right)^2}{\sigma_{\mathrm{h}}^2(i)}\right)\right) \cdot \\ {\left[\exp \left(-\frac{1}{2} \frac{\left(z-z_{\mathrm{c}}(i)\right)^2}{\sigma_{\mathrm{v}}^2(i)}\right)+\exp \left(-\frac{1}{2} \frac{\left(z+z_{\mathrm{c}}(i)\right)^2}{\sigma_{\mathrm{v}}^2(i)}\right)+\right.} \\ \left.\exp \left(-\frac{1}{2} \frac{\left(2 z_{\mathrm{inv}}-z_{\mathrm{c}}(i)\right)^2}{\sigma_{\mathrm{v}}^2(i)}\right)\right] \end{gathered} $ | (7) |
其中:N为释放烟团的总个数;Q(i)为第i个烟团的释放率,Bq/s或g/s;ΔT为烟团释放的时间间隔,s;(xc, yc, zc)为第i个烟团的中心坐标,m;σh(i)和σv(i)分别为第i个烟团水平和垂直扩散参数,m;zinv为混合高度,m。
SPUFF扩散模型针对气体考虑干沉积效应,针对气溶胶则考虑干湿沉积效应[11]。其中,气体的干沉积计算参考了文[29]。气溶胶的干、湿沉积计算分别参考了文[29]和[30]。
采用统计参数评估SPUFF扩散模型的有效性,包括:比例偏差(fractional mean bias,FB)、标准化均方误差(normalized mean-square error,NMSE)、几何平均偏差(geometric mean bias,MG)、标准化绝对差(normalized absolute difference,NAD)、模拟值在测量值2、5、10倍以内的比例(FAC2、FAC5、FAC10)。上述指标具体计算公式详见Hanna等[31-32]的研究。Hanna等[32]也对部分关键统计指标提出了接受标准,如表 1所示;同时考虑到场地因素,Hanna指出接受标准满足一半或以上即可认定大气扩散模型的性能足够优秀[32]。
1.2 扩散数据获取
假设以中国三门核电站和日本福岛第一核电站局地尺度范围作为扩散场景,进行气态放射性核素扩散模拟研究。
三门核电站三面环海,依山而建,站内包含6座核反应堆以及若干辅助设施,存在复杂地形和不规则建筑布局[21-23, 33-34]。本文通过风洞实验获取扩散数据,详见1.2.1节。
福岛第一核电站在局地尺度范围内包含了复杂的山区和海洋(太平洋)区域[3, 6],其气象和扩散数据来源详见1.2.2节。
1.2.1 三门核电站场景风洞实验在中国辐射防护研究院的中性大气风洞中开展。在风洞实验中,采用了东(E)和东北(NE)2个方向比例为1∶2 000的扩散界面模型[21-23, 33-34]。风洞实验的气象输入使用了三门核电站气象铁塔于2010—2011年实测的数据(数据委托中国辐射防护研究院提供),包含年平均风速以及风廓线数据。风洞入口的风速约为3.8 m/s。风洞实验选取了CO作为示踪气体,假设其释放位置位于3号反应堆附近。其中,CO采用近地面释放模式释放,在风洞中的释放速度为0.81 m/s。
在E方向和NE方向这2个下风向处,分别布置了249和244个地面红外气体测点,如图 2所示。同时,部分测点被划分为了建筑区(E方向:88个测点;NE:88个测点)、山区(E方向:126个测点;NE方向:120个测点)。当CO释放后,对测点进行采样并依据式(8)计算得CO的扩散因子χ(单位:s/m3)以表示测量数据。
| $ \chi=\frac{C_{\mathrm{b}} U_{\infty}}{Q_{\mathrm{g}} U_{\mathrm{p}}\left(\frac{L_{\mathrm{p}}}{L_{\mathrm{m}}}\right)^2}. $ | (8) |
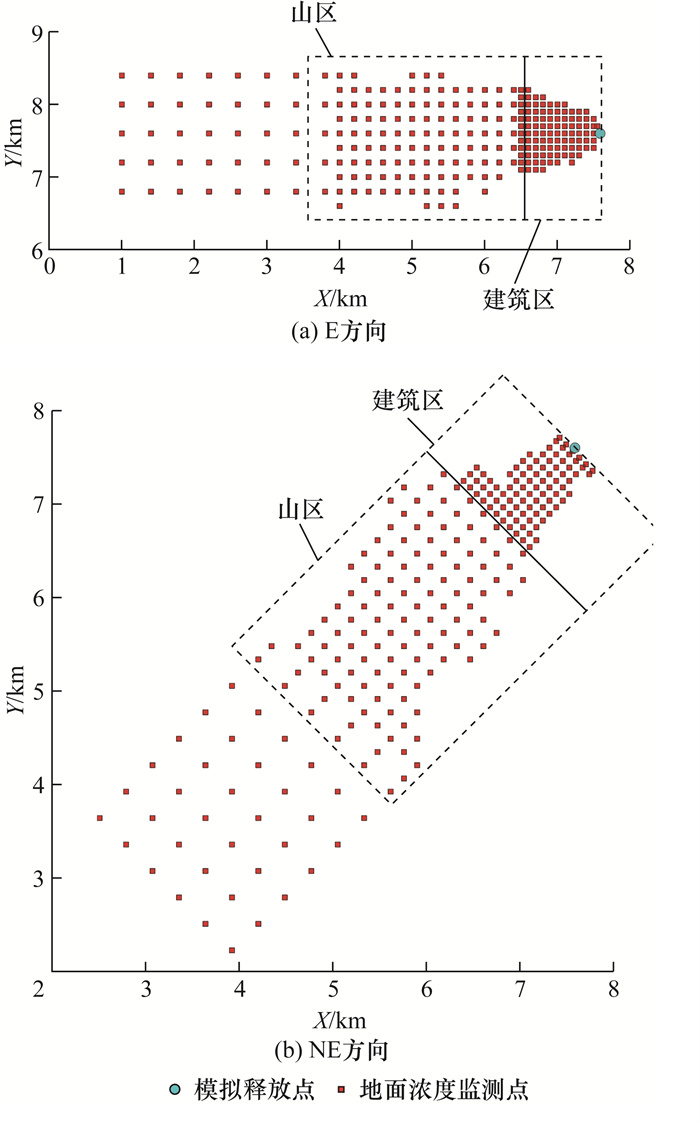
|
| 图 2 风洞实验地面测点布置(假设以三门核电站为扩散场景) |
其中:Cb为经本底值修正的体积浓度,1×10-6;U∞为风洞中模拟排放高度处的环境风速,m/s;Up为现场排放高度处的环境风速,m/s;Qg为示踪气体的体积排放率,m3/s;Lp/Lm为模型的几何缩比。
1.2.2 福岛第一核电站场景以福岛第一核电站内3个地面气象监测点(正门、MP4、MP8)的监测数据[35]作为CALMET模型的输入。高空气象数据采用幂律法插值地面气象监测数据获得[3, 6]。
| $ \frac{U_{\mathrm{h}}}{U_{\mathrm{s}}}=\left(\frac{Z_{\mathrm{h}}}{Z_{\mathrm{s}}}\right)^p . $ | (9) |
其中:Us和Uh分别为地面层高度Zs和高度Zh(单位:m)处的风速,m/s;p为常数,在陆地的取值为0.143。
使用日本遥感技术中心2018年发布的双葉町监测站(福岛第一核电站西北部)所监测的放射性核素137Cs的空气活度浓度[36]来评估SPUFF扩散模型的有效性。文[36]中该核素空气活度浓度由锗半导体探测器(探测限:0.1~0.4 Bq/m3)进行测量,并进行了放射性衰变校正以及交叉污染认定,137Cs的监测时间从日本标准时间2011年3月12日00∶00持续至3月26日00∶00。
1.3 模型参数设定本文使用6.5.0版本的CALMET模型。
针对三门核电站场景,风场以及扩散场的计算域均设为15.2 km×15.2 km的正方形区域,网格尺寸设为100 m。CALMET模型输入的地形和土地类型数据来自中国科学院计算机网络信息中心地理空间数据云平台[37]和欧洲航天局[38]。同时,将核电站内建筑考虑为地形[21, 23]。CO释放率在模拟中设为1×1018 g/s,释放高度为10 m。扩散模拟时间定为烟羽达到稳定状态后的2 h,模型输出时间步长设为1 h。释放源项类型为点源。烟团释放个数设为1个/min并考虑CO气体的干沉积效应。此外,对CO的空气质量浓度进行归一化处理用于测量值与模拟值的对比,具体计算方法为CO空气质量浓度除以释放率。该场景下的σh-max首先由敏感性分析(研究范围:300,500,700,900,1 100,1 300,1 500 m以及关闭分裂模块)得到,最终确定为700 m。
针对福岛第一核电站场景,参见文[6-7],假设以第1—3号机组中心为释放点。风场以及扩散场的计算域均设为40 km × 40 km的正方形区域,网格尺寸设为200 m。扩散模拟时间从日本标准时间2011年3月12日00∶00持续至3月26日00∶00,模型输出时间步长设为1 h。在该场景中,没有考虑建筑区对风场的影响。源项采用广泛应用的Katata反演137Cs源[39]。其中,释放类型考虑为点源,释放高度分别设为20,50,70,120,150 m,源项释放率时间分辨率为0.5 h。此外,烟团释放个数设为1个/min并考虑了137Cs气溶胶干湿沉积效应。福岛核电站场景的σh-max同样首先由敏感性分析(研究范围同上)得到,最终确定为900 m。
2 结果与讨论 2.1 模型性能验证 2.1.1 局地尺度扩散模拟效果SPUFF扩散模型在E和NE这2个方向上局地尺度的扩散结果如图 3a和3c所示,图 3b和3d则对应2个方向上在建筑区内的扩散结果。由图可知,在E方向共248个测点被烟羽有效覆盖,覆盖率达99.60%,这表明了SPUFF扩散模型在横风向的扩散程度良好。SPUFF扩散模型的模拟值与风洞实验测量值保持了较高的一致性,尤其是中部测点(图 3a中红色箭头)、建筑区测点(图 3b中黑色箭头)和释放点附近测点(图 3b中蓝色箭头)。在NE方向,SPUFF扩散模型对测点的覆盖能力同样十分优异,覆盖率达97.54%,在中部、尾部的测点(图 3c中红色箭头)以及建筑区测点(图 3d中黑色箭头)取得了优异的模拟值。同时,SPUFF扩散模型在建筑区较高范围内的模拟值与风洞实验测量值均具有良好的一致性。
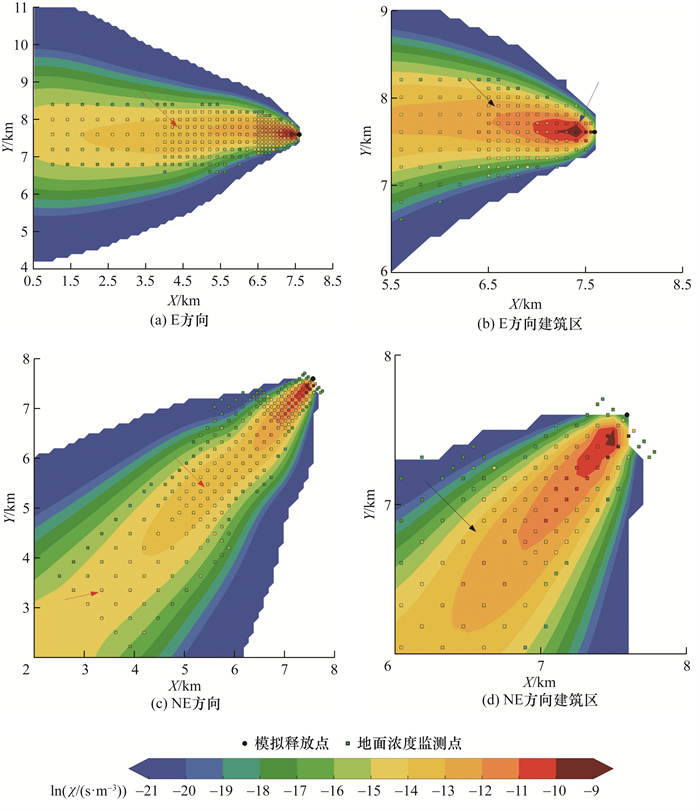
|
| 图 3 SPUFF扩散模型烟羽分布与风洞实验测量值的对比(χ为CD的扩散因子,单位:s/m3) |
与RIMPUFF模型在本场景中的验证结果[21-23]相似的是,受限于烟团模型的扩散机理,SPUFF扩散模型模拟出的烟羽范围会比实际测量范围结果略偏大,这导致部分边缘测点的模拟值与测量值之间存在一定的偏差。
基于E和NE这2个方向上有效覆盖测点处针对SPUFF扩散模型的模拟值与风洞实验的测量值,计算二者的比值,结果如图 4所示,比值越接近1代表SPUFF扩散模型的精确度越高。由图可知,大多数测点对应的比值位于0.5~3,山区边界测点的比值位于0.5~1.5(图 4中红色箭头),体现出了SPUFF扩散模型对该地区的精确模拟。表 2列出了2个方向的相关统计参数,由表可知,4个关键统计指标(FAC2、FB、NMSE、NAD)均满足接受标准(见表 1),E方向上不同分区的FAC2均超过了0.5,NMSE在山区仅为0.2;NE方向上FB在山区达到了0.09。这些结果均表明了SPUFF扩散模型优异的模拟性能。
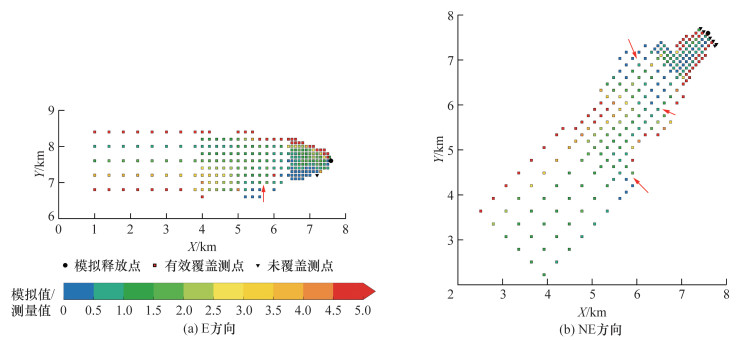
|
| 图 4 SPUFF扩散模型烟羽分布在测点的模拟值与风洞实验测量值对比 |
| E方向 | NE方向 | |||||||
| 统计指标 | 整个区域 | 建筑区 | 山区 | 统计指标 | 整个区域 | 建筑区 | 山区 | |
| FAC2 | 0.52 | 0.51 | 0.57 | FAC2 | 0.48 | 0.40 | 0.48 | |
| FAC5 | 0.77 | 0.72 | 0.83 | FAC5 | 0.76 | 0.66 | 0.82 | |
| FAC10 | 0.88 | 0.86 | 0.89 | FAC10 | 0.87 | 0.80 | 0.90 | |
| FB | -0.17 | -0.18 | -0.10 | FB | 0.37 | 0.43 | 0.09 | |
| NMSE | 0.75 | 0.76 | 0.20 | NMSE | 1.28 | 1.30 | 0.53 | |
| NAD | 0.31 | 0.33 | 0.22 | NAD | 0.39 | 0.40 | 0.30 | |
2.1.2 敏感性分析
SPUFF扩散模型在E和NE方向上采用不同σh-max的局地尺度扩散结果分别如图 5和6所示。σh-max的大小会显著影响烟团模型烟羽的扩散范围,即较小的分裂阈值(σh-max为300 m)会导致烟团显著分裂并制约烟团在横风向的扩散,使得烟羽中心的模拟值明显增高且高于测量值(见图 5a和6a中黑色箭头)。当σh-max达到500 m后,烟团在烟羽中段发生了明显的分裂现象(见图 5b和图 6b中红色箭头),使得烟羽尾部烟团扩散不充分,导致烟羽在尾部测点出现明显的高估。当σh-max为700 m及以上时,烟羽扩散趋势基本稳定,且中心处的高估被有效削弱。此外,σh-max为700 m及以上的扩散结果与不分裂模式基本一致。
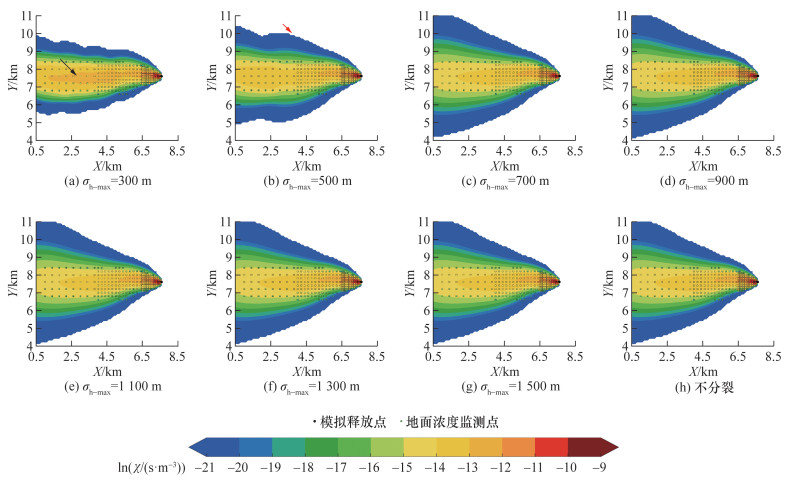
|
| 图 5 E方向上不同分裂阈值模式下烟羽分布的SPUFF扩散模型模拟值与风洞实验测量值对比(χ为CO的扩散因子, 单位:s/m3) |
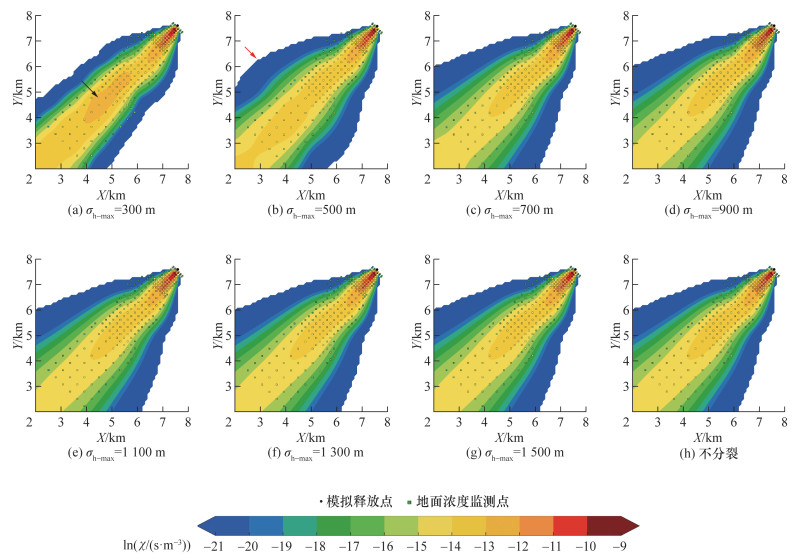
|
| 图 6 NE方向上不同分裂阈值模式下烟羽分布的SPUFF扩散模型模拟值与风洞实验测量值对比(χ为CO的扩散因子, 单位:s/m3) |
由统计评估结果(见图 7)可知,σh-max为700 m及以上,以及不分裂模式下的统计指标(FAC2、FAC5、FAC10、FB、NMSE以及NAD)保持了一致。相比于σh-max为300和500 m时,除NE方向的FB,σh-max为700 m及以上均有效提升了其他统计指标;尤其是FAC2,σh-max为700 m及以上比其为300 m时,在E方向上提升了23.81%,在NE方向上提升45.45%。上述结果表明,在单一气象条件(例如恒定风场)下,应采用σh-max为700 m及以上的烟团分裂模式或者不分裂模式。
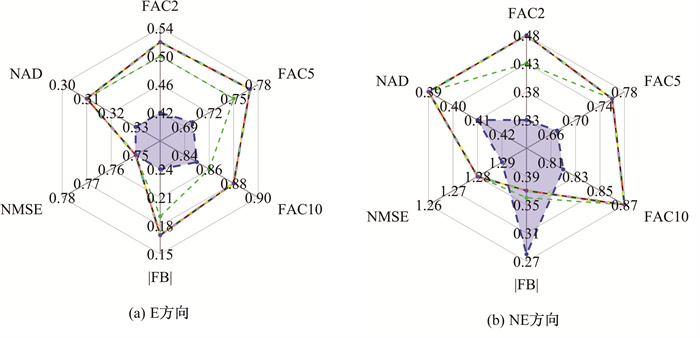
|
| 图 7 敏感性分析结果 |
2.2 模型实用性评估 2.2.1 应用效果分析
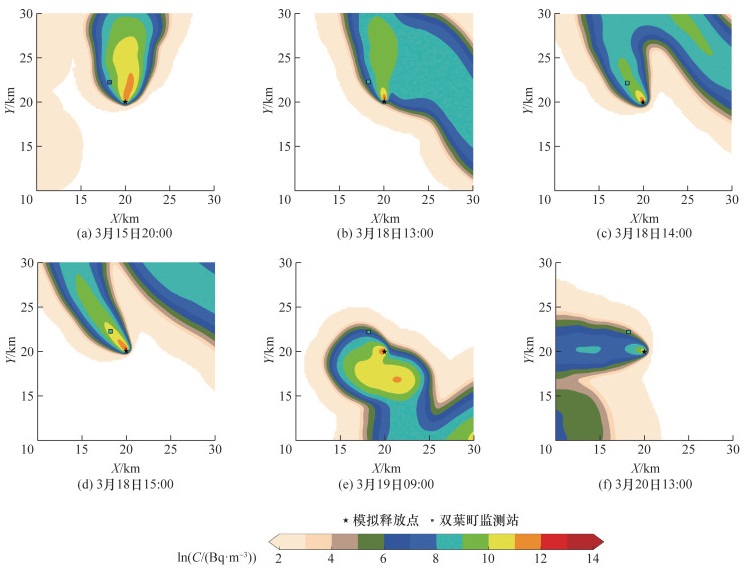
SPUFF扩散模型基于1.2.2节中双葉町监测站137Cs的实际监测值的模拟结果如图 8所示。由图可知,大于100 Bq/m3的监测峰值得到了一定程度的再现。其中,SPUFF扩散模型准确展现了一些反应堆事件[6, 39]引起的监测值的变化,在2011年3月15日20∶00、3月18日13∶00—15∶00、3月19日09∶00以及3月20日13∶00出现较为显著的监测峰(见图中绿色圆圈);在其中4个峰值处(3月15日20∶00、3月18日13∶00、14∶00以及3月19日09∶00)模拟值与监测值的比值分别为3.46、0.29、2.36以及0.29,取得了较好的模拟结果,然而,SPUFF扩散模型也在部分监测峰上出现了较明显的偏差(见图中紫红色箭头),且在低监测值区间的模拟效果不太理想。这可能是因为源项和风场与实际情况存在不可避免的差异。其中Katata源项已被证实在一些时刻的释放率估计存在过高或不足的问题[6],从而影响了SPUFF扩散模型的模拟结果。此外,该场景下的风向偏差尤其制约了扩散模拟结果同低监测值区间在时序上的匹配程度[6]。
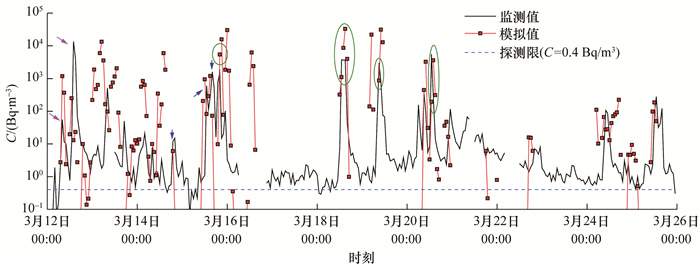
|
| 图 8 137Cs的空气活度浓度监测值与SPUFF扩散模型模拟值的对比(2011年) |
3月15日20∶00、3月18日13∶00—15∶00、3月19日09∶00以及3月20日13∶00峰值时刻的烟羽扩散结果如图 9所示,进一步证实了风场导致烟羽扩散朝向与实际扩散存在偏差。然而,烟团模型的扩散机理(烟羽扩散范围较广)能够在一定程度上弥补由于风场误差导致的扩散偏差,使模型能够较准确地模拟出更多贴合实际的扩散情况。
|
| 注:C为空气活度浓度,单位为Bq/m3。 图 9 SPUFF扩散模型在反应堆事件所致监测峰值期间模拟的烟羽分布(2011年) |
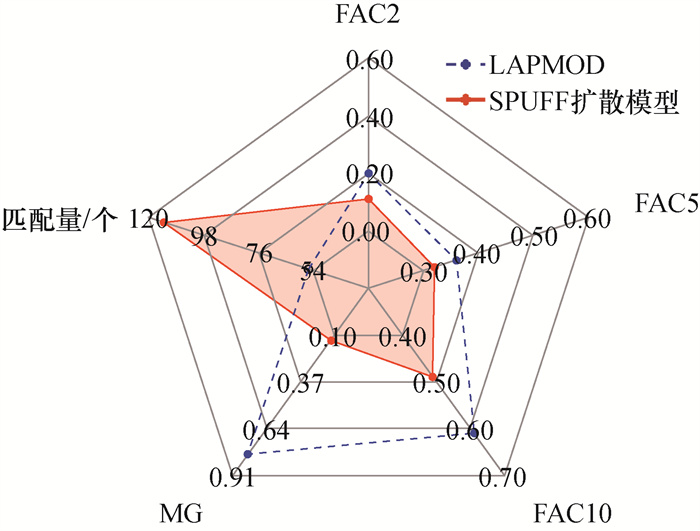
与已有文献中Lagrange粒子模型(LAPMOD)在福岛第一核电站局地尺度扩散的应用研究[6]相比,SPUFF扩散模型表现出一定优势,其在时序上与监测值匹配的模拟值的数量(该评价指标以下简称为“匹配量”)为LAPMOD的2.04倍。例如,SPUFF扩散模型额外再现了3月14日19∶00、3月15日13∶00以及3月15日16∶00等时刻的峰值(图 8中蓝色箭头)。然而,SPUFF扩散模型的FAC2和MG只为LAPMOD的55%以及16.46%(见图 10),表明SPUFF扩散模型对监测值的模拟精度与LAPMOD相比存在一定的不足。
|
| 图 10 SPUFF扩散模型与LAPMOD的模拟指标对比 |
2.2.2 敏感性分析
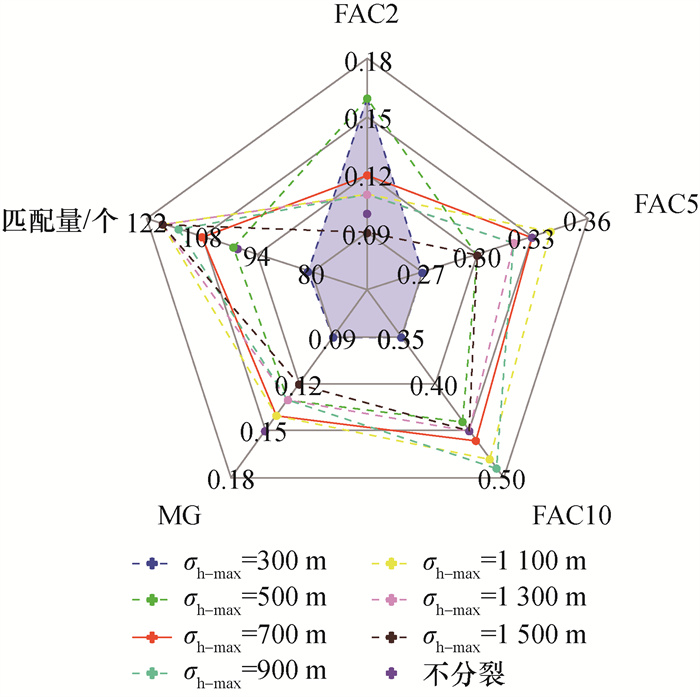
SPUFF扩散模型采用不同σh-max的统计评估结果如图 11所示。σh-max为300 m时SPUFF扩散模型的匹配量最低,仅有81个,推测其原因是较小的σh-max显著促进了烟团分裂,使得烟团模型在烟团数量上趋近于粒子模型概念。由于分裂过后的小尺寸烟团在横风方向的扩张程度不足,致使烟团在横风向的扩散范围被严重限制。随着σh-max的增加,SPUFF扩散模型的匹配量开始升高。当σh-max超过700 m时,匹配量的变化趋于平缓。
|
| 图 11 不同分裂阈值模式下SPUFF扩散模型的模拟指标对比 |
尽管采用不分裂模式得出的MG略高于σh-max为700、900和1 100 m时的情况,但FAC2仅为0.1,是所有模式下的次最低值,且在其余统计指标上也并不表现出优势;同时不分裂模式下SPUFF扩散模型的匹配量低于σh-max为500~1 500 m时的。此外,当σh-max为1 300和1 500 m时,模型的FAC2、FAC5、FAC10和MG不超过σh-max为700、900和1 100 m时的。上述结果表明,在气象多变的复杂地形场景下,烟团分裂十分必要,建议采用分裂阈值范围为700~1 100 m。
3 结论本文利用CALMET模型驱动Lagrange分裂烟团(SPUFF)扩散模型,开展了局地尺度的气态放射性核素扩散模拟研究。假设以三门核电站作为扩散场景开展风洞实验对开发的模型进行了验证,并基于福岛第一核电站附近双葉町监测站的监测数据评估了模型的实用性。同时,针对烟团水平分裂阈值开展了敏感性分析。
SPUFF扩散模型针对三门核电站模拟场景中的东风和东北风向上的扩散情况取得了优异的模拟效果,扩散烟羽覆盖了绝大多数的测点,覆盖率分别为99.60%和97.54%,模拟值满足模型接受标准的4个关键统计指标(FAC2、FB、NMSE以及NAD),表明该模型可适用于复杂地形核电站的场景模拟。同时,SPUFF扩散模型成功复现了福岛第一核电站附近双葉町监测站137Cs空气活度浓度监测值在一定时段内的变化情况和峰值现象,该结果较LAPMOD具有的优势是模拟值可在时序上匹配更多数量的监测值。
在单一气象(恒定风场)条件下,烟团可采用不分裂模式;在气象多变、地形复杂条件下,有必要使用分裂模式。本文建议在局地尺度下采用的分裂阈值范围为700~1 100 m。由于不同核电站所处地形及气象条件的差异,后续建议结合具体的气象条件以及地形条件进一步研究烟团模型的分裂策略。
| [1] |
LE N B T, KORSAKISSOK I, MALLET V, et al. Uncertainty study on atmospheric dispersion simulations using meteorological ensembles with a Monte Carlo approach, applied to the Fukushima nuclear accident[J]. Atmospheric Environment: X, 2021, 10: 100112. DOI:10.1016/j.aeaoa.2021.100112 |
| [2] |
LI X P, SONG J Y, YANG L, et al. Source term inversion coupling kernel principal component analysis, whale optimization algorithm, and backpropagation neural networks (KPCA- WOA-BPNN) for complex dispersion scenarios[J]. Progress in Nuclear Energy, 2024, 171: 105171. DOI:10.1016/j.pnucene.2024.105171 |
| [3] |
ZHUANG S H, FANG S, DONG X W, et al. Local atmospheric transport behaviors of representative radionuclides during the Fukushima accident: A 200-m-resolution cross-scale study from site to 20 km[J]. Journal of Environmental Radioactivity, 2023, 265: 107212. DOI:10.1016/j.jenvrad.2023.107212 |
| [4] |
SONG J Y, YANG L, LI H T, et al. Comparison of intelligent optimization algorithms in neural network model for nuclear accident source term evaluation[C]//Proceedings of the ASME 2023 International Conference on Environmental Remediation and Radioactive Waste Management. Stuttgart, Germany: American Society of Mechanical Engineers, 2023.
|
| [5] |
TERADA H, NAGAI H, TANAKA A, et al. Atmospheric-dispersion database system that can immediately provide calculation results for various source term and meteorological conditions[J]. Journal of Nuclear Science and Technology, 2020, 57(6): 745-754. DOI:10.1080/00223131.2019.1709994 |
| [6] |
YANG L, FANG S, ZHUANG S H, et al. Atmospheric 137Cs dispersion following the Fukushima Daiichi nuclear accident: Local-scale simulations using CALMET and LAPMOD[J]. Annals of Nuclear Energy, 2024, 195: 110137. DOI:10.1016/j.anucene.2023.110137 |
| [7] |
杨力, 王存友, 陈义学, 等. 四种拉格朗日粒子浓度计算方法的评估——箱式计数法、高斯核、均匀核和抛物线核[J]. 中国环境科学, 2023, 43(7): 3404-3415. YANG L, WANG C Y, CHEN Y X, et al. Evaluation of four Lagrangian particle concentration calculation methods-box counting, Gaussian kernel, uniform kernel and parabolic kernel[J]. China Environmental Science, 2023, 43(7): 3404-3415. (in Chinese) |
| [8] |
SEKIYAMA T T, KAJINO M. Performance of a 250-m grid eulerian dispersion simulation evaluated at two coastal monitoring stations in the vicinity of the Fukushima Daiichi nuclear power plant[J]. Journal of the Meteorological Society of Japan. Ser. Ⅱ, 2021, 99(4): 1089-1098. DOI:10.2151/jmsj.2021-052 |
| [9] |
刘爱华, 蒯琳萍. 放射性核素大气弥散模式研究综述[J]. 气象与环境学报, 2011, 27(4): 59-65. LIU A H, KUAI L P. A review on radionuclides atmospheric dispersion modes[J]. Journal of Meteorology and Environment, 2011, 27(4): 59-65. (in Chinese) |
| [10] |
BARBERO D, RIBSTEIN B, NIBART M, et al. Reduction of simulation times by application of a kernel method in a high-resolution Lagrangian particle dispersion model[J]. Air Quality, Atmosphere & Health, 2023, 1-13. |
| [11] |
BELLASIO R, BIANCONI R, MOSCA S, et al. Formulation of the Lagrangian particle model (LAPMOD) and its evaluation against Kincaid SF6 and SO2 datasets[J]. Atmospheric Environment, 2017, 163: 87-98. DOI:10.1016/j.atmosenv.2017.05.039 |
| [12] |
BELLASIO R, BIANCONI R, MOSCA S, et al. Incorporation of numerical plume rise algorithms in the Lagrangian particle model (LAPMOD) and validation against the Indianapolis and Kincaid datasets[J]. Atmosphere, 2018, 9(10): 404. DOI:10.3390/atmos9100404 |
| [13] |
UL HAQ A, NADEEM Q, FAROOQ A, et al. Assessment of Lagrangian particle dispersion model (LAPMOD) through short range field tracer test in complex terrain[J]. Journal of environmental radioactivity, 2019, 205-206: 34-41. DOI:10.1016/j.jenvrad.2019.04.015 |
| [14] |
LEELÖSSY Á, LAGZI I, KOVÁCS A, et al. A review of numerical models to predict the atmospheric dispersion of radionuclides[J]. Journal of Environmental Radioactivity, 2018, 182: 20-33. DOI:10.1016/j.jenvrad.2017.11.009 |
| [15] |
VAN LEUKEN J P G, SWART A N, HAVELAAR A H, et al. Atmospheric dispersion modelling of bioaerosols that are pathogenic to humans and livestock: A review to inform risk assessment studies[J]. Microbial Risk Analysis, 2016, 1: 19-39. DOI:10.1016/j.mran.2015.07.002 |
| [16] |
郝琦. 基于MPI并行计算框架的核事故后果评价系统研发[D]. 北京: 华北电力大学(北京), 2022. HAO Q. Research and development of nuclear accident consequence evaluation system based on MPI parallel computing framework[D]. Beijing: North China Electric Power University (Beijing), 2022. (in Chinese) |
| [17] |
樊庆旭. 基于拉格朗日烟团模型的放射性核素扩散模拟研究[D]. 北京: 华北电力大学(北京), 2023. FAN Q X. Research on simulation of radionuclide dispersion based on Lagrange puff model[D]. Beijing: North China Electric Power University (Beijing), 2023. (in Chinese) |
| [18] |
THYKIER-NIELSEN S, DEME S, MIKKELSEN T K. Description of the atmospheric dispersion module RIMPUFF: RODOS(WG2)-TN(98)-02[R]. Riso National Laboratory, PO Box, 1999, 49.
|
| [19] |
SCIRE J S, STRIMAITIS D G, YAMARTINO R J. A user's guide for the CALPUFF dispersion model[M]. 5th ed. Concord: Earth Tech, Inc., 2000.
|
| [20] |
刘毅, 刘龙, 李王锋, 等. 石化园区规划大气环境风险模拟方法与案例[J]. 清华大学学报(自然科学版), 2015, 55(1): 80-86. LIU Y, LIU L, LI W F, et al. Modeling regional atmospheric risks of petrochemical park planning[J]. Journal of Tsinghua University (Science and Technology), 2015, 55(1): 80-86. (in Chinese) |
| [21] |
DONG X W, ZHUANG S H, FANG S, et al. Multi-scenario validation of CALMET-RIMPUFF for local-scale atmospheric dispersion modeling around a nuclear powerplant site with complex topography[J]. Journal of Environmental Radioactivity, 2021, 229-230: 106547. DOI:10.1016/j.jenvrad.2021.106547 |
| [22] |
DONG X W, ZHUANG S H, FANG S, et al. Site-targeted evaluation of SWIFT-RIMPUFF for local-scale air dispersion modeling around Sanmen nuclear power plant based on multi-scenario wind tunnel experiments[J]. Annals of Nuclear Energy, 2021, 164: 108593. DOI:10.1016/j.anucene.2021.108593 |
| [23] |
LIU Y, LI H, SUN S D, et al. Enhanced air dispersion modelling at a typical Chinese nuclear power plant site: Coupling RIMPUFF with two advanced diagnostic wind models[J]. Journal of Environmental Radioactivity, 2017, 175-176: 94-104. DOI:10.1016/j.jenvrad.2017.04.016 |
| [24] |
SCIRE J S, ROBE F R, FERNAU M E, et al. A user's guide for the CALMET meteorological model[M]. 5th ed. Concord: Earth Tech, 2000.
|
| [25] |
YANG L, SONG J Y, CHEN Y X, et al. Evaluation of multiple Lagrangian particle dispersion concentration calculation methods based on the Belgian field experiment: Coupling CALMET with LAPMOD[C]//Proceedings of the 30th International Conference on Nuclear Engineering (ICONE). Kyoto, Japan: The Japan Society of Mechanical Engineers, 2023: 1158.
|
| [26] |
JANICKE U, JANICKE L. A three-dimensional plume rise model for dry and wet plumes[J]. Atmospheric Environ- ment, 2001, 35(5): 877-890. DOI:10.1016/S1352-2310(00)00372-1 |
| [27] |
WEBSTER H N, THOMSON D J. Validation of a Lagrangian model plume rise scheme using the Kincaid data set[J]. Atmospheric Environment, 2002, 36(32): 5031-5042. DOI:10.1016/S1352-2310(02)00559-9 |
| [28] |
国家技术监督局, 国家环境保护局. 制定地方大气污染物排放标准的技术方法: GB/T 3840—1991[S]. 北京: 中国标准出版社, 1991. The State Bureau of Quality and Technical Supervision, State Environmental Protection Administration. Technical methods for making local emission standards of air pollutants: GB/T 3840—1991[S]. Beijing: Standards Press of China, 1991. (in Chinese) |
| [29] |
BAKLANOV A, SØRENSEN J H. Parameterisation of radionuclide deposition in atmospheric long-range transport modelling[J]. Physics and Chemistry of the Earth, Part B: Hydrology, Oceans and Atmosphere, 2001, 26(10): 787-799. DOI:10.1016/S1464-1909(01)00087-9 |
| [30] |
ZHANG L M, GONG S L, PADRO J, et al. A size-segregated particle dry deposition scheme for an atmospheric aerosol module[J]. Atmospheric Environment, 2001, 35(3): 549-560. DOI:10.1016/S1352-2310(00)00326-5 |
| [31] |
HANNA S R, HANSEN O R, DHARMAVARAM S. FLACS CFD air quality model performance evaluation with Kit Fox, MUST, Prairie Grass, and EMU observations[J]. Atmospheric Environment, 2004, 38(28): 4675-4687. DOI:10.1016/j.atmosenv.2004.05.041 |
| [32] |
HANNA S, CHANG J. Acceptance criteria for urban dispersion model evaluation[J]. Meteorology and Atmospheric Physics, 2012, 116(3-4): 133-146. |
| [33] |
WANG S T, LI X P, FANG S, et al. Validation and sensitivity study of Micro-SWIFT SPRAY against wind tunnel experiments for air dispersion modeling with both heterogeneous topography and complex building layouts[J]. Journal of Environmental Radioactivity, 2020, 222: 106341. |
| [34] |
刘蕴, 方晟, 李红, 等. 基于四维变分资料同化的核事故源项反演[J]. 清华大学学报(自然科学版), 2015, 55(1): 98-104. LIU Y, FANG S, LI H, et al. Source inversion in nuclear accidents based on 4D variational data assimilation[J]. Journal of Tsinghua University (Science and Technology), 2015, 55(1): 98-104. (in Chinese) |
| [35] |
TOKYO ELECTRIC POWER COMPANY. On-site meteorological data from Fukushima Daiichi nuclear power plant[EB/OL]. (2012)[2024-02-13]. https://www.tepco.co.jp/decommission/data/monitoring/monitoring_post/index-j.html.
|
| [36] |
TSURUTA H, OURA Y, EBIHARA M, et al. Time-series analysis of atmospheric radiocesium at two SPM monitoring sites near the Fukushima Daiichi nuclear power plant just after the Fukushima accident on March 11, 2011[J]. Geochemical Journal, 2018, 52(2): 103-121. |
| [37] |
GEOSPATIAL DATA CLOUD SITE, COMPUTER NETWORK INFORMATION CENTER, CHINESE ACADEMY OF SCIENCES. Terrain data[EB/OL]. (2015)[2024-02-13]. http://www.gscloud.cn/sources/details/421?pid=302.
|
| [38] |
EUROPEAN SPACE AGENCY (ESA). GlobCover land cover maps[EB/OL]. (2009)[2024-02-13]. http://due.esrin.esa.int/page_globcover.php.
|
| [39] |
KATATA G, CHINO M, KOBAYASHI T, et al. Detailed source term estimation of the atmospheric release for the Fukushima Daiichi nuclear power station accident by coupling simulations of an atmospheric dispersion model with an improved deposition scheme and oceanic dispersion model[J]. Atmospheric Chemistry and Physics, 2015, 15(2): 1029-1070. |



