2. 水利部粤港澳大湾区水安全保障重点实验室, 广州 510611;
3. 水利部珠江河口动力学及伴生过程调控重点实验室, 广州 510611;
4. 清华大学 水利水电工程系, 北京 100084
2. Key Laboratory of Water Security Guarantee in Guangdong-Hong Kong-Macao Greater Bay Area of Ministry of Water Resources, Guangzhou 510611, China;
3. Key Laboratory of Pearl River Estuary Regulation and Protection of Ministry of Water Resources, Guangzhou 510611, China;
4. Department of Hydraulic Engineering, Tsinghua University, Beijing 100084, China
中国地处欧亚大陆东亚季风气候区,在全球变暖和城镇化发展的共同影响下,极端降水频发,洪涝灾害形势严峻[1-2]。水动力模型是洪涝灾害防御中的关键科学工具,通过对河道、管网、地表的水流进行数学建模,可量化分析不同因素对城市防洪排涝系统的影响,近年来得到了越来越多的研究和应用[3-5]。其中,二维水动力模型可模拟洪涝在地表的淹没及演进过程,在洪涝预报预警中应用广泛[6-7]。二维水动力模型的计算效率主要受网格数量、时间步长的影响:在精细化洪涝过程模拟中,若网格分辨率提高2倍,网格数量将提高4倍;为保持模型计算稳定,时间步长缩减1/2,最终导致模型整体计算量提高接近一个数量级,模型的计算效率大大降低[8]。为提高模型计算效率,学者们提出了多种模型计算加速方法[9-12]。部分学者通过使用动态网格策略,仅计算有效的网格单元以降低网格数量增多的影响;部分学者则使用局部时间步长技术尽可能降低时间步长减小带来的计算效率损失。但是,现有研究基本仅针对网格数量或时间步长的单一方面进行模型计算加速,能否结合两种算法的优势从两个方面同步加速,以尽可能减少模型计算量、提高模型计算效率,有待进一步研究。
动态网格控制算法最早由Judi等[13]提出,该算法将湿网格单元和相邻干湿网格单元组成有效单元组,仅对有效单元组进行通量计算和变量更新,大幅度减少了模型计算量;进一步结合并行计算技术后,取得了最大310倍加速比的计算加速效果;Hou等[14]则将这一算法引入Godunov格式有限体积法的二维水动力模型中,在案例测试计算中加速超50%。
在城市洪涝模型中,常需通过局部加密技术细化道路、建筑等重点区域的网格。为保证模型计算稳定,传统模型普遍采用最小网格在满足Courant-Friedrichs-Lewy (CFL)稳定性条件下的时间步长进行全局变量更新,称为全局最小时间步长(global time step, GTS)技术。GTS技术使较大网格区域也必须按照最小时间步长进行更新,降低了模型的计算效率。为此,Sanders[15]提出局部时间步长(local time step, LTS)技术,通过将模型更新时选取的全局最小时间步长修改为选取与CFL稳定性条件相适应的分级时间步长,提高了模型的计算效率。但是,当局部时间步长级数取较大值时,Sanders的算法可能导致模型干湿边界处的计算结果发散,Hu等[16]则通过优化干湿边界处网格动态更新策略,进一步提升了局部时间步长技术的稳定性,并将其推广应用至水沙、潮波等研究中[17-18]。
如果能够在有效单元上采用分级时间步长技术,有望进一步减少模型计算量,进而提高模型计算效率。本文通过对自主开发的HydroMPM洪涝模拟模型进行改进,提出了动态网格控制策略与局部时间步长技术相结合的城市洪涝模型加速方法,解决了洪涝模拟模型中无效网格单元多、无效计算量大的问题,大幅减少了模型的计算量,提高了模型计算效率。
1 洪涝模拟模型 1.1 一二维耦合的洪涝模拟模型 1.1.1 一维水动力模型采用Saint-Venant方程组作为一维非恒定流控制方程,包括连续方程和运动方程。
| $ \frac{\partial z}{\partial t}+\frac{1}{B} \frac{\partial Q}{\partial x}=\frac{q}{B}, $ | (1) |
| $ \frac{\partial Q}{\partial t}+g A \frac{\partial z}{\partial x}+\frac{\partial}{\partial x}(\beta \bar{u} Q)+g \frac{|Q| Q}{c^2 A R}=0 . $ | (2) |
式中:x为流距(m);t为时间(s);z为水位(m);B为过水断面水面宽度(m);Q为流量(m3/s);q为侧向单宽流量(m2/s),正值表示流入,负值表示流出;A为过水断面面积(m2);g为重力加速度(m/s2);u为断面平均流速;β为校正系数;R为水力半径(m);c为Chézy系数,c=R1/6/n,n为Manning糙率系数。
数值求解方面,一维河网水动力模型采用单元中心型有限体积法求解控制方程,使用Riemann求解器计算控制体之间的数值通量,通过汊点预测校正法计算河道汊点的内边界条件。上述方法能够很好地保证复杂河网及河道地形条件下一维河网水动力模型求解的稳定性,相关求解方法见文[19],本文不再赘述。一维管网水动力模型使用国内外广泛使用的雨水管理模型(storm water management model,SWMM)得到地下管网中水体流动情况,详见文[20]。
1.1.2 二维水动力模型二维水动力模型采用改进的二维浅水方程作为控制方程,
| $ \frac{\partial \boldsymbol{U}}{\partial t}+\frac{\partial \boldsymbol{E}}{\partial x}+\frac{\partial \boldsymbol{G}}{\partial y}=\boldsymbol{S} . $ | (3) |
其中:
| $ \begin{gathered} \boldsymbol{U}=\left[\begin{array}{c} h \\ h u \\ h v \end{array}\right], \boldsymbol{E}=\left[\begin{array}{c} h u \\ h u^2+\frac{g\left(h^2-b^2\right)}{2} \\ h u v \end{array}\right], \\ \boldsymbol{G}=\left[\begin{array}{c} h v \\ h u v \\ h v^2+\frac{g\left(h^2-b^2\right)}{2} \end{array}\right], \\ \boldsymbol{S}=\left[\begin{array}{c} 0 \\ g(h+b) S_{0 x}-g h S_{f x} \\ g(h+b) S_{0 y}-g h S_{f y} \end{array}\right] . \end{gathered} $ |
式(3)中:U为守恒向量,E和 G分别为x和y方向上的通量向量,S为源项。h为水深;u、v分别为x、y方向的垂向平均流速;b为底高程;S0x和S0y分别为x和y方向上的底坡源项,S0x=-b/x,S0y=-b/y;Sfx和Sfy分别为x和y方向上的摩阻源项,其中Sfx=n2u(u2+v2)1/2h-4/3,Sfy=n2v(u2+v2)1/2h-4/3。
数值求解方面,采用非结构三角网格划分计算域,运用单元中心型有限体积法进行控制方程离散。底高程定义于网格节点,水深、水位和流速等变量定义于单元中心。采用近似Riemann求解Harten-Lax-van Leer-contact (HLLC)计算数值通量,运用具有时空二阶精度的守恒律的单调上游中心格式(monotone upstream-centered schemes for conservation laws,MUSCL)进行方程求解。计算模块主要包括单元干湿状态分类、斜率计算、预测步、空间重构、Riemann问题求解、边界条件处理、源项处理和校正步。数值求解的详细过程可参考文[21]。
1.1.3 模型耦合一维、二维水动力模型通过耦合边界的水力连接条件来实现模型联解。其中一维河网水动力模型与二维水动力模型使用侧向联解的方式耦合,通过构造Riemann问题计算耦合边界的数值通量。与传统基于堰流公式的侧向联解相比,通过Riemann求解可适应复杂形状溃口及无溃口的漫堤洪水的模拟,同时避免了堰流公式中流量系数选取的不确定性,计算精度较高[22]。一维管网水动力模型与二维水动力模型在检查井、雨水箅子中使用改进的垂向流量交换方法计算垂向数值交换通量,该方法通过区分节点超载、未超载等不同水力状态选取不同经验公式计算垂向流量,在保证水量平衡的同时提高了垂向耦合的稳定性[23]。一维河网水动力模型与一维管网水动力模型通过耦合断面处的河道水位进行联解,管网排出水量为河网水动力的源项,河道水位为管网水动力的边界条件。
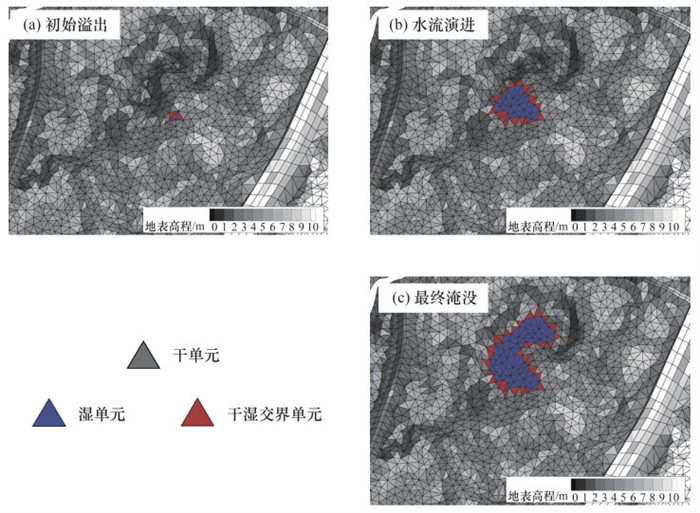
1.2 模型计算加速策略 1.2.1 动态网格控制策略在实际的洪涝淹没过程中,洪水、涝水由溃口或检查井流至地表,受局部地形糙率等影响逐渐向周围扩散。上述过程中,在部分模拟时段或整个模拟时段,湿单元与干湿交界单元组成的有效计算单元组数量要远小于总网格数量。如图 1所示,城市管网因超载而满溢至地表时,计算区域内仅有一个网格是湿单元。为保证地表水流能正常演进,选取湿单元及其周围3个干湿交界单元组成有效单元组,仅对有效单元组网格进行通量计算和单元变量更新,即可得到正确的洪水演进结果(图 1a);受局部地形以及管网涝水持续溢出影响,地表水流持续演进,淹没范围增大,湿单元增多,选取湿单元以及相邻干湿交界单元组成新的有效单元组,可持续进行地表水流演进的计算(图 1b);最终,管网溢出造成局部淹没。整个计算过程中有效单元组网格数量远小于模型总网格数量(图 1c),使用动态网格控制策略可显著减小计算量、提高计算效率[13]。
|
| 图 1 动态网格控制策略网格更新示意图 |
在整个动态网格控制策略中,核心步骤是每一时间步动态更新参与循环计算的网格边、网格单元。首先,根据网格边两侧单元的水深确定网格边是否需要计算,即若网格边为边界边或任意一侧单元的水深大于0 m,则该边为有效计算边,否则该边不参与计算;其次,根据边的计算状态确定单元状态,即若单元的任意一条边为有效计算边,则该单元为有效计算单元,否则该单元不参与计算[13-14]。
1.2.2 局部时间步长技术局部时间步长技术通过分级进行计算和单元更新来减少模型计算量,提高模型计算效率[15-16]。具体步骤主要为:1) 根据CFL稳定性条件,计算每个网格单元的允许最大时间步长Δti,见式(4);2) 获取网格整体最小时间步长Δtmin,见式(5);3) 根据每个网格最大时间步长和整体最小时间步长确定每个网格单元、网格边局部时间步长级数mi*、mfj,见式(6)—(8);4) 根据时间步长级数确定每个网格单元最终的局部时间步长ΔtLTS_i,见式(9);5) 按照局部时间步长和网格对应的局部步长级数进行通量计算和单元更新,当局部时间步长循环完毕时,模型整体上已按Δtmin·2mmax步长更新,其中mmax=max (mi*)为模型的最大加速级数。
| $ \begin{gathered} \Delta t_i=C r \min _{l=1, 2, \cdots, L}\left(\frac{R_{i l}}{\sqrt{u_{i l}^2+v_{i l}^2}+\sqrt{g h_i}}\right), \end{gathered} $ | (4) |
| $ \Delta t_{\min }=\min _{i=1, 2, \cdots, N_{\mathrm{c}}}\left(\Delta t_i\right), $ | (5) |
| $ m_i=\min \left(\operatorname{int}\left(\frac{\ln \left(\Delta t_i / \Delta t_{\min }\right)}{\ln 2}\right), m_{\text {user }}\right), $ | (6) |
| $ m_{\mathrm{f} j}=\min _{j=1, 2, \cdots, N_{\mathrm{f}}}\left(m_{j \mathrm{~L}}, m_{j \mathrm{R}}\right), $ | (7) |
| $ m_i^*=\min \left(m_i, m_{i 1}, m_{i 2}, \cdots, m_{i l}\right), $ | (8) |
| $ \Delta t_{\mathrm{LTS}_{-} i}=2^{m_i^*} \Delta t_{\min } . $ | (9) |
式中:uil和vil为第i个网格单元第l条边的平均流速沿x和y方向上的分量;hi为第i个网格中心处的水深;Cr为Courant数。muser为用户定义的值,用于限制时间步长级数:muser=0为模型采用传统全局最小时间步长算法,此时ΔtLTS_i=Δtmin。mfj为所有网格边中的第j条边的时间步长级数;mjL和mjR分别为第j条边左右两个网格的时间步长级数;mi*为网格的实际局部时间步长级数。ΔtLTS_i为网格的局部时间步长;Nc为网格单元总数,Nf为网格边总数。
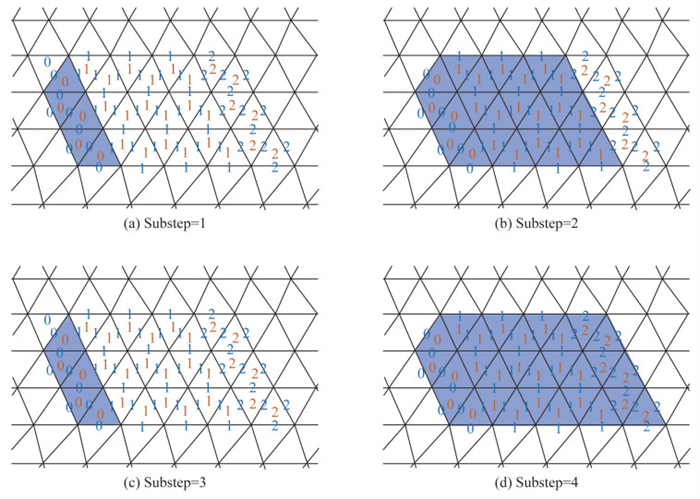
以muser=2为例介绍使用局部时间步长技术的变量更新过程。当mmax=muser=2时,模型整体上按Δtmin·2mmax更新,局部时间步长技术内部小循环总步数为2mmax=4。假设网格边、网格单元的局部时间步长级数如图 2所示,级数为0的网格单元实际更新步长为Δtmin,级数为1的网格单元实际更新步长为2Δtmin,级数为2的网格单元实际更新步长为4Δtmin。因此,当小循环步数(Substep)为1时,实际更新的网格单元级数为0 (图 2a);当小循环步数为2时,实际更新的网格单元级数为0、1 (图 2b);当小循环步数为3时,实际更新的网格单元级数为0 (图 2c);当小循环步数为4时,实际更新的网格单元级数为0、1、2 (图 2d)。至此,所有网格完成了一次同步更新。由于在整个局部时间步长更新流程中,网格单元、边分级参与通量计算和变量更新,相较于传统全局最小时间步长算法,减少了实际参与计算的网格单元、边的数量,因此能够提高模型计算效率。
|
| 图 2 局部时间步长技术网格更新示意图 |
1.2.3 动态网格和局部时间步长融合策略
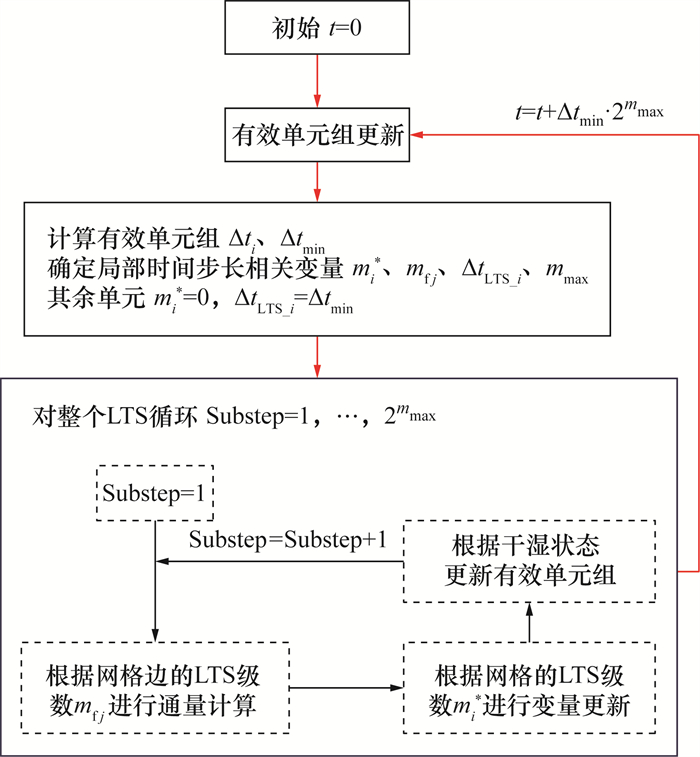
动态网格控制策略基于有效单元组,仅对湿单元及干湿边界单元进行计算,减少了计算量;局部时间步长技术则通过设置不同更新级数,使单元分级更新并最终同步。本文基于前人研究成果,提出了一种动态网格控制策略与局部时间步长技术融合方法,先利用动态网格控制策略确定计算区域内有效单元组,之后再使用局部时间步长技术,根据有效单元组的局部时间步长对模型进行分级更新。融合算法的流程图如图 3所示。
|
| 图 3 动态网格与局部时间步长融合的计算原理示意图 |
2 案例测试 2.1 理想溃坝算例
理想溃坝算例是验证局部时间步长技术的经典算例。算例模拟一个长1 000 m、宽100 m的长方形光滑水槽在120 s内的理想溃坝过程。坝体设置在500 m处,水槽左侧(上游)初始为静水,水深1 m,右侧(下游)为干床面。为体现网格细化对模型效率和算法效率的影响,算例设置3套不同的计算网格:1) 均匀三角形网格(图 4a),网格边长为2 m,网格总数57 812,节点总数29 457;2) 沿坝址局部加密的非均匀三角形网格(图 4b),最小边长1 m,最大2 m,网格总数63 032,节点总数32 067;3) 沿水槽中心线局部加密的非均匀三角形网格(图 4c),最小边长1 m,最大2 m,网格总数114 820,节点总数57 961。

|
| 图 4 理想溃坝算例网格设置 |
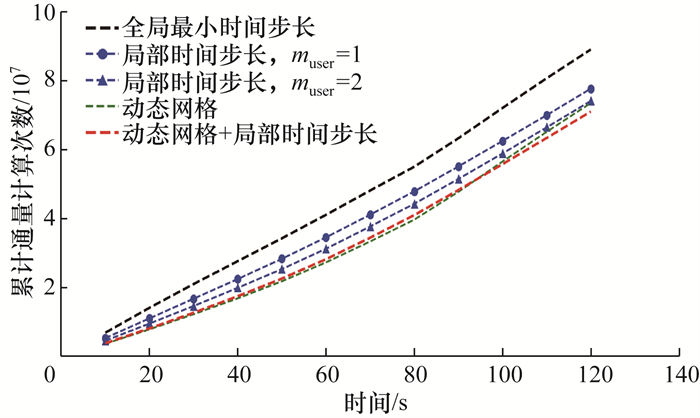
局部时间步长技术和动态网格控制策略均通过减少模型计算量来提高计算效率。图 5以累计通量计算次数(调用Riemann算子计算网格边通量次数)为指标,分析了均匀三角形网格在不同算法条件下模型整体计算量。
|
| 图 5 均匀三角形网格不同加速策略下累计通量计算次数对比 |
图 5中的黑线表示传统全局最小时间步长更新策略下累计通量计算次数随计算时长变化过程。前80 s溃坝波在水槽右侧的干床面演进,均匀网格下累计通量计算次数基本保持线性增长,第80 s时,累计通量计算次数为5.5×107;第80 s后溃坝洪水到达水槽右侧底部,流态发生剧烈变化,形成局部壅水,计算时间步长减小,累计通量计算次数虽依然基本呈线性增长但斜率增大,单位时长累计通量计算次数增大;至120 s时,累计通量计算次数达到8.9×107。
图 5中的两条蓝线分别表示不同局部时间步长加速级数下累计通量计算次数随计算时长变化过程。此条件下,前80 s左侧淹没区不同时间步长下差异不大,依旧以全局最小时间步长更新,右侧干床面时间步长设置不影响模型计算结果,故按照加速级数确定更新步长,第80 s加速级数为1 (muser=1)时累计通量计算次数为4.8×107,加速级数为2 (muser=2)时累计通量计算次数为4.4×107;第80 s后不同时间步长导致的差异加大,但局部时间步长技术依旧能保持大部分网格按照较大步长更新,故单位时长累计通量计算次数较全局最小时间步长方案减少,第120 s加速级数为1 (muser=1)时累计通量计算次数为7.8×107,加速级数为2 (muser=2)时累计通量计算次数为7.4×107。
图 5中的绿线表示动态网格控制策略下累计通量计算次数随计算时长变化过程。动态网格控制策略仅对湿网格及其相邻的干湿边界网格进行更新,不需要考虑其余干网格的情况,故前期其计算效率较其他算法有较大优势,第80 s时累计通量计算次数为4.0×107;第80 s后随着溃坝洪水淹没整个水槽,动态网格控制策略实质上已失效,模型性能与全局最小时间步长算法保持一致,累计通量计算次数快速增加,至第120 s时,累计通量计算次数为7.3×107。
图 5中的红线表示动态网格与局部时间步长融合策略下累计通量计算次数随计算时长变化过程。融合策略仅对有效网格使用局部时间步长技术,故相对于局部时间步长技术,融合策略能进一步减少累计通量计算次数。为保持局部时间步长计算稳定,有效单元中需纳入干湿边界处的更多网格,故前80 s其累计通量计算次数比动态网格控制策略略高,第80 s时累计通量计算次数为4.1×107;第80 s后溃坝洪水淹没整个水槽,动态网格控制策略失效,融合算法可借助局部时间步长技术减少累计通量计算次数,至第120 s时,累计通量计算次数为7.1×107。综上,融合策略能有效结合动态网格控制策略和局部时间步长技术的优势,更大程度上减小累计通量计算次数。由于计算网格分布均匀,时间步长差异不大,与全局最小时间步长相比,使用融合策略能最大减少累计通量计算次数约20%。
图 6展示了沿坝址局部加密条件下,使用动态网格和局部时间步长融合算法在第20 s时局部时间步长层级(图 6a)和水深(图 6b)有效网格分布,其中有颜色部分为有效网格,空白区域为无效网格,不参与计算。当沿坝址局部加密时,加密区网格单元时间步长显著减小,与非加密区网格时间步长差异加大,使用局部时间步长技术成功地将网格分为3级进行计算与更新,可提升局部时间步长技术应用效果,同时动态网格控制策略排除了右侧大部分无效网格,进一步减少了模型计算量。

|
| 图 6 沿坝址局部加密第20 s时融合方法的局部时间步长级数和水深有效网格分布 |
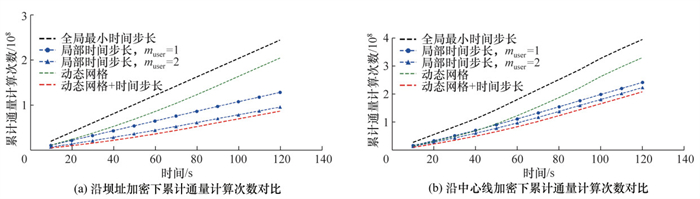
图 7为沿坝址、沿中心线两种局部加密方式下不同算法的模型累计通量计算次数对比。可以看出,当局部网格加密时,局部时间步长技术的使用效果显著优于动态网格控制策略。可见,两种方法融合后,动态网格控制策略能在局部时间步长技术的基础上进一步减少模型累计通量计算次数。不同局部加密方式的对比结果显示,当沿水槽中心线加密时细小网格更多,为保证模型计算的稳定性,导致有更多网格必须采用全局最小时间步长进行更新,细小网格数量的增多逐渐削弱了局部时间步长的应用效果。第120 s时,沿坝址加密条件下全局最小时间步长更新策略下累计通量计算次数为2.4×108,动态网格和局部时间步长融合策略下累计通量计算次数为8.6×107,融合算法节省通量计算次数约64%。沿中线加密条件下,全局最小时间步长更新策略下累计通量计算次数为3.9×108,动态网格和局部时间步长融合策略下累计通量计算次数为2.0×108,融合算法节省通量计算次数约48%。
|
| 图 7 非均匀三角形网格在不同算法条件下累计通量计算次数对比 |
表 1总结了理想溃坝算例在不同网格、不同加速策略下模型累计通量计算次数、模拟计算耗时。结果显示,模型模拟计算耗时与累计通量计算次数呈正比关系。沿中心线加密下网格数量最多,所需累计通量计算次数也最多,模拟计算耗时最高;各加速策略中,动态网格和局部时间步长(muser=2)融合策略的加速效果最好,表明融合策略能有效减少模型计算量,提高模型计算效率;表 1最后1行为与基准工况(全局最小时间步长)的计算次数/耗时相比,动态网格+局部时间步长(muser=2)策略的计算次数/计算耗时的节省量占比。由于各算法本身也会增加一部分模型计算量,故对应工况条件下实际模拟计算耗时结果略低于累计通量计算次数降低幅度,但加速效果仍很明显。
| 加速策略 | 累计通量计算次数/107 | 模拟耗时/s | |||||
| 均匀网格2 m | 沿坝址加密网格 | 沿中心线加密网格 | 均匀网格2 m | 沿坝址加密网格 | 沿中心线加密网格 | ||
| 全局最小时间步长 | 8.9 | 24.5 | 39.5 | 9.3 | 33.2 | 42.7 | |
| 局部时间步长(级数muser=1) | 7.8 | 12.8 | 24.2 | 9.1 | 16.5 | 33.5 | |
| 局部时间步长(级数muser=2) | 7.4 | 9.6 | 22.3 | 8.3 | 13.1 | 29.2 | |
| 动态网格 | 7.3 | 20.5 | 33.1 | 8.1 | 24.7 | 40.6 | |
| 动态网格+局部时间步长(级数muser=2) | 7.1 | 8.6 | 20.8 | 8.1 | 12.8 | 28.4 | |
| 融合策略相对于全局最小时间步长策略节省/% | 20.2 | 64.9 | 47.3 | 12.9 | 61.4 | 33.5 | |
2.2 南岗河流域洪涝模拟
南岗河流域位于广东省广州市黄埔区中部,是黄埔区内最大的流域,集雨面积115.99 km2。流域地势整体呈北高南低,地形高程范围为5~365 m。南岗河流域内除北部主要为山区外,大部分地区在规划的城市开发边界内,流域中城市开发边界内总面积为66.61 km2,占流域面积约60%。该流域由于硬化地面占比大,产汇流速度快,在遭遇暴雨过程时易形成局部内涝。
南岗河流域洪涝模拟模型由一维和二维水动力模型耦合组成。一维水动力模型为一维河网水动力模型和一维管网水动力模型。其中:一维河网水动力模型概化河段23段,总长度约72 km,设置汊点21个、河道断面731个,平均断面间距100 m,如图 8a所示;一维管网模型共概化雨水管道5 077段,检查井4 903个,见图 8b。河网和管网模型通过对应位置的河道断面进行耦合。一维模型的边界条件为流域降雨过程和河口水位过程,降雨由SWMM模型中的水文模块计算并转化为径流,通过检查井、雨水箅子进入洪涝模型体系;河口水位过程为南岗河口实测潮位过程,用于给定一维河网水动力模型的水位边界条件。

|
| 图 8 南岗河流域一维水动力模型设置 |
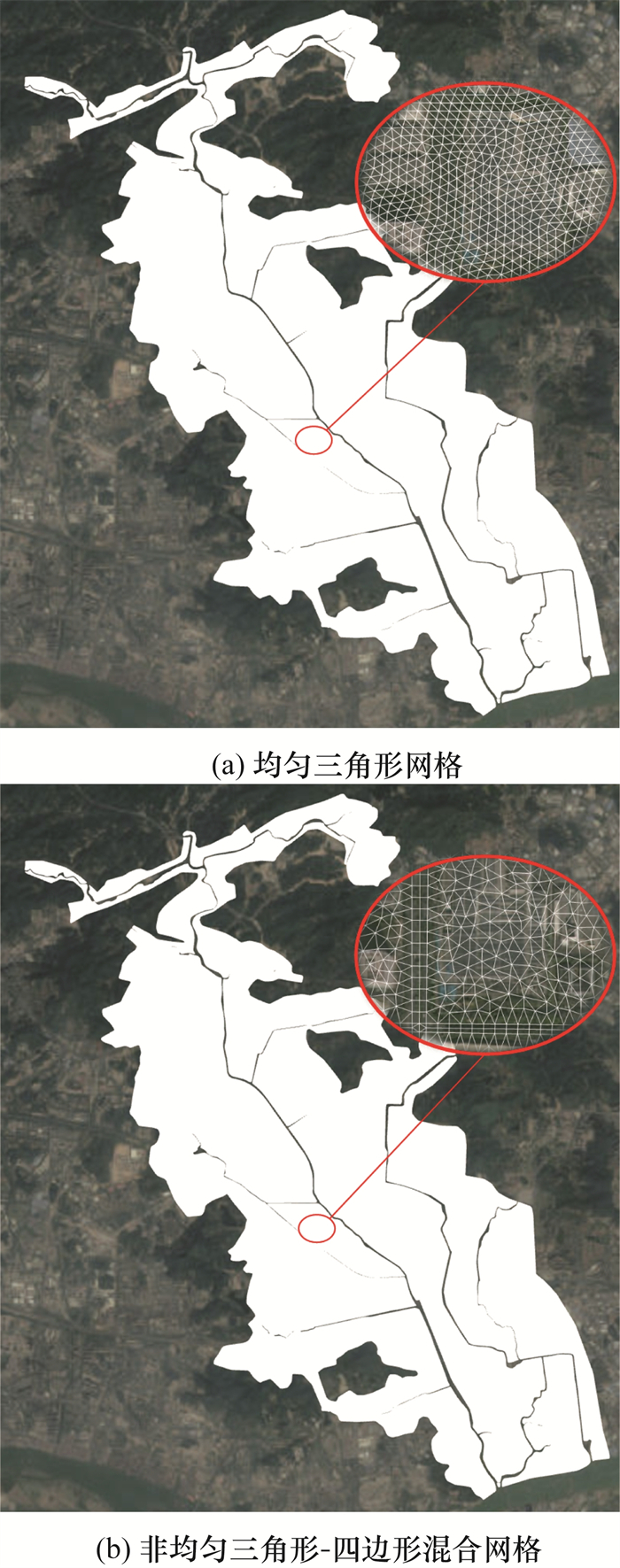
二维水动力模型为地表淹没模型,建模面积78.71 km2,采用非结构网格划分计算域。为充分探究实际应用时不同加速策略对网格的适应性,算例设置了2套不同的计算网格:1) 均匀三角形网格(图 9a),网格边长为20 m,网格总数434 931,节点总数223 412;2) 非均匀三角形-四边形混合网格(图 9b),最小边长5 m,最大35 m,网格总数291 950,节点总数159 157。二维水动力模型侧向上通过河道堤防与一维河网水动力模型耦合,垂向上通过检查井与一维管网模型耦合。
|
| 图 9 南岗河流域二维水动力模型网格设置 |
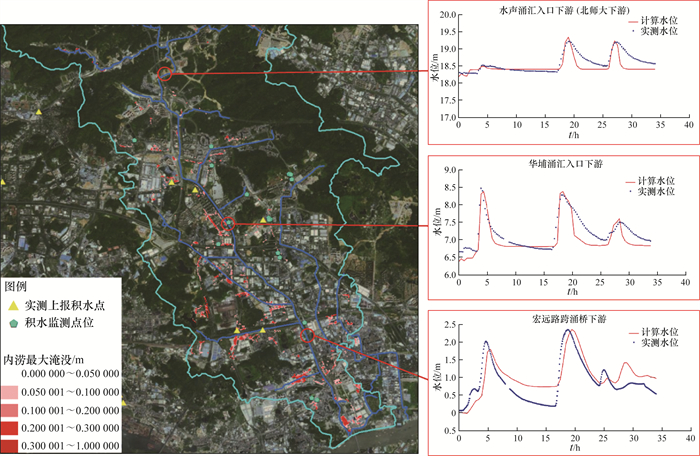
模型使用2023年6月14日场次暴雨进行率定。暴雨自6月13日14时始,至6月15日0时止,累计降雨量超200 mm,流域内局部地区内涝严重。洪涝模型模拟结果见图 10。洪涝模拟模型成功重演出南岗河干流上游(水声涌汇入口下游)、中游(华埔涌汇入口下游)、下游(宏远路跨涌桥下游)3个典型断面的暴雨洪水过程,最高水位误差均小于0.2 m,且模型计算结果体现出高密度城市小流域产汇流速度快、陡涨陡落的特征。由于短时强降雨引起河道水位陡涨,导致管网排水受河道顶托,地表内涝模拟的淹没范围主要集中在河涌水系沿岸。同时,两套网格下模型计算得到的内涝淹没范围差异不大,表明此算例条件下,模型的网格适应性较好,且非均匀网格能够对重点区域进行局部加密,在减少网格总数的同时,保证了模拟效果。
|
| 图 10 南岗河流域洪涝模拟结果与实测结果对比 |
表 2统计了南岗河流域洪涝模拟时使用不同网格在不同加速策略下模型计算耗时。相较于全局最小时间步长更新策略,在均匀三角形网格条件下局部时间步长技术(muser=2)能提升模型计算效率约26.5%,动态网格控制策略能提升计算效率约61.1%,局部时间步长与动态网格融合使用时,模型计算效率提升更加明显,节省计算耗时约64.5%;非均匀三角形-四边形混合网格条件下,局部时间步长技术(muser=2)能节省计算耗时约30.5%,动态网格控制策略能节省计算耗时约46.2%,局部时间步长与动态网格融合使用时,模型计算效率提升更加明显,节省计算耗时约59.1%。表 2结果表明,局部时间步长与动态网格融合算法能够发挥算法优势,当淹没面积少时,动态网格的作用效果更好,当计算网格数量多时,局部时间步长技术效果明显。可见,融合算法在城市区域内涝模拟中性能良好。
| 网格设置 | 计算耗时/min | |||
| 全局最小时间步长 | 局部时间步长(muser=2) | 动态网格 | 动态网格+ 局部时间步长(muser=2) | |
| 均匀三角形网格 | 532 | 391 | 207 | 189 |
| 非均匀三角形-四边形混合网格 | 210 | 146 | 113 | 86 |
3 结论
二维水动力模型是城市洪涝模拟模型的关键组成部分,但是精细化城市洪涝模拟过程中,由于需要精细刻画局部地形变化,计算网格尺度较小,网格数量多,并且计算时间步长小,导致洪涝模拟模型计算耗时偏高,制约了洪涝模拟模型的进一步应用。
城市洪涝过程往往出现散状分布的局部淹没区,适合动态网格控制策略的应用;同时,洪涝模拟时还需要局部网格细化,使模型能更好地反映局部易涝区的地形差异变化,但也会导致不同网格允许的最大时间步长差异较大,适合局部时间步长技术的应用。本文以自主开发的洪涝模拟模型为基础,提出了动态网格控制策略和局部时间步长技术融合算法,使模型能够自动调整有效单元组并对有效单元使用组局部时间步长技术。本文算法融合两种算法优势,进一步减少模型计算量,提高计算效率。采用理想溃坝算例和南岗河流域洪涝模拟典型场景,对多种加速策略从计算精度、计算效率等方面进行了对比分析。计算结果表明,动态网格控制策略、局部时间步长均能有效提高模型计算效率。有效单元组数量少时,动态网格控制策略效果明显;时间步长差异较大时,局部时间步长技术效果更优;动态网格控制策略与局部时间步长算法融合后,能进一步减少模型计算量,相对于单一动态网格策略或局部时间步长技术优势明显,在南岗河流域的实际应用案例中能够节省计算耗时约60%。
但是,由于不同算法的适用场景有所不同,受计算区域、网格条件等影响,动态网格控制策略、局部时间步长技术、融合算法的适用效果均会变化。例如,使用二维水动力模型仅模拟河道洪水、河口等区域时,动态网格控制策略的效果可能不明显;当计算区域网格分布均匀、水流流态稳定时,局部时间步长技术可能效果一般。融合算法能够结合上述两种算法优势,但是同时拥有上述算法的固有缺点,因此实际应用时应根据具体场景选择合适的算法,以达到更高的模拟效果和计算效率。当动态网格控制策略和局部时间步长技术均无明显效果时,可考虑使用并行计算技术,充分利用计算机硬件性能来提高模型的计算效率。例如,可使用OpenMP多核CPU并行、CUDA GPU并行技术,将大量计算分配至不同的线程中并行计算,从而节省计算时间。
| [1] |
张建云, 王银堂, 贺瑞敏, 等. 中国城市洪涝问题及成因分析[J]. 水科学进展, 2016, 27(4): 485-491. ZHANG J Y, WANG Y T, HE R M, et al. Discussion on the urban flood and waterlogging and causes analysis in China[J]. Advances in Water Science, 2016, 27(4): 485-491. (in Chinese) |
| [2] |
徐宗学, 叶陈雷. 城市暴雨洪涝模拟: 原理、模型与展望[J]. 水利学报, 2021, 52(4): 381-392. XU Z X, YE C L. Simulation of urban flooding/waterlogging processes: Principle, models and prospects[J]. Journal of Hydraulic Engineering, 2021, 52(4): 381-392. (in Chinese) |
| [3] |
宋利祥, 徐宗学. 城市暴雨内涝水文水动力耦合模型研究进展[J]. 北京师范大学学报(自然科学版), 2019, 55(5): 581-587. SONG L X, XU Z X. Coupled hydrologic-hydrodynamic model for urban rainstorm water logging simulation: Recent advances[J]. Journal of Beijing Normal University (Natural Science), 2019, 55(5): 581-587. (in Chinese) |
| [4] |
吴珊, 赵玉杰, 王昊, 等. 基于运动波模拟的雨水管网设计流量计算方法[J]. 清华大学学报(自然科学版), 2023, 63(11): 1887-1896. WU S, ZHAO Y J, WANG H, et al. Calculation method for stormwater network design flow based on kinematic wave simulation[J]. Journal of Tsinghua University (Science and Technology), 2023, 63(11): 1887-1896. (in Chinese) |
| [5] |
印定坤, 陈正侠, 李骐安, 等. 降雨特征对多雨城市海绵改造小区径流控制效果的影响[J]. 清华大学学报(自然科学版), 2021, 61(1): 50-56. YIN D K, CHEN Z X, LI Q A, et al. Influence of rainfall characteristics on runoff control of a sponge reconstructed community in a rainy city[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(1): 50-56. (in Chinese) |
| [6] |
邵蕊, 邵薇薇, 苏鑫, 等. 基于TELEMAC-2D模型分析不同洪涝情景对城市应急响应时间的影响[J]. 清华大学学报(自然科学版), 2022, 62(1): 60-69. SHAO R, SHAO W W, SU X, et al. Impact of various flood scenarios on urban emergency responses times based on the TELEMAC-2D model[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(1): 60-69. (in Chinese) |
| [7] |
邵薇薇, 刘家宏, 王开博, 等. 基于情景模拟的城市洪涝交通影响评估[J]. 清华大学学报(自然科学版), 2022, 62(10): 1591-1605. SHAO W W, LIU J H, WANG K B, et al. Assessment of urban flood impact on traffic flow based on scenario simulations[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(10): 1591-1605. (in Chinese) |
| [8] |
KIM B, SANDERS B F, FAMIGLIETTI J S, et al. Urban flood modeling with porous shallow-water equations: A case study of model errors in the presence of anisotropic porosity[J]. Journal of Hydrology, 2015, 523: 680-692. DOI:10.1016/j.jhydrol.2015.01.059 |
| [9] |
王俊珲, 侯精明, 同玉, 等. 局部时间步长与GPU加速的非均匀网格模型在内涝模拟中的应用[J]. 水动力学研究与进展, 2023, 38(5): 718-728. WANG J H, HOU J M, TONG Y, et al. Application of local time step and GPU-accelerated non-uniform grid model in waterlogging simulation[J]. Chinese Journal of Hydrodynamics, 2023, 38(5): 718-728. (in Chinese) |
| [10] |
许栋, 徐彬, PAYET D, 等. 基于GPU并行计算的浅水波运动数值模拟[J]. 计算力学学报, 2016, 33(1): 114-121. XU D, XU B, PAYNET D, et al. Numerical simulation of shallow water motion based on parallel computation using GPU[J]. Chinese Journal of Computational Mechanics, 2016, 33(1): 114-121. (in Chinese) |
| [11] |
赵自雄, 胡鹏. 基于并行算法和局部时间步长技术的二维浅水模拟[C]//第19届中国海洋(岸)工程学术讨论会论文集(下). 重庆: 海洋出版社, 2019: 4. ZHAO Z X, HU P. Two-dimensional shallow water simulation based on parallel algorithms and local time step technology[C]//Proceedings of the 19th China Ocean (Shore) Engineering Academic Symposium (Part 2). Chongqing: Ocean Press, 2019: 4. (in Chinese) |
| [12] |
WU J X, HU P, ZHAO Z X, et al. A GPU-accelerated and LTS-based 2D hydrodynamic model for the simulation of rainfall-runoff processes[J]. Journal of Hydrology, 2023, 623: 129735. DOI:10.1016/j.jhydrol.2023.129735 |
| [13] |
JUDI D R, BURIAN S J, MCPHERSON T N. Two-dimensional fast-response flood modeling: Desktop parallel computing and domain tracking[J]. Journal of Computing in Civil Engineering, 2011, 25(3): 184-191. DOI:10.1061/(ASCE)CP.1943-5487.0000064 |
| [14] |
HOU J M, WANG R, JING H X, et al. An efficient dynamic uniform Cartesian grid system for inundation modeling[J]. Water Science and Engineering, 2017, 10(4): 267-274. DOI:10.1016/j.wse.2017.12.004 |
| [15] |
SANDERS B F. Integration of a shallow water model with a local time step[J]. Journal of Hydraulic Research, 2008, 46(4): 466-475. DOI:10.3826/jhr.2008.3243 |
| [16] |
HU P, LEI Y L, HAN J J, et al. Improved local time step for 2D shallow-water modeling based on unstructured grids[J]. Journal of Hydraulic Engineering, 2019, 145(12): 6019017. DOI:10.1061/(ASCE)HY.1943-7900.0001642 |
| [17] |
胡鹏, 韩健健, 雷云龙. 基于局部分级时间步长方法的水沙耦合数学模拟[J]. 浙江大学学报(工学版), 2019, 53(4): 743-752. HU P, HAN J J, LEI Y L. Coupled modeling of sediment-laden flows based on local-time-step approach[J]. Journal of Zhejiang University (Engineering Science), 2019, 53(4): 743-752. (in Chinese) |
| [18] |
胡鹏, 姬奥飞, 陶俊余. 基于局部时间步长方法的潮流数值模型研究及应用[J]. 海洋工程, 2020, 38(1): 111-119. HU P, JI A F, TAO J Y. Numerical simulation of tidal flows based on the local-time step approach[J]. The Ocean Engineering, 2020, 38(1): 111-119. (in Chinese) |
| [19] |
TINH N X, TANAKA H, YU X P, et al. Numerical implementation of wave friction factor into the 1D tsunami shallow water equation model[J]. Coastal Engineering Journal, 2021, 63(2): 174-186. DOI:10.1080/21664250.2021.1919391 |
| [20] |
黄国如, 陈文杰, 喻海军. 城市洪涝水文水动力耦合模型构建与评估[J]. 水科学进展, 2021, 32(3): 334-344. HUANG G R, CHEN W J, YU H J. Construction and evaluation of an integrated hydrological and hydrodynamics urban flood model[J]. Advances in Water Science, 2021, 32(3): 334-344. (in Chinese) |
| [21] |
GUO K H, GUAN M F, YU D P. Urban surface water flood modelling: A comprehensive review of current models and future challenges[J]. Hydrology and Earth System Sciences, 2021, 25(5): 2843-2860. DOI:10.5194/hess-25-2843-2021 |
| [22] |
陈文龙, 宋利祥, 邢领航, 等. 一维-二维耦合的防洪保护区洪水演进数学模型[J]. 水科学进展, 2014, 25(6): 848-855. CHEN W L, SONG L X, XING L H, et al. A 1D-2D coupled mathematical model for numerical simulating of flood routine in flood protected zone[J]. Advances in Water Science, 2014, 25(6): 848-855. (in Chinese) |
| [23] |
金溪, 周鹏飞, 张翔凌, 等. 基于改进垂向流量交换的城市内涝模拟方法[J]. 水科学进展, 2023, 34(2): 218-226. JIN X, ZHOU P F, ZHANG X L, et al. A coupling 1D-2D model of urban flooding simulation based on improved vertical flow exchange method[J]. Advances in Water Science, 2023, 34(2): 218-226. (in Chinese) |



