2. 北京控制与电子技术研究所, 北京 100038
2. Beijing Institute of Control & Electronic Technology, Beijing 100038, China
随着人类对太空探索的逐步深入,小行星已成为科研学者们关注的焦点[1-2]。作为太阳系形成初期形成的小天体,小行星有助于人类理解太阳系的形成与演化,同时也是揭示地球生命起源问题的关键[3-4]。小行星不仅具有重要的科学研究价值,其包含的稀有金属等物质也具有极高的经济价值[5]。此外,小行星也是威胁地球安全的因素之一。同时,近地小行星被认为是毁灭人类文明的七大威胁之一[6]。2013年,一颗直径仅为17~20 m的近地小行星撞击俄罗斯车里雅宾斯克地区,致使约1 500人受伤,3 000多栋房屋受损[7-8]。因此,小行星防御是目前航天领域的热门研究方向[9]。
Bus等[10]利用远程方法研究了一些直径较大的近地小行星的物理特性,但研究范围十分有限;同时发现,监测直径较小、距离较远或观测条件较差的小行星难度大,此类远程方法难以获得足够数据开展进一步研究,目前直径20 m级的近地小行星编目率不足1%[6]。为获取更多详细可靠的小行星数据,需派遣探测器近距离观测小行星。同时,对于小行星防御、小行星采矿等研究领域,也需派遣航天器执行小行星撞击、着陆、采样等任务。目前,各国均在积极开展小行星探测、撞击等航天任务。如日本的隼鸟2号小行星探测器成功登陆了小行星162173,并进行采样将样本带回地球[11]。美国也开展了针对双星系统的小行星撞击任务DART(the double asteroid redirection test)[12]。
本文以中国首个小行星撞击任务为背景[13],针对直径约30 m的小直径目标小行星开展撞击前的目标搜索方案研究。小行星撞击任务可大致分为巡航阶段和接近阶段。在巡航阶段,撞击器按照既定转移轨道由地球转移至目标小行星附近。在接近阶段,撞击器需利用自身观测设备,如光学相机,捕获目标小行星。对于直径较大的目标小行星,如DART任务的目标为双星系统,主星直径约为780 m,直径较大,因此易于获得充足的前期观测数据,可准确确定其轨道信息。在接近阶段的初始阶段,撞击器只需将相机指向目标小行星的星历位置,便可保证目标小行星出现在视野范围内。因此,对于大直径目标,目前研究更关注制导控制律的设计[14-15]。而对于直径较小或观测数据较少的目标小行星,其星历信息误差较大,撞击器仅利用星历信息无法准确捕获目标小行星,即当撞击器按照星历位置调整相机指向后,目标小行星仍位于相机视野范围之外,此时需采用快速有效的搜索策略,调整相机指向,使目标小行星出现在相机视野内。
由于撞击器与目标小行星的相对速度较大,整个接近阶段以及最终的撞击需在约4 000.0 s内完成,因此搜索方案需满足一定的时间限制。同时,由于参数限制,相机在撞击器姿态机动过程中无法成像;且拍摄的图像信息需由撞击器星载计算机自主处理,以便进行自主导航,故相机需在满足区域覆盖限制的前提下使成像次数最小化,以降低星载计算机的运算需求,同时减少搜索耗时。
对于目标搜索问题,一些学者进行了相关研究。Cano等[16]考虑了搜索时间与燃料消耗等限制,设计了利用光学相机在大范围区域内搜索目标小行星的扫描搜索策略。但该方案搜索时间过长,无法满足本次撞击任务的时间限制。一些地球轨道目标的搜索策略也可应用于小行星搜索,其中螺旋扫描是常用的搜索策略[17-18]。通过绕指定方向旋转检测仪器的光轴进行螺旋扫描可实现快速高效地覆盖区域,该搜索策略在雷达搜索等领域应用广泛。此外,You等[19]设计了7种太空碎片搜索策略,并利用Monte Carlo仿真实验,验证了这些策略可在几分钟内捕获目标,且成功率高达99.9%。Hu等[20]利用遗传算法,设计了可在地球同步轨道观测大气变化的扫描搜索方案。一些人造地球观测卫星的扫描搜索策略也可提供参考[21-22]。甘岚等[23]利用遗传算法为人造太阳同步轨道卫星设计了目标区域成像策略,提高了计算效率。Zhi等[24]设计了可用于人造小卫星的对地观测扫描方案,该方案利用卫星自旋、轨道运动及相机的摇摆可有效拓宽对地观测卫星的覆盖区域。同时,也可利用人造敏捷卫星的快速机动能力,通过优化其机动路径,实现大范围搜索目标的目的[25-29]。但上述地球轨道目标搜索方案要求相机可在机动过程中成像,超出了本次任务中相机的性能极限,即在成像时撞击器角速度小于0.01(°)/s,近似为零。并且其星载计算机通常无须处理图像数据,因此其成像数量较多,而本次任务的星载计算机需自主处理成像图片,且单张图像最长处理耗时为0.5 s,若成像数量较多,则星载计算机无法及时处理图像,故上述方案也超出了本次任务计算机性能的极限。
针对上述问题,本文在考虑搜索耗时与成像间隔等限制的前提下,即总搜索耗时须小于整个接近段的1/10,即400.0 s,相机成像时间间隔须大于0.5 s,设计了一种可最大化单次成像面积的扫描搜索方案。通过调整搜索次数,该方案可覆盖不同面积的目标区域,并给出了不同搜索次数下可覆盖区域面积的解析表达式。同时,本文给出了不同视野位置的递推计算方法;利用数值仿真,验证了所提搜索方案的有效性。
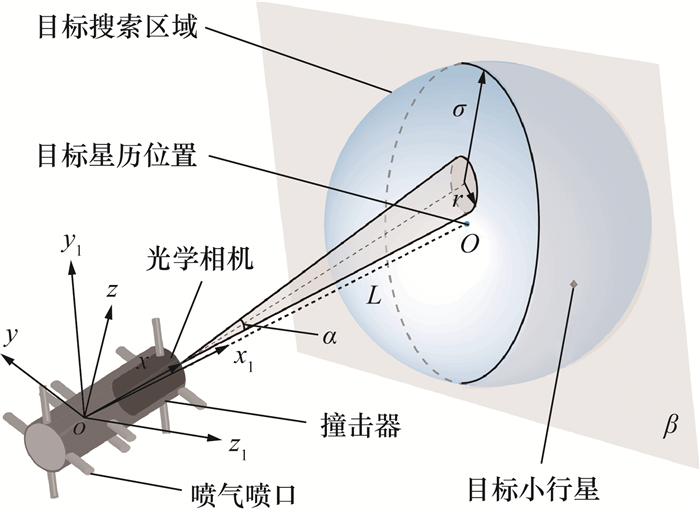
1 简化搜索模型 1.1 撞击器模型如图 1所示,撞击器本体系原点位于其质心,x、y、z轴分别平行于其惯量主轴方向。根据前期观测数据, 可确定目标小行星的定轨误差小于确定常数σ, 即目标区域为以当前时刻小行星的星历位置O为球心, 半径为σ的球形区域。o-x1y1z1为固连系, 其原点位于撞击器质心, x1、y1、z1轴与初始时刻本体系x、y、z轴重合。过O点垂直于x1轴作平面β, 相机视场在β上投影半径为r。α为光学相机视场角, L为撞击器质心与O点的相对距离。
|
| 图 1 目标搜索示意图 |
撞击器惯量矩阵J在本体系下可表示为
| $ \boldsymbol{J}=\left[\begin{array}{ccc} A_{0} & 0 & 0 \\ 0 & B_{0} & 0 \\ 0 & 0 & C_{0} \end{array}\right]. $ | (1) |
其中A0、B0、C0分别为撞击器相对于x、y、z轴的转动惯量。
光学相机光轴沿本体系x轴方向延伸。同时,撞击器采用喷气方式控制姿态,其可沿本体系x、y、z轴施加正反方向的控制力矩,且每个坐标轴的力矩分为2个分力矩,分别为Mx1,My1,Mz1,Mx2,My2,Mz2。
1.2 搜索模型如图 1所示,由于目标小行星定轨误差较大,相机视场无法完全覆盖目标可能出现的区域,需调整相机指向搜索整个目标区域。
假设搜索开始时刻,光学相机光轴指向O,此时x1轴指向O。固连系在搜索过程中不发生旋转,只跟随质心进行平动。由于在接近阶段,撞击器与目标小行星的相对距离远小于二者的轨道半径。此时,撞击器相对于目标星历位置的运动可简化为沿本体系x1轴方向的直线运动。同时,在搜索过程中,撞击器不进行轨道机动。因此目标区域在oy1z1平面无相对运动,O点时刻位于x1轴上。初始时刻r表示如下:
| $ r=L \cdot \tan \frac{\alpha}{2} . $ | (2) |
由于σ≪L,可忽略x1轴方向的定轨误差,此时搜索区域可简化为平面β上一个半径为σ的二维圆形区域γ。为简化计算,假设r在搜索过程中保持不变,此时,扫描搜索方案可表述为利用尽量少的半径为r的圆覆盖半径为σ的圆形目标区域γ。
2 搜索方案设计本章根据上述简化搜索模型,为不同面积的目标区域设计搜索覆盖方案,并给出不同搜索次数可覆盖区域面积的解析表达式。同时,根据不同搜索次数,本章将给出相机视野在平面β上圆心位置的计算方法。
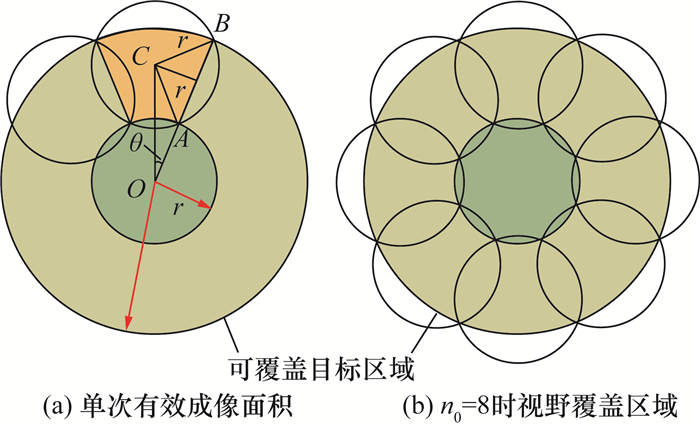
2.1 单层搜索方案 2.1.1 单层搜索方案可覆盖面积计算初始时刻,相机视场圆心位于O处。为增大覆盖面积,减少机动时间,可在初始视野外围依次成像。为简化计算,假设初始视野外圈均匀分布n0个新视野。通常情况下,目标定轨误差远大于相机视野半径,因此,单层搜索方案需尽量扩大可覆盖区域。如图 2所示,为防止出现遗漏区域并尽量扩大成像范围,外围各视野的内层交点A需恰好落在初始视野边缘。此时,外层交点B所处位置即为可覆盖区域边界。
|
| 注:图中橙色部分为单次有效成像面积。 图 2 单层搜索方案 |
为计算图 2a中n0的最佳取值,定义单次有效成像面积S0在初始视野范围外,每个新视野可覆盖的目标区域面积表示如下:
| $ \left\{\begin{array}{l} O B=O A+A B=r+2 r \cos \angle C A B, \\ \angle C A B=\angle A O C+\angle O C A, \\ S_{0}=\frac{\pi\left(O B^{2}-r^{2}\right)}{n_{0}}. \end{array}\right. $ | (3) |
最终可推导出S0的计算公式为
| $ \begin{gather*} S_{0}=\frac{\pi r^{2}\left((2 \cos 2 \theta+1)^{2}-1\right)}{n_{0}}, \\ \theta=\pi / n_{0} . \end{gather*} $ | (4) |
其中θ为初始视野与外围视野交点圆心角的一半。
通过最大化S0,可计算得到n0的最佳取值为8。图 2b展示了n0=8时相机视野可覆盖的最大区域,其面积S1为
| $ S_{1}=(2 \cos 2 \theta+1)^{2} \pi r^{2} . $ | (5) |
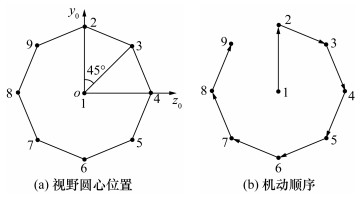
如图 3a所示,初始视野圆心编号为1,外围8个新视野圆心编号分别为2~9。外围视野圆心与初始视野圆心的直线距离L0均为2rcosπ/8。以初始圆心位置为原点,建立平面坐标系oy0z0,其中y0、z0轴分别平行于y1、z1轴。
|
| 图 3 单层搜索方案视野圆心位置与机动顺序示意图 |
首先计算2号圆的圆心位置。设2号圆心位于y0轴上,根据1号与2号圆心间的距离,可得到2号圆心在oy0z0平面的坐标为
| $ \left(y_{2}, z_{2}\right)=\left(0, 2 r \cos \frac{\pi}{8}\right) . $ | (6) |
同时,由于外围8个视野均匀分布,因此,相邻2个外围圆心与初始圆心连线的夹角均为45°。根据上述关系,利用递推方法,可依次计算剩余圆心位置,其计算过程如下:
1) 对于i (i=3, 4, 5, …, 9) 号圆心位置(yi, zi),首先确定1号及i-1号圆心位置(y1, z1)、(yi-1, zi-1)。
2) 计算(y1, z1)、(yi-1, zi-1)两点连线与z0轴正方向的夹角φ0为:
| $ {\varphi _0} = \left\{ \begin{array}{l} \arctan \left( {\frac{{{y_{i - 1}} - {y_1}}}{{{z_{i - 1}} - {z_1}}}} \right), {z_{i - 1}} - {z_1} > 0;\\ \arctan \left( {\frac{{{y_{i - 1}} - {y_1}}}{{{z_{i - 1}} - {z_1}}}} \right) + \pi , \\ \;\;\;\;\;\;\;\;\;\;{y_{i - 1}} - {y_1} \ge 0, {z_{i - 1}} - {z_1} < 0;\\ \arctan \left( {\frac{{{y_{i - 1}} - {y_1}}}{{{z_{i - 1}} - {z_1}}}} \right) - \pi , \\ \;\;\;\;\;\;\;\;\;\;{y_{i - 1}} - {y_1} < 0, {z_{i - 1}} - {z_1} < 0;\\ \frac{\pi }{2}, \;\;\;\;\;\;\;\;{y_{i - 1}} - {y_1} > 0, {z_{i - 1}} - {z_1} = 0;\\ - \frac{\pi }{2}, \;\;\;\;\;\;{y_{i - 1}} - {y_1} < 0, {z_{i - 1}} - {z_1} = 0. \end{array} \right. $ | (7) |
3) 计算(y1, z1)、(yi, zi)两点连线与z0轴正方向夹角φ为
| $ \begin{gather*} \varphi=\varphi_{0}-\frac{\pi}{4}, \quad \varphi \in(-\pi, \pi] ; \\ \varphi=\varphi+2 \pi, \quad \varphi \leqslant-\pi . \end{gather*} $ | (8) |
4) 计算(yi, zi)点坐标为
| $ \begin{align*} & y_{i}=y_{1}+L_{0} \cos \varphi , \\ & z_{i}=z_{1}+L_{0} \sin \varphi . \end{align*} $ | (9) |
重复上述过程,即可计算出剩余圆心位置。在搜索过程中,需调整相机光轴指向,使其恰好通过平面β上相应的圆心位置。图 3b展示了相机光轴的机动顺序,即光轴依次经过1—9号位置,即可完成目标区域搜索。
2.2 双层搜索方案 2.2.1 双层搜索方案可覆盖面积计算为进一步扩大视野覆盖区域,需在单层搜索方案的基础上,继续在外围增加新视野。
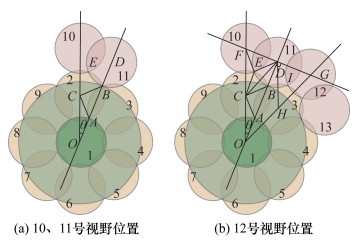
如图 4所示,为尽量增大可覆盖面积,11号视野边缘应落在单层搜索方案外围交点B处。为简化后续圆心位置的计算过程,假设11号视野圆心位于直线OA上,此时便可确定11号圆心的位置D。同时,11号视野与2号视野相交于E点。设10号视野圆心F位于直线OC上,且与2号、11号视野相交于E点。为计算新视野圆心坐标,需计算∠DCF。
|
| 图 4 双层搜索方案视野位置计算示意图 |
由图 4可知,线段OA=AC=CB=BD=CE= DE=EF=r。因此,△OAC、△ABC均为等腰三角形,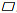
| $ \left\{\begin{array}{l} \angle A O C=\angle O C A=\angle F C E=\frac{\pi}{8}, \\ \angle C A B=\angle C B A=\angle B C E=\frac{\pi}{4}. \end{array}\right. $ | (10) |
根据菱形性质,其对角线平分对角,因此最终可计算得到
| $ \angle D C F=\angle F C E+\frac{1}{2} \angle B C E=\frac{\pi}{4} . $ | (11) |
同时,可计算出线段CF与CD的长度为
| $ C F=C D=2 r \cos \frac{\pi}{8} . $ | (12) |
即10号、11号视野与2号视野的圆心距离均为L0。
同理,在11号视野右侧增加12号视野,其圆心位于直线OH上(H为3号视野圆心),且与3号、11号视野相交于I点。12号圆心位置为G。同理可证明∠DHG=π/4,且12号视野与3号视野的圆心距为L0。
如图 5a所示,继续顺时针增加新视野,13号视野与11号相似,其圆心M位于直线ON上,边缘位置落在3、4号视野外围交点P处。3号与12号视野交点为J,为防止出现遗漏区域,应使J点位于13号视野内。
|
| 图 5 双层搜索方案视野位置计算与覆盖面积示意图 |
设直线MJ与13号视野边缘交点为K,则需MK≥MJ。其证明过程如下。
根据前文∠DCF计算方法,可计算得到:
| $ \left\{\begin{array}{l} \angle H G J=\angle G O M=\frac{\pi}{8}, \\ O G=O H+H G=4 r \cos \frac{\pi}{8}, \\ O M=O P+P M=2 r \cos \frac{\pi}{4}+2 r. \end{array}\right. $ | (13) |
在三角形OMG中,依据余弦定理,可计算线段MG的长度为
| $ \begin{gather*} M G=\sqrt{O G^{2}+O M^{2}-2 O G \cdot O M \cdot \cos \frac{\pi}{8}}= \\ 2 r \cos \frac{\pi}{4} . \end{gather*} $ | (14) |
同时,根据正弦定理可得
| $ \frac{M G}{\sin \angle M O G}=\frac{O M}{\sin \angle O G M} . $ | (15) |
因此,可算得∠OGM=3π/8。进而可得∠MGJ为
| $ \angle M G J=\angle O G M-\angle H G J=\frac{\pi}{4} . $ | (16) |
在△MGJ中,同样利用余弦定理,可计算出MJ的长度为r,即MK=MJ。因此,13号视野边缘恰好落在J处,满足覆盖要求。将上述视野覆盖方案围绕单层搜索方案一周,即可得到图 5b所示的双层搜索方案。其相关角度、圆心距等证明过程与本节证明流程一致,此处不再赘述。该方案可覆盖的最大面积S2为
| $ S_{2}=(8 \cos 2 \theta+4 \sin 2 \theta+9) \pi r^{2} . $ | (17) |
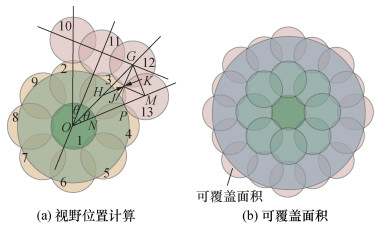
如图 6a所示,新增加的16个视野编号分别为10~25。首先计算10号圆心位置。由于其位于直线OC上,且与2号视野的圆心距为L0,因此,其在oy0z0平面的坐标为
| $ \left(y_{10}, z_{10}\right)=\left(0, 4 r \cos \frac{\pi}{8}\right) . $ | (18) |
|
| 图 6 双层搜索方案视野圆心位置与机动顺序示意图 |
通过式(10)和(11)证明可知,∠DCF为π/4,对应在图 6a中,即为10、11号圆心与2号圆心连线的夹角,为π/4。同时,由于11号与2号的圆心相距L0。因此,采用单层搜索方案圆心位置计算流程,利用10号和2号圆心位置,即可计算出11号圆心位置。同理,可利用3号和11号的圆心位置,计算出12号圆心位置。其证明过程同前文∠DCF证明,即式(10)和(11),此处不再赘述。最终可总结出双层搜索方案外围圆心位置计算流程如下:
1) 对于i (i=11, 12, 13, …, 25) 号圆心位置(yi, zi),首先确定j号及i-1号圆心位置(yj, zj)、(yi-1, zi-1)。其中编号j的计算公式为
| $ j=\operatorname{ceil}[(i-9) / 2]+1 . $ | (19) |
其中ceil为向上取整函数。
2) 利用式(7),计算(yj, zj)、(yi-1, zi-1)两点连线与z0轴正方向夹角φ0。
3) 利用式(8),计算(yj, zj)、(yi, zi)两点连线与z0正方向的夹角φ。
4) 利用式(9),计算(yi, zi)点坐标。
重复上述过程,即可计算出剩余圆心位置。图 6b展示了相机光轴的机动顺序,即光轴按箭头指示依次通过对应编号位置,即可完成目标区域搜索。
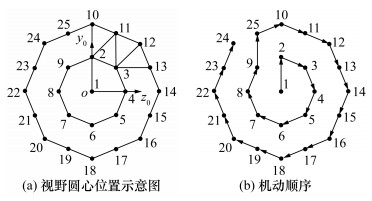
2.3 多层搜索方案在双层搜索方案外围继续增加新视野,可进一步增大搜索范围。本节结合4层搜索方案视野圆心位置示意图,介绍多层搜索方案视野位置确定原则。多层搜索方案圆心位置计算流程如下:
1) 对于第n层视野,首先确定该层起始视野圆心,其位于y0轴上,编号为(2n-1)2+1,且在oy0z0平面的坐标为
| $ \left(y_{(2 n-1)^{2}+1}, z_{(2 n-1)^{2}+1}\right)=\left(0, 2 n \cdot r \cos \frac{\pi}{8}\right) . $ | (20) |
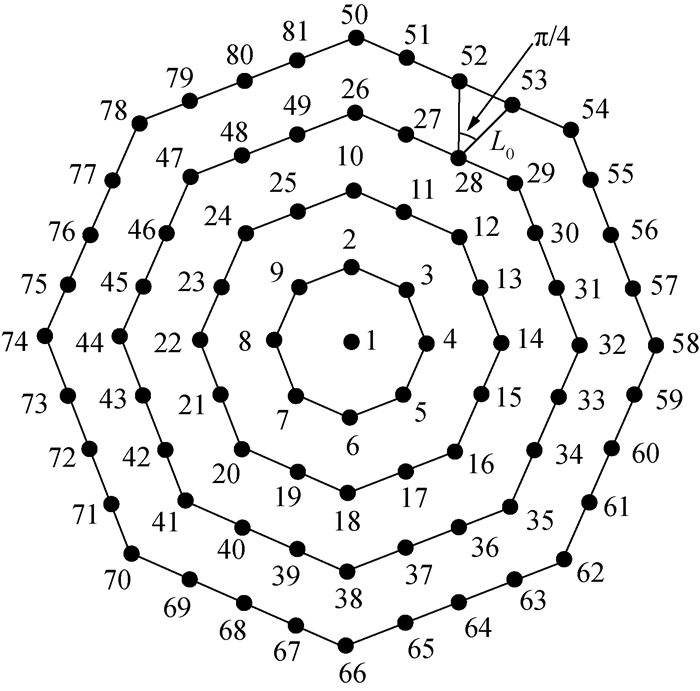
该层剩余圆心位置自起始位置顺时针依次递增编号,即(2n-1)2+2, (2n-1)2+3, …, (2n+1)2。以n=4为例,其起始位置编号为(2n-1)2+1=50,圆心坐标为(0, 8rcosπ/8)。其余位置编号依次为(2n-1)2+2=51,(2n-1)2+3=52,…,(2n+1)2=81。
2) 对于i (i=(2n-1)2+2, (2n-1)2+3,…,(2n+1)2) 号圆心位置(yi, zi),需确定j号及i-1号圆心位置(yj, zj)、(yi-1, zi-1)。其中编号j表示如下:
| $ \begin{gather*} q=\text{mod} \left[\left(i-(2 n-1)^{2}\right), n\right] ; \\ j=\left\{\begin{array}{l} (2 n-3)^{2}+\operatorname{ceil}\left[\left(i-(2 n-1)^{2}\right) / n\right] \cdot(n-1), q=0; \\ (2 n-3)^{2}+\left\{\operatorname{ceil}\left[\left(i-(2 n-1)^{2}\right) / n\right]-1\right\} \cdot \\ (n-1)+1, q=1, 2 ; \\ (2 n-3)^{2}+\left\{\operatorname{ceil}\left[\left(i-(2 n-1)^{2}\right) / n\right]-1\right\} \cdot \\ (n-1)+q-1, q \neq 0, 1, 2. \end{array}\right. \end{gather*} $ | (21) |
其中q为i-(2n-1)2整除n的余数。
式(21)中编号j的计算公式分为3种情况:第1种情况对应的是拐点前一个点位,即图 7中53、57、61、65、69、73、77、81号圆心位置。以53号圆心位置为例,其对应的j值为28。如图 7所示,52、53号圆心位置与28号圆心位置连线的夹角为π/4,53号与28号圆心距为L0(其证明过程同双层搜索方案,此处不再赘述),因此,可利用28与52号圆心位置计算53号圆心位置。第2种情况对应的是拐点及拐点后一个点位,即54、58、62、66、70、74、78及55、59、63、67、71、75、79号圆心位置。其余位置则为第3种情况。
|
| 图 7 4层搜索方案视野圆心位置示意图 |
2) 利用式(7),计算(yj, zj)、(yi-1, zi-1) 两点连线与z0轴正方向夹角φ0。
3) 利用式(8),计算(yj, zj)、(yi, zi)两点连线与z0正方向夹角φ。
4) 利用式(9),计算(yi, zi)点坐标。
重复上述过程,即可计算出剩余圆心位置。
对于n (n=1,2,…,N) 层搜索方案,其可覆盖的最大面积Sn为:
| $ S_{n}=\left\{\begin{array}{l} {\left[(n+1) \cos \frac{\pi}{4}+n\right]^{2} \pi r^{2}}, \\ n=2 k+1, k \in z ; \\ {\left[2 n^{2} \cos \frac{\pi}{4}+2 n \sin \frac{\pi}{4}+n+1\right] \pi r^{2}}, \\ n=2 k, k \in z, k>1. \end{array}\right. $ | (22) |
最终,根据目标搜索区域γ的面积大小关系,选择可完全覆盖目标区域的最小搜索层数n,便可实现目标区域覆盖搜索。目标搜索区域γ的面积大小关系为
| $ S_{n-1}<S_{\gamma}<S_{n} . $ | (23) |
本章结合中国首个小行星撞击任务,通过数值仿真,验证第2章所提出搜索方案的有效性。
3.1 仿真参数选取本次撞击任务的目标为一颗直径约30 m的近地小行星2020PN1。撞击器计划于2025年8月发射,并于2026年11月达到目标小行星附近,最终撞击器将以5.0 km/s的速度撞击目标小行星。根据相机性能参数,其最远观测距离为20 000.00 km,视场角为0.22 °,分辨率为2 048×2 048,曝光时间为100.0 ms。目标小行星定轨误差最大值为300.00 km,即目标区域为以当前时刻小行星星历位置为球心,半径为300.00 km的球形区域。
仿真开始时刻,相机光轴指向目标区域球心,根据式(2)可知,相机视野在平面β上的投影半径为
| $ r=L \cdot \tan \frac{\alpha}{2}=38.40(\mathrm{~km}) . $ | (24) |
由于撞击器姿态机动存在误差,且视野范围存在变化,为避免覆盖区域出现遗漏,各视野需适当重叠。仿真过程中,相机视野重叠度设为10%,即平面β上视野的有效半径r0=90%r=34.56 km。由式(23)以及r0可计算出所需的搜索层数为5层。
为验证搜索方案的有效性,共进行了1 000次Monte Carlo数值仿真。仿真步长设置为1.0 s。仿真过程中,撞击器与目标小行星均采用日心二体轨道模型。在仿真开始时刻,撞击器与目标小行星星历位置距离为20 000.00 km,相对速度为5.0 km/s,协调世界时(universal time coordinated,UTC)为2026年11月4日17∶10∶05。撞击器与目标小行星在J2000日心黄道坐标系下的初始位置速度如表 1所示。对于每一个仿真算例,撞击器相对于惯性系的三轴初始角速度均设置为零,其初始姿态x轴指向初始时刻目标星历位置,y、z两轴随机选取。撞击器惯量信息以及机动能力如表 2所示。
| 参数 | 取值 |
| 撞击器J2000日心黄道坐标系位置矢量/m | (1.412×1011, 8.981×1010, -1 339.000×1010) |
| 撞击器J2000日心黄道坐标系速度矢量/(m·s-1) | (-1.043×104, 2.413 ×104, -1.420×102) |
| 目标小行星J2000日心黄道坐标系位置矢量/m | (1.412×1011, 8.982 ×1010, - 1 339.000×1010) |
| 目标小行星J2000日心黄道坐标系速度矢量/(m·s-1) | (-1.479×104, 2.178×104, -8.080×102) |
| 参数 | 取值 |
| 撞击器质量/kg | 500 |
| 撞击器惯量diag(A0, B0, C0)/(kg·m2) | diag(25, 50, 50) |
| x轴喷气力矩Mx1,Mx2/(N·m-1) | 6.0,0.6 |
| y轴喷气力矩My1,My2/(N·m-1) | 8.0,0.8 |
| z轴喷气力矩Mz1,Mz2/(N·m-1) | 8.0,0.8 |
| 控制周期/ms | 50.0 |
随机选取目标小行星位置误差方向,位置误差大小在[0,300.00] km范围内均匀分布。在整个搜索过程中,太阳-小行星-撞击器相角始终维持约12°,可见星等约为11,可满足相机成像与识别条件。因此,当目标小行星出现在相机视野区域内时,即认为相机成功捕获目标小行星,此时仿真终止。若5层搜索方案执行结束均未捕获目标,则认为本次搜索任务失败。
3.2 机动方案为完成目标区域搜索,需调整相机光轴指向,使其恰好通过平面β上相应的圆心位置。
由于固连系原点与平面β距离为L,因此,平面β上i号圆心位置(yi, zi)在固连系下的坐标(xi1, yi1, zi1)为
| $ \boldsymbol{v}=\left(x_{i}^{1}, y_{i}^{1}, z_{i}^{1}\right)=\left(L, y_{i}, z_{i}\right) . $ | (25) |
利用喷气控制调整撞击器姿态,使其本体系x轴沿v方向延伸,即可完成相机光轴指向控制。同时,由于相机无法在姿态运动过程中成像,因此在成像过程中,需控制撞击器的角速度相对于惯性的角速度为0。
3.3 仿真结果如图 8a所示,5层搜索方案可完全覆盖目标区域。
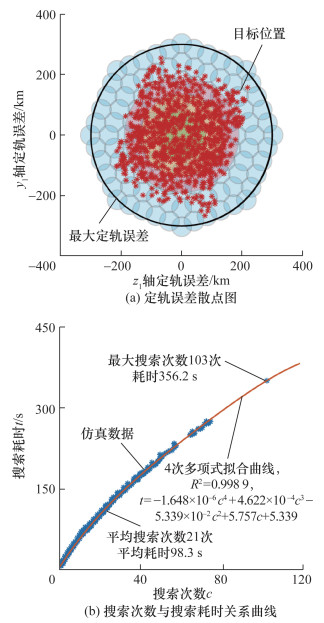
|
| 图 8 定轨误差散点图及搜索次数与搜索耗时关系曲线 |
仿真结果显示,1 000次Monte Carlo仿真均成功捕获目标小行星,即成功率为100%。搜索方案包括撞击器姿态机动、相机成像及图像处理等过程,最大耗时为356.2 s,平均耗时为98.3 s,能够满足本次任务400.0 s的时间限制。1 000次仿真中最大搜索次数为103次,平均搜索次数为21次。图 8b展示了c与t关系曲线。通过4次多项式拟合,计算得到其曲线表达式为
| $ \begin{gathered} t=-1.648 \times 10^{-6} c^{4}+4.622 \times 10^{-4} c^{3}-\\ 5.339 \times 10^{-2} c^{2}+5.757 c+5.339 . \end{gathered} $ | (26) |
通过计算可知,式(26)的一阶导数最小值在c=121时取得,为1.460,即最短搜索耗时约为1.5 s,远高于星载计算机单张图像处理时间0.5 s。5层搜索方案最多搜索121次,利用式(26)可估计其最大搜索耗时为385.9 s,仍满足400.0 s的搜索时间限制。
4 结论本文以中国首个小行星撞击任务为背景,针对定轨误差较大的小直径目标小行星,设计了一种可最大化单次成像面积的目标搜索方案。本文利用几何关系,证明了该方案可通过调整搜索次数覆盖不同面积的目标区域。文中给出了不同搜索次数可覆盖区域面积的解析表达式以及不同视野位置的递推计算方法。通过Monte Carlo数值仿真,验证了方案的有效性,其搜索成功率可达100%,搜索最大耗时为356.2 s,平均耗时为98.3 s,单次搜索最短耗时约为1.5 s,可满足相机性能、星载计算机性能以及机动时间等多方面需求。
| [1] |
ANTHONY N, EMAMI M R. Asteroid engineering: The state-of-the-art of near-Earth asteroids science and technology[J]. Progress in Aerospace Sciences, 2018, 100: 1-17. DOI:10.1016/j.paerosci.2018.05.001 |
| [2] |
CHENG B, ASPHAUG E, YU Y, et al. Measuring the mechanical properties of small body regolith layers using a granular penetrometer[J]. Astrodynamics, 2023, 7(1): 15-29. DOI:10.1007/s42064-021-0127-8 |
| [3] |
CASTILLO-ROGEZ J C, PAVONE M, HOFFMAN J A, et al. Expected science return of spatially-extended in-situ exploration at small Solar system bodies[C]// Proceedings of 2012 IEEE Aerospace Conference. Sky, USA: IEEE, 2012: 1-15.
|
| [4] |
ZHANG Y, MICHEL P. Shapes, structures, and evolution of small bodies[J]. Astrodynamics, 2021, 5(4): 293-329. DOI:10.1007/s42064-021-0128-7 |
| [5] |
ZACNY K, COHEN M M, JAMES W W, et al. Asteroid mining[C]// AIAA SPACE 2013 Conference and Exposition. San Diego, USA: American Institute of Aeronautics and Astronautics, 2013.
|
| [6] |
唐玉华, 吴伟仁, 李明涛, 等. 地月空间近地小行星观测系统研究[J]. 中国科学: 信息科学, 2022, 52(7): 1169-1185. TANG Y H, WU W R, LI M T, et al. Near-Earth asteroids observation system in cislunar space[J]. Scientia Sinica Informationis, 2022, 52(7): 1169-1185. (in Chinese) |
| [7] |
BROWN P G, ASSINK J D, ASTIZ L, et al. A 500-kiloton airburst over Chelyabinsk and an enhanced hazard from small impactors[J]. Nature, 2013, 503(7475): 238-241. DOI:10.1038/nature12741 |
| [8] |
MICHELI M, WAINSCOAT R J, DENNEAU L. Detectability of Chelyabinsk-like impactors with Pan-STARRS[J]. Icarus, 2018, 303: 265-272. DOI:10.1016/j.icarus.2017.10.010 |
| [9] |
JIAO Y F, CHENG B, BAOYIN H X. Optimal kinetic-impact geometry for asteroid deflection exploiting delta-V hodograph[J]. Journal of Guidance, Control, and Dynamics, 2023, 46(2): 382-389. DOI:10.2514/1.G006876 |
| [10] |
BUS S J, BINZEL R P. Phase Ⅱ of the small main-belt asteroid spectroscopic survey: A feature-based taxonomy[J]. Icarus, 2002, 158(1): 146-177. DOI:10.1006/icar.2002.6856 |
| [11] |
WATANABE S, HIRABAYASHI M, HIRATA N, et al. Hayabusa2 arrives at the carbonaceous asteroid 162173 Ryugu: A spinning top-shaped rubble pile[J]. Science, 2019, 364(6437): 268-272. DOI:10.1126/science.aav8032 |
| [12] |
RIVKIN A S, CHABOT N L, STICKLE A M, et al. The double asteroid redirection test (DART): Planetary defense investigations and requirements[J]. The Planetary Science Journal, 2021, 2(5): 173. DOI:10.3847/PSJ/ac063e |
| [13] |
DENG X C, FAN A Q. China marks 7th Space Day amid busy mission schedule[EB/OL]. (2022-04-24)[2023-10-23]. http://en.people.cn/n3/2022/0425/c90000-10088884.html.
|
| [14] |
FEDERICI L, SCORSOGLIO A, GHILARDI L, et al, Image-based meta-reinforcement learning for autonomous terminal guidance of an impactor in a binary asteroid system[C]// AIAA SCITECH 2022 Forum. San Diego, USA: AIAA, 2022: 2270.
|
| [15] |
韩柠, 刘辉, 王云财, 等. 基于比例导引的深空撞击脉冲导引律设计[J]. 动力学与控制学报, 2019, 17(1): 86-90. HAN N, LIU H, WANG Y C, et al. Pulse guidance law for deep space impact based on the proportional guidance[J]. Journal of Dynamics and Control, 2019, 17(1): 86-90. (in Chinese) |
| [16] |
CANO J L, BASTANTE J C. Very small asteroids detection and rendezvous strategy[C]// Proceedings of the 24th International Symposium on Space Flight Dynamics. Laurel, USA: ISSFD, 2014.
|
| [17] |
YU S Y, GAO H D, MA J, et al. Selection of acquisition scan methods in intersatellite optical communications[J]. Chinese Journal of Lasers. B, 2002(5): 364-368. |
| [18] |
冯国柱, 杨华军, 邱琪, 等. 螺旋式扫描在激光雷达系统中的仿真优化分析[J]. 红外与激光工程, 2006, 35(2): 165-168. FENG G Z, YANG H J, QIU Q, et al. Analyzing from simulation of optimizing the spiral scan in the laser radar system[J]. Infrared and Laser Engineering, 2006, 35(2): 165-168. DOI:10.3969/j.issn.1007-2276.2006.02.010 (in Chinese) |
| [19] |
YOU Y, WANG H. Onboard target searching strategy during lost in space situations in angles-only navigation active space debris removal[J]. International Journal of Aeronautical and Space Sciences, 2019, 20(3): 815-829. DOI:10.1007/s42405-019-00163-8 |
| [20] |
HU H L, SHANG J, YANG L, et al. Scan planning optimization for 2-D beam scanning using a future geostationary microwave radiometer[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(5): 3167-3184. DOI:10.1109/TAES.2021.3068440 |
| [21] |
张众, 鄂智博, 黄丽霞, 等. 遥感卫星对区域目标可见窗口的半解析快速算法[J]. 清华大学学报(自然科学版), 2022, 62(3): 573-580. ZHANG Z, E Z B, HUANG L X, et al. Semi-analytical algorithm for computing satellite-area target visibility[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(3): 573-580. (in Chinese) |
| [22] |
鄂智博, 李俊峰. 遥感卫星对区域目标可见性的快速计算方法[J]. 清华大学学报(自然科学版), 2019, 59(9): 699-704. E Z B, LI J F. Fast simulation algorithm for area target visibility using remote sensing satellites[J]. Journal of Tsinghua University (Science and Technology), 2019, 59(9): 699-704. (in Chinese) |
| [23] |
甘岚, 龚胜平. 机动卫星星座对多目标成像任务规划[J]. 清华大学学报(自然科学版), 2021, 61(3): 240-247. GAN L, GONG S P. Observation mission planning for maneuverable satellite constellations towards multiple targets[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(3): 240-247. (in Chinese) |
| [24] |
ZHI Z, QU H S, TAO S P, et al. The design of cone and pendulum scanning mode using dual-camera with multi- dimensional motion imaging micro-nanosatellite[J]. Remote Sensing, 2022, 14(18): 4613. DOI:10.3390/rs14184613 |
| [25] |
宝音贺西, 印明威. 敏捷卫星时间最优姿态机动研究综述[J]. 动力学与控制学报, 2020, 18(4): 1-11. BAOYIN H X, YIN M W. Review on time-optimal reorientation of agile satellites[J]. Journal of Dynamics and Control, 2020, 18(4): 1-11. (in Chinese) |
| [26] |
于龙江, 蒋方华, 姜洋, 等. 敏捷卫星一般轨迹主动推扫成像模式设计[J]. 航天器工程, 2019, 28(1): 27-34. YU L J, JIANG F H, JIANG Y, et al. Design of agile satellite's active scanning imaging mode on general track[J]. Spacecraft Engineering, 2019, 28(1): 27-34. (in Chinese) |
| [27] |
余婧, 喜进军, 于龙江, 等. 敏捷卫星同轨多条带拼幅成像模式研究[J]. 航天器工程, 2015, 24(2): 27-34. YU J, XI J J, YU L J, et al. Study of one-orbit multi-stripes splicing imaging for agile satellite[J]. Spacecraft Engineering, 2015, 24(2): 27-34. (in Chinese) |
| [28] |
章登义, 郭雷, 王骞, 等. 一种面向区域目标的敏捷成像卫星单轨调度方法[J]. 武汉大学学报(信息科学版), 2014, 39(8): 901-905, 922. ZHANG D Y, GUO L, WANG Q, et al. An improved single-orbit scheduling method for agile imaging satellite towards area target[J]. Geomatics and Information Science of Wuhan University, 2014, 39(8): 901-905, 922. (in Chinese) |
| [29] |
张新伟, 戴君, 刘付强. 敏捷遥感卫星工作模式研究[J]. 航天器工程, 2011, 20(4): 32-38. ZHANG X W, DAI J, LIU F Q. Research on working mode of remote sensing satellite with agile attitude control[J]. Spacecraft Engineering, 2011, 20(4): 32-38. (in Chinese) |



