2. 长安大学 运输工程学院, 西安 710064
2. School of Transportation Engineering, Chang'an University, Xi'an 710064, China
近年来,随着城市人口规模的迅速扩张,城市轨道交通网络(urban rail transit network, URTN)客流规模快速增长,轨道站点的运输能力与客运需求之间的供需关系出现失衡[1],引发某些轨道站点或线路失效。由于URTN中各轨道站点之间相互连接,某一站点受突发扰动运行中断后,会导致其他站点和线路因受影响而相继失效,最终导致部分,甚至整个URTN崩溃(即级联失效[2]),反映出URTN的脆弱性特征。因此,提升URTN的抗毁性是URTN正常运行的重要保障。
URTN抗毁性是URTN受突发扰动时的应变能力和适应能力,是URTN脆弱性研究的进一步延伸[3-5]。URTN抗毁性可从维持原有运输效率的结构抗毁性和维持原有客运服务水平的功能抗毁性2个角度进行刻画。国内外学者围绕URTN抗毁性测量方法进行了研究。杨景峰等[6]构建了北京-上海-深圳URTN,通过负载重分配模型对比分析随机攻击和蓄意攻击策略下的URTN抗毁性水平;马书红等[7]通过构建多维度的韧性评估模型计算城市群客运网络的结构韧性水平;Wu等[8]改进可靠性评价指标,建立耦合映像格子(coupled map lattice, CML)模型,研究不同参数下URTN级联失效的规律。同时,部分学者采用多层复合网络进一步探究URTN抗毁性的影响因素。王永岗等[9]通过构建公路、铁路、航空和水运等多层次复合网络,对比不同攻击方式对URTN抗毁性的影响程度;王秋玲等[10]通过构建公交、地铁、自行车3层网络,探究不同网络层、抵抗参数下,URTN抗毁性的变化规律;李成兵等[11]通过构建道路、轨道和航空城市群综合客运网络,剖析抗毁性影响因素。此外,应用模型构建方法探究URTN抗毁性提升路径是当前的研究热点。Lu等[12]通过构建多场景多目标的优化模型,探究URTN抗毁性的提高策略;路庆昌等[13]基于遗传算法和Frank-Wolfe算法提出地铁网络保护决策的优化办法;Huang等[14]基于灾害扩散理论构建考虑多因素的级联失效动态评价模型,并提出应急策略;冯树民等[15]基于解释结构模型探究URTN抗毁性的影响因素,提出拓扑结构和客流量状况是URTN抗毁性最直接的影响因素。
综上所述,现有研究大多从轨道交通系统的拓扑结构出发,选用最大连通子图[16]、网络效率[17]、有效节点比[18]等拓扑指标,对URTN的抗毁性水平进行评估。这些研究为进一步完善城市轨道交通抗毁性研究方法、识别抗毁性影响因素和评估抗毁性作出了重要贡献。实际上,URTN是由基础设施、运营管理系统和乘客共同构成的具有时空特征的复杂系统,客流是评估URTN的结构和功能抗毁性水平的重要因素。因此,有必要从客流变化角度(尤其是大客流)分析URTN的运行状态。在自然灾害、突发事件和大型活动等背景下,大量乘客易在短时间内聚集,出现大客流拥挤现象。大客流拥挤现象指单位时间内轨道站点客流量接近,甚至大于额定承载量,且有继续增加的趋势[15],伴随明显的乘客出行需求和列车运输供给能力非均衡特征。URTN中人流密集且空间相对封闭,非均衡大客流会增大站内拥挤事件的发生频率和传播范围,造成站点失效,这不仅影响乘客出行效率,降低城市轨道交通运营的服务质量,还为轨道交通运营和乘客带来极大的安全隐患[19]。
基于此,本文考虑非均衡大客流冲击情景,深入分析非均衡大客流对URTN级联失效的影响机理,并根据非均衡大客流时段各轨道站点单位时间内的客流量构建客流加权URTN,结合各轨道站点的拓扑结构特征和客流分布情况识别关键轨道站点。此外,本文利用故障节点比和网络强度熵指标动态评估URTN的结构抗毁性和功能抗毁性水平,并分析其演化规律,为非均衡大客流冲击下城市轨道交通的安全运营管理提供决策依据。
1 非均衡大客流对城市轨道交通网络级联失效的影响受有限时空范围和轨道站点容量的限制,使用轨道交通出行的乘客短时增多,导致某些轨道站点的运输能力不能满足乘客的出行需求,造成站内大量乘客聚集,滞留在站台等候区、扶梯、水平走行区等区域,形成大客流拥挤现象。非均衡大客流具有时空分布不均衡特征,易造成站内客流拥挤,进而导致乘客流动速度减缓,乘客密度增大,影响URTN的客运服务水平,甚至引发踩踏、车门夹人事件等安全事故,造成列车延迟、乘客候车时间增加,降低URTN的运输效率。由于各轨道站点相互连接,因此,相邻站点间的客流拥挤具有传播性,会加剧URTN级联失效传播。
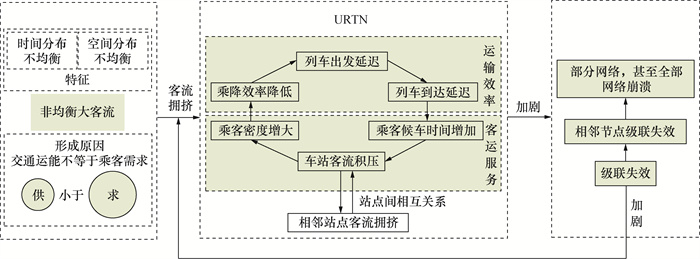
非均衡大客流冲击加剧URTN的运营风险,增加URTN级联失效的发生概率。因此,需要从抗毁性视角,基于轨道站点客流分布情况构建URTN级联失效模型,分析非均衡大客流冲击下URTN的结构和功能抗毁性演化规律。在城市交通早高峰时段,非均衡大客流规模大、时效强,是URTN运营中需要面对的关键难题。因此,本文主要探究早高峰时段大客流冲击下的URTN抗毁性演化规律。非均衡大客流对URTN级联失效的影响机理如图 1所示。
|
| 图 1 非均衡大客流对URTN级联失效的影响机理 |
2 非均衡大客流下城市轨道交通网络拓扑结构 2.1 客流加权网络构建
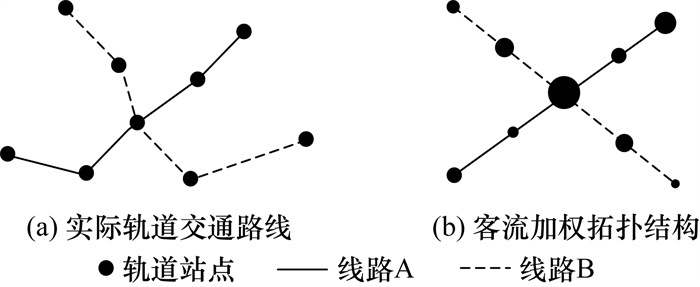
URTN具有动态客流性,且非均衡大客流时空分布不均衡特征明显[20]。构建客流加权网络有助于深入分析城市轨道交通客流的时空分布,从而更真实地模拟考虑客流选择行为的URTN抗毁性演化过程。利用研究时段内各轨道站点单位时间内的客流量构建客流加权URTN,可同时反映URTN拓扑结构和客流分布情况。Space L拓扑结构构建方法将轨道站点抽象为节点,将轨道站点间相连的线路抽象为连边,能直观反映URTN中各站点的相互连接关系,故本文利用Space L方法构建URTN拓扑结构模型,即
|
| 图 2 客流加权URTN构建 |
2.2 城市轨道交通网络的关键站点识别
URTN中的不同轨道站点因其所属线路、拓扑特征不同而重要程度不同。通过评估轨道站点的重要程度识别关键站点,分析关键站点受扰动后引发URTN级联失效过程中结构抗毁水平和功能抗毁水平的演化规律,并采取相应的管理和维护措施,优化城市轨道交通的应急预案,是保障非均衡大客流冲击下URTN安全运营的基础。轨道站点客流量是衡量URTN站点关键性的重要指标[24]。本文结合URTN拓扑结构特征和客流分布特征,选用节点度数、节点介数和客流强度指标,分别识别URTN中节点度数最大、节点介数最大和客流强度最大的轨道站点,据此研究不同特征的关键站点引发URTN级联失效的演化规律。
2.2.1 节点度数节点度数Ki指与轨道站点i直接相连的轨道站点或连边个数,是识别关键站点的重要指标[25],表示如下:
| $ K_i=\sum\limits_{j=1}^N a_{i j}. $ | (1) |
节点度数越大,该轨道站点越重要。不同节点度数的轨道站点受突发扰动后,因邻边数量不同,级联失效传播的范围和速度也不同。
2.2.2 节点介数节点介数Bi指经过轨道站点i的最短路径数占所有最短路径数的比例[22],该轨道站点在URTN结构中的重要程度可量化,表示如下:
| $ B_i=\sum\limits_{j \neq l \neq i}\left[\frac{\sigma_{j l}(i)}{\sigma_{j l}}\right]. $ | (2) |
其中:σjl(i)为轨道站点j—l的最短路径中,经过轨道站点i的最短路径数;σjl为轨道站点j—l之间的最短路径总数。在URTN中,轨道站点的节点介数越大,说明该轨道站点连接的最短路径越多,运输和中转的乘客越多。
2.2.3 客流强度在客流加权URTN中,轨道站点的客流强度常被认为是轨道站点负载客流量的典型指标[3, 24]。本文定义客流强度Si为轨道站点i早高峰时段单位时间内的客流量,即进站客流量、出站客流量的和[22-23],可反映轨道站点在满足局部出行需求方面发挥的作用,如式(3)所示。
| $ S_i=Q_{\text {in }}(i)+Q_{\text {out }}(i) $ | (3) |
其中:Qin(i)为轨道站点i在单位时间内的进站客流量;Qout(i)为轨道站点i在单位时间内的出站客流量。轨道站点客流强度可用于衡量URTN中的非均衡大客流分布情况,并可用于识别人口密集、出行需求相对较大的关键站点。
3 城市轨道交通网络级联失效抗毁性模型 3.1 轨道交通网络突发扰动等级URTN突发扰动指对URTN有序运行产生威胁,并导致URTN的轨道站点或线路受到破坏的突发事件。根据URTN突发扰动的成因、性质和表现形式,可分为洪涝、地震等自然灾害扰动,火灾、恐怖袭击等社会安全扰动,重大传染病、群体性不明原因疾病等公共卫生扰动,信号故障、供电故障等设备设施扰动,以及乘客安全事故、突发疾病等客运类扰动。不同突发扰动造成的URTN级联失效规模和传播范围不同。定义URTN突发扰动R∈(0, +∞),R值越大,突发扰动的破坏程度越大,影响范围越广。参照《国家城市轨道交通运营突发事件应急预案》[26],结合国内外地铁事故案例,将R按破坏程度和影响范围划分为特别重大扰动、重大扰动、较大扰动、一般扰动、险性扰动5个等级[27]。由于R等级指标为定性指标,因此可利用模糊综合评价法界定扰动等级[28]。借鉴Shen等[29]的界定范围和杨阳等[30]的划分标准,将5个突发扰动等级均等划分至区间(0, 10)内[31],具体等级界定标准及取值如表 1所示。
| 扰动等级 | 扰动内涵 | 取值 |
| 特别重大扰动 | Ⅰ级恶劣天气(暴雨、暴雪、台风等极端天气)、7级以上地震(人口密集地区)或7.5级以上地震(其他地区)、特别重大安全事故等 | [8, 10) |
| 重大扰动 | Ⅱ级恶劣天气(暴雨、暴雪、台风等极端天气)、6.0~6.9级地震(人口密集地区)或6.5~7.4级地震(其他地区)、重大安全事故等 | [6, 8) |
| 较大扰动 | Ⅲ级恶劣天气(暴雨、暴雪、台风等极端天气)、5.0~5.9级地震(人口密集地区)或5.5~6.4级地震(其他地区)、较大安全事故等 | [4, 6) |
| 一般扰动 | Ⅳ级恶劣天气(暴雨、暴雪、台风等极端天气)、4.0~4.9级地震(人口密集地区)或4.5~5.4级地震(其他地区)、一般安全事故等 | [2, 4) |
| 险性扰动 | 4.0级以下地震(人口密集地区)或4.5级以下地震(其他地区)、险性安全事故等 | (0, 2) |
3.2 模型构建与参数设置
在URTN级联失效过程中,URTN抗毁性水平随时间变化,且通过连边的耦合作用相互影响,即网络中轨道站点与连边之间存在彼此关联、相互作用的关系。CML模型将时间和空间变量离散化,将状态变量保持连续,这能从本质上反映系统的复杂时空特性,广泛用于城市道路网络、电力网络等级联失效动力学行为研究。
现有研究通常在(0, 1)范围内随机生成网络节点的初始状态值[10, 29]。然而,在CML模型中,初始状态值具有敏感依赖性,随连续迭代次数的不断增加,节点初始状态值的误差急剧增大。因此,为提高节点状态预测的精准度,本文设计了一种改进的CML算法,用于反映轨道站点间的耦合作用机制,即当前时刻轨道站点状态值与上一时刻轨道站点状态值、相邻轨道站点状态值之间的相互作用关系,表示如下:
| $ \left\{\begin{array}{c} x_i(t+1)=\mid(1-\varepsilon) f\left(x_i(t)\right)+ \\ \left.\varepsilon \sum\limits_{j=1, j \neq i}^N a_{i j} \frac{f\left(x_j(t)\right)}{K_i} \right\rvert\, ,\\ x_i\left(t_0\right)=S_i\left(t_0\right) / C_i\left(t_0\right). \end{array}\right. $ | (4) |
其中:轨道站点i的客流饱和程度xi(t0)为初始状态值,即单位时间内的客流量与额定负载量的比值[32];Si(t0)为轨道站点i在t0时刻的客流量;Ci(t0)为轨道站点i在t0时刻的额定负载容量。分析不同轨道站点在不同时间的状态值,判断轨道站点所处的状态(正常、拥堵或失效)。若0<xi(t)<1,则轨道站点i处于正常运行状态;若xi(t)≥1,则该轨道站点i处于拥堵或失效状态; xi(t)和xi(t+1)分别为轨道站点i在t时刻、t+1时刻的状态值;t表示时间步长,即故障传播下轨道站点状态值迭代次数;aij为轨道站点间的连接信息;ε为相邻轨道站点间的耦合系数,即相邻轨道站点间的相互影响程度,可反映轨道站点状态对相邻轨道站点状态的作用强度,ε∈[0, 1],ε越大,相邻轨道站点间的相互作用关系越强;f(x)为混沌Logistic映射函数,表征轨道站点或线路容量约束的演化规律,本文利用f(x)=4x(1-x)[12, 24, 33]描述URTN中轨道站点的动态行为。当0≤x≤1时,0≤f(x)≤1。
设tq时刻轨道站点i的状态值为xi(tq)。当t=tq+1时,轨道站点i受到突发扰动R,如图 3a所示,可表示如下:
| $ \begin{gathered} x_i\left(t_{q+1}\right)=\mid(1-\varepsilon) f\left(x_i\left(t_q\right)\right)+ \\ \left.\varepsilon \sum\limits_{j=1, j \neq i}^N a_{i j} \frac{f\left(x_j\left(t_q\right)\right)}{K_i} \right\rvert\,+R . \end{gathered} $ | (5) |
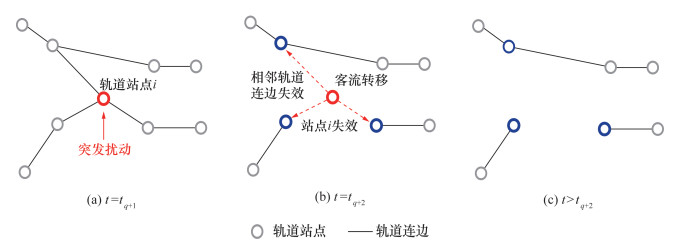
在轨道站点i受到突发扰动R后,若xi(tq+1)≥1,则轨道站点i中负载的乘客超过其额定容量,轨道站点i在t=tq+1时发生故障,此后,轨道站点i失效,乘客容量变为0,即当t>tq+1时,xi(t)≡0;当t=tq+2时,失效轨道站点i通过连边耦合关系向相邻轨道站点进行客流转移,由式(4)计算xi(tq+1),客流转移如图 3b所示。若xi(tq+2)≤1,则URTN级联失效中止,如图 3c所示;若xi(tq+2)>1,则引起新一轮的轨道站点故障,并进行客流转移,直至故障轨道站点累积总数不再增加。
|
| 图 3 级联失效客流转移示意图 |
为研究相邻轨道站点间的ε对URTN级联失效抗毁性演化规律的影响程度,本文参照文[34]将相邻轨道站点间的ε取值设为0.1~0.9,具体的参数描述如表 2所示。
| 编号 | ε | 参数描述 |
| 1 | 0.1 | 轨道站点10%的状态变化源于相邻轨道站点的客流转移 |
| 2 | 0.2 | 轨道站点20%的状态变化源于相邻轨道站点的客流转移 |
| 3 | 0.3 | 轨道站点30%的状态变化源于相邻轨道站点的客流转移 |
| 4 | 0.4 | 轨道站点40%的状态变化源于相邻轨道站点的客流转移 |
| 5 | 0.5 | 轨道站点50%的状态变化源于相邻轨道站点的客流转移 |
| 6 | 0.6 | 轨道站点60%的状态变化源于相邻轨道站点的客流转移 |
| 7 | 0.7 | 轨道站点70%的状态变化源于相邻轨道站点的客流转移 |
| 8 | 0.8 | 轨道站点80%的状态变化源于相邻轨道站点的客流转移 |
| 9 | 0.9 | 轨道站点90%的状态变化源于相邻轨道站点的客流转移 |
3.3 城市轨道交通网络抗毁性评价指标 3.3.1 故障节点比
故障节点比I(t)指t时刻URTN中失效轨道站点总数与轨道站点总数的比值[34],用以评估URTN的结构抗毁性水平,表示如下:
| $ I(t)=N_t / N $ | (6) |
其中Nt为t时刻URTN受突发扰动后故障轨道站点的累积总数。
I(t)∈[0, 1],I(t)值越大,URTN中的故障轨道站点越多,URTN的结构抗毁性越弱;反之,URTN的结构抗毁性越强。
3.3.2 网络强度熵为量化非均衡大客流对URTN客流服务和运营管理功能的影响程度,本文利用网络强度熵衡量功能抗毁性水平的演化特征。熵是一种度量系统无序程度的指标,网络强度熵G(t)通过引入轨道站点客流权重测量URTN中客流分布的均匀程度[8],反映URTN中客流适应外界变化的能力(即功能抗毁性),表示如下:
| $ \left\{\begin{array}{l} G(t)=-\sum\limits_{i=1}^N w_i \ln w_i, \\ w_i=S_i / \sum\limits_{i=1}^N S_i. \end{array}\right. $ | (7) |
当URTN中客流适应外界变化时,客流分布均匀,wi=1/N,此时,网络强度熵取最大值, Gmax(t)=lnN;当URTN中客流集中于站点i时,wi=1, wj=0(j≠i),此时,网络强度熵取最小值, Gmin(t)=0。G(t)值越大,URTN适应外界变化的能力越强,功能抗毁性越强;反之,功能抗毁性越弱。当G(t)=0时,URTN的功能抗毁性失效。为消除URTN中轨道站点数量N的影响,对网络强度熵G(t)进行归一化处理,如式(8)所示,Gs(t)为标准网络强度熵。
| $ \begin{gathered} G_{\mathrm{s}}(t)=\frac{G(t)-G_{\min }(t)}{G_{\max }(t)-G_{\min }(t)}=\frac{-\sum\limits_{i=1}^N w_i \ln w_i}{\ln N}= \\ -\sum\limits_{i=1}^N w_i \log _N w_i. \end{gathered} $ | (8) |
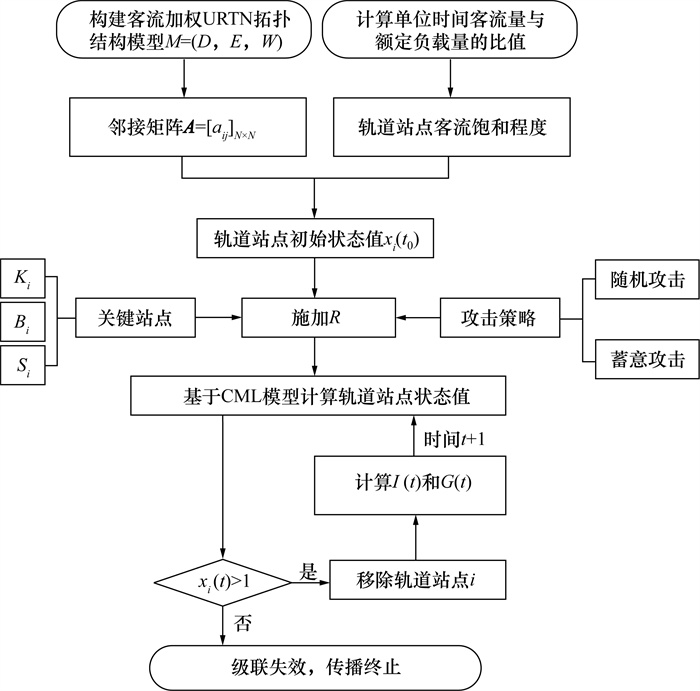
为揭示非均衡大客流冲击下URTN的抗毁性演化特征,本文结合级联失效理论和混沌动力学,开发了一种改进的CML模型算法:通过建立客流加权URTN分析网络拓扑结构和客流分布特征;通过设置轨道站点客流饱和程度为初始状态值提高节点状态预测的精准度;通过设置结构和功能抗毁性评价指标衡量非均衡大客流下URTN的运输效率和客运服务水平。首先根据客流加权URTN生成邻接矩阵,并识别关键站点;其次设置各轨道站点的初始状态值;最后基于关键站点和攻击策略对轨道站点施加扰动,并研究不同特征的关键站点抗毁性演化过程,算法求解流程如图 4所示。
|
| 图 4 URTN级联失效抗毁性算法的求解流程 |
1) 基于复杂网络理论,构建客流加权URTN的拓扑结构模型M=(D, E, W)。
2) 生成邻接矩阵A =[aij]N×N,计算轨道站点的Ki、Bi、Si,并识别关键站点。
3) 设轨道站点的客流饱和度为初始状态值xi(t0),并设置URTN中所有轨道站点的初始状态值处于正常状态,即xi(t0)∈(0, 1)。
4) 基于关键站点采取相应的随机攻击或蓄意攻击策略,即对轨道站点i施加突发扰动R,根据式(5)计算xi(t),并根据式(4)计算其余轨道站点的状态值。若xi(t)≥1,则轨道站点i受突发扰动失效,移除该站点,并记录当前时间的G(t)和I(t)。
5) 根据式(4)更新剩余轨道站点的状态值xi(t+1),并记录当前时间的网络强度熵G(t+1)和故障节点比I(t+1)。
6) 重复步骤5,若xi(t+1)≤1,则URTN的级联失效传播终止。
4 城市轨道交通网络抗毁性演化在URTN级联失效过程中,随着失效轨道站点的客流转移和失效范围的不断扩大,URTN的结构和功能抗毁性水平呈动态演化趋势。本文通过理论解析和数值模拟,基于不同特征的关键站点,构建非均衡大客流冲击下URTN级联失效的抗毁性测量模型,研究故障传播因素和客流强度因素对URTN结构抗毁性和功能抗毁性动态演化过程的影响机理,揭示故障传播的影响因素和客流强度因素与URTN的结构抗毁性和功能抗毁性之间的关系。
4.1 结构抗毁性演化结构抗毁性指在URTN级联失效过程中,URTN所具有的保持轨道站点连通、维持原有运输效率水平等保障轨道网络结构完整的能力。结构抗毁性演化分析主要研究非均衡大客流冲击下,URTN的结构抗毁性水平随时间变化的演化规律。I(t)为URTN的轨道站点失效规模随时间变化的趋势,可反映URTN的结构抗毁性演化规律。本文基于早高峰大客流时段轨道站点客流分布数据,引入I(t),剖析故障传播因素(ε、R) 和客流强度因素对URTN结构抗毁性的影响机理。
4.2 功能抗毁性演化功能抗毁性指在URTN级联失效过程中,URTN维持原有客运服务水平的能力,包括保障乘客进出站效率的能力,维护乘客候车秩序的能力等。功能抗毁性演化分析通过设置不同故障传播因素(ε、R)和客流强度因素研究非均衡大客流冲击下,URTN功能抗毁性水平随时间变化的演化规律,如表 3所示。G(t)为URTN随时间变化适应外界变化能力的趋势,可衡量URTN的功能抗毁性演化规律。
| 抗毁性 | 衡量指标 | 故障传播因素 | 客流强度因素 | |
| ε (0.1~0.9) |
R (1~9) |
|||
| URTN的结构抗毁水平 | I(t) |
度数最大的轨道站点 | 客流强度最大的轨道站点 | |
| 介数最大的轨道站点 | 客流强度较大的轨道站点 | |||
| URTN的功能抗毁水平 | G(t) | 客流强度最大的轨道站点 | 客流强度一般的轨道站点 | |
5 实例分析 5.1 轨道交通网络拓扑结构
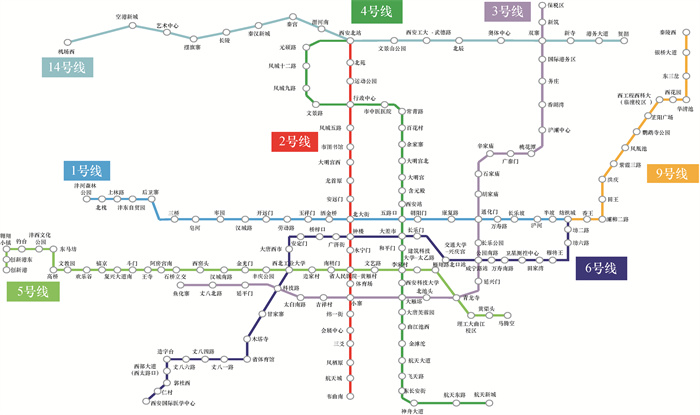
目前,西安市轨道交通已开通8条线路,呈“放射加棋盘”布局,总长为272.4 km,已形成规模化运营网络(见图 5)。2022年西安市轨道交通日均承担客运量210.63万人次,年客运总量排名全国第9。本文以西安市URTN为研究对象,评估早高峰时段非均衡大客流冲击下,URTN受自然灾害、设备故障等突发扰动后,抗毁性水平的演化规律。本研究的线路分布信息来源于西安市轨道交通集团官网,客流数据来源于西安市交通信息中心。基于西安市轨道交通网络的布局,利用Space L方法构建URTN拓扑结构模型。在西安市的URTN拓扑结构中,站点共173个,连边共367条。其中,中转换乘站点18个,平均度为2.121(即每个站点平均与2.121个其他站点直接相连),网络直径为46(即任意可连通的2站点间最长路径长度为46个站点),任意2站点间的平均路径长度为15.04个站点,这表明站点间连通性较好。
|
| 图 5 西安市轨道交通线路图 |
将西安市URTN中的站点度和累积度分布概率在双对数坐标系中进行拟合,得到累积度分布概率函数p(k)=2.237 1k-2.876,幂律指数γ=2.876。根据Albert等[35]对网络拓扑特征的研究,当幂律指数γ∈[2.1, 4.0]时,网络为无标度网络,因此,西安市URTN为无标度网络,具有异质性关键站点,即不同站点在西安市URTN中表现特征不同。
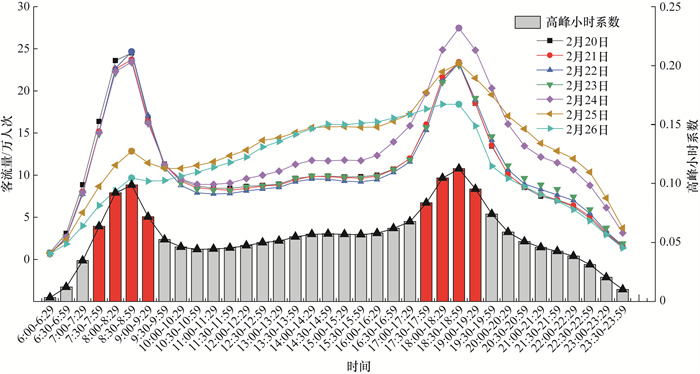
5.2 城市轨道交通网络大客流时空分布特征为反映一般工作日的轨道交通客流分布情况,本文选取2023年2月20日—26日西安市轨道交通车站自动售检票系统(automatic fare collection, AFC)进出站刷卡数据,以30 min为时间间隔,统计连续7 d内西安市轨道交通网络中各时间段内的客流量情况,如图 6所示。通过高峰小时系数(单位小时内客流量占全日客流量的比)识别高峰客流时段,反映轨道交通客流的集中程度。同时,利用时间不均衡系数(运营时间内最大单位小时客流量与全日单位小时平均客流量之比)、空间不均衡系数(轨道站点最大客流量与所有轨道站点平均客流量之比)分别衡量时间、空间分布不均衡程度。不均衡系数越大,不均衡程度越大,客流分布差异越明显。
|
| 图 6 西安市轨道交通客流量分布和高峰小时系数分布(2023年) |
由图 6可知,运营时间内,各时间序列的客流量分布不均衡。2023年2月20日—26日,不均衡系数均大于1(如表 4所示),这表明客流量在时间分布上差异较大。结合图 6中各时间序列内高峰小时系数,判断2023年2月20日—26日西安轨道交通早高峰时段为7:30—9:29,晚高峰时段为17:30—19:29。本文以上述早高峰时段为非均衡大客流研究场景。
| 日期 | 2月20日 | 2月21日 | 2月22日 | 2月23日 | 2月24日 | 2月25日 | 2月26日 |
| 时间不均衡系数 | 2.26 | 2.22 | 2.32 | 2.16 | 2.12 | 1.76 | 1.70 |
| 空间不均衡系数 | 3.19 | 3.22 | 3.16 | 3.24 | 3.11 | 5.21 | 5.56 |
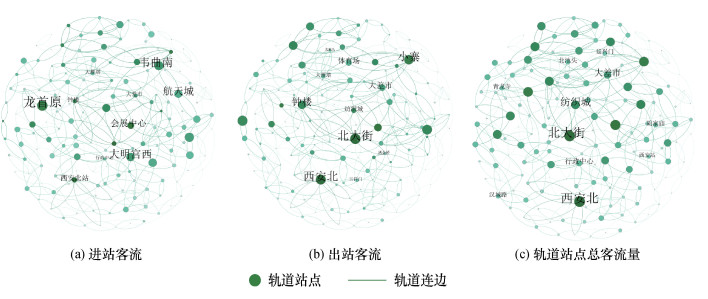
根据2023年2月20日—26日各轨道站点的进站客流量、出站客流量、总客流量的日均值,绘制西安市轨道交通网络客流的空间分布图(如图 7所示)。在图 7中,节点颜色的深浅和大小反映该轨道站点的客流量大小,颜色越深、节点越大,该站点的客流量越大。由图 7可知,客流量空间分布不均衡。结合表 4空间不均衡系数均大于3的研究结果,验证得到各轨道站点客流在空间分布上差异较大。综上所述,西安URTN客流时空分布不均衡特征明显。
|
| 图 7 轨道站点的客流量空间分布 |
5.3 客流加权轨道交通网络构建与关键站点识别
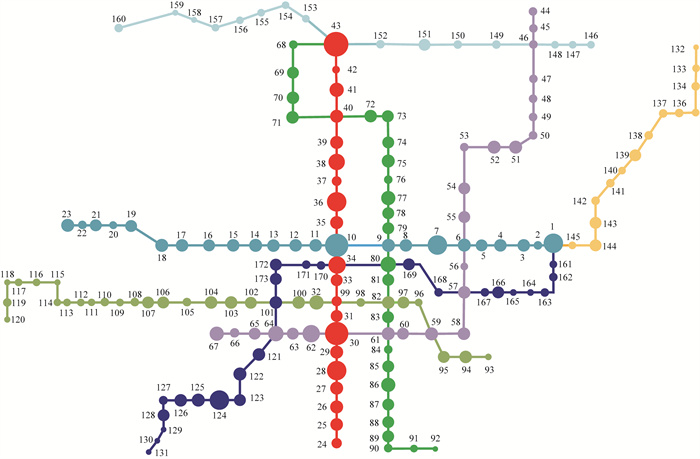
本文为进一步研究早高峰大客流下城市轨道交通客流的时空分布特征,建立客流加权轨道交通网络。首先进行数据预处理,删除同一卡号出现奇数次、刷卡时间间隔过长等异常数据,并筛选出2023年2月20日—26日早高峰时段7:30—9:29内的进出站刷卡数据,包括刷卡卡号、日期、时间、刷卡站点、站点所属线路等;其次遵循先进站后出站的时间顺序,依据卡号提取出行数据的进出站站点和时间,得到进出站客流数列;再次按行程起讫点匹配至各轨道站点,得到2023年2月20日—26日各轨道站点早高峰时段的进站客流量、出站客流量、总客流量;最后对各轨道站点连续7 d早高峰时段的单位时间客流量取均值,构建西安市轨道交通客流加权网络,如图 8所示。图中数字为轨道站点编号,轨道站点符号大小与该轨道站点早高峰时段单位时间内的客流量呈正相关。由此可见:在早高峰时段,西安URTN各轨道站点的客流较大,且存在明显的空间分布差异。
|
| 图 8 西安市客流加权轨道交通网络拓扑图 |
基于西安URTN拓扑结构和早高峰时段单位时间内的客流量数据,利用式(1)—(3)计算西安URTN中各轨道站点的节点度数、节点介数、客流强度,各指标排序前10的轨道站点编号及名称如表 5所示,分别选取节点度数、节点介数、客流强度最大的轨道站点,得到大差市站(K80=5)、北大街站(B10=0.375)、西安北站(S43=7 010)这3个特征明显的关键站点。
| 排序 | 站点编号及名称 | Ki | 站点编号及名称 | Bi | 站点编号及名称 | Si/(人次·h-1) | ||
| 1 | 80大差市站 | 5 | 10北大街站 | 0.375 | 43西安北站 | 7 010 | ||
| 2 | 6通化门站 | 4 | 34钟楼站 | 0.354 | 10北大街站 | 6 725 | ||
| 3 | 7康复路站 | 4 | 6通化门站 | 0.345 | 28会展中心站 | 6 207 | ||
| 4 | 9五路口站 | 4 | 101西北工业大学站 | 0.285 | 36龙首原站 | 6 093 | ||
| 5 | 10北大街站 | 4 | 7康复路站 | 0.254 | 30小寨站 | 5 943 | ||
| 6 | 30小寨站 | 4 | 35安远门站 | 0.210 | 1纺织城站 | 5 716 | ||
| 7 | 34钟楼站 | 4 | 36龙首原站 | 0.203 | 7康复路站 | 5 580 | ||
| 8 | 40行政中心站 | 4 | 80大差市站 | 0.202 | 34钟楼站 | 5 529 | ||
| 9 | 61大雁塔站 | 4 | 64科技路站 | 0.200 | 62吉祥村站 | 5 483 | ||
| 10 | 101西北工业大学站 | 4 | 61大雁塔站 | 0.197 | 38市图书馆站 | 5 473 |
5.4 城市轨道交通网络抗毁性数值模拟
由5.1节分析可知,西安URTN为无标度网络,在受到随机攻击时,抗毁性较强,而在受到蓄意攻击时,抗毁性较弱。因此,为研究URTN抗毁性水平演化规律,选择蓄意攻击策略。同时,轨道站点失效会在较短时间内引发较大范围的级联失效,所以仅考虑轨道站点失效引发的级联失效过程。综上所述,针对大差市站、北大街站和西安北站等异质性关键站点,探究不同故障传播因素(耦合系数ε和突发扰动R)和不同客流强度下URTN级联失效的结构抗毁性水平和功能抗毁性水平的演化规律。
5.4.1 故障传播因素对城市轨道交通网络抗毁性的影响选取节点度数最大的轨道站点大差市站(K80=5)、介数最大的轨道站点北大街站(B10=0.375)和客流强度最大的轨道站点西安北站(S43=7 010) 3个异质性关键站点,模拟早高峰时段非均衡大客流冲击下,ε、R对URTN抗毁性水平的影响。
1) 耦合系数ε对URTN抗毁性的影响。
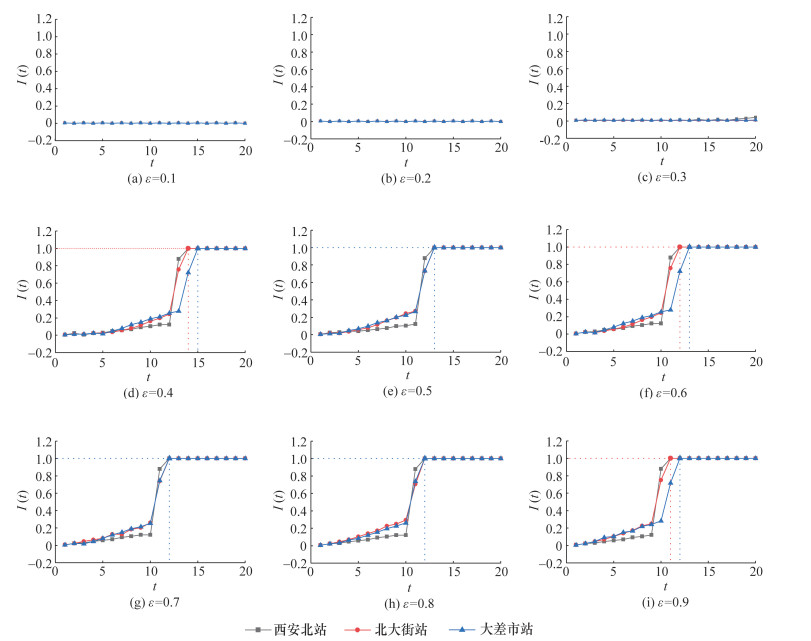
在相邻轨道站点间相互影响程度依次增加的情况下,为剖析URTN级联失效抗毁性水平的演化规律,设相邻轨道站点间相互影响程度为10%~90%,即ε为0.1~0.9。同时,为避免突发扰动因素干扰,设定一般扰动R=2。模拟分析发现,在早高峰时段非均衡大客流冲击下,大差市站、北大街站、西安北站受到一般扰动后,不同ε设置下,URTN的结构抗毁性演化规律如图 9所示。
|
| 图 9 不同轨道站点不同ε下的URTN故障节点比演化规律 |
由图 9可知,URTN的级联失效存在ε临界值。当ε < 0.3时,URTN的故障节点比始终小于1,在任意时间内均不会引起URTN的全局故障,URTN的结构抗毁性水平较高;当ε>0.3时,出现URTN的故障节点比为1的情况,即故障轨道站点通过相邻轨道站点间的相互作用关系,导致相邻轨道站点失效,最终造成全局故障,此时,结构抗毁性失效。同时,当西安北站、北大街站和大差市站这3个关键站点分别受到一般扰动时,若ε=0.5,则3个轨道站点同时在t=13时引发URTN结构抗毁性失效,即t西安北=t北大街=t大差市=13;若ε=0.7,则3个轨道站点同时在t=12时引发URTN结构抗毁性失效,即t西安北=t北大街=t大差市=12。由此可见,URTN中的ε越大,轨道站点受扰动引发URTN全局故障的时间越短。当ε=0.4时,西安北站和北大街站在受到一般扰动后,URTN的结构抗毁性失效时间为t=14,即t西安北=t北大街=14;大差市站在受到一般扰动后,URTN的结构抗毁性失效时间为t=15,即t大差市=15。当ε=0.6时,西安北站和北大街站在受到一般扰动后,URTN的结构抗毁性失效时间为t=12,即t西安北=t北大街=12;大差市站在受到一般扰动后,URTN的结构抗毁性失效时间为t=13,即t大差市=13。由此可见,在非均衡大客流冲击下,与节点度数大的轨道站点相比,节点介数大的轨道站点和客流强度大的轨道站点在受到突发扰动后更易引发URTN的级联失效现象,此时,URTN的结构抗毁性水平更低。
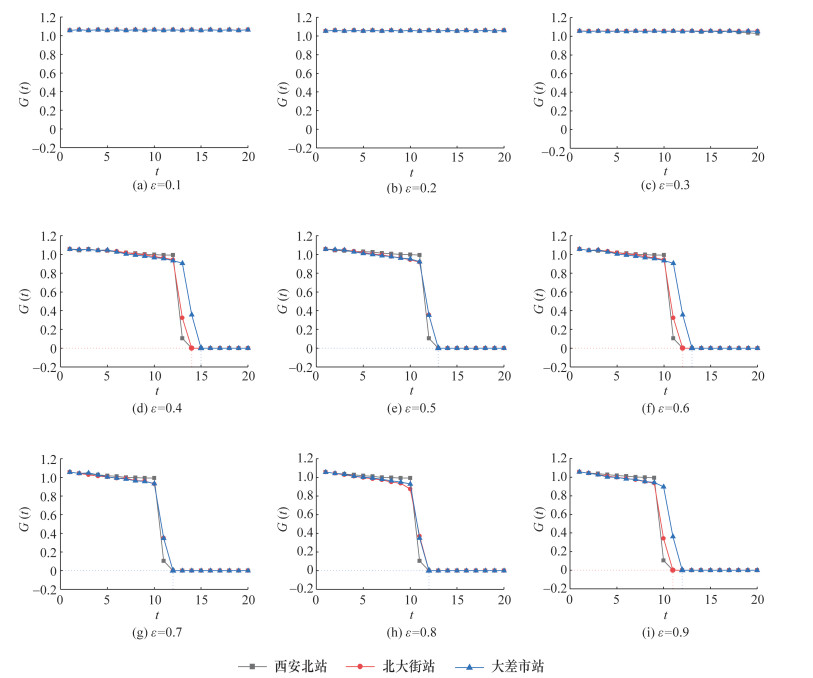
在URTN的级联失效过程中,网络强度熵G(t)呈不断下降趋势,表明URTN的功能抗毁性水平不断降低,如图 10所示。以西安北站为例,当ε=0.4时,URTN的故障节点比在t=14时达到1,即I(14)=1;URTN的网络强度熵在t=14时降为0,即G(14)=0,此时,URTN同时失去运输乘客功能和客运服务功能。由此可见,在URTN的级联失效过程中,功能抗毁性水平和结构抗毁性水平具有相似的演化趋势。
|
| 图 10 不同轨道站点不同ε下的URTN的网络强度熵演化规律 |
综上所述,轨道站点间的相互影响程度越大,级联失效在网络中的传播规模越大,且传播速度越快,URTN的结构抗毁性和功能抗毁性失效时间越短。因此,降低URTN中站点间的耦合系数可有效减小URTN级联失效的传播速度和规模,提高URTN的结构抗毁性和功能抗毁性水平。
2) 突发扰动R对URTN抗毁性的影响。
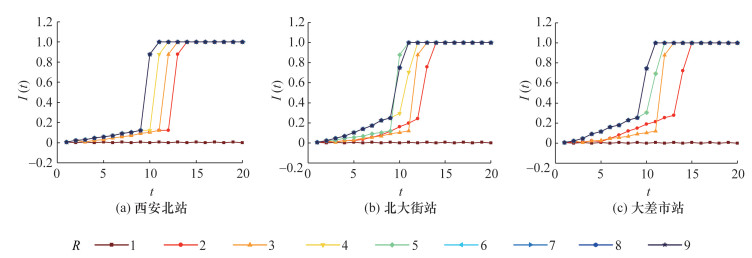
为分析URTN抗毁性水平随突发扰动依次增大的演化规律,分别设置险性扰动R=1;一般扰动R=2,3;较大扰动R=4,5;重大扰动R=6,7;特别重大扰动R=8,9。同时,为避免轨道站点间相互影响程度的干扰,设定耦合系数ε=0.4。早高峰时段,在非均衡大客流冲击下,西安北站、北大街站、大差市站在受到不同程度的突发扰动后,URTN的结构抗毁性演化规律如图 11所示。
|
| 图 11 不同轨道站点不同R下的URTN故障节点比演化规律 |
在不同突发扰动R下,西安北站、北大街站、大差市站引发的级联失效传播范围和传播速度均有相似的变化趋势,但同一轨道站点在受到不同突发扰动R时,URTN的抗毁性演化规律有所不同。在URTN的级联失效过程中,URTN存在突发扰动临界值,即R=1。当站点受到的险性扰动R=1时,不会引发URTN级联失效现象;当突发扰动R>1时,URTN中会出现级联失效现象。同时,随着突发扰动R的增大,URTN中的故障节点比达到1的时间缩短,即URTN的结构抗毁性水平失效时间缩短。当站点受到重大扰动(R=6,7)和特别重大扰动(R=8,9)时,URTN的抗毁性演化规律相同。
当西安北站、北大街站、大差市站受到一般扰动(R=2)时,URTN的故障节点比分别在t=14、t=14、t=15时达到1,即t西安北=t北大街=14,t大差市=15。因此,与节点度数大的轨道站点相比,客流强度大的轨道站点和节点介数大的轨道站点在受到扰动后更易引发URTN级联失效,此时,URTN的结构抗毁性水平更低。
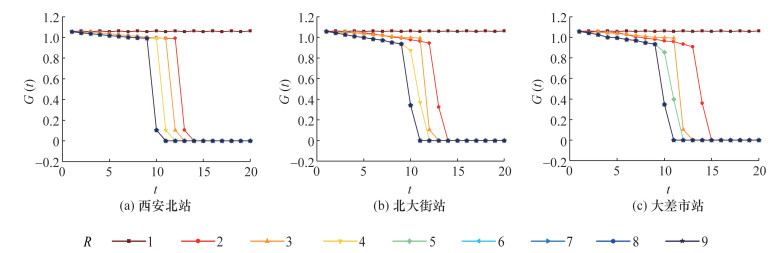
URTN的网络强度熵演化规律如图 12所示。可以看出,随突发扰动增大,同一轨道站点的网络强度熵降为0的时间缩短,URTN的功能抗毁性水平降低。以北大街站为例,当受到一般扰动R=3时,URTN的故障节点比和网络强度熵同时在t=13时达到1和降为0,即I(13)=1,G(13)=0,URTN的结构抗毁性和功能抗毁性同时在t=13时失效。由此可见,在URTN的级联失效过程中,结构抗毁性与功能抗毁性的演化规律相似,且同时失效。
|
| 图 12 不同轨道站点不同R下的URTN的网络强度熵演化规律 |
综上所述,险性扰动不会引发URTN级联失效,此时,URTN具有较好的结构抗毁性和功能抗毁性,而随着扰动程度增加(一般扰动、较大扰动、重大扰动、特别重大扰动),URTN的结构抗毁性和功能抗毁性的失效时间缩短,在受到重大扰动和特别重大扰动后,URTN的级联失效抗毁性演化规律相同。因此,应当重点防范URTN中的突发扰动,保障城市轨道交通的有序运营。
5.4.2 客流强度对城市轨道交通网络抗毁性的影响通过分析不同客流强度下,轨道站点在受到突发扰动后,URTN的结构抗毁性和功能抗毁性的演化规律,可进一步剖析轨道站点的客流强度对URTN抗毁性的影响机理。
基于CML模型中轨道站点间的相互作用关系,同一轨道站点的客流强度越大,初始状态值越大,受到突发扰动后出现故障,进而引发URTN级联失效的可能性越大。选取61号大雁塔站进行实例验证。设定一般扰动R=2,相邻轨道站点间的耦合系数ε=0.4,初始状态值分别为x61(0)=0.4、x61(0)=0.6、x61(0)=0.8,发现URTN的故障节点比达到1的时间排序为:t(x61(0)=0.8) < t(x61(0)=0.6) < t(x61(0)=0.4),即轨道站点的初始状态值越大,引发URTN级联失效的时间越短。因此,非均衡大客流冲击下,客流强度大小与URTN的抗毁性水平呈负相关,即客流强度大的轨道站点受突发扰动后,更易引发URTN级联失效,此时,URTN的抗毁性水平更弱。
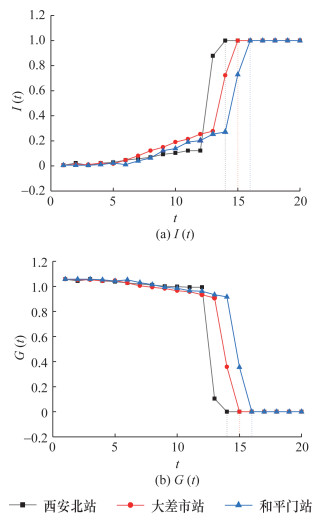
针对不同客流强度的轨道站点,选取早高峰时段非均衡大客流下,客流强度最大的站点西安北站(S43=7 010人次/h)、客流强度较大的站点大差市站(S80=4 611人次/h)、客流强度一般的站点和平门站(S81=1 702人次/h)为代表站点,探究客流强度对URTN抗毁性的影响机理。当一般扰动R=2,相邻轨道站点间的耦合系数ε=0.4时,URTN的故障节点比和网络强度熵的演化规律如图 13所示。
|
| 图 13 不同客流强度下不同轨道站点的故障节点比和网络强度熵演化规律 |
由图 13a可知,在同一耦合系数ε下,当受到的突发扰动R相同时,西安北站、大差市站、和平门站的故障节点比分别在t西安北=14、t大差市=15、t和平门=16时达到1,此时,URTN的结构抗毁性水平失效。因此,相同的突发扰动和耦合系数下,客流强度越大的轨道站点引发的级联失效传播越快,URTN的结构抗毁性水平越低、失效时间越短。当t≤12时,轨道交通处于级联失效初始阶段,故障站点数较少,突发扰动R仅传播至故障站点的相邻轨道站点,传播速度较慢。当t>12时,突发扰动传播速度加快,URTN中的轨道站点加速损毁,故障节点比迅速达到1。由此可见,URTN级联失效的传播需要一定时间,轨道交通管理部门应高度重视URTN的级联失效初始阶段,采取相应客流协同措施,最小化事故后果。同时,从图 13b可知:当t≤12时,网络强度熵变化较小,说明此时的URTN具有较好的功能抗毁性;当t>12时,网络强度熵迅速下降,说明此时的URTN的客运服务水平降低,URTN的功能抗毁性减弱,直至失效。
综上所述,耦合系数或突发扰动越大,URTN级联失效的传播规模越大,且传播速度越快,URTN的结构抗毁性和功能抗毁性失效时间越短;对于客流强度越大的轨道站点来说,受到突发扰动后,级联失效的传播速度越快,URTN的结构抗毁性和功能抗毁性失效时间越短。因此,通过降低URTN轨道站点间的耦合系数,重点防范轨道交通网络的突发扰动,协调控制轨道站点的客流强度,可有效减小URTN级联失效的故障传播速度和规模,提高URTN的结构抗毁性和功能抗毁性,保障城市轨道交通的有序运营。同时,URTN的级联失效传播需要一定时间,轨道交通管理部门应高度重视URTN的级联失效初期,采取相应客流协同措施,最小化事故后果。
6 结论本文基于非均衡大客流场景构建客流加权的URTN,通过设置轨道站点客流饱和程度为初始状态值改进CML模型,探究非均衡大客流冲击下,城市轨道交通网络结构抗毁性和功能抗毁性的影响因素及动态演化规律,得出如下主要结论。
1) 在URTN的级联失效过程中,结构抗毁性和功能抗毁性演化规律相似,同时变化,同时失效。在异质性关键站点中,节点介数大的轨道站点和客流强度大的轨道站点在受到突发扰动后,URTN的结构抗毁性水平和功能抗毁性水平更低。
2) URTN级联失效存在耦合系数临界值和突发扰动临界值。当ε或R小于临界值时,任意时间内均不会引发URTN级联失效,URTN具有较好的结构抗毁性和功能抗毁性;当ε和R大于临界值时,URTN的结构抗毁性和功能抗毁性水平失效的时间随ε和R的增大而缩短。同时,站点客流强度与URTN抗毁性水平呈负相关,客流强度大的轨道站点受扰动后更易引发URTN级联失效现象。
受数据可获性限制,本文在构建URTN抗毁性模型时仅考虑拓扑结构因素和客流强度因素对URTN抗毁性的影响,后续将在该模型的基础上,进一步研究URTN级联失效过程中,轨道交通应急公交接驳对URTN抗毁性的影响,深入探索级联失效过程中客流转移方式组合下的抗毁性动态演化规律。
| [1] |
HÖRCHER D, GRAHAM D J. Demand imbalances and multi-period public transport supply[J]. Transportation Research Part B: Methodological, 2018, 108: 106-126. DOI:10.1016/j.trb.2017.12.009 |
| [2] |
李锴, 何永锋, 吴纬, 等. 面向级联失效的复杂层次网络可靠性[J]. 华中科技大学学报(自然科学版), 2018, 46(9): 45-51. LI K, HE Y F, WU W, et al. Reliability of complex hierarchical network for cascading failure[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(9): 45-51. (in Chinese) |
| [3] |
马敏, 胡大伟, 刘杰, 等. 基于客流加权的城市轨道交通网络抗毁性分析[J]. 中国安全科学学报, 2022, 32(12): 141-149. MA M, HU D W, LIU J, et al. Invulnerability analysis of urban rail transit network based on weighted passenger flow[J]. China Safety Science Journal, 2022, 32(12): 141-149. (in Chinese) |
| [4] |
朱文金, 王罗昊佶, 蔡志强, 等. 考虑级联失效的可重构网络抗毁性研究[J]. 西北工业大学学报, 2021, 39(4): 839-846. ZHU W J, WANG L H J, CAI Z Q, et al. Resilience analysis for reconfigurable network with cascading failures[J]. Journal of Northwestern Polytechnical University, 2021, 39(4): 839-846. (in Chinese) |
| [5] |
XU J Q, HUANG H N, CHENG Y Q, et al. Vulnerability assessment of freeway network considering the probabilities and consequences from a perspective based on network cascade failure[J]. PLoS One, 2022, 17(3): e0265260. DOI:10.1371/journal.pone.0265260 |
| [6] |
杨景峰, 朱大鹏, 赵瑞琳. 城轨网络站点重要度评估与级联失效抗毁性分析[J]. 中国安全科学学报, 2022, 32(8): 161-167. YANG J F, ZHU D P, ZHAO R L. Evaluation of station importance and cascading failure resistance analysis of urban rail transit network[J]. China Safety Science Journal, 2022, 32(8): 161-167. (in Chinese) |
| [7] |
马书红, 武亚俊, 陈西芳. 城市群多模式交通网络结构韧性分析: 以关中平原城市群为例[J]. 清华大学学报(自然科学版), 2022, 62(7): 1228-1235. MA S H, WU Y J, CHEN X F. Structural resilience of multimodal transportation networks in urban agglomerations: A case study of the Guanzhong Plain urban agglomeration network[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(7): 1228-1235. (in Chinese) |
| [8] |
WU S J, ZHU Y, LI N, et al. Urban rail transit system network reliability analysis based on a coupled map lattice model[J]. Journal of Advanced Transportation, 2021, 2021: 5548956. |
| [9] |
王永岗, 王龙健, 刘志岗, 等. 多模式复合交通网脆弱性测度[J]. 交通运输工程学报, 2023, 23(1): 195-207. WANG Y G, WANG L J, LIU Z G, et al. Vulnerability metrics of multimodal composite transportation network[J]. Journal of Traffic and Transportation Engineering, 2023, 23(1): 195-207. (in Chinese) |
| [10] |
王秋玲, 朱璋元, 陈红, 等. 基于CML的级联失效下异质多层交通网络节点抵抗特性研究[J]. 中国公路学报, 2022, 35(1): 263-274. WANG Q L, ZHU Z Y, CHEN H, et al. Node resistance characteristic of heterogeneous multi-layer transportation networks under cascading failure based on coupled map lattice[J]. China Journal of Highway and Transport, 2022, 35(1): 263-274. (in Chinese) |
| [11] |
李成兵, 魏磊, 卢天伟, 等. 城市群交通网络抗毁性仿真研究[J]. 系统仿真学报, 2018, 30(2): 489-496. LI C B, WEI L, LU T W, et al. Invulnerability simulation analysis of compound traffic network in urban agglomeration[J]. Journal of System Simulation, 2018, 30(2): 489-496. (in Chinese) |
| [12] |
LU Q C, ZHANG L, XU P C, et al. Modeling network vulnerability of urban rail transit under cascading failures: A coupled map lattices approach[J]. Reliability Engineering & System Safety, 2022, 221: 108320. |
| [13] |
路庆昌, 刘鹏, 徐标, 等. 运营事件下基于韧性的地铁网络保护决策优化[J]. 交通运输工程学报, 2023, 23(3): 209-220. LU Q C, LIU P, XU B, et al. Resilience-based protection decision optimization for metro network under operational incidents[J]. Journal of Traffic and Transportation Engineering, 2023, 23(3): 209-220. (in Chinese) |
| [14] |
HUANG W C, ZHOU B W, YU Y C, et al. Using the disaster spreading theory to analyze the cascading failure of urban rail transit network[J]. Reliability Engineering & System Safety, 2021, 215: 107825. |
| [15] |
冯树民, 陈勇, 辛梦薇. 突发大客流下地铁协调限流优化模型[J]. 哈尔滨工业大学学报, 2019, 51(2): 179-185. FENG S M, CHEN Y, XIN M W. Coordination passenger flow control model for metro under sudden large passenger flow[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 179-185. (in Chinese) |
| [16] |
潘恒彦, 张文会, 胡宝雨, 等. 城市公交-地铁加权复合网络构建及鲁棒性分析[J]. 吉林大学学报(工学版), 2022, 52(11): 2582-2591. PAN H Y, ZHANG W H, HU B Y, et al. Construction and robustness analysis of urban weighted subway-bus composite network[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(11): 2582-2591. (in Chinese) |
| [17] |
冯霞, 贾宏璨. 考虑节点失效和边失效的航空网络鲁棒性[J]. 北京交通大学学报, 2021, 45(5): 84-92. FENG X, JIA H C. Aviation network robustness considering node failure and edge failure[J]. Journal of Beijing Jiaotong University, 2021, 45(5): 84-92. (in Chinese) |
| [18] |
刘朝阳, 吕永波, 刘步实, 等. 城市轨道交通运输网络级联失效抗毁性研究[J]. 交通运输系统工程与信息, 2018, 18(5): 82-87. LIU Z Y, Lü Y B, LIU B S, et al. Cascading failure resistance of urban rail transit network[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(5): 82-87. (in Chinese) |
| [19] |
李子浩, 田向亮, 黎忠文, 等. 基于客流规律的地铁车站客流风险分析[J]. 清华大学学报(自然科学版), 2019, 59(10): 854-860. LI Z H, TIAN X L, LI Z W, et al. Risk analysis of metro station passenger flow based on passenger flow patterns[J]. Journal of Tsinghua University (Science and Technology), 2019, 59(10): 854-860. (in Chinese) |
| [20] |
SUN J, YAO J J, WANG M X. Subway passenger flow analysis and management optimization model based on AFC data[J]. Journal of Intelligent & Fuzzy Systems, 2021, 41(4): 4773-4783. |
| [21] |
MA Z L, LIU J, CHIEN S I J, et al. Identifying critical stations affecting vulnerability of a metro network considering passenger flow and cascading failure: Case of Xi'an Metro in China[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2023, 9(2): 04023014. |
| [22] |
SHEN Y, REN G, RAN B. Analysis of cascading failure induced by load fluctuation and robust station capacity assignment for metros[J]. Transportmetrica A: Transport Science, 2022, 18(3): 1401-1419. |
| [23] |
ZHANG J H, WANG Z Q, WANG S L, et al. Vulnerability assessments of weighted urban rail transit networks with integrated coupled map lattices[J]. Reliability Engineering & System Safety, 2021, 214: 107707. |
| [24] |
SUN L S, HUANG Y C, CHEN Y Y, et al. Vulnerability assessment of urban rail transit based on multi-static weighted method in Beijing, China[J]. Transportation Research Part A: Policy and Practice, 2018, 108: 12-24. |
| [25] |
HASSAN R, YOSRI A, EZZELDIN M, et al. Robustness quantification of transit infrastructure under systemic risks: A hybrid network-analytics approach for resilience planning[J]. Journal of Transportation Engineering, Part A: Systems, 2022, 148(10): 04022089. |
| [26] |
中华人民共和国中央人民政府. 国务院办公厅关于印发国家城市轨道交通运营突发事件应急预案的通知[P]. (2015-05-14) [P]. https://www.gov.cn/zhengce/zhengceku/2015-05/14/content_9751.htm. Central Government of the People's Republic of China. Notice of The General Office of the State Council on printing and distributing the national emergency response plan for urban rail transit operations [P]. (2015-05-14) [P]. https://www.gov.cn/zhengce/zhengceku/2015-05/14/content_9751.htm. (in Chinese) |
| [27] |
李颖薇, 冯套柱. 基于fsQCA(模糊集定性比较分析)的城市轨道交通运营安全风险研究[J]. 城市轨道交通研究, 2023, 26(8): 180-183, 191. LI Y W, FENG T Z. Study on urban rail transit operational safety risks based on fsQCA[J]. Urban Mass Transit, 2023, 26(8): 180-183, 191. (in Chinese) |
| [28] |
胡启洲, 张晓亮, 吴翊恺, 等. 车路协同下高速公路运行态势监测方法[J]. 东南大学学报(自然科学版), 2020, 50(6): 1143-1147. HU Q Z, ZHANG X L, WU Y K, et al. Monitoring method for traffic situation of highway under vehicle-infrastructure cooperation[J]. Journal of Southeast University (Natural Science Edition), 2020, 50(6): 1143-1147. (in Chinese) |
| [29] |
SHEN Y, REN G, RAN B. Cascading failure analysis and robustness optimization of metro networks based on coupled map lattices: A case study of Nanjing, China[J]. Transportation, 2021, 48(2): 537-553. |
| [30] |
杨阳, 孙利民. 基于FPP-Grey的地铁车站火灾安全灰色聚类评价[J]. 安全与环境工程, 2019, 26(2): 99-104. YANG Y, SUN L M. Grey clustering evaluation of fire safety of subway station based on FPP-Grey[J]. Safety and Environmental Engineering, 2019, 26(2): 99-104. (in Chinese) |
| [31] |
陈长坤, 何凡, 赵冬月, 等. 基于系统机能曲线的城市道路公共交通系统韧性评估方法[J]. 清华大学学报(自然科学版), 2022, 62(6): 1016-1022. CHEN C K, HE F, ZHAO D Y, et al. Urban public transport system resilience evaluation based on a system function curve[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(6): 1016-1022. (in Chinese) |
| [32] |
熊志华, 姚智胜. 轨道交通网络级联失效影响范围研究[J]. 交通运输系统工程与信息, 2020, 20(1): 12-18. XIONG Z H, YAO Z S. Influence scope of cascading failure on rail transit system[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(1): 12-18. (in Chinese) |
| [33] |
ZHANG L, XU M, WANG S A. Quantifying bus route service disruptions under interdependent cascading failures of a multimodal public transit system based on an improved coupled map lattice model[J]. Reliability Engineering & System Safety, 2023, 235: 109250. |
| [34] |
黄爱玲, 徐笑涵, 关伟, 等. 基于加权耦合映像格子的地铁网络稳定性演化研究[J]. 交通运输系统工程与信息, 2021, 21(3): 140-149. HUANG A L, XU X H, GUAN W, et al. Evolution of metro network stability based on weighted coupled map lattice[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(3): 140-149. (in Chinese) |
| [35] |
ALBERT R, JEONG H, BARABÁSI A L. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6794): 378-382. |



