 PDF(12497 KB)
PDF(12497 KB)


Nonlinear mechanical response of prestressed segmented steel-concrete towers
Mingjin LIAO, Kezheng FAN, Yu XU
Journal of Tsinghua University(Science and Technology) ›› 2025, Vol. 65 ›› Issue (8) : 1583-1595.
 PDF(12497 KB)
PDF(12497 KB)
 PDF(12497 KB)
PDF(12497 KB)
Nonlinear mechanical response of prestressed segmented steel-concrete towers
Objective: The primary goal of this study is to address the rising costs linked to the production, transportation, and construction of traditional conical wind turbine towers with increasing wind turbine sizes. Therefore, a novel design for an internally prestressed segmented steel-concrete tower structure is proposed, aiming to improve static performance and structural integrity, reducing material usage, and improving the overall efficiency of the wind turbine tower structure. Methods: Detailed finite element models of the traditional conical steel and new prestressed segmented steel-concrete towers are developed using the ABAQUS platform. These models accurately reflect the geometric complexity and material properties of the structures. The material properties of steel and concrete are defined based on their mechanical characteristics. For concrete, a plastic damage model is utilized to capture its inelastic behavior, whereas steel is modeled using a bilinear stress-strain relationship to represent its yielding and hardening behavior. The models are tested under realistic boundary conditions that simulate the fixed bases of the towers. The loading conditions include the dead load of the tower structure, the weight of the turbine components, and the dynamic loads from the 3-D turbulent wind field during shutdown. Wind loads are calculated using GH-Bladed software simulations specific to the wind turbine model. Prestressing is applied to the new tower model using two methods: temperature reduction and equivalent load. The temperature reduction method simulates prestress by cooling the tendons, whereas the equivalent load method applies an external force equivalent to the prestress effect. Moreover, static and dynamic analyses are performed on the models. Static analyses evaluate stress distribution, displacement, and the linear and nonlinear buckling performances of the tower. Dynamic analyses examine modal characteristics, including natural frequencies and mode shapes. Parametric studies are constructed to understand how various design parameters, including prestress levels, tower wall thickness, tower radius, and concrete strength, affect structural performance. The results of these studies provide insights into the sensitivity of these parameters to the structure. Nonlinear analyses are conducted to account for material and geometric nonlinearities in the structure, which are crucial for accurately predicting the ultimate load-carrying capacity and postbuckling behavior of the towers. The finite element models are validated against experimental data and other numerical studies from the literature, ensuring the simulation results are reliable and accurate. Results: The static performance of the new tower structure is considerably improved without prestressing. The maximum equivalent stress, tower top displacement, and steel usage drop by 10.24%, 14.89%, and 9.51%, respectively. Furthermore, the first natural frequency increases by 7.5% compared to the traditional conical tower. When prestressing is applied, the maximum equivalent stress of the new tower structure and tower top displacement drop by 0.36% and 6%, and the first natural frequency rises by up to 7.6% compared to the nonprestressed state. Compared to the new tower without prestressing, the prestressed tower exhibits a 9.27% enhancement in its linear buckling load; during nonlinear buckling analysis, the load proportionality factor rises by roughly 4.6%, 4.1%, and 4.8% when considering only material nonlinearity, considering both material and geometric nonlinearity, and considering material and geometric nonlinearity along with initial defects. Without prestressing, the ultimate bending capacity of the new tower is 1.15 times that of the traditional conical steel tower. After adding prestressed tendons, this capacity increases by another 6.5%. The weak points near buckling in the new and traditional conical towers are located in section 6 (approximately halfway up the tower). The new tower without prestressing shows better buckling performance than the traditional tower. When prestressing is applied, the ultimate buckling load is minimally affected by the prestress level, with overall buckling performance mainly constrained by the buckling behavior of the thin-walled segments, as seen in the segmented steel tower. Conclusions: The new prestressed segmented steel-concrete tower structure offers remarkable advantages over traditional conical steel towers in terms of static performance, modal characteristics, and buckling resistance. The use of prestressing enhances structural efficiency and optimizes material utilization. This comprehensive analysis provides a scientific foundation for the engineering application of the new tower structure, indicating it as a viable and promising solution for next-generation wind turbine towers.
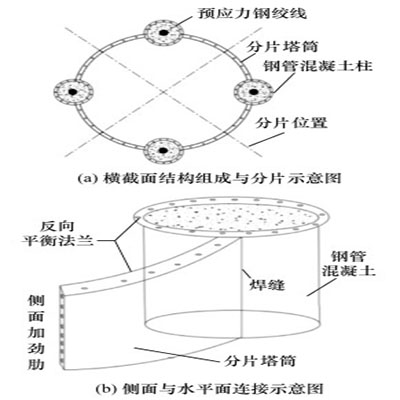
prestress / steel-concrete hybrid tower / nonlinearity / mechanical response / buckling performance
| 1 |
陶涛, 龙凯, 白欣鉴, 等. 风电机组高柔塔二阶涡激振动特性研究[J]. 太阳能学报, 2022, 43 (2): 498- 503.
|
| 2 |
王佼姣, 施刚, 石永久, 等. 考虑不同边界约束条件下的风电机塔架固有频率分析[J]. 特种结构, 2011, 28 (5): 5-8, 108.
|
| 3 |
|
| 4 |
葛文澎, 苗得胜, 吴迪, 等. 风力发电机组液态阻尼器减振设计研究[J]. 可再生能源, 2022, 40 (4): 499- 505.
|
| 5 |
|
| 6 |
李杨, 兰涌森, 李强, 等. 风力机塔架结构振动控制研究及方法综述[J]. 船舶工程, 2020, 42 (S2): 248- 253.
|
| 7 |
|
| 8 |
BRUGHUIS F J. Advanced tower solutions for large wind turbines and extreme tower heights[C]//Proceedings of the European Wind Energy Conference & Exhibition. Madrid, Spain, 2003.
|
| 9 |
|
| 10 |
|
| 11 |
张志川. 有限元计算中预应力等效模拟方法研究[J]. 人民黄河, 2020, 42 (S1): 122-125, 127.
|
| 12 |
王长军, 李鹤飞, 胡邵凯, 等. 预应力钢-混凝土超高风电塔架数值模型及计算分析[J]. 建筑结构, 2019, 49 (S1): 955- 958.
|
| 13 |
张向荣. 钢管混凝土结构在高层建筑中的应用现状及发展[J]. 中外建筑, 2007 (7): 67- 68.
|
| 14 |
潘方树, 王法武, 柯世堂, 等. 考虑缺陷的大型风力机塔筒屈曲分析与稳定性设计[J]. 太阳能学报, 2017, 38 (10): 2659- 2664.
|
| 15 |
European Commission. Eurocode 3: Design of steel structures-Part 1-1: General rules and rules for buildings: CEN-EN 1993-1-1[S]. Brussels, Belgium: CEN, 2005.
|
| 16 |
European Commission. Eurocode 4: Design of composite steel and concrete structure-Part 1-1: General rules and rules for buildings: BS EN 1994-1-1[S]. Brussels, Belgium: CEN, 2004.
|
| 17 |
徐悟, 于清, 尧国皇. 初应力对钢管混凝土叠合柱轴压性能影响[J]. 清华大学学报(自然科学版), 2014, 54 (5): 556- 562.
|
| 18 |
韩林海. 钢管混凝土结构: 理论与实践[M]. 2版. 北京: 科学出版社, 2007.
|
| 19 |
黄斌洁. 圆中空夹层钢管混凝土柱在扭转受力状态下的力学性能研究[D]. 南昌: 华东交通大学, 2012.
HUANG B J. Research on behavior of concrete filled double-skin steel tubular columns subjected to pure torsion[D]. Nanchang: East China Jiaotong University, 2012. (in Chinese)
|
| 20 |
中华人民共和国住房和城乡建设部, 国家市场监督管理总局. 高耸结构设计规范: GB 50135-2019[S]. 北京: 中国计划出版社, 2019.
Ministry of Housing and Urban-Rural Development of the People's Republic of China, State Aministration for Market Regulation. Standard for design of high-rising structures: GB 50135-2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
|
| 21 |
张伟东, 王宇展. 框排架结构强震下静力弹塑性分析[J]. 城市建设理论研究(电子版), 2023 (4): 128- 130.
|
| 22 |
侯晓萌, 王英, 郑文忠. 预应力等效荷载作用下内力计算简化方法[J]. 低温建筑技术, 2004 (2): 29- 30.
|
| 23 |
何琳, 王家林. 模拟有效预应力的等效荷载-实体力筋降温法[J]. 公路交通科技, 2015, 32 (11): 75- 80.
|
| 24 |
|
| 25 |
|
| 26 |
周凯明, 王法武, 程晔, 等. 考虑材料塑性损伤的风力机塔筒屈曲稳定性分析[J]. 建筑钢结构进展, 2023, 25 (5): 63- 69.
|
| 27 |
白璐涵. 预应力支撑式圆中空夹层钢管混凝土柱轴压力学性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
BAI L H. Behavior of prestressed stayed circular concrete filled double skin steel tubular columns under axial compression load[D]. Harbin: Harbin Institute of Technology, 2020. (in Chinese)
|
| 28 |
任洪鹏. 预应力钢筋混凝土风力发电塔架的静力及地震响应分析[D]. 天津: 天津大学, 2011.
REN H P. The static and seismic analysis of prestressed reinforced concrete wind-turbine tower[D]. Tianjin: Tianjin University, 2011. (in Chinese)
|
| 29 |
余智, 张凤亮, 熊海贝. 基于线性累计损伤理论的预应力混凝土风电塔架疲劳可靠性及剩余寿命研究[J]. 武汉大学学报(工学版), 2016, 49 (5): 756- 762.
|
/
| 〈 |
|
〉 |